Материал для повторения в 10 классе
перед изучением темы функции на уроках алгебры и начал анализа или элективного курса «Избранные вопросы математики».
Тема «Функции»
Продолжи!
Функция – это…
Способы задания функции называются…
Функцию можно задать с помощью…
Независимая переменная называется…
Зависимая переменная называется…
Множество независимых переменных называется…
Множество зависимых переменных называется…
Область определения функции обозначаются…
Область значений функции обозначается…
Графиком функции называется множество всех точек координатной плоскости, абциссы которых равны…, а ординаты которых равны…
Возрастающая функция – это такая функция, при которой…
Убывающая функция – это такая функция, при которой…
Четная функция, если для неё выполняется равенство…
Нечетная функция, если для неё выполняется равенство…
Если для функции не выполняются оба равенства, то функция… График четной функции симметричен относительно…
График нечетной функции симметричен относительно…
Графиком линейной функции y = kx+b является…
Графиком прямой пропорциональности y = kx является…
Графиком постоянной функции y = b является…
Графиком квадратичной функции у =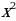 является…
является…
Графиком кубической функции у =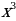 является…
является…
Графиком обратной пропорциональности y = 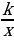 является…
является…
Графиком квадратичной функции у =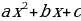 является…
является…
Графиком функции y = 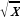 является…
является…
Функция – возрастающая, если для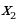
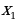 выполняется…
выполняется…
Функция – убывающая, если для 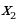
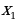 выполняется…
выполняется…
Нули функции – это значения аргумента, при которых…
Нули функции на координатной плоскости – это точки пересечения графика функции с осью x.
Промежутки знакопостоянства – это промежутки, в которых функция…
Промежутки знакопостоянства на координатной плоскости – это части графика между нулями функции, расположенные…
Наибольшее значение функции на определённом промежутке – это …
Наибольшее значение функции на координатной плоскости – это точка перехода между промежутками…
Наименьшее значение функции на определённом промежутке – это …
Наименьшее значение функции на координатной плоскости – это точка перехода между промежутками…
Алгоритм построения квадратичной функции у =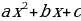 :
:
Построение квадратичной функции у = a 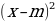 + n:
+ n:
План исследования функции f (х):
Рекомендации для учащихся.
Если ты затрудняешься с ответами на поставленные вопросы, то воспользуйся справочными материалами.
Повторив материал попробуй снова закончить фразы.
Если всё еще затрудняешься, то ищи ответы на вопросы в справочных материалах.
Постарайся запомнить ответы.
Сохрани справочные материалы.
Справочные материалы по теме «Функции»
Функция – это зависимость у от х, при которой каждому значению х из области определения соответствует единственное значение у из области значений.
Способы задания функции: аналитический, графический, табличный.
Функцию можно задать с помощью формулы, графика, таблицы.
Независимая переменная называется аргумент или х.
Зависимая переменная называется функция или у.
Множество независимых переменных называется областью определения функции и обозначается Д(у).
Множество зависимых переменных называется областью значения функции и обозначается Е(у).
Графиком функции называется множество всех точек координатной плоскости, абциссы которых равны значениям аргумента, а ординаты которых равны значениям функции.
Возрастающая функция – это такая функция, при которой,
если х ↗, то и у ↗.
Убывающая функция – это такая функция, при которой,
если х ↗, то у ↘.
Четная функция, если для неё выполняется равенство:
f (- х ) = f ( х )
Нечетная функция, если для неё выполняется равенство:
f (- х ) = - f ( х )
Если для функции не выполняются оба равенства, то функция не является ни четной ни нечетной.
График четной функции симметричен относительно оси у, а график нечетной функции симметричен относительно начала координат.
Графиком линейной функции y = kx+b является прямая, строится по двум точкам. При к 0, прямая проходит в 1 и 3 координатных четвертях, а при к
0, прямая проходит в 1 и 3 координатных четвертях, а при к  0, прямая проходит во 2 и 4 координатных четвертях.
0, прямая проходит во 2 и 4 координатных четвертях.
Графиком прямой пропорциональности y = kx является прямая, проходящая через начало координат, строится по двум точкам, одна из которых (0; 0). При к 0, прямая проходит в 1 и 3 координатных четвертях, а при к
0, прямая проходит в 1 и 3 координатных четвертях, а при к  0, прямая проходит во 2 и 4 координатных четвертях.
0, прямая проходит во 2 и 4 координатных четвертях.
Графиком постоянной функции y = b является прямая, параллельная оси x, строится параллельно оси х, через точку (0; b).
Графиком квадратичной функции у =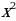 является парабола, вершина которой – начало координат, расположена в 1 и 2 координатных четвертях, строится по точкам: (0; 0), (1; 1), (-1; 1), (2; 4), (-2; 4), (3;9), (-3;9) .
является парабола, вершина которой – начало координат, расположена в 1 и 2 координатных четвертях, строится по точкам: (0; 0), (1; 1), (-1; 1), (2; 4), (-2; 4), (3;9), (-3;9) .
Графиком кубической функции у =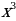 является кубическая парабола, вершина которой – начало координат, расположена в 1 и 3 координатных четвертях, строится по точкам: (0; 0), (1; 1), (-1; -1), (2; 8), (-2; -8).
является кубическая парабола, вершина которой – начало координат, расположена в 1 и 3 координатных четвертях, строится по точкам: (0; 0), (1; 1), (-1; -1), (2; 8), (-2; -8).
Графиком обратной пропорциональности y = 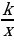 является гипербола. При к
является гипербола. При к 0, график проходит в 1 и 3 координатных четвертях, а при к
0, график проходит в 1 и 3 координатных четвертях, а при к  0, график проходит во 2 и 4 координатных четвертях.
0, график проходит во 2 и 4 координатных четвертях.
Графиком функции y = 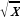 является ветвь параболы, расположена в 1 координатной четверти, строится по точкам: (0; 0), (1; 1), (4; 2), (9; 3), (16; 4).
является ветвь параболы, расположена в 1 координатной четверти, строится по точкам: (0; 0), (1; 1), (4; 2), (9; 3), (16; 4).
Графиком квадратичной функции у =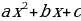 является парабола.
является парабола.
Алгоритм построения квадратичной функции
у =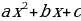 :
:
Определить направление ветвей:
если 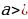 0, то ветви параболы направлены вверх;
0, то ветви параболы направлены вверх;
если 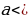 0, то ветви параболы направлены вниз.
0, то ветви параболы направлены вниз.
Найти вершину параболы по формулам:
x = 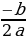 ; y =
; y = 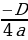 или х =
или х = 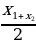
Найти нули функции, то есть решить квадратное уравнение: 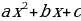 = 0.
= 0.
Найти точки пересечения с осью у, то есть точка (0; 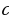 )
)
При необходимости найти другие точки.
Построение квадратичной функции у = a 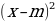 + n:
+ n:
Определить направление ветвей:
если 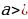 0, то ветви параболы направлены вверх;
0, то ветви параболы направлены вверх;
если 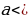 0, то ветви параболы направлены вниз.
0, то ветви параболы направлены вниз.
Вершина параболы (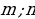 ).
).
Построить ещё несколько точек, принадлежащих параболе.
Осью симметрии параболы служит прямая х =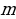 , параллельная оси у.
, параллельная оси у.
График функции у = a 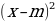 + n можно построить из графика функции
+ n можно построить из графика функции
у = aх, путём сдвига вдоль оси х на 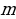 единиц и вдоль оси у на n единиц.
единиц и вдоль оси у на n единиц.
Функция – возрастающая, если для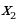
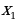 выполняется
выполняется
f (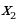 ) f (
) f (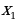 )
)
Функция – убывающая, если для 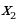
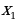 выполняется
выполняется
f (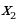 )
) 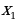 )
)
Нули функции – это значения аргумента, при которых функция обращается в нуль, y = 0 или f (x) = 0.
Нули функции на координатной плоскости – это точки пересечения графика функции с осью x.
Промежутки знакопостоянства – это промежутки, в которых функция сохраняет знак, y  0, y
0, y  0 или f (x)
0 или f (x)  0, f (x)
0, f (x)  0.
0.
Промежутки знакопостоянства на координатной плоскости – это части графика между нулями функции, расположенные выше оси x или ниже оси x.
Наибольшее значение функции на определённом промежутке – это самое большое значение y, а наименьшее значение функции на определённом промежутке – это самое маленькое значение y.
Наибольшее значение функции на координатной плоскости – это точка перехода между промежутками возрастания и убывания функции:
f (х) ↗ и f (х) ↘.
Наименьшее значение функции на координатной плоскости – это точка перехода между промежутками убывания и возрастания функции:
f ( х) ↘ и f ( х ) ↗ .
План исследования функции f (х)
Область определения. Д(f) =…
Область значений. Е(f) =…
Промежутки возрастания и убывания:
f ( х ) ↗ , при х 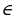 … f ( х ) ↘ , при х
… f ( х ) ↘ , при х 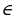 ...
...
Промежутки знакопостоянства:
f ( x )  0, при х
0, при х 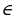 … f ( x )
… f ( x )  0, при х
0, при х 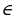 …
…
Нули функции.
Четность, нечетность функции.
Наибольшее и наименьшее значение функции.
Учитель Дудченко С. В.







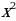 является…
является… 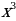 является…
является… 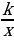 является…
является… 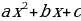 является…
является… 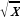 является…
является… 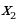
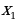 выполняется…
выполняется… 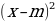 + n:
+ n: 0, прямая проходит в 1 и 3 координатных четвертях, а при к
0, прямая проходит в 1 и 3 координатных четвертях, а при к 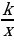 является гипербола. При к
является гипербола. При к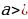 0, то ветви параболы направлены вверх;
0, то ветви параболы направлены вверх;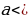 0, то ветви параболы направлены вниз.
0, то ветви параболы направлены вниз.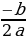 ; y =
; y = 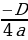 или х =
или х = 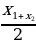
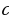 )
)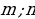 ).
).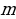 , параллельная оси у.
, параллельная оси у. … f ( х ) ↘ , при х
… f ( х ) ↘ , при х 









