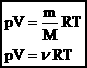Уравнение состояния идеального газа (уравнение Менделеева—Клапейрона). Изопроцессы
1. Уравнение состояния. 2. Уравнение Менделеева— Клапейрона. 3. Процессы в газах. 4. Изопроцессы. 5. Графики изопроцессов. 6. Распространенные ошибки.
Состояние данной массы газа полностью определено, если известны его давление, температура и объем. Эти неличины называют параметрами состояния газа. Уравнение, связывающее параметры состояния, называют уравнением состояния.
Для произвольной массы газа состояние газа описывается уравнением Менделеева—Клапейрона:
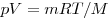 ,
,
где 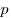 — давление,
— давление, 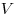 — объем,
— объем, 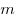 — массa,
— массa, 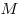 - молярная масса,
- молярная масса, 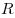 — универсальная газовая постоянная (
— универсальная газовая постоянная (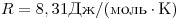 ). Физический смысл универсальной газовой постоянной в том, что она показывает, какую работу совершает один моль идеального газа при изобарном расширении при нагревании на 1 К.
). Физический смысл универсальной газовой постоянной в том, что она показывает, какую работу совершает один моль идеального газа при изобарном расширении при нагревании на 1 К.
Уравнение Менделеева—Клапейрона показывает, что возможно одновременное изменение трех параметров, характеризующих состояние идеального газа. Однако многие процессы в газах, происходящие в природе и осуществляемые в технике, можно рассматривать приближенно как процессы, в которых изменяются лишь два параметра. Особую роль в физике и технике играют три процесса: изотермический, изохорный и изобарный.
Изопроцессом называют процесс, происходящий с данной массой газа при одном постоянном параметре — температуре, давлении или объеме. Из уравнения состояния как частные случаи получаются законы для изопроцессов.
Изотермическим называют процесс, протекаю-щий при постоянной температуре: 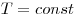 . Он описывается законом Бойля—Мариотта:
. Он описывается законом Бойля—Мариотта: 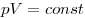 .
.
Изохорным называют процесс, протекающий при постоянном объеме: 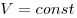 . Для него справедлив закон Шарля:
. Для него справедлив закон Шарля:  .
.
Изобарным называют процесс, протекающий при постоянном давлении. Уравнение этого процесса имеет вид 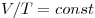 при
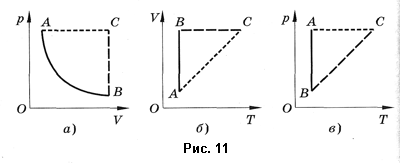
при 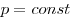 и называется законом Гей-Люссака. Все изопроцессы можно изобразить графически. На рисунке 11 представлены в различных координатах графики процессов: изотермического (изотерма АВ), изобарного (изобара АС) и изохорного (изохора ВС).
и называется законом Гей-Люссака. Все изопроцессы можно изобразить графически. На рисунке 11 представлены в различных координатах графики процессов: изотермического (изотерма АВ), изобарного (изобара АС) и изохорного (изохора ВС).
Реальные газы удовлетворяют уравнению состояния идеального газа при не слишком высоких давлениях (пока собственный объем молекул пренебрежимо мал по сравнению с объемом сосуда, в котором находится газ) и при не слишком низких температуpax (пока потенциальной энергией межмолекулярного взаимодействия можно пренебречь по сравнению с кинетической энергией теплового движения молекул), т. е. для реального газа это уравнение и его следствия являются хорошим приближением.
| Уравнение состояния идеального газа (уравнение Менделеева – Клапейрона). |
| Уравнением состояния называется уравнение, связывающее параметры физической системы и однозначно определяющее ее состояние. В 1834 г. французский физик Б. Клапейрон, работавший дли тельное время в Петербурге, вывел уравнение состояния идеального газа для постоянной массы газа. В 1874 г. Д. И. Менделеев вывел уравнение для произвольного числа молекул. | |
| В МКТ и термодинамике идеального газа макроскопическими параметрами являются: p, V, T, m. Мы знаем, что 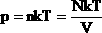 . Следовательно, . Следовательно, 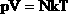 . Учитывая, что . Учитывая, что 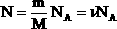 , получим: , получим: 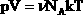 . . | |
| Произведение постоянных величин есть величина постоянная, следовательно: 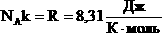 - универсальная газовая постоянная (универсальная, т.к. для всех газов одинаковая). - универсальная газовая постоянная (универсальная, т.к. для всех газов одинаковая). | 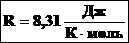
|
| Таким образом, имеем: 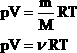 - уравнение состояния (уравнение Менделеева – Клапейрона). - уравнение состояния (уравнение Менделеева – Клапейрона).
| 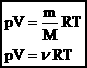
|
| Другие формы записи уравнения состояния идеального газа. |
| 1.Уравнение для 1 моля вещества. Если n=1 моль, то, обозначив объем одного моля Vм, получим: 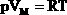 . . Для нормальных условий получим: 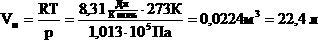 | 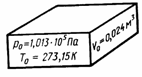
|
| 2. Запись уравнения через плотность:  - плотность зависит от температуры и давления! - плотность зависит от температуры и давления! | 
|
| 3. Уравнение Клапейрона. Часто необходимо исследовать ситуацию, когда меняется состояние газа при его неизменном количестве (m=const) и в отсутствие химических реакций (M=const). Это означает, что количество вещества n=const. Тогда:  | |
| Эта запись означает, что для данной массы данного газа справедливо равенство:  | |
| Для постоянной массы идеального газа отношение произведения давления на объем к абсолютной температуре в данном состоянии есть величина постоянная:  . . | 
|
| Газовые законы. |
| 1. Закон Авогадро. В равных объемах различных газов при одинаковых внешних условиях находится одинаковое число молекул (атомов). Условие: V1=V2=…=Vn; p1=p2=…=pn; T1=T2=…=Tn | |
| Доказательство: Следовательно, при одинаковых условиях (давление, объем, температура) число молекул не зависит от природы газа и одинаково. | |
| 2. Закон Дальтона. Давление смеси газов равно сумме парциальных (частных) давлений каждого газа. Доказать: p=p1+p2+…+pn Доказательство: | |
| 3. Закон Паскаля. Давление, производимое на жидкость или газ, передается во все стороны без изменения. |
|







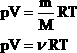 - уравнение состояния (уравнение Менделеева – Клапейрона).
- уравнение состояния (уравнение Менделеева – Клапейрона).