© 2016 4329 16


СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 18.05.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

МАТЕМАТИЧЕСКИЕ ТЕРМИНЫ В ЛИНГВИСТИКЕ
Математическая лингвистика – это отрасль языкознания, занимающаяся изучением возможностей применения математических методов к изучений и описанию языка.
Просмотр содержимого документа
«Математические термины Кон О.В.»
МИНИСТЕРСТВО ВЫСШЕГО И СРЕДНЕ-СПЕЦИАЛЬНОГО ОБРАЗОВАНИЯ РЕСПУБЛИКИ УЗБЕКИСТАН
ТАШКЕНТСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ НИЗАМИ
МАТЕМАТИЧЕСКИЕ ТЕРМИНЫ В ЛИНГВИСТИЧЕСКОМ АНАЛИЗЕ
МЕТОДИЧЕСКОЕ ПОСОБИЕ
ТАШКЕНТ 2010
СОДЕРЖАНИЕ
I. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ПРЕПОДАВАНИЯ ЛИНГВОМАТЕМА-
ТИЧЕСКИХ ДИСЦИПЛИН
1.1. Математические тенденции в системе филологического образования.
1.2. Формирование математической культуры студентов филологических отделений вузов.
1.3. Различия между естественным и математическим языками.
Содержание
1.Математические тенденции в гуманитарном образовании
2. Математизация лингвистических дисциплин
3. Особенности естественного языка в сравнении с математическим
4.Формирование математической компетенции лингвистов.
5. Множество лингвистических объектов.
6.Основные операции с лингвистическими множествами
7.Понятие функции в лингвистике.
8.Учет обратных функций при обучении языку и переводу.
9.Применение математических графов в лингвистике.
10.Лингвистическое моделирование.
1. Математические тенденции в гуманитарном образовании
Если проследить эволюцию человеческого знания, то станет очевидным, что оно давно и успешно математизируется. Однако заметна и обратная тенденция – методы гуманитарных наук проникают в те области знаний, которые традиционно считались негуманитарными. Данные процессы идут разными путями: математика, проникая в любую область знания, превращается в язык, на котором строятся модели, но сущность данной области от этого не меняется.
Становление гуманитарных наук по времени совпадает с историей математики. Развитие гуманитарных знаний и математики не было параллельным движением, оно неоднократно пересекалось: И.Ньютон, Б.Спиноза, Г.Лейбниц в своих исследованиях неоднократно апеллировали к математическим методам.
В ХХ веке ранее неустойчивый союз математики и гуманитарных наук укрепился настолько, что появилась насущная потребность учитывать его наличие в вузовском образовании. Во многом эта метаморфоза объясняется принципиальным изменением мнения о познавательном потенциале математики. Длительное время математику рассматривали только в технологическом ракурсе, в качестве инструментария. Эвристическая функция математики раскрылась на рубеже Х1Х и ХХ веков.
В гуманитарных науках значение математики огромно. Математика имеет дело с возможными мирами структур, упорядоченными совокупностями объектов. Любая гуманитарная наука изучает некоторую общность объектов, свойства и отношения, присущие им. Таким образом, математика раздвигает область своего применения и актуализирует ее. К исследовательскому аппарату гуманитарных наук подключаются огромнейшие резервы математики, накопленные ею за тысячелетия.
Математика решающим образом способствует установлению упорядочению гуманитарных структур. Она открывает нам структурные отношения объектов социального познания и предоставляет исключительно эффективный математический аппарат. Тот, кто не владеет математикой, не способен проникнуть в глубинные структурные отношения сложных динамически меняющихся объектов.
Начиная с древности, математику широко используют в социальной практике людей, например, в строительном, военном искусстве. И тем не менее включение математики в практическую социокультуру оставалось ограниченным. Оно становится по-настоящему эффективным только тогда, когда осуществляется математизация самосознания. Математизация гуманитарных наук способствует познанию, управлению, прогнозированию и профилактике кризисных явлений, которыми насыщена современная историческая ситуация.
Математизация гуманитарного образования ориентирована не только на обучение математическому мышлению, но и на развитие с помощью математики самого профессионального мышления гуманитариев. В соответствии с чем приоритетной задачей обучения математики в гуманитарных вузах становится не изучение основ математической науки как таковой, а обще интеллектуальное развитие – формирование у студентов мышления, необходимого для полноценного функционирования человека в современном обществе. Конкретные математические знания выступают базой организации полноценной в интеллектуальном и идейном отношении деятельности.
Гуманитарный потенциал математики раскрывается по следующим направлениям:
1.Математика изучает математические модели реальных процессов. Это позволит человеку, владеющему математическим языком, глубже проникнуть в суть реальных процессов, правильно ориентироваться в окружающей действительности.
2.Математика «ум в порядок приводит» (Ломоносов). Известно влияние математики на формирование мышления и личностных черт человека.
3.Человек, формулирующий математическое утверждение и приводящий математическое доказательство, оперирует не обыденной, а предметной речью, строящейся по определенным законам (краткость, четкость, лаконичность, минимизация и т.д.). Предметная речь оказывает существенное влияние и на развитие литературной речи.
4.Изучая математику, человек постоянно осознает свое развитие, «поумнение». Осознанность процесса обучения – один из краеугольных принципов теории развивающего обучения – обучение на достаточно высоком уровне трудности, быстрый тем обучения, приоритет теории, дифференцированный подход к учащимся плюс упомянутый выше принцип осознанности процесса обучения, то нетрудно убедиться, что обучение математике наиболее адекватно соответствует системе этих принципов, Именно поэтому в качестве основополагающего принципа формирования математической компетенции у гуманитариев на первый план выдвигается принцип приоритета развивающей функции в обучении.
2. Математизация лингвистических дисциплин.
В эпоху научно-технической революции математизация охватывает все сферы человеческой деятельности, в том числе и такие, казалось бы, чисто гуманитарные науки как языкознание, проникновение математических методов в лингвистику обусловлено двумя причинами.
Во-первых, развитие языковедческой теории и практики требует введения все более точных и объективных методов для анализа языка и текста. Одновременно использование математических приемов при систематизации, измерении и обобщении лингвистического материала в сочетании с качественной интерпретацией результатов позволяет языковедам глубже проникнуть в тайны построения языка и образования текста.
Во-вторых, все расширяющиеся связи языкознания с другими науками, например, с акустикой, физиологией высшей нервной деятельности, кибернетикой, вычислительной техникой, могут осуществляться только при использовании математического языка, обладающего высокой степенью общности и универсальности для различных отраслей знания. Особенно настойчиво математизируются языкознание в связи с использованием естественного языка в информационных и управленческих системах человек-машина- человек. В действующих системах машинного перевода автоматического аннотирования, человеко-машинного диалога всякое сообщение на естественном языке перекодируется в математическом языке компьютера. Применение математических методов в языкознании имеет своей целью заменить обычно диффузную, интуитивно сформулированную и не имеющую полного решения лингвистическую задачу одной или несколькими более простыми, логически сформулированными и имеющими алгоритмическое решение математическими задачами. Такое расчленение сложной лингвистической проблемы на более простые алгоритмизируемые задачи мы будем называть математической экспликацией лингвистического объекта или явления. Процедуру представления реальных объектов в виде математических можно назвать математической формализацией. В науках о неживой природе объекты моделируются довольно точно. Иная ситуация складывается в более сложных областях мира, особенно в объектах, изучаемых гуманитарными науками.
Математическая лингвистика. Математическая лингвистика использует метод абстрактно-семиотического моделирования явлений естественных языков и процессов их исследования. Центральными понятиями математической лингвистики являются понятия множества исходных символов (алфавит, словарь) и множества последовательностей (цепочек) символов заданного алфавита (множество словоформ, фраз). Эти основные понятия применяются на каждом уровне языка. Отношения между символами на заданном множестве и в цепочке аналогичны парадигматическим и синтагматическим отношениям, рассматриваемым в языкознании. Появление некоторого символа или последовательности символов на заданном мечте в цепочке называется их вхождение м в эту цепочку. Вхождения, удовлетворяющие специальным условиям, образуют систему составляющих данной цепочки. Графическое изображение системы составляющих во многих отношениях аналогично принятому в школьной грамматике изображению структуры предложения, Задавая разные типы отношений между символами в алфавите или в цепочке, сопоставляя допустимые и недопустимые цепочки и производя нужные разбиения исходного множества на подмножества, получают аналоги синтаксических отношений, классов слов, парадигм грамматических категорий. Получение таких аналогов способствует пониманию некоторых особенностей речи и помогает выработать единую логическую основу изучения знаковых систем.
Комбинаторная и квантитативная лингвистики. Выбор математического аппарата в лингвистических исследованиях – вопрос непростой. Его решение зависти в первую очередь от того, как определяется предмет и основные понятия языкознания и его теоретического ядра – структурно-математической лингвистики.
Некоторые математики и лингвисты считают, что предметом математической и структурной лингвистики должно быть изучение грамматики, порождающей текст. При этом грамматика понимается как конечное множество детерминированных правил, в том числе неграмматических, а язык рассматривается как бесконечное число регулярных цепочек слов, порождаемых этой грамматикой. При этом подходе экспликация лингвистических объектов должна опираться на такие разделы «неколичественной » математики как теория множеств, математическая логика (в особенности, теории рекурсивных функций и бинарных отношений), теория алгоритмов и т.д.
Что же касается «количественных» разделов математики (математическая статистика, теория вероятностей, теория информации, математический анализ), то они считаются либо неприменимыми для экспликации лингвистических явлений, либо играющими вспомогательную роль. На основе применения «неколичественного», или как его иногда называют, «качественного» математического аппарата в теоретическом языкознании сформировалось направление, условно называемое комбинаторной лингвистикой. Это направление противопоставляется квантитативной (количественной) лингвистике.
Методы детерминистского комбинаторного языкознания интенсивно разрабатываются в теории порождающих грамматик Хомского, в теоретико-множественных моделях Маркуса и в других лингвистических направлениях.
Однако математическое языкознание не может ограничиться детерминистской, неколичественной экспликацией лингвистических объектов.
Физик Н. Бор писал: «Мы не будем рассматривать чистую математику как отдельную область знания; мы будем считать ее скорее усовершенствованием общего языка…»
Усвоение науками отвлеченных понятий и методов математики расширяет их возможности, способствует открытию новых, более глубоких закономерностей. Первой среди гуманитарных наук на языке математики заговорила лингвистика. Системный характер языка, обобщенный характер его единиц - вот та благодатная почва, на которой стали плодотворно укореняться идеи и методы современной математики. Связь языкознания с математикой наметилась давно. Известный русский математик В.Я.Буняковский писал о необходимости применения математики в области грамматических и этимологических исследований. И.А. Бодуэн де Куртенэ, набрасывая контуры будущего языкознания, непременным условием его развития считал тесную и органическую связь с математикой. «Нужно чаще применять в языкознании количественное, математическое мышление и таким образом приблизить его все более к наукам точным». Перспективные мысли высказаны Бодуэном в статье «Количественность в языковом мышлении». Выдающийся лингвист практически использовал квантитативную методику в исследованиях по фонетике (исчисление альтернаций) и по грамматике (описание типов склонения). Крупнейший теоретик языка Е.Д. Поливанов также писал о точках соприкосновения между математикой и лингвистикой.
Связь языка с математикой не была односторонней. Используя методы математики, лингвистика в свою очередь питала математику плодотворными идеями. Наблюдения известного математика А.А. Маркова над текстом «Евгения Онегина» (распределение доли гласных и согласных среди первых 20 000 букв) привели к открытию знаменитых «марковских цепей», обогативших теорию вероятностей и математическую статистику. Примером использования лингвистических знаний в математике служит создание математической лингвистики.
Для описания и исследования лингвистических фактов привлекаются различные разделы математики: алгебра, теория множеств, математическая логика, теория информации, теория вероятностей и математическая статистика. В силу этого математическая лингвистика стала развиваться в нескольких направлениях - алгебраическая лингвистика, комбинаторная лингвистика, которая опирается на разделы «неколичественной» математики (теория множеств, математическая логика, теория алгоритмов), и квантитативная лингвистика, которая изучает лингвистические явления с помощью «количественной математики» (математическая статистика, теория вероятностей, теория информации и др.)
Квантитативная лингвистика отличается от математической лингвистики большим вниманием к языковой специфике, которая стоит за количественными отношениями. Главная ее задача - поиск связи между количественными и качественными сторонами языка: между употребительностью и возрастом слов, длиной слова и его употребительностью, полисемией и его употребительностью.
Пока наиболее перспективным представляется исследование сущностных характеристик языка при помощи аппарата теории вероятностей и математической статистики - квантитативная лингвистика. Собственно говоря, связь математики с языкознанием началась с попыток установить статистические свойства речи, поскольку языку присущи объективные количественные характеристики. Благодаря вероятностной природе языковой структуры, она легко поддается изучению математическим аппаратом теории вероятностей и математической статистики. Основа тому регулярность, упорядоченность языковых явлений.
Статистически исследуется фонетика, закладываются основы статистического изучения морфемного состава слова и морфологических категорий. В частности установлена связь между числом фонем и средней длиной морфемы, стало известно, что количество фонем отражается на качестве морфем и слов, а количество морфем на качестве слов.
С помощью формально-количественных методов изучается авторский идиостиль. Шире всего количественные методики используются при описании лексического уровня языковой системы. Практическим результатом статистического изучения лексики являются частотные словари, отличающиеся от обычных лингвистических (толковых, орфографических им других) тем, что словарные единицы располагаются в них не только в алфавитном порядке, но и в порядке убывающей частотности.
Характерно, что математические методы обладают следующими возможностями:
делают точными суждения, основанные на количественно-частотных соображениях
указывают на такие обстоятельства функционирования языка и диалекта, которые иными способами не обнаруживаются
позволяют глубже и всесторонне понять причины и результаты языковой эволюции, длительность эволюционных процессов и их хронологию, и даже прогнозировать будущее языковое развитие
расширяют сферу прикладного использования языкознания.
Количественная методика стала более эффективной с появлением вычислительной техники.
Точность в общественных науках определяется степенью адекватности отражения предмета и далеко не всегда выражается языком математики. Не количество математических формул на странице научного труда, а степень строгости определения элементарных структур и явлений, которые характеризуют данную область исследования, определяют точность научного поиска. «Точность достигается культурой специальных и точных исследований. Ни одна из точных наук не развивается путем создания общих курсов и монографий, а путем кропотливых, математически четких частных исследований». «Точность нужна в той мере, в какой она допускается природой материала. Излишняя точность может оказаться помехой для развития науки и понимания существа дела» (Лихачев Д.С. Литература-Реальность-Литература. - Л.,1981, с.196-197). Не голые цифры и не наукообразные формулы, а культура математического мышления нужна прежде всего гуманитарным наукам и языкознанию в частности. И вообще существо математики никоим образом не определяется числом (М.Хайдеггер).
Языкознание по существу занимает среди гуманитарных наук особое место, дав классические образцы научной точности. Так, по мнению ученых, сравнительно-историческое языкознание до сих пор остается примером точного лингвистического исследования. «Нет анализа более точного, чем языковой. В самые смутные вопросы лингвистика нередко вносит математическую прозрачность» (Осетров Е. Живая Древняя Русь. М.,1970, с.23).
Слова Гете «Я уважаю математику как самую возвышенную, полезную науку, поскольку ее применяют там, где она уместна, но не могу одобрить, чтобы ею злоупотребляли, применяя ее к вещам, которые не входят в ее область и которые превращают благородную науку в бессмыслицу», - чрезвычайно актуальны и в наше время – время взаимопроникновения наук.
3. Особенности естественного языка в сравнении с математическим Датский физик Нильс Бор говорил, что математика является значительно большим, чем наука, поскольку она является языком науки. И действительно, математика стала для многих отраслей знания не только орудием количественного расчета, но также методом точного исследования и средством предельно четкой формулировки понятий и проблем. С развитием науки возросло количество экспериментальных исследований. В связи с этим потребовалась разработка математической теории эксперимента, позволяющей так организовать наблюдения, чтобы при минимальном их числе получать максимальное количество информации об интересующем нас явлении или процессе. Роль математики в современном познании, современной практической деятельности так велика, что наше время называют эпохой математизации знаний.
Математика подобно любой науке многомерна. На когнитивном уровне она выступает как мышление, на перцептуальном – как чувствование, на лингвистическом – как язык. Лингвистическое измерение математики заслуживает особого рассмотрения. Дело в том, что лишь благодаря ему математике придается интерсубъективный, общезначимый для всех людей характер. Мышление и чувствование всегда индивидуально. Язык же является достоянием всех.
Как известно, язык – это система условных знаков, принятых в некотором сообществе и обеспечивающая коммуникацию его членов. Язык математики удовлетворяет этому определению. Подобно любому языку он состоит из совокупности высказываний (предложений). Особенность математического языка заключается в том, что в нем широко используются математические символы, объединяемые формулой. Учитывая это, часто говорят, что математика – это язык символов и формул. Впрочем, язык математики не сводится к символьным записям и утверждениям. В любом математическом труде используются такие слова и обороты , заимствованные из естественных языков: «предположим, что…», «и будем исходить из следующих аксиом» и т.п. Но в контексте математики этим словам и оборотам речи придается специфическое значение, которое сопрягается со смыслом формализованных утверждений.
Язык математики – это язык людей, имеющих дело с математическими структурами. В одних случаях речь идет непосредственно об этих структурах, в других на их основе разрешаются те или иные конкретные ситуации.
Язык математики часто сравнивают с естественным языком. При этом, как правило, дается восторженная характеристика одного из них. Следует учитывать, что речь идет о различных языках. В случае математических структур для их описания необходим язык математики; на его фоне естественный язык громоздок и двусмыслен. В житейских ситуациях естественный язык имеет преимущества перед математическим языком и ясно, почему: здесь можно обойтись без детальных знаний о математических структурах. Естественный язык не нуждается в замене математическим языком. Существует другое – не усвоивший язык математики не воспользовался благоприятнейшими возможностями своего личного развития. Самое интересное состоит в том, что в общении друг с другом людям то и дело приходится переходить с естественного языка на язык математики и обратно. С различными переходами связаны также междисциплинарные функции математики.
До тех пор пока исследователь находится в пределах чистой математики, он обходится математическим языком. При этом ему нет нужды обращаться к каким – либо другим языкам. Ситуация редко изменяется, когда строятся так называемые математические модели тех или иных (физических, биологических, социальных и т.п.) явлений. Математические модели строятся из терминов, интерпретированных в конкретную объектную область, являющуюся предметом той или иной конкретной науки. Использование математических моделей переводит чистую математику в прикладную.
Итак, в математике как таковой используется математический язык. В конкретной науке используется язык данной науки (в лингвистике – язык лингвистики, в экономике – язык экономики). В прикладной математике, т.е. в случае математических моделей, используются два языка: математический язык плюс язык конкретной науки.
Как же устроен математический язык? Прежде всего это язык абстрактный, в противоположность нашим конкретным языкам, где каждое слово имеет конкретное значение. Язык математических формул и знаков обладает большей универсальностью и используется во всех сферах человеческой деятельности. Система математических знаков является достоянием всего человечества, она вырабатывалась на протяжении тысячелетий. Математический язык – это результат совершенствования естественного языка по различным направлениям: устранение громоздкости и двусмысленности естественного языка, расширение его выразительных возможностей. Он употребляется как средство выражения математической мысли. Язык в широком смысле – это словарь, грамматика, рассказы, повести, пьесы и романы, написанные на этом языке. Что же в математическом языке является аналогом слов и грамматики, а что – рассказов и повестей? Аналог слов и грамматики – математическая операционная система, а рассказов и прочего – математические модели.
Овладение математическим языком предполагает сознательное усвоение содержания математических понятий, отношений между ними (аксиом, теорем) и умение рационально и грамотно выразить математическую мысль в устной и письменной форме с помощью средств математического языка, а также свободное оперирование математическими знаниями, умениями, навыками на практике.
Овладение математическим языком формирует навыки рационального выражения мысли: последовательность, точность, ясность, лаконичность, выразительность, экономность, информированность. Сознательное и свободное владение математическим языком является условием и средством овладения математической культурой. Преимущества математического языка заключаются в следующем: во-первых, по сравнению с естественным языком он обладает большей точностью, во-вторых, благодаря использованию специальных терминов и формул его способ выражения более краток и более нагляден, чем способ выражения естественного языка.
Из названных выше преимуществ вытекает самое важное: без помощи математического языка такие науки как физика и лингвистика не смогли бы достичь сегодняшнего уровня, потому что человек не в состоянии понять сложные связи этих наук на естественном или специально-научном не символическом языке. Уже перевод относительно простых формул на естественный язык создает иногда такие сложные образования, что они почти непонятны. Поясним это на примере из математики. Для области рациональных чисел действителен так называемых закон коммутативности сложения, выраженный в формуле а+ b=b+a. Словами это было бы выражено так: «Если любое число прибавить ко второму, то сумма будет равна сумме этих же чисел, если бы второе число прибавили к первому». Хотя речь идет об очень простом законе, становится ясно, что с помощью формулы его можно выразить короче, яснее и точнее.
Недостатками математического языка являются его специфичность и ограниченная возможность отображения.
Основные расхождения между естественными и математическим языками связаны с различным построением языкового знака и знака математического.
Во-первых, лингвистический знак (слово, словосочетание, предложение) обычно включает в себя четыре компонента – имя (материальный носитель информации), денотат (отражение предмета из внешнего мира), десигнат (понятие о предмете) и коннотат (комплекс чувственно-оценочных оттенков, связанных с предметом и понятием о нем); знак математического языка включает только имя и десигнат (математическое понятие); сказанное иллюстрирует рис.1
Рис.1
Во-вторых, лингвистический знак многозначен, математический знак имеет, как правило, одно концептуальное значение.
В-третьих, лингвистический знак потенциально метафоричен, у знака математического метафоричность полностью отсутствует.
Все эти свойства лингвистического и математического знаков можно проследить. Сравните значение математического знака 3 и слова тройка. Если 3 имеет единственное десигнативное математическое значение – «3 любых объекта», то слово тройка имеет несколько значений: «цифра три», «оценка в три балла», «упряжка из трех лошадей», «группа из трех человек», «разновидность мужского костюма» ит.п. При этом в значении слова тройка содержатся не только указанные десигнативные понятия, оно может указывать на конкретный предмет, например, на вполне определенный костюм. Одновременно это слово несет дополнительные коннотативные метафорические оттенки, связанные с такими словосочетаниями как «Бог троицу любит», «дохлая тройка», «с третьей попытки» и др.
Из всего сказанного вытекает еще одно важное различие между десигнативными значениями математического и лингвистического знаков.
Значение каждого математического знака можно легко представить в виде множества элементов, причем такое множество имеет вполне четкие границы: значение знака 3 является множеством, охватывающим такие конкретные совокупности, которые включают только три (не пять, не восемь) предметов.
Иначе организовано десигнативное значение лингвистического знака – и оно также может рассматриваться как множество денотатов, однако это множество не всегда имеет четкие границы. Так, например. Не удается определить смысловые границы слов синий и зеленый. Разные люди в зависимости от особенностей своего хроматического зрения будут называть показываемые им конкретные синие оттенки то синим, то зеленым цветом. Также нельзя указать точную временную границу, разделяющую значения слов ночь и утро. Иными словами, значения лингвистических знаков представляют собой нечеткие множества с размытыми границами. Особенности построения лингвистического знака приводят к тому, что естественный язык представляет собой нежестко организованную диффузную систему, которая воспринимается и используется человеком в значительной мере интуитивно.
Основными недостатками естественного языка являются следующие:
1.Слова естественного языка со временем постепенно и почти незаметно меняют свое значение.
2.В естественном языке часто бывает, что одно слово одновременно имеет два или более различных значений и одновременно обозначает различные предметы, но бывает также, что различные слова имеют одно и то же значение, обозначают один и тот же предмет. Слово «церковь» обозначает, например, и здание церкви, и вид религии. Различные слова, например, «превосходство» и «перевес» или «катастрофа» и «катаклизм» имеют одно и то же значение.
3.Значение слов естественного языка часто бывает расплывчатым, неопределенным, т.е. не всегда можно сказать об определенном предмете, что слово обозначает именно его. Часто, например, нельзя сказать о человеке, здоров он или нет. В таком случае помогают себе неопределенной формулировкой: он не совсем здоров.
4. Наконец, употребляемые грамматические правила построения выражений естественного языка в логическом смысле также несовершенны, не в любом случае можно определить, имеет данное предложение смысл или нет.
Напротив, язык математики является хорошо организованной системой, существующей и функционирующей в виде логического построения, каждый элемент которого имеет осознанную значимость.
Конфронтация естественного языка и языка математики требует, чтобы каждому лингвистическому объекту был поставлен в соответствие некоторый математический объект. Лингвистический знак, например, словосочетание или слово и составляющие этот знак фигуры – фонемы, буквы, слоги - должны интерпретироваться с помощью знаков математических. Эта математическая интерпретация связана с расчленением лингвистического объекта и выделением в нем одного смыслового или сигнального компонента, который становится предметом дальнейшего исследования. Остальные сигнальные и смысловые элементы лингвистического объекта исключаются.
4.Формирование математической компетенции лингвистов
В ХХ веке ранее неустойчивый союз математики и гуманитарных наук укрепился настолько, что появилась насущная потребность учитывать его наличие в вузовском образовании.
Первой на языке математики заговорила лингвистика. Пример великих языковедов Ф. де Соссюра, Ф.Ф.Фортунатова, И.А. Бодуэна де Куртенэ, Е.Д.Поливанова, Н.С.Трубецкого, Т.П.Ломтева убеждает в том, что лингвисту необходима не просто математика, а именно математика высшая.
На филологических отделениях в течение первого семестра читается предмет «Основы высшей математики». В учебные планы вузов введены такие курсы, как математическая лингвистика, функциональная грамматика, методы математического анализа в лингвистике.
Так в чем же проблема? Их несколько. Сначала остановимся на той, которую определяет парадоксальная ситуация: с одной стороны, скептицизм самих математиков, считающих невозможным корректное использование математических методов в лингвистике, с другой – предубеждение самих филологов против математики,
Действительно, студенты филологических отделений отрицательно относятся к изучению математики в качестве компонента своей профессиональной подготовки. Так, например, результаты опроса, проведенного нами среди студентов-русистов и корееведов первого и второго курсов об их отношении к дисциплине «Основы высшей математики», показывают следующее: 64% (первый курс) и 61 % (второй курс) - отрицательно относятся к данному предмету. Если в вопросе спрашивалось отношение только к математике, то отрицательное мнение выразили около 100% опрашиваемых. Следует также отметить, что соответственно 58% и 61% из них не понимают целей изучения высшей математики применительно к филологическим специальностям. Причины при этом называются совершенно разные. Мы позволим себе перечислить здесь лишь некоторые из них.
1.Дидактические причины. Математические дисциплины преподносятся студентам-филологам в дидактически неудачной форме, в слишком формализованном, абстрактном виде. Студенты не улавливают связи между математическими знаниями и практическими задачами в своей будущей профессиональной работе. Напрашиваются следующие выводы и предложения: надо насытить курсы яркими примерами задач из реальной практики учителей словесности, не стесняясь при этом заимствований из лучших западных учебников, написанных под заголовками «Математическая статистика для педагогов», «Математика без формул для лингвистов».
2.Невостребованность математики преподавателями других лингвистических курсов и научными руководителями курсовых и выпускных квалификационных работ. Многие курсовые и выпускные квалификационные работы получают отличные оценки либо при полном отсутствии математического аппарата, либо при наличии грубейших ошибок, допущенных при попытках его использования. Некоторые преподаватели открыто выражают на лекциях и семинарах свое скептическое, негативное отношение к математическим методам и подходам в той области общей и прикладной лингвистики, которую преподают студентам. Данная установка подкрепляет то негативное отношение к математике, которое имеется у значительной части студентов. Выводы и предложения: необходимо изменять отношение к математическим методам, прежде всего у самих преподавателей, включая не только методические дискуссии, но и курсы повышения квалификации. Целый спектр предложений по данной линии связывается с внедрением в курсовые и выпускные квалификационные работы обязательных требований к использованию математического аппарата: от более сильного предложения – сделать «математическую культуру» компонентом оценки всякой работы, без которого нельзя поставить высший балл, до умеренного — обязать каждого студента факультета выполнить хотя бы одну из курсовых работ с использованием статистической обработки данных.
3. Доминирование нематематизированных методов в современной отечественной лингвистике и дидактике. В эпоху, когда существовала развитая система научных учреждений и относительно более высокое финансирование науки, будущая карьера выпускников филологических факультетов во многом связывалась с научной стезей – с защитой диссертаций, выполнением научных исследований. Сейчас приоритеты существенно изменились. Хотя по-прежнему считается, что математика – атрибут научной работы, без которого трудно защитить диссертацию, но на практике – в процессе защите магистерских диссертаций, прохождения различного рода аттестаций, математика как будто и не требуется. Авторы учебных программ и пособий также пока недостаточно широко используют математические методы. Не реализуются межпредметные связи с математикой в практике преподавания родного и иностранного языков, так как отсутствует разработанная методика проведения подобного рода интегрированных уроков. Внедрение элементов математического аппарата могло бы упростить систему контроля знаний, умений и навыков учащихся, освободить преподавателей от перегрузок, связанных с проверкой студенческих работ. Введение рейтинговой системы также требует от современного преподавателя математической точности при оценке результатов деятельности учащихся. Представляется целесообразным сформулировать основные методические рекомендации, обеспечивающие эффективную математическую подготовку будущих лингвистов:
Для понимания материала студентам филологических специальностей не нужно никаких предварительных знаний, может быть, кроме некоторых основ школьной программы. Материал должен быть максимально замкнутым в себе, чтобы для его понимания не нужно было обращаться к другим учебникам в поисках неразъясненных понятий.
Изложение должно быть строго последовательным и достаточно строгим, чтобы можно было делать однозначные выводы; вестись с использованием точного формализованного языка, что в значительной степени экономит мыслительный процесс.
Студент должен научиться понимать и применять математические понятия, подходы, методы и сам математический формализм не только для построения математических, но и более строгих вербальных (словесных) моделей в различных областях лингвистических исследований.
Таким образом, математизация филологического знания является оборотной стороной гуманитаризации естественных наук. Данный процесс ориентирован не только на обучение математическому мышлению, но и на развитие с помощью математики самого профессионального мышления лингвистов.
Литература
1.Розов Н.Х. Гуманитарная математика // Вестник Московского университета. Серия 20. Педагогическое образование.-2004, № 2. С.37-52.
2. Хант Дж. Вычислительная лингвистика в Летнем Институте лингвистики // Вопросы языкознания.-1993, №6. С.114-125.
5. Множество лингвистических объектов.
Одно из основных понятий современной математики – понятие множества. Данное понятие является первичным, т.е. не поддается определение через другие, более простые понятия.
Множество – это набор, совокупность каких-либо объектов, обладающих общим для всех их характеристическим свойством.(Например, множество зданий города Ташкента, множество планет Солнечной системы, множество букв русского или узбекского алфавита ит.д.).
Это определение понятия множества не являются в полном смысле слова логическим определение, а всего лишь пояснением. «Множество» - это самое широкое по объему понятие математики и математической логики.
Само понятие множества и понятие «элемент» (член множества) введены в научный обиход немецким математиком Георгом Кантором (1845-1918).По его словам «множество есть многое, мыслимое нами как единое». Данное определение множества носит интуитивный характер.
Естественно, что понимание множества за минувшие десятилетия претерпело изменения. К примеру, известный английский математик П.Кон множеством называл те классы, которые являются членами других классов.
Какова же структура множества, чем одно множество отличается от других, какие математические и логические операции совершаются ч множествами?
Прежде всего, множества состоят из определенного набора объектов, которые называются элементами множества. При этом каждый из объектов данного вида либо принадлежит, либо не принадлежит данному множеству. Так, например буква A принадлежит множеству букв, образующих русский алфавит. В то же время буква А этому множеству не принадлежит.
Множества, включающие только такие объекты, принадлежность или непринадлежность которых к тому или иному множеству не вызывает сомнений, называются четкими множествами. Подобные множества всегда имеют ясно очерченные границы.
Четким множествам противопоставлены нечеткие или «лингвистические множества». Нечеткие множества включают в себя такие объекты, которые могут быть отнесены к тому или иному множеству лишь с определенной степенью достоверности. Так, например, ряд исследователей произведение Пушкина относя к множеству «повести», а другие – к множеству «романы».
Множества, которые состоят из конечного числа элементов, называются конечными множествами. К числу конечных относятся также и пустые множества, которые не содержат ни одного элемента. Например, множество двухбуквенных сочетаний бй, чы, ой можно считать пустым, если иметь в виду только русские тексты.
Лингвистика чаще всего имеет дело с конечными множествами объектов. Однако приходится рассматривать и бесконечные множества. Например, бесконечным является множество всех словоупотреблений в текстах данного языка при условии, что этот язык беспрерывно порождает и будет порождать новые тексты без какого-либо ограничения во времени.
То, что мы называем значением слова (а их обычно у слова бывает несколько), можно представить в виде множества семантических элементов. Языковеды называют их семами. Сема – простейшая единица значения, которая выделяется в результате лингвистического анализа. Первым представил значение слова в виде множества датский глоссематик Хьюго Ульдалль. Для этого он использовал нехитрую математическую символику. Например: Мальчик = {человек + мужского пола + несовершеннолетний}.
Для обнаружения семантических элементов в значении слова необходим специальный анализ. Чтобы получить представление о структуре значения какой-нибудь единицы, нужно ее сравнить с другими сходными единицами, взять соответствующий класс (множество М) обозначаемых предметов. Пусть нам предстоит определить, из каких смысловых частиц складывается значение слова отец как термина родства (другие значения слова в расчет не принимаются).Этому слову, как и другим, образующим множество обозначений родства, свойственна общая семантическая доминанта «родственник/родственница» (общая сема - С): отец, мать, сын, дочь, дедушка, бабушка, дядя, тетя, племянник, племянница, двоюродный дедушка, двоюродная бабушка, внучатый племенник, внучатая племянница. Для простоты анализа ограничимся этими словами, всего же в русском языке, по данным Л.А.Новикова, насчитывается более ста наименований лиц, находящихся в различных родственных отношениях. Сопоставляя друг с другом указанные слова, мы находим, что все множество таких имен может быть разбито на непересекающиеся подмножества по четырем основаниям.Эти основания разбиения множества и соответствуют семам. Вот они:
| Разбиения множества | Семантические элементы |
| 1 разбиение | 1 – мужской пол 2 – женский пол |
| 11 разбиение | 1 – родитель 2 – рожденный |
| 111 разбиение | 1 – прямое родство 2 – косвенное родство |
| 1У разбиение | 1 – первое поколение 2 – второе поколение |
Пользуясь данной таблицей, мы можем определить значение каждого из представленных выше терминов родства:
| 1 | 1 | 2 | 1 | 2 |
| 11 | 1 | 1 | 2 | 2 |
| 111 | 1 | 1 | 1 | 1 |
| 1У | 1 | 1 | 1 | 1 |
| М | отец | мать | сын | дочь |
6. Основные операции над лингвистическими множествами.
Основными операциями, осуществляемыми над множествами, являются сложение, умножение и вычитание. Эти операции не являются тождественными одноименным арифметическим, производимым над числами.
Объединением или суммой двух множеств называется множество, содержащее все такие и только такие элементы, которые являются элементами хотя бы одного из этих множеств. Объединение множеств в математике записывается так: А + В.Если одни и те же элементы содержатся в обоих множествах, то в сумму А+В эти элементы входят только по одному разу. Например, рассмотрим слова женщина и врач как лингвистические множества, состоящие из семантических элементов. Женщина = {человек + женского пола}. Врач = {человек + имеет медицинское образование + лечит больных}. Сумма данных множеств дает новое понятие «женщина-врач» и состоит из 4 элементов , а не из пяти, как это имело бы место при сложении чисел. Графически данная операция может быть представлена следующим образом:
2 3 2 3
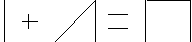
1 1 4 1 4
Пересечением (или умножением) двух множеств А и В (обозначается АВ) называется множество тех элементов, которые принадлежат и к А , и к В. Обозначим множества семантических элементов, входящих в семантическую группу «Возраст» в1 – несовершеннолетний в2 – молодой в3 – старый. Результат пересечения данного множества со словом мужчина {человек, мужской пол} представим графически:
1 в1 в2 в3 1в1 1в2 1в3
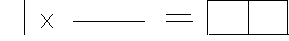
2 2в1 2в2 2в3
Новое множество АВ, полученное в результате умножения, называется произведение.
Разностью двух множеств А и В называется множество всех таких элементов множества А, которые не содержатся во множестве В .Разность множеств обозначается А – В. Так, если мы обозначим множество русских гласных {а,о,у,э,и,ы} через В, а множество огубленных гласных {о, у} через А, то В – А = {а,э,и,ы}.
Основные операции над лингвистическими множествами
Основными операциями, осуществляемыми над множествами, являются сложение, умножение и вычитание. Эти операции не являются тождественными одноименным арифметическим, производимым над числами.
Объединением или суммой двух множеств называется множество, содержащее все такие и только такие элементы, которые являются элементами хотя бы одного из этих множеств. Объединение множеств в математике записывается так: А + В.Если одни и те же элементы содержатся в обоих множествах, то в сумму А+В эти элементы входят только по одному разу. Например, рассмотрим слова женщина и врач как лингвистические множества, состоящие из семантических элементов.
Женщина = {человек + женского пола}.
Врач = {человек + имеет медицинское образование + лечит больных}. Сумма данных множеств дает новое понятие «женщина-врач» и состоит из четырех элементов, а не из пяти, как это имело бы место при сложении чисел. Графически данная операция может быть представлена следующим образом:
2 3 2 3
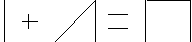
1 1 4 1 4
Пересечением (или умножением) двух множеств А и В (обозначается АВ) называется множество тех элементов, которые принадлежат и к А, и к В. Обозначим множества семантических элементов, входящих в семантическую группу «Возраст» в1 – несовершеннолетний; в2 – молодой; в3 – старый. Результат пересечения данного множества со словом мужчина {человек, мужской пол} представим графически:
1 в1 в2 в3 1в1 1в2 1в3
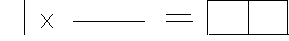
2 2в1 2в2 2в3
Новое множество АВ, полученное в результате умножения, называется произведением.
Разностью двух множеств А и В называется множество всех таких элементов множества А, которые не содержатся во множестве В. Разность множеств обозначается А – В. Так, если мы обозначим множество русских гласных {а, о, у, э, и, ы} через В, а множество огубленных гласных {о, у} через А, то В – А = {а, э, и, ы}.
Использованная литература
1.Арапов М.В.Квантитативная лингвистика.-М.,1988.
2.Арапов М.В., Херц М.М. Математические методы в исторической лингвистике.-М., 1974.
Головин Б.Н.Язык и статистика.М., Просвещение,1971.
Журавлев А.Ф. Лексикостатистическое моделирование системы славянского языкового родства.-М., 1994.
Крейдлин Г.Е., Шмелев А.Д. Математика помогает лингвистике: Кн. Для учащихся.- М., 1994.
Носенко И.А. Начала статистики для лингвистов.М.,Высшая школа, 1981.
Пиотровский Р.Г.,Бектаев К.Б.,Пиотровская А.А. Математическая лингвистика.-М., Высшая школа, 1977.
Сухотин Б.В. Исследование грамматики числовыми методами.-М., 1990.
Хант ДЖ. Вычислительная лингвистика в Летнем Институте лингвистики//Вопросы языкознания.1993.№6.С.114-125.
Фрумкина Р.М. Сатистические методы изучения лексики.М., Наука, 1964
7.Понятие функции в лингвистике.
Нам уже не раз приходилось сравнивать различные лингвистические и нелингвистические множества. Сопоставление множеств приводит к понятию соответствия, которое подобно понятию множества является одним из основных понятий математической лингвистики.
Рассмотрим вопрос о соответствии множеств на примере одного из звуковых законов в истории русского языка.
В древнейшую эпоху действовал закон, по которому согласные Г, К, Х перед гласными переднего образования изменялись в мягкие шипящие Ч, Ж, Ш (явление палатализации): рука – поручити, друг – дружити, сух – сушити. В более поздний период этот закон перестал действовать. Представим согласные Г, К, Х как множество А, а соответствующие им мягкие шипящие Ч, Ж, Ш в виде множества В. Между множествами А и В имеется соответствие, которое описано в истории русского языка как смягчение согласных, или палатализация. Каждому звуку в множестве А соответствует определенный звук в множестве В. При этом переход от звуков множества А к звукам множества В совершается по четко определенному правилу: согласные звуки смягчаются.
Если два множества находятся в таком соответствии, что каждому объекту х из множества А ставится в соответствие некоторый определенный объект у из множества В, то говорят, что между А и В существует функциональная зависимость.
Правило f , пор которому можно перейти от объекта х Є А к соответствующему ему объекту у Є В, называется функцией. Наш пример со смягчением согласных можно рассматривать как пример лингвистической функции.Для обозначения функции используется запись у = f (х).
Если соответствие между двумя множествами установлено, то принято говорить, что на множестве А задана функция со значениями, при -надлежащими множеству В. Объекты х множества А, которым поставлены в соответствие элементы множества В, называются значениями аргумента (или значениями независимой переменной).В нашем случае это согласные Г, К, Х, Все множество А называется множеством значений аргумента, или областью определения (существования) функции f(х).
Рассмотрим природу функциональной зависимости в языке на примере типологии предложений по цели высказывания с помощью аппарата математического анализа.
По функции заключенного в них высказывания предложения делятся на повествовательные, вопросительные и побудительные. Они служат соответственно для передачи трех основных форм мысли – суждения, вопроса, побуждения. Суждения, требования и вопросы являются отражением объективных связей вещей или явлений.
| Повествовательное предложение | Побудительное предложение | Вопросительное Предложение |
| Суждение | Требование | Вопрос |
| Объективные связи между предметами | Объективные связи между предметами | Объективные связи между предметами |
Как видно из таблицы, повествовательное, побудительное и вопросительное предложения отличаются друг от друга прежде всего по своей функции. Повествовательные предложения носят информативный, описательный, десигнативный характер. Они дают сведения о прошлом (например, свидетельские показания в суде), о настоящем (например, сведения о магнитном поле Земли) или о будущем (например, в прогнозе погоды).
Побудительные предложения носят направляющий, указывающий, предписывающий, определяющий характер, Они побуждают кого-либо к действию или к его прекращению.В форме данных предложений можно сформулировать планы, юридичесие законы и нравственные нормы.
Вопросительные предложения выражают желание что-либо узнать. В зависимости от того, хотят ли узнать о том, что есть или было или что надо делать, ответ следует в виде повествовательного или побудительного предложения.
Предложения всех трех функциональных типов могут быть эмоционально окрашенными. Повествовательные предложения, в отличие от других типов, не требует ответной реакции адресата:
1.Повествовательное предложение не требует ответной реакции адресата(V1).
2.Побудительное предложение побуждает к действию(V2).
3.Вопросительное предложение требует ответа(V3).
Соответственно функциональное содержание системы предложений по цели высказывания может быть представлено в виде следующей таблицы:
| F | V1 | V2 | V3 |
| 1 | 1.V1 | 1.V2 | 1.V3 |
| 2 | 2.V1 | 2.V2 | 2.V3 |
| 3 | 3.V1 | 3.V2 | 3.V3 |
Теперь охарактеризуем каждую из функциональных разновидностей предложений, взятую в отдельности.
1.V1 – собственно повествовательное предложение. Например, Пришла весна.
1.V2 – повествовательно – побудительные предложения (в ситуации «начальник-подчиненный», «учитель - ученики» и т.п.). Например, Петров идет к доске, Сидоров готовится к ответу.
1.V3 – повествовательно-вопросительные предложения (обычно названия произведений, заголовки статей и т.п.). Например , «Что я видел во сне…»
(рассказ Л.Н.Толстого) «Кому на Руси жить хорошо» (поэма Н.А.Некрасова).
2.V1 – побудительно-повествовательное предложение. Например, Приходи скорей, весна! (Ср.: Хочу, чтобы скорей пришла весна.)
2.V2 – собственно побудительное предложение. Например, Давайте готовиться к приходу весны!
2.V3 - побудительно-вопросительное предложение. Например, Перестанешь ты смеяться, наконец!
3.V1 - вопросительно-повествовательное предложение. Например, Кто из нас заранее не радовался приходу весны? (Ср.: Все мы заранее радуемся приходу весны.)
3.V2 – вопросительно-побудительное предложение. Например, Не подскажете, который час? (Ср.: Подскажите, который час.)
3.V3 – собственно вопросительное предложение. Например, Готовитесь ли вы к приходу весны?
Таким образом, функциональную характеристику системы предложений по цели высказывания можно представить в виде следующей таблицы, где А –повествовательное предложение, В – побудительное, С – вопросительное:
| Х | А | В | С |
| А | А | АВ | АС |
| В | ВА | В | ВС |
| С | СА | СВ | С |
При взгляде на данную таблицу обращает на себя внимание наличие в системе обратных функций ВА = 2.V1, СА = 3.V1, СВ= 3.V2. Явление обратных функций в грамматике будет рассмотрено в следующем параграфе.
8.Учет обратных функций при обучении языку и переводу.
В речевой деятельности нам приходится постоянно сталкиваться с антиномичностью грамматических категорий, обусловленной их диалектической природой. При изучении языковой системы акцент традиционно делается на языковой норме и не всегда на контекстном употреблении языковых единиц. Между тем наличие в естественном языке определенной стабильности словоупотребления, само существование языковой нормы объясняется естественным отбором, закрепляющим наиболее частые ситуации наименования как языковые штампы. На глубинном уровне языковой системы обнаруживаются отчетливые механизмы, лежащие в основе выбора контекстных значений. Эти механизмы выглядят более системно, если рассматривать их как имеющие математическую природу и функциональный характер. Существование функций в грамматике связано с противоречивостью, двойственностью языка и речи. В лингвистике общеизвестно положение Ф. де Соссюра о двойственности языка и речи, из которого вытекает недостаточность любого одностороннего подхода к изучению языка. Соссюр даже настаивал на необходимости разработки двух лингвистик – лингвистики языка и лингвистики речи. Однако в традиционной лингводидактике по-прежнему акцентируется лишь один из аспектов системы изучаемого языка. Более того, положение Соссюра часто трактуется как необходимость отдельно изучать явления речи и явления языка. Хотя такая трактовка в ряде случаев практически уместна, все же смысл двойственности языка и речи не в их отдельном разграниченном существовании как явлений, но скорее в дополнительности этих аспектов языка в целом.
В некоторой степени преодолеть этот разрыв может функциональное описание грамматики. Существование обратных функций в грамматике рассматривается нами как одно из закономерных проявлений противоречивой природы языка, подчиненной основному тезису диалектики: если есть что-нибудь одно, то должно быть нечто иное, противоположное ему. В грамматике любого действующего языка существует ряд явлений, подчиняющихся данной закономерности. Так, например, в морфологии известны случаи контекстного употребления формы изъявительного наклонения глаголов в функции повелительного, например: «Дежурный заболел, а ты его заменишь» (= ты его замени). Здесь налицо функциональная зависимость А → В, где А – изъявительное наклонение , а В – повелительное. Теперь рассмотрим обратную функцию В → А, т.е. употребление формы повелительного наклонения в значении изъявительного, например: «Вот в эту-то Дуняшу и влюбись (влюбился) Аким!» (Тургенев). Для сравнения также приведем пример контекстного употребления формы повелительного наклонения в значении сослагательного (С) – В → С: «Приди ты на час раньше, ничего этого не случилось бы» (= пришел бы ты на час раньше). Обратная функция для данного случая С → В : «Вы бы, доктор, шли спать!» (Чехов). Функция А → С (транспозиция словоформы изъявительного наклонения в семантическую сферу сослагательного): «Ах, какой ты, Федя, ну, послал кого за водкой – и все тут!» (Мамин-Сибиряк) (= ну, послал бы). Обратная функция С → А для данного случая (транспозиция словоформы сослагательного наклонения в семантическую сферу изъявительного) : «Мне хотелось бы поехать» (= я хочу поехать).
При изучении категории времени глагола обратные функции могут быть также рассмотрены аналогичным образом. Обозначим настоящее время глагола как А, прошедшее как В, будущее – С. Задаем функцию
А → В (настоящее – прошедшее): В 1884 г. П.И. Чайковский пишет оперу «Евгений Онегин». Обратная функция (прошедшее – настоящее): Талант и бездарность не уживаются. Там, где восторжествовал талант, бездарности делать нечего (Тендряков). Функция В → С (транспозиция словоформы прошедшего в сферу будущего): Если он не вернется, мы пропали (= мы пропадем). Обратный случай (будущее – прошедшее): Кругом не слышалось почти никакого шума… Лишь изредка в близкой реке с внезапной звучностью плеснет большая рыба, и прибрежный тростник слабо зашумит, едва поколебленный набежавшей волной (Гоголь).
Рассмотрим транспозицию словоформы настоящего времени в сферу будущего (А → С) и обратную ей функцию С → А (будущее → настоящее). Например: Завтра магазин не работает. − Хорошо сидеть и прислушиваться к тишине: то ветер подует и тронет верхушки берез, то лягушка зашелестит в прошлогодней листве, то за стеной колокольни часы пробьют четверть…(Чехов) (= то дует, то трогает, то шелестит, то бьют…). Общая картина функциональной характеристики системы временных форм глагола, описанная выше, может быть представлена в виде математического графа.
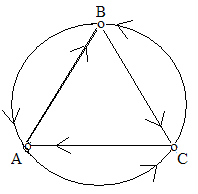
Явление обратных функций на уровне морфологических категорий требует глубокого и всестороннего изучения на широком и разнообразном языковом материале и должна обязательно учитываться при изучении морфологии по принципу «от средств к функциям». Демонстрация перехода формы от одной функции к другой раскрывает взаимосвязь лексики и грамматики, а также семантические особенности словоформ в контексте. Подобного рода функциональный подход может быть успешно использован в изложении курса грамматики и лексикологии, при обучении языку и переводу. Если первичные функции сопоставляемых языковых единиц двух языков совпадают в объеме, то факты усваиваются легко и ошибки не имеют места. Они возникают преимущественно в том случае, когда в изучаемом или родном языке языковые единицы используются во вторичных и обратных функциях, ибо здесь язык проявляет свою специфику. Например, артикли во
французском и английском языках используются одинаково в их первичной функции, тогда как во вторичных могут быть существенные расхождения. Аналогичная ситуация и в области перевода. При использовании в двух вариантах слов или форм в первичных функциях (с одинаковым объемом значений) можно переводить дословно, если же языковые единицы использованы во вторичных функциях, то могут возникнуть трудности в переводе. Например: Три и пять будет восемь нельзя перевести на французский *Trois et cinq f e r o n t huit (в отличие от русского языка, будущее время не может быть здесь использовано для передачи вневременного значения). Таким образом, функциональный подход может быть надежной основой для теории и практики перевода.
9.Применение математических графов в лингвистике.
С середины прошлого века началось интенсивное внедрение математических методов в лингвистику. Наиболее простым и мощным средством математизации лингвистических дисциплин стала теория графов.
Графом в математике считается конечная совокупность точек, именуемых вершинами; некоторые из которых соединены друг с другом линиями, называемыми ребрами графа.
Графы часто используются при решении логических проблем, связанных с перебором вариантов, а также для описания связей между структурными элементами различных по своей природе объектов.
В языкознании математические графы особенно успешно применяются в исследованиях по семантике и синтаксису.
Так, например, семантические единицы (семы) легко могут быть представлены в виде вершин графа, а связи между ними – с помощью
линий.
Например: мальчик ={человек +мужского пола + несовершеннолетний}.
Или: сверкать = {излучать + свет + яркий} (см. рис. 1).
Рис. 1
2
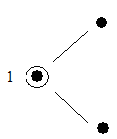
3
С графами, подобными приведенным выше, могут производиться операции сложения, вычитания, умножения и деления. К примеру, операция умножения семантических единиц может быть представлена следующим образом, при условии, что 1 = человек; 2 = мужской пол; V1 = несовершеннолетний; V2 = совершеннолетний; V3 = старый (см. рис. 2).
Рис.2
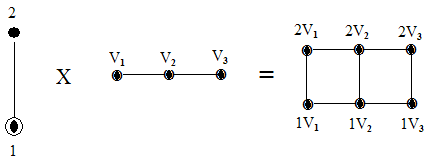
Получаем: 2V1 = мальчик; 2V2 =юноша; 2V3 = старик.
В морфологических исследованиях графы могут быть использованы для функциональной характеристики грамматических категорий. В данном случае вершинам графа присваиваются различные значения: наклонение, время глагола, формы грамматического рода и др.. Так, например, присвоив вершинам графа значения форм наклонения глагола, где А = изъявительное наклонение; В = повелительное наклонение; C = сослагательное наклонение, (см. рис. 3), имеем маршруты графа АВ ( изъявительное наклонение в функции повелительного), например: «Давайте откроем учебники и найдем с вами упражнение № 8!»; ВА (повелительное наклонение в функции изъявительного), например: «Иванов напроказил, а Петров за него отвечай», «Вот в эту-то Дуняшу и влюбись Аким!» (Тургенев); АС (изъявительное наклонение в функции сослагательного), например: «Вода закипает при температуре 100 градусов по Цельсию». Повелительное наклонение в функции условного (ВС): «Да будь и я негром преклонных годов, и то без унынья и лени я русский бы выучил…» (Маяковский); сослагательное наклонение в функции повелительного (СВ) : «Вы бы, доктор, шли спать!» (Чехов) (см. рис. 3).
Рис.3
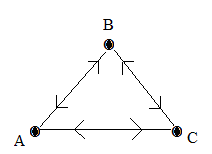
Присвоив вершинам графа-треугольника значения предложений по цели высказывания, получаем функциональную характеристику типологии предложений, при условии, что А - повествовательное предложение, В – вопросительное, С – побудительное. Итак, маршрут графа АВ (повествовательное предложение в функции вопросительного) : «Лекция на тему «Есть ли жизнь на Марсе» состоится завтра»; маршрут ВА (вопросительное предложение в функции повествовательного): «Кто из нас не знает Пушкина?» в смысле «Все мы знаем Пушкина». ВС – «Не передадите ли мне солонку?»; АС – «Петров поедет завтра в Москву» (в ситуации «начальник - подчиненному»); СА – «А он возьми и упади на ровном месте».
Существуют также способы представления синтаксического строения предложений с помощью графов с целью изучения функциональных стилей языка, индивидуального стиля писателя, синтаксической омонимии. Графы могут быть использованы и в методическом аспекте на этапе презентации грамматического материала в соответствии с основными дидактическими принципами доступности, наглядности, интегрированности обучения.
Библиография
1.Арапов М.В.Квантитативная лингвистика.-М.,1988.
2.Арапов М.В., Херц М.М. Математические методы в исторической лингвистике.-М., 1974.
Головин Б.Н.Язык и статистика.М., Просвещение,1971.
Журавлев А.Ф. Лексикостатистическое моделирование системы славянского языкового родства.-М., 1994.
Крейдлин Г.Е., Шмелев А.Д. Математика помогает лингвистике: Кн. Для учащихся.- М., 1994.
Носенко И.А. Начала статистики для лингвистов.М.,Высшая школа, 1981.
Пиотровский Р.Г.,Бектаев К.Б.,Пиотровская А.А. Математическая лингвистика.-М., Высшая школа, 1977.
Сухотин Б.В. Исследование грамматики числовыми методами.-М., 1990.
Хант ДЖ. Вычислительная лингвистика в Летнем Институте лингвистики//Вопросы языкознания.1993.№6.С.114-125.
Фрумкина Р.М. Сатистические методы изучения лексики.М., Наука, 1964.
10.Лингвистическое моделирование.
В ХХ веке в различных науках, особенное естественно-математического цикла, складывается и эффективно используется методика моделирования.
Подчас наука имеет дело с такими явлениями, которые непосредственно исследователем не наблюдаются и не могут быть восприняты нашими органами чувств. В таких случаях и эффективна методика моделирования, сущность которой сводится к тому, что исследователь на основе определенного количества исходных данных строит модель изучаемого явления, исследует эту модель, получает новые данные, проверяет их, затем включает в число исходных данных и на основе большого количества сведений строит уже более сложную, более совершенную модель. Процесс моделирования, как и процесс познания, бесконечен.
Моделью называется некоторое приближенное или и упрощенное представление о структуре и функциях конкретной исследуемой системы. Необходимо заметить, что модель можно построить только в том случае, если изучаемое явление или предмет поняты нами как система. Иначе это уже не модель, а макет.
Разграничиваются модели:1) физические и мыслительные; 2) функциональные (отражающие только действие объекта) и структурные (отражающие структуру и свойства изучаемой системы), структурная модель в познавательном отношении мощнее функциональной; 3) анализирующие (распознающие и синтезирующие (порождающие, порождающие модели эффективнее распознающих).
Интерес к методике моделирования в языкознании вызвал появление множества моделей языка, дающих представление об определенных закономерностях языковой системы. Строго говоря, все лингвистические модели можно квалифицировать как математические и нематематические. Примерами различных математических моделей в языкознании являются статистико-комбинаторные, теоретико-множественные и трансформационные модели. Модели второго (нематематического) типа строятся в основном в направлении, идущем от наблюдения фактов к раскрытию сущности, т.е. к познанию системы существенных определяющих связей и отношений.
43
Просмотр содержимого документа
«00.»
ТЕМА № 1. РОЛЬ ИНТЕГРАЦИОННЫХ ПРОЦЕССОВ В СМЕНЕ ПАРАДИГМ ЯЗЫКОЗНАНИЯ. МАТЕМАТИЧЕСКАЯ ЛИНГВИСТИКА
1.Гуманитарный потенциал математики. Гуманитарный потенциал математики раскрывается по следующим направлениям:
1.Математика изучает математические модели реальных процессов. Это позволит человеку, владеющему математическим языком, глубже проникнуть в суть реальных процессов, правильно ориентироваться в окружающей действительности.
2.Математика «ум в порядок приводит» (Ломоносов). Известно влияние математики на формирование мышления и личностных черт человека.
3.Человек, формулирующий математическое утверждение и приводящий математическое доказательство, оперирует не обыденной, а предметной речью, строящейся по определенным законам (краткость, четкость, лаконичность, минимизация и т.д.). Предметная речь оказывает существенное влияние и на развитие литературной речи.
4.Изучая математику, человек постоянно осознает свое развитие, «поумнение». Осознанность процесса обучения – один из краеугольных принципов теории развивающего обучения – обучение на достаточно высоком уровне трудности, быстрый тем обучения, приоритет теории, дифференцированный подход к учащимся плюс упомянутый выше принцип осознанности процесса обучения, то нетрудно убедиться, что обучение математике наиболее адекватно соответствует системе этих принципов.
2. Математизация лингвистических дисциплин. В эпоху научно-технической революции математизация охватывает все сферы человеческой деятельности, в том числе и такие, казалось бы, чисто гуманитарные науки как языкознание, проникновение математических методов в лингвистику обусловлено двумя причинами.
Во-первых, развитие языковедческой теории и практики требует введения все более точных и объективных методов для анализа языка и текста. Одновременно использование математических приемов при систематизации, измерении и обобщении лингвистического материала в сочетании с качественной интерпретацией результатов позволяет языковедам глубже проникнуть в тайны построения языка и образования текста.
Во-вторых, все расширяющиеся связи языкознания с другими науками, например, с акустикой, физиологией высшей нервной деятельности, кибернетикой, вычислительной техникой, могут осуществляться только при использовании математического языка, обладающего высокой степенью общности и универсальности для различных отраслей знания.
3. Математическая лингвистика. Связь языка с математикой не была односторонней. Примером использования лингвистических знаний в математике служит создание математической лингвистики. Математическая лингвистика использует метод абстрактно-семиотического моделирования явлений естественных языков и процессов их исследования. Центральными понятиями математической лингвистики являются понятия множества исходных символов (алфавит, словарь) и множества последовательностей (цепочек) символов заданного алфавита (множество словоформ, фраз). Эти основные понятия применяются на каждом уровне языка. Физик Н. Бор писал: «Мы не будем рассматривать чистую математику как отдельную область знания; мы будем считать ее скорее усовершенствованием общего языка…»
Усвоение науками отвлеченных понятий и методов математики расширяет их возможности, способствует открытию новых, более глубоких закономерностей. Первой среди гуманитарных наук на языке математики заговорила лингвистика. Системный характер языка, обобщенный характер его единиц - вот та благодатная почва, на которой стали плодотворно укореняться идеи и методы современной математики. Связь языкознания с математикой наметилась давно. Известный русский математик В.Я.Буняковский писал о необходимости применения математики в области грамматических и этимологических исследований. И.А. Бодуэн де Куртенэ, набрасывая контуры будущего языкознания, непременным условием его развития считал тесную и органическую связь с математикой. «Нужно чаще применять в языкознании количественное, математическое мышление и таким образом приблизить его все более к наукам точным». Перспективные мысли высказаны Бодуэном в статье «Количественность в языковом мышлении». Выдающийся лингвист практически использовал квантитативную методику в исследованиях по фонетике (исчисление альтернаций) и по грамматике (описание типов склонения). Крупнейший теоретик языка Е.Д. Поливанов также писал о точках соприкосновения между математикой и лингвистикой.
Для описания и исследования лингвистических фактов привлекаются различные разделы математики: алгебра, теория множеств, математическая логика, теория информации, теория вероятностей и математическая статистика. В силу этого математическая лингвистика стала развиваться в нескольких направлениях - алгебраическая лингвистика, комбинаторная лингвистика, которая опирается на разделы «неколичественной» математики (теория множеств, математическая логика, теория алгоритмов), и квантитативная лингвистика, которая изучает лингвистические явления с помощью «количественной математики» (математическая статистика, теория вероятностей, теория информации и др.)
Статистически исследуется фонетика, закладываются основы статистического изучения морфемного состава слова и морфологических категорий. В частности установлена связь между числом фонем и средней длиной морфемы, стало известно, что количество фонем отражается на качестве морфем и слов, а количество морфем на качестве слов.
С помощью формально-количественных методов изучается авторский идиостиль. Шире всего количественные методики используются при описании лексического уровня языковой системы. Практическим результатом статистического изучения лексики являются частотные словари, отличающиеся от обычных лингвистических (толковых, орфографических им других) тем, что словарные единицы располагаются в них не только в алфавитном порядке, но и в порядке убывающей частотности.
Характерно, что математические методы обладают следующими возможностями:
делают точными суждения, основанные на количественно-частотных соображениях
указывают на такие обстоятельства функционирования языка и диалекта, которые иными способами не обнаруживаются
позволяют глубже и всесторонне понять причины и результаты языковой эволюции, длительность эволюционных процессов и их хронологию, и даже прогнозировать будущее языковое развитие
расширяют сферу прикладного использования языкознания.
Языкознание по существу занимает среди гуманитарных наук особое место, дав классические образцы научной точности. Так, по мнению ученых, сравнительно-историческое языкознание до сих пор остается примером точного лингвистического исследования. «Нет анализа более точного, чем языковой. В самые смутные вопросы лингвистика нередко вносит математическую прозрачность» (Осетров Е. Живая Древняя Русь. М.,1970, с.23).
Просмотр содержимого документа
«01.»
ТЕМА №2. ЕСТЕСТВЕННЫЙ ЯЗЫК И ЯЗЫК МАТЕМАТИКИ.
НЕЧЕТКОСТЬ ЯЗЫКА И ЕГО ЭЛЕМЕНТОВ
Математика подобно любой науке многомерна. На когнитивном уровне она выступает как мышление, на перцептуальном – как чувствование, на лингвистическом – как язык. Лингвистическое измерение математики заслуживает особого рассмотрения. Дело в том, что лишь благодаря ему математике придается интерсубъективный, общезначимый для всех людей характер. Мышление и чувствование всегда индивидуально. Язык же является достоянием всех.
Как известно, язык – это система условных знаков, принятых в некотором сообществе и обеспечивающая коммуникацию его членов. Язык математики удовлетворяет этому определению. Подобно любому языку он состоит из совокупности высказываний (предложений). Особенность математического языка заключается в том, что в нем широко используются математические символы, объединяемые формулой. Учитывая это, часто говорят, что математика – это язык символов и формул. Впрочем, язык математики не сводится к символьным записям и утверждениям. В любом математическом труде используются такие слова и обороты , заимствованные из естественных языков: «предположим, что…», «и будем исходить из следующих аксиом» и т.п. Но в контексте математики этим словам и оборотам речи придается специфическое значение, которое сопрягается со смыслом формализованных утверждений.
Язык математики – это язык людей, имеющих дело с математическими структурами. В одних случаях речь идет непосредственно об этих структурах, в других на их основе разрешаются те или иные конкретные ситуации.
Язык математики часто сравнивают с естественным языком. При этом, как правило, дается восторженная характеристика одного из них. Следует учитывать, что речь идет о различных языках. В случае математических структур для их описания необходим язык математики; на его фоне естественный язык громоздок и двусмыслен. В житейских ситуациях естественный язык имеет преимущества перед математическим языком и ясно, почему: здесь можно обойтись без детальных знаний о математических структурах. Естественный язык не нуждается в замене математическим языком. Существует другое – не усвоивший язык математики не воспользовался благоприятнейшими возможностями своего личного развития. Самое интересное состоит в том, что в общении друг с другом людям то и дело приходится переходить с естественного языка на язык математики и обратно. С различными переходами связаны также междисциплинарные функции математики.
До тех пор пока исследователь находится в пределах чистой математики, он обходится математическим языком. При этом ему нет нужды обращаться к каким – либо другим языкам. Ситуация редко изменяется, когда строятся так называемые математические модели тех или иных (физических, биологических, социальных и т.п.) явлений. Математические модели строятся из терминов, интерпретированных в конкретную объектную область, являющуюся предметом той или иной конкретной науки. Использование математических моделей переводит чистую математику в прикладную.
Итак, в математике как таковой используется математический язык. В конкретной науке используется язык данной науки (в лингвистике – язык лингвистики, в экономике – язык экономики). В прикладной математике, т.е. в случае математических моделей, используются два языка: математический язык плюс язык конкретной науки.
Как же устроен математический язык? Прежде всего это язык абстрактный, в противоположность нашим конкретным языкам, где каждое слово имеет конкретное значение. Язык математических формул и знаков обладает большей универсальностью и используется во всех сферах человеческой деятельности. Система математических знаков является достоянием всего человечества, она вырабатывалась на протяжении тысячелетий. Математический язык – это результат совершенствования естественного языка по различным направлениям: устранение громоздкости и двусмысленности естественного языка, расширение его выразительных возможностей. Он употребляется как средство выражения математической мысли. Язык в широком смысле – это словарь, грамматика, рассказы, повести, пьесы и романы, написанные на этом языке. Что же в математическом языке является аналогом слов и грамматики, а что – рассказов и повестей? Аналог слов и грамматики – математическая операционная система, а рассказов и прочего – математические модели.
Овладение математическим языком предполагает сознательное усвоение содержания математических понятий, отношений между ними (аксиом, теорем) и умение рационально и грамотно выразить математическую мысль в устной и письменной форме с помощью средств математического языка, а также свободное оперирование математическими знаниями, умениями, навыками на практике.
Овладение математическим языком формирует навыки рационального выражения мысли: последовательность, точность, ясность, лаконичность, выразительность, экономность, информированность. Сознательное и свободное владение математическим языком является условием и средством овладения математической культурой. Преимущества математического языка заключаются в следующем: во-первых, по сравнению с естественным языком он обладает большей точностью, во-вторых, благодаря использованию специальных терминов и формул его способ выражения более краток и более нагляден, чем способ выражения естественного языка.
Из названных выше преимуществ вытекает самое важное: без помощи математического языка такие науки как физика и лингвистика не смогли бы достичь сегодняшнего уровня, потому что человек не в состоянии понять сложные связи этих наук на естественном или специально-научном не символическом языке. Уже перевод относительно простых формул на естественный язык создает иногда такие сложные образования, что они почти непонятны. Поясним это на примере из математики. Для области рациональных чисел действителен так называемых закон коммутативности сложения, выраженный в формуле а+ b=b+a. Словами это было бы выражено так: «Если любое число прибавить ко второму, то сумма будет равна сумме этих же чисел, если бы второе число прибавили к первому». Хотя речь идет об очень простом законе, становится ясно, что с помощью формулы его можно выразить короче, яснее и точнее.
Недостатками математического языка являются его специфичность и ограниченная возможность отображения.
Основные расхождения между естественными и математическим языками связаны с различным построением языкового знака и знака математического.
Во-первых, лингвистический знак (слово, словосочетание, предложение) обычно включает в себя четыре компонента – имя (материальный носитель информации), денотат (отражение предмета из внешнего мира), десигнат (понятие о предмете) и коннотат (комплекс чувственно-оценочных оттенков, связанных с предметом и понятием о нем); знак математического языка включает только имя и десигнат (математическое понятие).
Во-вторых, лингвистический знак многозначен, математический знак имеет, как правило, одно концептуальное значение.
В-третьих, лингвистический знак потенциально метафоричен, у знака математического метафоричность полностью отсутствует.
Все эти свойства лингвистического и математического знаков можно проследить. Сравните значение математического знака 3 и слова тройка. Если 3 имеет единственное десигнативное математическое значение – «3 любых объекта», то слово тройка имеет несколько значений: «цифра три», «оценка в три балла», «упряжка из трех лошадей», «группа из трех человек», «разновидность мужского костюма» ит.п. При этом в значении слова тройка содержатся не только указанные десигнативные понятия, оно может указывать на конкретный предмет, например, на вполне определенный костюм. Одновременно это слово несет дополнительные коннотативные метафорические оттенки, связанные с такими словосочетаниями как «Бог троицу любит», «дохлая тройка», «с третьей попытки» и др.
Из всего сказанного вытекает еще одно важное различие между десигнативными значениями математического и лингвистического знаков.
Значение каждого математического знака можно легко представить в виде множества элементов, причем такое множество имеет вполне четкие границы: значение знака 3 является множеством, охватывающим такие конкретные совокупности, которые включают только три (не пять, не восемь) предметов.
Иначе организовано десигнативное значение лингвистического знака – и оно также может рассматриваться как множество денотатов, однако это множество не всегда имеет четкие границы. Так, например. Не удается определить смысловые границы слов синий и зеленый. Разные люди в зависимости от особенностей своего хроматического зрения будут называть показываемые им конкретные синие оттенки то синим, то зеленым цветом. Также нельзя указать точную временную границу, разделяющую значения слов ночь и утро. Иными словами, значения лингвистических знаков представляют собой нечеткие множества с размытыми границами. Особенности построения лингвистического знака приводят к тому, что естественный язык представляет собой нежестко организованную диффузную систему, которая воспринимается и используется человеком в значительной мере интуитивно.
Основными недостатками естественного языка являются следующие:
1.Слова естественного языка со временем постепенно и почти незаметно меняют свое значение.
2.В естественном языке часто бывает, что одно слово одновременно имеет два или более различных значений и одновременно обозначает различные предметы, но бывает также, что различные слова имеют одно и то же значение, обозначают один и тот же предмет. Слово «церковь» обозначает, например, и здание церкви, и вид религии. Различные слова, например, «превосходство» и «перевес» или «катастрофа» и «катаклизм» имеют одно и то же значение.
3.Значение слов естественного языка часто бывает расплывчатым, неопределенным, т.е. не всегда можно сказать об определенном предмете, что слово обозначает именно его. Часто, например, нельзя сказать о человеке, здоров он или нет. В таком случае помогают себе неопределенной формулировкой: он не совсем здоров.
4. Наконец, употребляемые грамматические правила построения выражений естественного языка в логическом смысле также несовершенны, не в любом случае можно определить, имеет данное предложение смысл или нет.
Напротив, язык математики является хорошо организованной системой, существующей и функционирующей в виде логического построения, каждый элемент которого имеет осознанную значимость.
Конфронтация естественного языка и языка математики требует, чтобы каждому лингвистическому объекту был поставлен в соответствие некоторый математический объект. Лингвистический знак, например, словосочетание или слово и составляющие этот знак фигуры – фонемы, буквы, слоги - должны интерпретироваться с помощью знаков математических. Эта математическая интерпретация связана с расчленением лингвистического объекта и выделением в нем одного смыслового или сигнального компонента, который становится предметом дальнейшего исследования. Остальные сигнальные и смысловые элементы лингвистического объекта исключаются.
Просмотр содержимого документа
«02.»
ТЕМА № 3. ЛИНГВИСТИЧЕСКИЕ МНОЖЕСТВА
Одно из основных понятий современной математики – понятие множества. Данное понятие является первичным, т.е. не поддается определение через другие, более простые понятия. Множество – это набор, совокупность каких-либо объектов, обладающих общим для всех их характеристическим свойством.(Например, множество зданий города Ташкента, множество планет Солнечной системы, множество букв русского или узбекского алфавита ит.д.).«Множество» - это самое широкое по объему понятие математики и математической логики. Само понятие множества и понятие «элемент» (член множества) введены в научный обиход немецким математиком Георгом Кантором (1845-1918).По его словам «множество есть многое, мыслимое нами как единое».Прежде всего, множества состоят из определенного набора объектов, которые называются элементами множества. При этом каждый из объектов данного вида либо принадлежит, либо не принадлежит данному множеству. Так, например буква A принадлежит множеству букв, образующих русский алфавит. В то же время буква А этому множеству не принадлежит. Множества, включающие только такие объекты, принадлежность или непринадлежность которых к тому или иному множеству не вызывает сомнений, называются четкими множествами. Подобные множества всегда имеют ясно очерченные границы. Четким множествам противопоставлены нечеткие или «лингвистические множества». Нечеткие множества включают в себя такие объекты, которые могут быть отнесены к тому или иному множеству лишь с определенной степенью достоверности. Множества, которые состоят из конечного числа элементов, называются конечными множествами. К числу конечных относятся также и пустые множества, которые не содержат ни одного элемента. Например, множество двухбуквенных сочетаний бй, чы, ой можно считать пустым, если иметь в виду только русские тексты. Математика чаще всего имеет дело с конечными множествами объектов, а в лингвистике приходится рассматривать и бесконечные множества. Например, бесконечным является множество всех словоупотреблений в текстах данного языка при условии, что этот язык беспрерывно порождает и будет порождать новые тексты без какого-либо ограничения во времени. То, что мы называем значением слова (а их обычно у слова бывает несколько), можно представить в виде множества семантических элементов. Языковеды называют их семами. Сема – простейшая единица значения, которая выделяется в результате лингвистического анализа. Первым представил значение слова в виде множества датский глоссематик Хьюго Ульдалль. Для этого он использовал нехитрую математическую символику. Например: Мальчик = {человек + мужского пола + несовершеннолетний}.Основными операциями, осуществляемыми над множествами, являются сложение, умножение и вычитание. Эти операции не являются тождественными одноименным арифметическим, производимым над числами.
Объединением или суммой двух множеств называется множество, содержащее все такие и только такие элементы, которые являются элементами хотя бы одного из этих множеств. Объединение множеств в математике записывается так: А + В.Если одни и те же элементы содержатся в обоих множествах, то в сумму А+В эти элементы входят только по одному разу. Например, рассмотрим слова женщина и врач как лингвистические множества, состоящие из семантических элементов. Женщина = {человек + женского пола}. Врач = {человек + имеет медицинское образование + лечит больных}. Сумма данных множеств дает новое понятие «женщина-врач» и состоит из 4 элементов, а не из пяти, как это имело бы место при сложении чисел. Пересечением (или умножением) двух множеств А и В (обозначается АВ) называется множество тех элементов, которые принадлежат и к А , и к В. Обозначим множества семантических элементов, входящих в семантическую группу «Возраст» в1 – несовершеннолетний в2 – молодой в3 – старый.
Новое множество АВ, полученное в результате умножения, называется произведением.
Разностью двух множеств А и В называется множество всех таких элементов множества А, которые не содержатся во множестве В .Разность множеств обозначается А – В. Так, если мы обозначим множество русских гласных {а,о,у,э,и,ы} через В, а множество огубленных гласных {о, у} через А, то В – А = {а,э,и,ы}.
Просмотр содержимого документа
«03.»
ТЕМА № 4. ОТНОШЕНИЯ ФУНКЦИОНАЛЬНОЙ ЗАВИСИМОСТИ
В ГРАММАТИЧЕСКОЙ СИСТЕМЕ
1. Понятие функции в лингвистике. Нам уже не раз приходилось сравнивать различные лингвистические и нелингвистические множества. Сопоставление множеств приводит к понятию соответствия, которое подобно понятию множества является одним из основных понятий математической лингвистики. Рассмотрим вопрос о соответствии множеств на примере одного из звуковых законов в истории русского языка. В древнейшую эпоху действовал закон, по которому согласные Г, К, Х перед гласными переднего образования изменялись в мягкие шипящие Ч, Ж, Ш (явление палатализации): рука – поручити, друг – дружити, сух – сушити. В более поздний период этот закон перестал действовать. Представим согласные Г, К, Х как множество А, а соответствующие им мягкие шипящие Ч, Ж, Ш в виде множества В. Между множествами А и В имеется соответствие, которое описано в истории русского языка как смягчение согласных, или палатализация. Каждому звуку в множестве А соответствует определенный звук в множестве В. При этом переход от звуков множества А к звукам множества В совершается по четко определенному правилу: согласные звуки смягчаются. Если два множества находятся в таком соответствии, что каждому объекту х из множества А ставится в соответствие некоторый определенный объект у из множества В, то говорят, что между А и В существует функциональная зависимость. Правило f , пор которому можно перейти от объекта х Є А к соответствующему ему объекту у Є В, называется функцией. Наш пример со смягчением согласных можно рассматривать как пример лингвистической функции.Для обозначения функции используется запись у = f (х). Если соответствие между двумя множествами установлено, то принято говорить, что на множестве А задана функция со значениями, при -надлежащими множеству В. Объекты х множества А, которым поставлены в соответствие элементы множества В, называются значениями аргумента (или значениями независимой переменной). В нашем случае это согласные Г, К, Х, Все множество А называется множеством значений аргумента, или областью определения (существования) функции f (х). Рассмотрим природу функциональной зависимости в языке на примере типологии предложений по цели высказывания с помощью аппарата математического анализа.По функции заключенного в них высказывания предложения делятся на повествовательные, вопросительные и побудительные. Они служат соответственно для передачи трех основных форм мысли – суждения, вопроса, побуждения. Суждения, требования и вопросы являются отражением объективных связей вещей или явлений. Повествовательные предложения носят информативный, описательный, десигнативный характер. Они дают сведения о прошлом (например, свидетельские показания в суде), о настоящем (например, сведения о магнитном поле Земли) или о будущем (например, в прогнозе погоды). Побудительные предложения носят направляющий, указывающий, предписывающий, определяющий характер, Они побуждают кого-либо к действию или к его прекращению.В форме данных предложений можно сформулировать планы, юридичесие законы и нравственные нормы. Вопросительные предложения выражают желание что-либо узнать. В зависимости от того, хотят ли узнать о том, что есть или было или что надо делать, ответ следует в виде повествовательного или побудительного предложения. Предложения всех трех функциональных типов могут быть эмоционально окрашенными.Повествовательные предложения, в отличие от других типов, не требует ответной реакции адресата:
1.Повествовательное предложение не требует ответной реакции адресата(V1).
2.Побудительное предложение побуждает к действию(V2).
3.Вопросительное предложение требует ответа(V3).
1.V1 – собственно повествовательное предложение. Например, Пришла весна.
1.V2 – повествовательно – побудительные предложения (в ситуации «начальник-подчиненный», «учитель - ученики» и т.п.). Например, Петров идет к доске, Сидоров готовится к ответу.
1.V3 – повествовательно-вопросительные предложения (обычно названия произведений, заголовки статей и т.п.). Например , «Что я видел во сне…»
(рассказ Л.Н.Толстого) «Кому на Руси жить хорошо» (поэма Н.А.Некрасова).
2.V1 – побудительно-повествовательное предложение. Например, Приходи скорей, весна! (Ср.: Хочу, чтобы скорей пришла весна.)
2.V2 – собственно побудительное предложение. Например, Давайте готовиться к приходу весны!
2.V3 - побудительно-вопросительное предложение. Например, Перестанешь ты смеяться, наконец!
3.V1 - вопросительно-повествовательное предложение. Например, Кто из нас заранее не радовался приходу весны? (Ср.: Все мы заранее радуемся приходу весны.)
3.V2 – вопросительно-побудительное предложение. Например, Не подскажете, который час? (Ср.: Подскажите, который час.)
3.V3 – собственно вопросительное предложение. Например, Готовитесь ли вы к приходу весны?
2.Учет обратных функций при обучении языку и переводу. Существование обратных функций в грамматике рассматривается нами как одно из закономерных проявлений противоречивой природы языка, подчиненной основному тезису диалектики: если есть что-нибудь одно, то должно быть нечто иное, противоположное ему. В грамматике любого действующего языка существует ряд явлений, подчиняющихся данной закономерности. Так, например, в морфологии известны случаи контекстного употребления формы изъявительного наклонения глаголов в функции повелительного, например: «Дежурный заболел, а ты его заменишь» (= ты его замени). Здесь налицо функциональная зависимость А → В, где А – изъявительное наклонение , а В – повелительное. Теперь рассмотрим обратную функцию В → А, т.е. употребление формы повелительного наклонения в значении изъявительного, например: «Вот в эту-то Дуняшу и влюбись (влюбился) Аким!» (Тургенев). Для сравнения также приведем пример контекстного употребления формы повелительного наклонения в значении сослагательного (С) – В → С: «Приди ты на час раньше, ничего этого не случилось бы» (= пришел бы ты на час раньше). Обратная функция для данного случая С → В : «Вы бы, доктор, шли спать!» (Чехов). Функция А → С (транспозиция словоформы изъявительного наклонения в семантическую сферу сослагательного): «Ах, какой ты, Федя, ну, послал кого за водкой – и все тут!» (Мамин-Сибиряк) (= ну, послал бы). Обратная функция С → А для данного случая (транспозиция словоформы сослагательного наклонения в семантическую сферу изъявительного) : «Мне хотелось бы поехать» (= я хочу поехать).
При изучении категории времени глагола обратные функции могут быть также рассмотрены аналогичным образом. Обозначим настоящее время глагола как А, прошедшее как В, будущее – С. Задаем функцию
А → В (настоящее – прошедшее): В 1884 г. П.И. Чайковский пишет оперу «Евгений Онегин». Обратная функция (прошедшее – настоящее): Талант и бездарность не уживаются. Там, где восторжествовал талант, бездарности делать нечего (Тендряков). Функция В → С (транспозиция словоформы прошедшего в сферу будущего): Если он не вернется, мы пропали (= мы пропадем). Обратный случай (будущее – прошедшее): Кругом не слышалось почти никакого шума… Лишь изредка в близкой реке с внезапной звучностью плеснет большая рыба, и прибрежный тростник слабо зашумит, едва поколебленный набежавшей волной (Гоголь).
Рассмотрим транспозицию словоформы настоящего времени в сферу будущего (А → С) и обратную ей функцию С → А (будущее → настоящее). Например: Завтра магазин не работает. − Хорошо сидеть и прислушиваться к тишине: то ветер подует и тронет верхушки берез, то лягушка зашелестит в прошлогодней листве, то за стеной колокольни часы пробьют четверть…(Чехов) (= то дует, то трогает, то шелестит, то бьют…).
Просмотр содержимого документа
«04.»
ТЕМА № 5. ОППОЗИЦИЯ, НЕЙТРАЛИЗАЦИЯ И ТРАНСПОЗИЦИЯ КАК УСЛОВИЯ СУЩЕСТВОВАНИЯ И ФУНКЦИОНИРОВАНИЯ ГРАММАТИЧЕСКИХ ЗНАЧЕНИЙ
1. Оппозиция в лингвистике — одно из понятий структурализма: существенное для смыслоразличения различие между единицами плана выражения (например, звуковое противопоставление, которое может дифференцировать значения двух слов). Такому различию соответствует различие единиц плана содержания.
Понятие оппозиции используется для разграничения языковых единиц (инвариантов) и их вариантов: инварианты способны вступать друг с другом в оппозитивные отношения, а варианты не обладают такой способностью (их отношениянеоппозитивны).
Примером оппозиции на фонологическом уровне в русском языке может служить пара заднеязычных согласных фонем /k/ —/x/: они способны быть единственным средством смыслоразличения, например в паре корь — хорь. Напротив, [g] и [ɣ]являются вариантами одной фонемы, поскольку аналогичной пары для них в русском языке нет (более того, эти звуки взаимозаменяемы).
Приверженцы Московской фонологической школы приводят и другой пример: положение школы об отсутствии в русском языке самостоятельных фонем , , аргументируется тем, что названные звуки не образуют смыслоразличительных фонологических оппозиций со своими твёрдыми вариантами [g], [k], [x] и потому являются лишь вариантами фонем , и соответственно.
2. Согласно трактовке Н.С. Трубецкого, нейтрализация понимается как утрата определенным признаком в данной позиции своих различительных функций, хотя в других позициях он является различительным. Например, согласный имеет различительный признак "глухость" - перед гласными, т.к. в той же позиции возможен противоположный признак "звонкость": коса - коза. Однако на конце слова и нейтрализованы, т.к. звонкий в этой позиции невозможен: = и кос, и коз.
Другой тип нейтрализации мы имеем в примерах: Ученый совет тепло встретил выступление заведущего/ заведующей кафедрой Борисовой; Мы ждали, но никто не пришел/ приходил; Когда я пришел в себя, коробка исчезла. Должно быть, ее выбросили санитары/ выбросил санитар. Или сестра. В первом примере представлена нейтрализация по категории рода, во втором - по категории вида, в третьем - по категории числа.
Нейтрализация в морфологии.
Пример 1.Сравним ряды:
видна река видно реку
виден пруд видно пруд
видно озеро видно озеро
Видно озеро в одном ряду - сочетание именительного падежа с кратким прилагательным, двусоставное предложение. В другом ряду - это безличное предложение с предикативным наречием, а озеро - дополнение в винительном падеже.
Отдельно взятое предложение Видно озеро одновременно и двусоставное, и односоставное безличное; слово озеро в нём стоит одновременно и в винительном, и в именительном падеже.
Пример 2.В сочетаниях типа быстро бежит, зорко видит, тихо поёт слова на -о можно рассматривать как форму прилагательного в позиции "при глаголе", т.к. такая форма на -о соотносится с качественным прилагательным в его полных формах, оно образовано от прилагательного. С другой стороны, такие слова полностью отвечают сути наречия: это неизменяемые слова, которые назначены обстоятельственно обслуживать глаголы. Следовательно, в этих формах на -o нейтрализованы прилагательные и наречия.
Пример 3.При количественных числительных в именительном-винительном падежах существительное должно находится в родительном падеже; при словах два, три, четыре - в форме единственного числа, при словах пять, шесть и далее - в форме множественного. Число и падеж здесь нейтрализованы: раз выбор числа и падежа исключен, значит, нет и оппозиции; нет оппозиции - нет значения.
Пример 4.В сочетаниях типа посещения больных, переводы Тютчева, поиски экспедиции скрывается два значения: Тютчев переводит и Тютчева переводят. В этих сочетаниях нейтрализованы два значения родительного падежа: субъект действия и объект действия.
3.Транспозиция, в противоположность нейтрализации, явление исключительно распространенное, продуктивное и регулярнoe в грамматике. Она охватывает все случаи переносного использования грамматических значений. Транспозиция частей речи, лексико - грамматических разрядов, словоформ пределах именных и глагольных категорий, синтаксических форм и конструкции разных типов - вот только некоторые наиболее известные случаи транспозиции в грамматике. В подтверждение сказанного приведем примеры транспозиции на разных уровнях грамматической семантики (без описания) (Ким, I978,1984,1986). Ср.: Пусть его идет (= Пусть он идет); Пусть ее погуляет 1 (= пусть сна погуляет); Пусть их шумят (=Пусть они шумят); У Печориных есть воля без знания, у Рудиных знание без воли; у Базаровых есть и знание и воля. Мысль и дело сливаются в одно целое (Писарев); Бескорыстный, простодушный, беззащитный перед железной силой так вот знающих сное дело виталиков, он как бы являет coбой светлый лик страждущей доброты, вопиющей о попутанной чистоте и красоте земной... (Закжевская). Не исчезла тень Пилата, всесильного наместника империи, и по ceй день (Ведь есть потенциальные пилаты и теперь) (Айтматов). Подкинули-таки! - со злобой процедил он сквозь зубы, сжимая кулаки. - Вот оно лежит... лежит беззаконие! (Чехов). А как он плохо подумал об этом враче поначалу. Писателем себя вообразил. Отгадчиком человеческих душ. Вот и доверяй первому впечатлению (= Нельзя доверять/не доверяй первому впечатлению) (Якименко). Я вышел, посмотрел. Паровоз чернеет (= чернел) так далеко впереди, что едва виден (= был виден). С подножек поезда соскакивают (= соскакивали) люди с чайниками в руках - спешат (спешили) в буфет за кипятком (Бунин). Привиделась мне однажды странная картинка... Сохлый дуб... а я будто на всю деревню... Сижу (= сидел), распеваю (= распевал), как на дождь, а страх исходит (= исходил) лишь от неизвестности (Семенов). Лыковская жизнь его (Чижегова) кончалась. Кроме Киры в ней бита и эти люди, они любили его. До этого вечера он как - то не думал об этом. Он лишается (= лишился) их, он расстается (= расставался) с друзьями, и, кто знает, стоит (= стоила) ли вся его придумка с регулятором этой потери (Гранин).
Приведенные примеры подобраны не только для иллюстрации транспозиционных возможностей оппозиционного механизма грамматики русского языка. Они показывают "жизнь" грамматического значения в тексте, в которую вовлечены все компоненты языковой семантики в их сложном взаимодействии.
Можно указать еще на следующие признаки различии нейтролизации и транспозиции: а) в отличие от транспозиции нейтрализация в стилистическом отношении всегда беспризнакова; б) транспозиция более характерна для сильного члена оппозиции, а нейтрализация - для слабого.
Просмотр содержимого документа
«05.»
ТЕМА №6. ТИПЫ ТРАНСПОЗИЦИИ НА УРОВНЕ ЧАСТЕЙ РЕЧИ
1.Семантические основания частей речи и транспозиция.
2.Транспозиция частей речи.
3. Типы ТЧР в современном русском языке.
1. Для изучения семантического механизма транспозиции на уровне частей речи языка релевантна категоризация словарного состава по обобщенным значениям, характеризующим все слева того иного класса. Являсь обобщением значений слов всей частей речи, (категориальные) значения представляют собой семантическую категорию наиболее высокой степени абстракции, включающую в себя все частные морфологические значения в пределах той или иной части речи.
Классификация слов современного русского языка, основанная на категориальной семантике, позволяет выделить следующие семантические классы (СК); существительные, прилагательные, числительные, глагол, инфинитив, причастие, деепричастие, наречие, категория состояния, союз, предлог, частица, модальные слова, междометие.
Категориальные значения выделенных СК представляют собой определенную систему, а основе которой ПРЕДМЕТ, ПРИЗНАК и ОТНОШЕНИЯ, противопоставленные и связанные иедде собой каким - нибудь дифференциальным признаком.
Грамматический ПРЕДМЕТ - любой предмет речи, все то, о чем можно говорить (вещи, явления, свойства, существа к т.п.). ПРИЗНАК - все то, в чем предметы сходны друг с другом, в чем они отличаются друг от друга. ОТНОШЕНИЕ - форма взаимосвязи между предметами между, различными признаками.
Существительное, называя предмет, противопоставляется всем остальным полнозначным словам, обозначающим различные признаки. Последние делятся на слова, обозначающие непроцессуальный признак, и на слова, обозначающие процессуальный признак. К первым относятся прилагательные, числительные, категория состояния, наречия, ко вторым - глагол, инфинитив, причастие, деепричастие. По отношению к предмету каждая из этих двух групп делится на слова, обозначающие признак объекта, и на слова, обозначающие признак не объекта. На этом уровне выделяется наречие, обозначающее непроцессуальный признак не объекта (признак признака).
Слова, выражающие отношение, могут быть разбиты на две группы: I) слова, выражающие синтагматические отношения; 2) слова, выражающие несентагматические отношения. К первой группе относятся союзы и предлоги, ко второй - частицы, модальные слова и междометия.
Союзы и предлоги различаются между собой тем, что предлог выражает различные синтагматические отношения гетерокатегориального характера, а союз, который всегда связывает однородные (однокатегориальные) элементы - члены предложения, части сложного предложения, может быть охарактеризован как выразитель негетерокатегориальных синтагматических отношений.
Частицы как слова, вносящие различные добавочные оттенки в значения отдельных слов или предложений, не осуществляют связующей функции в конструкции. Они являются выразителями различных несинтагматических коннотативных отношений эмоционально - оценочных и смысловых.
Модальные слова и междометия не выражают коннотативных отношений. Модальные слова - это средство описательного выражения модальности в языке. Обозначим категориональные семы их через модальные несинтагматические отношения, М е ж д о м е т и я, как выразители различного рода эмоций и волеизъявлений, могут быть охарактеризованы как слова немодальных неконнотативных несинтагматических отношений.
Особым образом выделяются мест о и м е н и я. Они отличаются от других знамечательных слов только способом представления реальной действительности в языке, не имея, однако, своего "кусочка" представления. В противоположность словам - названиям, "значение которых носит абсолютный характер в том смысле, что оно детерминировано реальной действительностью", местоимения выделяют и дифференцируют факты, явления, предмета и лица, не называя их, а лишь указывая на них, уже названных другими словами. Значение местоимений носит относительный характер, оно зависит от "координат речевого акта", от контекста. Как слова - указания (дидактические), местоимения в зависимости от того, на что они указывают, могут классифицироваться только как местоимения - существительные, местоимения - прилагательные, местоимения числительные, местоимения-наречия.
2.Семантической основoй частей речи обусловлено явление транспозиции на уровне частей речи - порождение вторичных КЗ в процессе функционивания слов разных частей речи.
Явление ТЧР связано не с морфологической спецификой части речи - не с ее парадигматической схемой и даже не с системой морфологических категорий, - а с ее поведением в высказывании в качестве семантического компонента. Отсюда для выяснения и описания механизма ТЧР определяющими, существенными признаками в части речи являются ее категориальное значение и функции этого значения "в процессе сложения смыслов" внутри единицы следующего по высоте уровня.
Механизм TЧP состоит в обмене функциями между элементами функционально и семантически противоположных классов и установлении асимметричных отношений между КЗ и функцией. Другими словами, ТЧР - это перенос, слова или словоформы той или иной части речи в сферу КЗ и функций другой части речи.
Русский язык с его богатой системой аффиксальной деривации реализует далеко не все теоретические возможные типы ТЧР.
3.Типы ТЧР в современном русском языке. По принципу принадлежности транспозита к тому или иному СК выделяются следующие типы ТЧР:
Отсубстантивная транспозиция, при которой в качестве транспозита выступает имя существительное.
Отадьективная транспозиция, при которой в качество транспозита выступает имя прилагательное.
Отглагольная транспозиция, при которой и качестве транспозита. выступает глагол и личной форме.
Отдепричастная транспозиция, при которой в качестве транспозита, выступает причастие.
Отдеопричастная транспозиция, при которой в качестве транспозита выступает деепричастие.
Отнаречная транспозиция, при которой в качества транспозита вступает наречие.
Просмотр содержимого документа
«06.»
ТЕМА №7. ПОНЯТИЕ О ФУНКЦИОНАЛЬНО-СЕМАНТИЧЕСКОМ ПОЛЕ
Функциональная грамматика основывается на теории функционально-семантических полей. Функционально-семантическое поле – это система разноуровневых средств данного языка (морфологических, синтаксических, словообразовательных, лексических, а также комбинированных – лексико-синтаксических и т.п.), взаимодействующих на основе общности их функций, базирующихся на определенных семантических категориях. ФСП аспектуальности, темпоральности, залоговости, локативности и т.п. представляют собой разновидности языковых категорий. Функционально-семантические поля включают не только грамматические единицы, классы и категории как исходные системы, но и относящиеся к той же системе семантической категории элементы их среды. Термин «ФСП» связан с представлением о группировке (упорядоченном множестве) взаимодействующих языковых средств и их системно-структурной организации. Понятие «функционально-семантическое поле» включается в систему понятий и терминов грамматики, исследующей языковые единицы не только в направлении от формы к значению, но и от значения к форме.
В основе каждого функционально-семантического поля лежит определенная семантическая категория – тот семантический инвариант, который объединяет разнородовые языковые средства и обуславливает их взаимодействие. ФСП представляет собой двустороннее (содержательно-формальное) единство, охватывающее конкретные средства данного языка со всеми особенностями их формы и содержания.
Для структуры ФСП характерно соотношение центра и периферии. Ядром (центром) ФСП является единица языка, наиболее специализированная для выражения данной семантической категории. Понятия центра и периферии ФСП связаны с более общей идеей центра и периферии в системе языка (Ф.Данеш и др.).
Ядром ФСП аспектуальности является грамматическая категория вида, объективной модальности – грамматическая категория наклонения, компаративности – грамматическая категория степеней сравнения, темпоральности – категория времени, диатезы – категория залога, пола – категория рода, семантической роли – категория падежа, персональности - категория лица. количества – категория числа и т.п.
Грамматическим ядром ФСП не обязательно должна быть грамматическая категория. Например, ФСП разного рода обстоятельственных отношений (причины, цели, условия, уступки, следствия, места) не имеют в русском языке центрального морфологического стержня.
Описание системы ФСП того или иного языка может рассматриваться как одна из задач функциональной грамматики.
Просмотр содержимого документа
«08.»
ТЕМА №9. КОМБИНАТОРНЫЙ ПОДХОД К ОПРЕДЕЛЕНИЮ ИНФОРМАЦИИ
1.Что такое информация. 2.Подходы к измерению информации в языке
1. Информация (от лат. Informatio - разъяснение, изложение, осведомление производная от лат. informare - придавать форму) - совокупность каких либо сведений, данных, передаваемых людьми устно (в форме речи), письменно (в виде текста, рисунков, таблиц, чертежей, условных обозначений) либо другим способом (например, с помощью световых и звуковых сигналов, электрических и нервных импульсов и т.д.) [1]. 2.Под информацией в быту (житейский аспект) понимают сведения об окружающем мире и протекающих в нем процессах, воспринимаемые человеком или специальными устройствами. 3.Под информацией в документалистике понимают все то, что так или иначе зафиксировано в знаковой форме в виде документов.
4.Под информацией понимают сведения, обладающие новизной. 5.Информация – это отражение внешнего мира с помощью знаков.
Ещё одно определение: информация (в широком смысле) - абстрактное понятие, имеющее множество значений, в зависимости от контекста. Пожалуй, это самое простое определение информации, эквивалентное тому, что «мы знаем, что ничего не знаем» и косвенно свидетельствующее о том, что информация - это форма без содержания. Информация в смысле значения языковой единицы означает окружение языковой единицы. В языкознании, дистрибу́ция (позиционное распределение) — это множество всех окружений (контекстов), в которых встречается некоторый элемент, то есть множество всех (различных) возможных позиций элемента относительно позиций других элементов. Дистрибутивность (лат. слово distributivus – «распределительный»)- распределительный закон, связывающий сложение и умножение чисел. Термин ввел франц. математик Ф. Сервуа (1815 г).
2. Подходы к измерению информации. 1. Комбинаторный подход. Вполне естественным является чисто комбинаторный подход к понятию «энтропии речи», если иметь в виду оценку «гибкости» речи - показателя разветвленности возможностей продолжения речи при данном словаре и данных правилах построения фраз.
2. Структурный подход. Измеряет количество информации простым подсчётом информационных элементов, составляющих сообщение. В рамках структурного подхода выделяют три меры информации: 1) геометрическая – определяет максимально возможное количество информации в заданных объемах. Единицей измерения является информационный элемент. В этом случае в качестве информационного элемента выступает минимальная единица хранения – бит; 2) комбинаторная – оценивает возможность представления информации при помощи различных комбинаций информационных элементов в заданном объёме. 3) аддитивная – эта мера предложена в 1928 г. американским учёным Хартли, поэтому имеет второе название – мера Хартли. Единицей измерения информации в аддитивной мере является бит.
3. Статистический подход. Учитывает вероятность появления сообщений: более информативным считается то сообщение, которое менее вероятно, т. е. менее всего ожидалось. Применяется при оценке значимости получаемой информации.
4. Семантический подход. Учитывает целесообразность и полезность информации. Применяется при оценке эффективности получаемой информации и её соответствия реальности.
5. Вероятностный подход. Рассмотрим пример. Допустим, нужно угадать одно число из набора чисел от единицы до ста. По формуле Хартли можно вычислить, какое количество информации для этого требуется: I = log2 100 = 6,644. Таким образом, сообщение о верно угаданном числе содержит количество информации, приблизительно равное 6,644 единицы информации.
6. Алфавитный подход. Количество информации, содержащейся в последовательности символов, определяется минимально возможным количеством двоичных знаков, необходимых для кодирования этой последовательности безотносительно к содержанию представленного ею сообщения. При этом для кодирования наиболее часто используется двоичный алфавит, состоящий из нуля и единицы, это так называемое двоичное кодирование информации.
Полезное для учителя























