Математические задачи в прозе и поэзии: очевидное и невероятное

Общешкольный конкурс проектов и исследовательских работ

МАОУ «Савинская средняя школа»

Математические задачи в прозе и поэзии:

очевидное и невероятное

Авторы:

Ученицы 8 класса

Очелдиева Нигина, Ширкалина Анастасия

Руководитель: Полякова Елена Ивановна

учитель математики

Д.Ванюки

2014

Введение

«…Нельзя быть математиком,

не будучи в тоже время и поэтом в душе»

С.Ковалевская

Литература и математика - что может объединять эти далекие друг от друга области знаний? Сочетать несочетаемое - привычная работа нашего воображения, когда мы ищем объяснение непонятному.

Хорошие книги можно читать по–разному:«залпом», едва поспевая за увлекательно разворачивающимся сюжетом, или медленно, наслаждаясь красотой авторского слога. А еще можно читать глазами математика, замечая и анализируя забавные ситуации. И это не только увлекательное, но и поучительное занятие.

Цель исследования – поиск математических задач в литературе и поэзии, их решение и анализ.

Задачи:

1. Определение цели работы.

2. Подбор художественной, научно – популярной, занимательной литературы для исследования.

3. Систематизация и анализ собранного материала по теме.

4. Решение задач и оценка полученных результатов.

5. Проведение мониторинга по решению задачи.

6. Создание презентации.

7. Оформление работы.

Оглавление

Введение

Глава I. Решение задач

1.1 Задачи, решенные авторами произведений

1.2 Достоверные математические сюжеты в произведениях

1.3 Невероятные математические сюжеты в произведениях

1.4 Задачи, предложенные авторами без решения

1.5 Составление математических задач по литературным сюжетам

Заключение

Библиографический список

Задачи, решенные авторами произведений

• Жуль Верн о скале
• О путешествии вокруг земли
• Толстой задача из арифметики

Герои Жюля Верна

Сегодня нам надо измерить высоту площадки Дальнего вида, сказал инженер. Вам понадобится для этого инструмент? – спросил Герберт. Нет, не понадобится. Мы будем действовать несколько иначе, обратившись к не менее простому и точному способу. Взяв прямой шест, футов 12 длиной, инженер измерил его возможно точнее, сравнивая со своим ростом, который был ему хорошо известен. Герберт же нёс за ним отвес: просто камень, привязанный к концу верёвки.

Не доходя футов 500 до гранитной стены, поднимавшейся отвесно, инженер воткнул шест фута на два в песок и, прочно укрепив его, поставил вертикально с помощью отвеса. Затем он отошёл от шеста на такое расстояние, чтобы лёжа на песке, можно было на одной прямой линии видеть и конец шеста, и край гребня. Эту точку он тщательно пометил колышком. – Тебе знакомы зачатки геометрии? – спросил он Герберта, поднимаясь с земли. – Да.                                                                                                                  – Помнишь свойства подобных треугольников? – Их сходные стороны пропорциональны.

– … Если мы измерим два расстояния: расстояние от колышка до основания шеста и расстояние от колышка до основания стены, то, зная высоту шеста, сможем вычислить четвёртый, неизвестный член пропорции, т. е. высоту стены.

Оба горизонтальных расстояния были измерены: меньшее равнялось 15 футам, большее – 500 футам. По окончании измерений инженер составил следующую запись:

15 : 500 = 10 :  х; 500 х 10 = 5000; 5000 : 15 = 333,3.

Значит, высота гранитной стены равнялась 333 футам.

Задача Л. Н. Толстого

Условие задачи: Мужик продает шапку. За шапку хочет 10 рублей. Подходит покупатель, смотрит, меряет и решает купить. Дает 25 рублей одной купюрой. У продавца нет сдачи. Он посылает мальчишку-помощника к тете Клаве разменять деньги. Мальчишка деньги быстренько разменял и вернулся. Мужик отдал покупателю шапку, сдачу и тот ушел. Через некоторое время прибегает тетя Клава и заявляет, что деньги, которые принес на размен мальчишка фальшивые. Она предлагает мужику не ходить в участок, а прямо сразу вернуть ей деньги. Делать нечего, мужик лезет в карман и отдает тете Клаве свои кровные 25 рублей.

Вопрос: На сколько денег «попал» продавец?

Решение: Итак, мужик получил деньги только от тети Клавы, которая в результате размена вручила ему через мальчика 25 рублей. А выплачивал он деньги дважды - это сдача покупателю шапки (15 рублей) и возврат тете Клаве 25 рублей вместо фальшивых. В сумме - 40. Разница 40 – 25 = 15.

Ответ: 15 рублей.

Приложение

Результаты мониторинга по решению задачи Л.Н.Толстого среди учащихся МАОУ СОШ №1 .

класс

Количество учащихся

6Б

Решивших правильно

7 Б

25

7В

Процент выполнения

19

8

9 В

5

19

32%

26%

11 Б

2

19

итого

10,5%

5

26

26%

3

108

11,5%

23

21,3%

Достоверные математические сюжеты в произведениях

• Тургенев «Му-Му»
• Некрасов «Дед Мазай и зайцы»
• Крылов «Лебедь Щука и Рак»
• Геометрия Гулливера

Повесть Тургенева И.С. « Му-му»

Говоря о каком – то персонаже, писатели нередко указывали его рост. «…Из числа всей ее челяди самым замечательным лицом был дворник Герасим, мужчина двенадцати вершков роста, сложенный богатырем и глухонемой от рождения».

Зная соотношения между старорусскими мерами длины и современными (1 вершок = 4,5 см) вычислим рост Герасима.

12 ∙ 4,5 см = 54 см.

И что же мы получили? Рост младенца в среднем составляет 51-53 см. Какой же Герасим тогда богатырь?

Может писатель ошибся, или мы неверно представляем себе указанные автором величины?

Оказывается раньше, говоря о росте взрослого человека, указывали лишь число вершков, на которое он превышал два аршина (1аршин=16вершкам)

Проведем повторное вычисление:

2 ∙ 72см = 144см (это 2 аршина)

144 +54 = 198см (2 аршина и 12 вершков).

Значит, рост Герасима был 1м 98см, а это действительно высокий человек

Н.А. Некрасов « Дед Мазай и зайцы»

Герой стихотворения вспоминает о том, как в полноводье спасал зайцев:

«Вижу один островок небольшой-

Зайцы на нем собралися гурьбой.

С каждой минутой вода подбиралась

К бедным зверькам; уж под ними осталось

Меньше аршина земли в ширину, Меньше сажени в длину».

Каковы же размеры островка в современных единицах длины и площади?

Примем форму острова условно за прямоугольник. Площадь прямоугольника найдем по формуле S = a ∙ b, где

а = 1 аршин = 72см, b = 1 сажень = 216см.

S = 0,72 ∙ 2,16 = 1,5552(кв. м).

Вывод: островок и в самом деле был небольшим

Сюжет из басни И.А.Крылова «ЛЕБЕДЬ, ЩУКА И РАК»

Когда в товарищах согласья нет,

На лад их дело не пойдет,

И выйдет из него не дело, только мука.

Однажды Лебедь, Рак и Щука

Везти с поклажей воз взялись

Когда в товарищах согласья нет,

И вместе трое все в него впряглись;

Из кожи лезут вон, а возу все нет ходу!

Поклажа бы для них казалась и легка:

Да Лебедь рвется в облака,

Рак пятится назад, а Щука тянет в воду.

Кто виноват из них, кто прав - судить не нам;

Да только воз и ныне там.

Решение:

Сложение векторов движения лебедя и щуки выполним по правилу параллелограмма. Диагональ параллелограмма будет суммой двух векторов. Вектор движения рака будет направлен в противоположную сторону, значит, сумма этих векторов будет равна 0. Поэтому «воз и ныне там»!

Геометрия Гулливера

В стране лилипутов футу соответствовал дюйм, а в стране великанов, наоборот, дюйму – фут. Другими словами, у лилипутов все люди, все вещи, все произведения природы в 12 раз меньше нормальных, у великанов – во столько же раз больше. Эти, на первый взгляд, простые отношения сильно усложнялись, когда приходилось решать следующие вопросы:

• Во сколько раз Гулливер съедал за обедом больше, чем лилипут?
• Во сколько раз Гулливеру требовалось больше сукна на костюм, нежели лилипуту и сколько для этого понадобиться портных?
• Сколько весило яблоко в стране великанов?

Лилипуты, читаем мы в «Путешествии», установили для Гулливера следующую норму отпуска продуктов: «Ему будет ежедневно выдаваться столько съестных припасов, сколько достаточно для прокормления 1724 подданных страны лилипутов».

Или: «Ко мне было прикомандировано 300 портных-лилипутов с наказом сшить мне полную пару платья по местным образцам».

А в стране великанов Свифт описывает следующий случай: «…град яблок, каждый величиной с хороший бочонок, шумно посыпался на землю; одно ударило меня в спину и сбило с ног…»

Автор «Путешествия» справился с этими задачами в большинстве случаев вполне успешно. Он правильно рассчитал, что раз лилипут ростом меньше Гулливера в 12 раз, то объём его тела меньше в 12 х 12 х 12 = 1728 раз.

Следовательно, для насыщения тела Гулливера нужно в 1728 раз больше пищи, чем для лилипута (у Свифта ошибочно указано число 1724) Правильно рассчитал Свифт и количество материала на костюм Гулливеру. Поверхность его тела больше, чем у лилипута в 12 * 12 = 144 раза;

Во столько же раз на костюм Гулливера должно было пойти больше сукна, чем на костюм лилипута? Значит, и рабочего времени потребуется больше. Если один портной шьет костюм за 2 дня, то, чтобы сшить за один день 144 костюма (или один костюм для Гулливера), могло понадобиться около 300 портных.

Легко рассчитать и вес яблока в стране великанов. Вес среднего яблока составляет около четверти фута, а в стране великанов оно будет весить в 1728 раз больше, т.е. 432 фута, или почти 11 пудов (176 кг). Такое яблоко, ударив человека в спину, может даже убить его, так что Гулливеру ещё повезло. Надобность производить подобные расчёты возникала у Свифта чуть не на каждой странице. И, вообще говоря, он выполнял их правильно. Если у А.С. Пушкина в «Евгении Онегине», как утверждает поэт, «время рассчитано по календарю», то в «Путешествиях» Свифта все размеры согласованы с правилами геометрии. Лишь изредка надлежащий масштаб не выдерживался.

Невероятные математические сюжеты в произведениях

• Сказания о потопе
• Ошибка Джека Лондона
• Холм Пушкина
• Башня Гоголя

Сказание о потопе

«Через семь дней, - говорится в Библии¸ - воды потопа пришли на землю… И лился на землю дождь 40 дней и 40 ночей… И усилилась вода на земле, так что покрылись все высокие горы, какие есть под всем небом; на 15 локтей поднялась над ними вода… Истребилось всякое существо, которое было на поверхности всей земли. Остался только Ноя и что было с ним в ковчеге». Вода стояла ещё 110 суток; после этого она исчезла, и Ной со всеми спасенными животными покинул ковчег, чтобы вновь заселить опустошенную Землю.

По поводу этого сказания поставим 2 вопроса:

• Возможен ли был такой ливень?
• Мог ли Ноев ковчег вместить все виды наземных животных?

1. Откуда могла взяться вода, выпавшая с дождем потопа? Только из атмосферы. Куда же она девалась потом? Целый мировой океан воды не мог всосаться в почву и как-то покинуть нашу планету. Вода могла только испариться в атмосферу. Там эта вода должна находить и теперь, что могло бы вызвать новый потоп. Проверим это.

Из справочной литературы можно узнать, сколько влаги содержится в земной атмосфере:

- на 1 кв. м опирается столб воздуха, который содержит в среднем около 16 кг водяного пара и никогда не может содержать больше 25 кг.

- 25 кг = 25000г воды занимают V = 25 000 куб.см - площадь поверхности в 1 кв.м составляет 100 * 100 = 10 000 кв.см.

Найдем толщину водяного слоя: V / S = 25 000 / 10 000 = 2,5 см. И это при условии, что вода не впитывается!

Сделанный нами расчет показывает, какова могла быть высота воды при потопе, если бы такое бедствие действительно произошло. Так как высота величайшей горы Эверест примерно 9 км или 900 000 см, то высота потопа преувеличена библией в 90 000 / 2,5 = 360 000 раз! Осенний мелкий дождь дает воды в 20 раз больше.

2. Возможно ли построить Ноев ковчег и разместить в нем все виды наземных животных?

Вычислим площадь ковчега высотой в 3 этажа следующих размеров:

- длина – 300 локтей или 135 метров (« локоть примерно 45 см);

- ширина - 50 локтей или 22,5 метра;

- площадь одного этажа составит 135 * 22,5 = 3040 кв.м;

- площадь всего ковчега - 3040 * 3 = 9120 кв.м.

Число различных видов наземных млекопитающих равно около 3500. Животные брались парами, для них нужен был корм на 150 суток. Для хищников – живой корм, который тоже нужно было кормить.

В ковчеге в среднем на каждую пару животных приходилось всего лишь по 9120 / 3500 = 2,6 кв.м. Но для корма тоже требовалось место.

Такая «живая норма» явно не достаточна, так как где-то должна была разместиться семья самого Ноя, и помимо млекопитающих ковчег должен был дать приют другим видам наземных животных. А это:

- птицы 13 000 видов

- пресмыкающиеся 3 500

- земноводные 1 400

- паукообразные 16 000

- насекомые 360 000 видов

Понятно, что ковчег был недостаточно велик для того. Чтобы исполнить назначение, приписываемое ему библейским сказанием.

Ошибка Джека Лондона

В романе Джека Лондона «Маленькая хозяйка большого дома» даётся следующий материал для геометрического расчёта:

«Посреди поля возвышался стальной шест, врытый глубоко в землю. С верхушки шеста к краю поля тянулся трос, прикреплённый к трактору. Механики нажали рычаг – и мотор заработал. Машина сама двинулась вперёд, описывая окружность вокруг шеста, служившего его центром.

– Чтобы окончательно усовершенствовать машину, – сказал Грэхем, – вам остаётся превратить окружность, которую она описывает, в квадрат.

– Да, при такой системе часть земли на квадратном поле пропадает.

Грэхем произвёл некоторые вычисления, затем заметил:

– Теряется примерно три акра на каждые десять.

– Не меньше».

Расчёт неверен, докажем это. Пусть а  – сторона квадрата. Площадь такого квадрата

Диаметр вписанного круга равен также а , а его площадь .

Пропадающая часть квадратного участка составляет:

Видно, что необработанная часть квадратного поля составляет не 30%, как полагали герои американского романиста, а только 22%

Холм Пушкина

В «Скупом рыцаре» А.С.Пушкин описывает старинную легенду восточных народов:

«Читал я где-то,

Что царь однажды воинам своим

Велел снести земли по горсти в кучу,

И гордый холм возвысился – и царь

Мог с вышины с весельем озирать

И дол, покрытый белыми шатрами,

И море, где бежали корабли»

Это одна из немногих легенд, в которой при кажущемся правдоподобии нет и зерна правды. Можно доказать геометрически, что если бы какой-нибудь древний деспот вздумал осуществить такую затею, он был бы обескуражен мизерностью результата. Перед ним высилась бы настолько жалкая куча земли, что никакая фантазия не смогла бы раздуть ее в легендарный «гордый холм».

Сделаем примерный расчет. Войско в 100 000 воинов считалось очень внушительным. Значит, холм насыпан из 100 000 горстей. Пусть горсть древнего воина равна: 1 горсть ≈ 1/5 литра ≈ 0,2 куб.дм.

Отсюда, объем холма V = 0, 2 * 100 000 = 20 000куб.дм = 20 куб.м.

Холм представляет собой конус, объем которого равен 20 куб.м. Определим высоту этого конуса.

Угол откоса, т.е. угол между образующей конуса и его основанием, равен 45 градусов. В случае более крутого склона земля начнет осыпаться.

Значит, треугольник SOA – равнобедренный и Н = R.

Объём конуса находим по формуле:

V=1/3 πR Н

V=1/3 πН

Н=

Н= =2,4 м

Сомнительно, что с холма такой высоты можно обозревать всё то, о чем мечтал древний деспот

Башня Гоголя

Часто писатели, описывая то или иное событие, не подвергают свои творческие вымыслы математической строгости выводов.

Например, Гоголь в статье ”Об архитектуре нашего времени“ пишет: “башни огромные, колоссальные, необходимые в городе… У нас обыкновенно ограничиваются высотой, дающей возможность оглядеть один только город, между тем как для столицы необходимо видеть, по крайней мере, на полтораста верст во все стороны, и для этого может быть, один только или два этажа лишних – и всё изменится. Объём кругозора по мере возвышения распространяется необыкновенною прогрессией…”

Так ли это в действительности?

Решение :

I. Обозначим дальность горизонта через , высоту значения – h, радиус земли –R

Мы знаем правило: произведение отрезков секущей окружности равно квадрату отрезка касательной, проведённой из одной той же точки.

Значит, ,

α = = 10 , то есть горизонт отодвигается только в 10 раз ; б) h= 1000 h = α = ≈ 31 - примерно в 31 раз Вывод: Дальность горизонта растёт медленнее, чем высота поднятия. Так если к 8-этажному дому пристроить ещё 2 этажа, то дальность горизонта возрастет в раз, то есть в 1,1 раза – всего на 10% Поэтому утверждение “один только или 2 этажа,- и всё изменится “неверно. Такая прибавка мало ощутима . " width="640"

3) Если высота здания будет увеличиваться , то ситуация изменится следующим образом :

а) h = 100 h = α = = 10 , то есть горизонт отодвигается только в 10 раз ;

б) h= 1000 h = α = ≈ 31 - примерно в 31 раз

Вывод:

Дальность горизонта растёт медленнее, чем высота поднятия. Так если к 8-этажному дому пристроить ещё 2 этажа, то дальность горизонта возрастет в раз, то есть в 1,1 раза – всего на 10%

Поэтому утверждение “один только или 2 этажа,- и всё изменится “неверно.

Такая прибавка мало ощутима .

• Рассмотрим идею сооружения башни, с которой можно было бы видеть, “ по крайней мере, на полтора вёрст”, тоесть примерно на 160 км.

• α = , R 3 ≈ 6400 км

160 = 25600 = 2Rh

h = = 2(км)

Это высота большой горы!!!

Вывод:

Зданий такой высоты нет и в наше время. А во времена Н.В Гоголя даже Эйфевелевой башни (высотой 300м) еще не существовало. Идея Гоголя несбыточна .

Задачи, предложенные авторами без решения

• Возраст Диофанта
• Задача о лотосе
• Задача про пчёл
• Задачи из 1001 ночь

Возраст Диофанта

Прах Диофанта гробница покоит; дивись ей - и камень

Мудрым искусством его скажет усопшего век.

Волей богов шестую часть жизни он прожил ребенком.

И половину шестой встретил с пушком на щеках.

Только минула седьмая, с подругою он обручился.

С нею пять лет проведя, сына дождался мудрец;

Только полжизни отцовской возлюбленный сын его прожил.

Отнят он был у отца ранней могилой своей.

Дважды два года родитель оплакивал тяжкое горе,

Тут и увидел предел жизни печальной своей.

Решение:

Обозначим число лет жизни Диофанта за х. Составим и решим уравнение:

+ + + 5 + + 4 = x | ∙84

14x + 7x + 12x + 420 + 42x + 336 = 84x

-9x = -756

x = 84

Оказывается, Диофант умер в 84 года. Но замечательным ученым Диофанта назвали не за умение решать такие уравнения. В его труде «Арифметика» есть уравнения первой степени с одним неизвестным, но главное в этой книге – решение так называемых неопределенных уравнений.

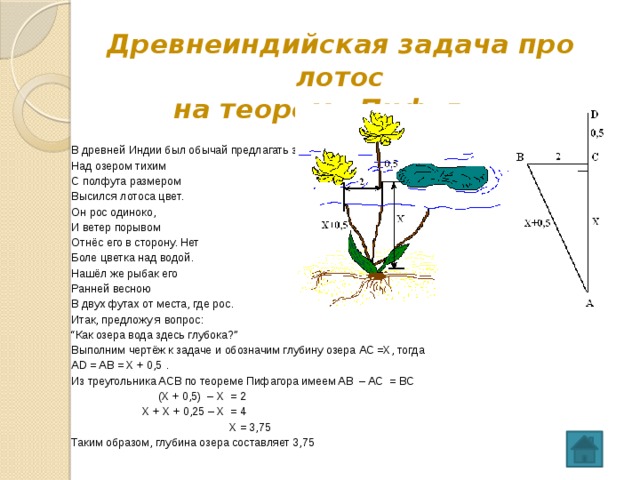
Древнеиндийская задача про лотос на теорему Пифагора

В древней Индии был обычай предлагать задачи в стихах:

Над озером тихим

С полфута размером

Высился лотоса цвет.

Он рос одиноко,

И ветер порывом

Отнёс его в сторону. Нет

Боле цветка над водой.

Нашёл же рыбак его

Ранней весною

В двух футах от места, где рос.

Итак, предложу я вопрос:

“ Как озера вода здесь глубока?”

Выполним чертёж к задаче и обозначим глубину озера АС =Х, тогда

AD = AB = Х + 0,5 .

Из треугольника ACB по теореме Пифагора имеем AB – AC = BC

(Х + 0,5) – Х = 2

Х + Х + 0,25 – Х = 4

Х = 3,75

Таким образом, глубина озера составляет 3,75

Древнеиндийская задача про пчел:

«Есть кадамба-цветок.

На один лепесток

Пчелок пятая часть опустилась.

Рядом тут же росла

Вся в цвету сименгда,

И на ней третья часть поместилась.

Разность их ты найди,

Ее трижды сложи,

На кутай этих пчел посади.

Лишь одна не нашла

Себе места нигде,

Все летала то взад, то вперед и везде

Ароматом цветом наслаждалась.

Назови теперь мне, подсчитавши в уме,

Сколько пчелок всего здесь собралось?»

Решение:1.Алгебраический способ.

Пусть всего собралось х пчелок, тогда имеем уравнение:

+ + 3∙( - ) + 1 = x

3x + 5x + 15x – 9x + 15 = 15x

x = 15

Решив это уравнение, получим ответ:

15 пчел.

2.Способ подбора:

НОК(3; 5) = 15.

Проверим: 15/5 + 15/3 + 3(5 – 3) + 1 =

= 3 + 5 + 6 + 1 = 15

Ответ: было 15 пчел.

Задачи из арабской сказки «1001 ночь»

Задача 1

"Одна женщина отправилась в сад собирать яблоки. Чтобы выйти из сада, ей нужно было пройти через 4 двери, у каждой из которых стоял стражник. Стражнику у первых дверей женщина отдала половину собранных ею яблок. Дойдя до второго стражника, женщина отдала ему половину оставшихся яблок. Так же она поступила и с третьим стражником, а когда она поделилась яблоками со стражником у четвертых дверей, то у нее осталось лишь 10 яблок. Сколько яблок она собрала в саду?"

Решение:

Пусть у женщины было x яблок, тогда первому стражнику она отдала x/2 яблок, второму – x/4 яблок, третьему – x/8 и четвертому – x/16 яблок. Зная, что у неё осталось 10 яблок, составим уравнение

x – ( + + + ) = 10

x – ( ) = 10

x - x = 10

x = 10

x = 160

Значит, женщина собрала 160 яблок.

Задача 2

Стая голубей подлетела к высокому дереву. Часть голубей села на ветвях, а другие расположились под деревом. Сидевшие на ветвях голуби говорят расположившимся внизу: "Если бы один из вас взлетел к нам, то вас стало бы втрое меньше, чем нас всех вместе, а если бы один из нас слетел к вам, то нас с вами стало бы поровну". Сколько голубей сидело на ветвях и сколько под деревом?

Попробуйте решить задачу сами.

Составление математических задач по литературным сюжетам

• Сюжет из повести Н.В.Гоголя «Невский проспект»
• Цитата из «Петербургских новостей»Н.В. Гоголя «Невский проспект»
• Сюжет из повести «Ночь перед рождеством» Н.В. Гоголя 1
• Сюжет из повести «Ночь перед рождеством» Н.В. Гоголя 2

Сюжет из повести Н.В.Гоголя «Невский проспект»

«В один день Пирогов прохаживался по Мещанской, поглядывая на дом под номером 14,на котором красовалась вывеска Шиллера с кофейниками и самоварами; к величайшей радости своей увидел», что сумма номеров домов на одной стороне с этим домом равна 156.

Каким номером дома начинается эта же сторона следующего квартала?

Решение:

Для решения этой задачи необходимо знать формулу суммы n первых членов арифметической прогрессии S = * n, где n – количество домов на четной стороне, a - номер первого дома на этой стороне.

Подставим в формулу данные и найдем n.

* n = 156 (2 + 2n) * n = 312 n 2 + n – 156 = 0

Решая квадратное уравнение, получаем n = 12, т.е. на четной стороне 12 домов и последний дом будет под № 24, а следующий квартал начнется с № 26.

Цитата из «петербургских новостей» Н.В. Гоголя «Невский проспект»

«Нет ничего лучше Невского проспекта, по крайней мере в Петербурге; для него он составляет все» подводит нас еще к одному из образов, послужившего в дальнейшем для составления задачи:

«В 12 часов Невский проспект – педагогический Невский проспект. В это время на него делают набеги гувернеры всех наций со своими питомцами в батистовых воротничках и гувернантки идут величаво позади своих легоньких вертлявых девчонок. Но чем ближе к двум часам там уменьшается их число».

Сколько было гувернанток, гувернеров и детей в 12 часов, если их вместе 160, причем гувернеров меньше в 2 раза, чем гувернанток, и на 20 меньше, чем детей?

Решение:

Пусть гувернеров было х человек, тогда гувернанток – 2х , а гуляющих детей – х +20. Зная, что всего на Невском прогуливалось 160 человек, составим уравнение

х + 2х + х + 20 = 160

4х + 20 = 160

х = 35

Значит, на Невском проспекте прогуливались 35 гувернеров, 70 гувернанток и 55 детей .

Сюжет из повести «Ночь перед рождеством» Н.В. Гоголя

Тут кузнец присел к огромным мешкам, перевязал их покрепче и готовился взвалить их себе на плечи, но один мешок оказался не под силу. Тогда Вакула отсыпал 0,2 мешка и опять не смог поднять, он снова отсыпал 0,5 того, что осталось в мешке. И после этого бодро взвалил себе на плечи. Сколько же мог поднять кузнец, если масса мешка была равна 250 кг?

Решение:

Задачу можно решить, зная правило нахождения части от целого:

1. 250 * (1 – 0,2) = 250 * 0,8 = 200(кг) осталось в мешке после 1-ой отсыпки

2. 200 * (1 – 0,5) = 100(кг) поднял Вакула

Заключение

Вывод:

Авторы, употребляя в своих произведениях числительные и математические данные, не просто так дают готовые знания и выдают все математические секреты, а предлагают нам подумать и дают пищу для размышления.

Данная работа еще раз с большой убедительностью подтверждает знаменитую истину, что математика не признает упрощенного подхода, основанного на фантазии и правдоподобности, и является «царицей всех наук».

Библиографический список

1. Видеман Т.Н. и др. Математика. 10-11 классы: рефераты. – Волгоград: Учитель, 2009. – 287 с.

2. Гоголь Н.В. Вечера на хуторе близ Диканьки. – М.: Худож. лит., 1982. – 431 с.

3. Джек Лондон. Маленькая хозяйка большого дома. – Пермь: Издательство «Капик», 1993. – 367 с.

4. Джонатан Свифт. Путешествие Лемюэля Гулливера. – Москва. Издательство «Правда»,1979.-303 с

5. Жюль Верн. Таинственный остров. – М.: Правда, 1984. – 624 с.

6. Крылов И.А. Басни. – АСТ, Астрель, Хранитель, 2008. – 176 с.

7. Некрасов Н.А. Стихотворения. – М.: Худож. лит., 1985. – 270 с.

8. Перельман Я.И. Веселые задачи. – М.: Астрель: АСТ: Хранитель, 2008. – 287 с.

9. Перельман Я.И. Живая математика. – М., Издательство «Наука», 1974. – 160 с.

10. Пушкин А.С. Полное собрание сочинений в десяти томах. Том 4. – Москва. Издательство «Правда», 1981. - 430 с.

11. Тургенев И.С. Три встречи. – Пермь: Кн.изд-во, 1988. – 277 с.

12. Тысяча и одна ночь: Избр. сказки. – Екатеринбург: Издательство «Ладъ», 1992. – 576 с.

13. Интернет ресурсы: le-savccen.ucoz.ru

wiki.iteach.ru

kaslirina867.narod.ru