| Теория вероятностей
| №1.
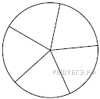
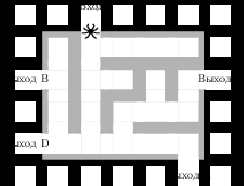
| В магазине три продавца. Каждый из них занят с клиентом с вероятностью 0,7. Найдите вероятность того, что в случайный момент времени все три продавца заняты одновременно (считайте, что клиенты заходят независимо друг от друга). | | №2. | На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук придёт к выходу .
| | №3. | Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с вероятностью 0,5. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,34. Шахматисты А. и Б. играют две партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза. | | №4. | Биатлонист 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,6. Найдите вероятность того, что биатлонист первые 3 раза попал в мишени, а последний раз промахнулся. Результат округлите до сотых.
| | №5. | По отзывам покупателей Пётр Петрович оценил надёжность двух интернет-магазинов. Вероятность того, что нужный товар доставят из магазина А, равна 0,87. Вероятность того, что этот товар доставят из магазина Б, равна 0,92. Пётр Петрович заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар. | | №6. | Вероятность того, что батарейка бракованная, равна 0,02. Покупатель в магазине выбирает случайную упаковку, в которой две таких батарейки. Найдите вероятность того, что обе батарейки окажутся исправными.
| | №7. | Помещение освещается фонарём с тремя лампами. Вероятность перегорания одной лампы в течение года равна 0,19. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
| | №8. | В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,12 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен. |
| №9. | На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Тригонометрия», равна 0,25. Вероятность того, что это вопрос по теме «Внешние углы», равна 0,1. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
| | №10. | Вероятность того, что новый принтер прослужит больше года, равна 0,98. Вероятность того, что он прослужит больше двух лет, равна 0,83. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
| | №11. | Вероятность того, что на тестировании по математике учащийся У. верно решит больше 12 задач, равна 0,78. Вероятность того, что У. верно решит больше 11 задач, равна 0,88. Найдите вероятность того, что У. верно решит ровно 12 задач.
| | №12. | Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 16 пассажиров, равна 0,88. Вероятность того, что окажется меньше 14 пассажиров, равна 0,53. Найдите вероятность того, что число пассажиров будет от 14 до 15. |
|