1-mavzu. Matritsalar va ular ustida amallar
Reja
Matritsaga doir asosiy ta’rif va tushunchalar.
Matritsalar ustida amallar va ularning xossalari.
Tayanch soʻz va iboralar: matritsa, satr matritsa, ustun matritsa, satr-vektor, ustun-vektor, vektor komponenti, nol matritsa, teng matritsa, zanjirlangan matritsalar, kvadrat matritsaning bosh diagonali, diagonal matritsa, skalyar matritsa, birlik matritsa, transponirlangan matritsa, simmetrik matritsa, qiya simmetrik matritsa.
Matritsa tushunchasi va unga asoslangan matematikaning “Matritsalar algebrasi” boʻlimi amaliyotda, jumladan, komрyuter texnologiyalari va dasturlash sohasida muhim ahamiyatga ega.
Matritsa tushunchasi birinchi marta ingliz matematiklari U.Gamilton (1805-1865-y.y.) va A.Kel (1821-1895 y.y.) ishlarida uchraydi. Hozirgi kunda matritsa tushunchasi tabiiy va amaliy jarayonlarning matematik modellarini tuzishda muhim vosita sifatida qoʻllaniladi.
| 1-ta’rif. 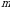 ta satr va ta satr va  ta ustundan iborat boʻlgan qavslar ichiga olingan toʻrtburchakli sonlar jadvaliga matritsa deyiladi. ta ustundan iborat boʻlgan qavslar ichiga olingan toʻrtburchakli sonlar jadvaliga matritsa deyiladi. |
Matritsalar lotin alifbosining bosh harflari bilan belgilanadi. Masalan,
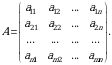
Matritsani tashkil qilgan sonlar uning elementlari deyiladi. Matritsa oʻlchami 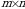 kabi yoziladi. Matritsaning
kabi yoziladi. Matritsaning 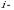 satr,
satr,  ustun kesishmasidagi element
ustun kesishmasidagi element 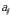 kabi belgilangan. Demak,
kabi belgilangan. Demak, 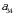 element 3 - satr va 4 - ustun kesishmasida joylashgan elementdir.
element 3 - satr va 4 - ustun kesishmasida joylashgan elementdir.
Ba’zida matritsalarni yozishda (...) qavslar oʻrniga [...] qavslar yoki ||...|| kabi belgilardan foydalaniladi.
Aytaylik quyidagi jadvalda iqtisodiyotning tarmoqlari boʻyicha resurslarning taqsimlanishi berilgan boʻlsin:
| Resurslar | Iqtisodiyot tarmoqlari |
| Sanoat | Qishloq xoʻjaligi |
| Elektr energiyasi resurslari | 7,3 | 5,2 |
| Mehnat resurslari | 4,6 | 3,1 |
| Suv resurslari | 4,8 | 6,1 |
Bu resurslar taqsimotini matritsa koʻrinishida quyidagicha yozish mumkin: 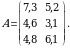 Bu matritsaning oʻlchami
Bu matritsaning oʻlchami 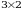 boʻlib, satrlari resurs turlariga ustunlari esa tarmoqlarga mos keladi.
boʻlib, satrlari resurs turlariga ustunlari esa tarmoqlarga mos keladi.
(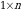 ) oʻlchamli matritsaga satr matritsa, (
) oʻlchamli matritsaga satr matritsa, ( ) oʻlchamli matritsaga esa ustun matritsa deyiladi, ya’ni
) oʻlchamli matritsaga esa ustun matritsa deyiladi, ya’ni
 ,
, 
Bundan tashqari ba’zida bu matritsalar mos ravishda satr-vektor va ustun-vektor deb ham ataladi. Matritsaning elementlari esa vektorlarning komponentlari, deyiladi.
Har bir elementi nolga teng boʻlgan, ixtiyoriy oʻlchamli matritsaga nol matritsa deyiladi va quyidagi koʻrinishda belgilanadi:

1-misol. Quyidagi matritsaviy tenglikdan  va
va 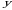 noma’lumlarning qiymatlarini toping:
noma’lumlarning qiymatlarini toping:
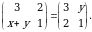
Yechish. Matritsalarning mos elementlarini tenglab quyidagi tengliklarni hosil qilamiz:
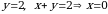 .
.
Masalan,  va
va 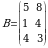 matritsalar zanjirlangan matritsalar boʻladi. Chunki,
matritsalar zanjirlangan matritsalar boʻladi. Chunki, 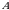 matritsaning oʻlchami
matritsaning oʻlchami 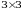 ga,
ga,  matritsaning oʻlchami
matritsaning oʻlchami 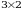 ga teng.
ga teng.
Shuni ta’kidlash lozimki  va
va 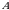 matritsalar zanjirlangan emas. Chunki,
matritsalar zanjirlangan emas. Chunki,  matritsaning ustunlari soni 2 ga,
matritsaning ustunlari soni 2 ga, 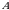 matritsaning satrlari soni 3 ga teng boʻlib, oʻzaro bir xil emas.
matritsaning satrlari soni 3 ga teng boʻlib, oʻzaro bir xil emas.
| 4-ta’rif. Satrlari va ustunlari soni oʻzaro teng boʻlgan matritsaga kvadrat matritsa deyiladi. |
Masalan,  matritsa 4-tartibli kvadrat matritsadir.
matritsa 4-tartibli kvadrat matritsadir. 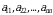 elementlarning tartiblangan tо‘plami kvadrat matritsaning asosiy diagonali deyiladi.
elementlarning tartiblangan tо‘plami kvadrat matritsaning asosiy diagonali deyiladi.

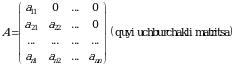
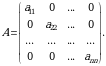
| 7-ta’rif. Agar diagonal matritsaning barcha diagonal elementlari oʻzaro teng boʻlsa, u holda bunday matritsaga skalyar matritsa deyiladi ya’ni
|

| 8-ta’rif. Agar skalyar matritsada 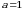 boʻlsa, u holda bunday matritsaga birlik matritsa deyiladi va odatda boʻlsa, u holda bunday matritsaga birlik matritsa deyiladi va odatda 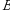 harfi bilan belgilanadi, ya’ni harfi bilan belgilanadi, ya’ni
|
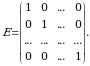
Oʻlchamlari aynan teng boʻlgan matritsalar ustidagina algebraik qoʻshish amali bajariladi.
Oʻlchamlari aynan teng boʻlgan
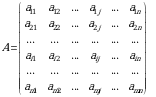 va
va 
matritsalarni qoʻshish uchun, ularning mos elementlari qoʻshiladi, y’ani

Matritsani biror haqiqiy 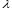 songa koʻpaytirish uchun bu son matritsaning har bir elementiga koʻpaytiriladi, y’ani
songa koʻpaytirish uchun bu son matritsaning har bir elementiga koʻpaytiriladi, y’ani

Ikkita matritsa ayirmasi quyidagicha topiladi:

2-misol. Quyidagi matritsalarning yigʻindisi va ayirmasini toping:
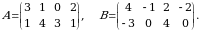
Yechish.  va
va 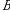 matritsalarning oʻlchamlari
matritsalarning oʻlchamlari 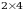 ga teng. Shu sababli bu matritsalarni qoʻshish va ayirish mumkin. Ta’rifga asosan
ga teng. Shu sababli bu matritsalarni qoʻshish va ayirish mumkin. Ta’rifga asosan

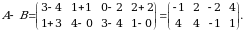
3-misol. Quyidagi  matritsani
matritsani 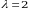 soniga koʻpaytiring:
soniga koʻpaytiring:
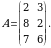
Yechish. 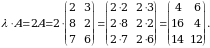
4-misol. Firma 5 turdagi mahsulotni ikkita korxonada ishlab chiqaradi. Firmaning ishlab chiqargan mahsulotlari taqsimoti quyidagi jadvalda berilgan:
| Mahsulot turlari | 1 | 2 | 3 | 4 | 5 |
| 1-korxonada ishlab chiqarilgan mahsulotlar miqdori | 139 | 160 | 205 | 340 | 430 |
| 2-korxonada ishlab chiqarilgan mahsulotlar miqdori | 122 | 130 | 145 | 162 | 152 |
Firma ishlab chiqarish uskunalarini yangilash natijasida ishlab chiqarishni 17% ga oshirdi. Firma ishlab chiqarish uskunalarini yangilagandan keyin, firmaning bir oyda ishlab chiqargan mahsulotlari taqsimoti qanday boʻladi?
Yechish. Firmaning ishlab chiqarish uskunalarini yangilamasdan oldingi ishlab chiqargan mahsulotlari taqsimotini quyidagi matritsa koʻrinishda yozish mumkin:
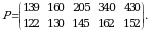
Firma ishlab chiqarish uskunalarini yangilagandan keyin, firmaning bir oyda ishlab chiqargan mahsulotlari taqsimotini topish uchun, bu ishlab chiqarish matritsasini 1,17 ga koʻpaytirish zarur boʻladi:
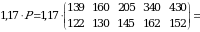

Matritsalarni qoʻshish, ayirish va matritsani songa koʻpaytirish amallariga matritsalar ustida chiziqli amallar deyiladi.
Matritsalarni qoʻshish va songa koʻpaytirish amallari quyidagi xossalarga boʻysinadi:
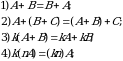
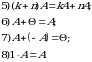
Bu yеrda 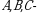 bir xil o‘lchamli matritsalar,
bir xil o‘lchamli matritsalar,  matritsa esa
matritsa esa 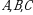 matritsalar bilan bir xil o‘lchamli nol matritsa,
matritsalar bilan bir xil o‘lchamli nol matritsa, 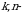 ixtiyoriy haqiqiy sonlar.
ixtiyoriy haqiqiy sonlar.
Matritsalarni koʻpaytirish amali faqatgina zanjirlangan matritsalar ustida bajariladi.
Bu formuladan koʻrish mumkinki,  va
va 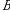 matritsalarning koʻpaytmasi
matritsalarning koʻpaytmasi  matritsadagi
matritsadagi 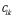 element
element  matritsaning
matritsaning 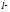 satrida joylashgan har bir elementni
satrida joylashgan har bir elementni 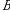 matritsaning
matritsaning  ustunida joylashgan mos oʻrindagi elementga koʻpaytirish va hosil boʻlgan koʻpaytmalarni qoʻshish natijasida aniqlanadi.
ustunida joylashgan mos oʻrindagi elementga koʻpaytirish va hosil boʻlgan koʻpaytmalarni qoʻshish natijasida aniqlanadi.
Masalan, bizga umumiy holda  va
va 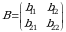 koʻrinishdagi matritsalar berilgan boʻlsin. Bu matritsalarni koʻpaytirish quyidagicha amalga oshiriladi:
koʻrinishdagi matritsalar berilgan boʻlsin. Bu matritsalarni koʻpaytirish quyidagicha amalga oshiriladi:
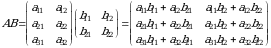 .
.
Endi buni aniq misollarda koʻrib chiqamiz.
5-misol. Quyidagi  matritsani
matritsani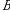 matritsaga koʻpaytiring:
matritsaga koʻpaytiring:

Yechish. 1. Izlanayotgan 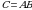 matritsaning
matritsaning 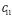 elementi
elementi  matritsaning birinchi satr elementlarini
matritsaning birinchi satr elementlarini 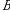 matritsaning birinchi ustun mos elementlari bilan koʻpaytmalarining yigʻindisiga teng, ya’ni
matritsaning birinchi ustun mos elementlari bilan koʻpaytmalarining yigʻindisiga teng, ya’ni
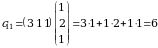 .
.
2. Izlanayotgan 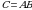 matritsaning birinchi satr va ikkinchi ustunining elementi
matritsaning birinchi satr va ikkinchi ustunining elementi  matritsaning birinchi satr elementlarini
matritsaning birinchi satr elementlarini 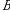 matritsaning ikkinchi ustun elementlari bilan mos ravishda koʻpaytmalarining yigʻindisiga teng:
matritsaning ikkinchi ustun elementlari bilan mos ravishda koʻpaytmalarining yigʻindisiga teng:
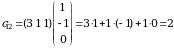 .
.
3. Birinchi satr va uchinchi ustun elementi
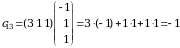
kabi aniqlanadi.
4. Izlanayotgan matritsaning ikkinchi satr elementlari  matritsaning ikkinchi satr elementlarining
matritsaning ikkinchi satr elementlarining 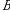 matritsaning mos ravishda 1, 2, 3-ustun elementlari bilan koʻpaytmalarining yigʻindisi sifatida topiladi:
matritsaning mos ravishda 1, 2, 3-ustun elementlari bilan koʻpaytmalarining yigʻindisi sifatida topiladi:

5.  matritsaning uchinchi satr elementlari ham shunga oʻxshash topiladi:
matritsaning uchinchi satr elementlari ham shunga oʻxshash topiladi:
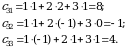
Shunday qilib,
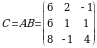 .
.
6-misol. Quyidagi  va
va 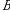 matritsalar uchun
matritsalar uchun 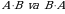 koʻpaytmalarni toping:
koʻpaytmalarni toping:


Yechish. Bu matritsalar zanjirlangan boʻlganligi sababli ular ustida koʻpaytirish amali bajariladi.

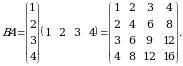
Keltirilgan misoldan koʻrinib turibdiki,  va
va  matritsalarning koʻpaytmasi kommutativlik (oʻrin almashtirish) xossasiga ega emas, ya’ni
matritsalarning koʻpaytmasi kommutativlik (oʻrin almashtirish) xossasiga ega emas, ya’ni 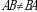 . Agar
. Agar  va
va 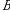 bir xil tartibli kvadrat matritsalar boʻlsa,
bir xil tartibli kvadrat matritsalar boʻlsa, 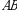 va
va 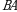 koʻpaytmalarini topish mumkin. Agar
koʻpaytmalarini topish mumkin. Agar 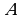 va
va 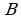 matritsalar uchun
matritsalar uchun 
 munosabat o‘rinli bo‘lsa, u holda
munosabat o‘rinli bo‘lsa, u holda 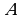 va
va 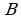 matritsalar kommutativ (antikommutativ) matritsalar deyiladi. Masalan,
matritsalar kommutativ (antikommutativ) matritsalar deyiladi. Masalan, 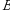 birlik matritsa ixtiyoriy
birlik matritsa ixtiyoriy  kvadrat matritsa bilan kommutativdir. Haqiqatan ham
kvadrat matritsa bilan kommutativdir. Haqiqatan ham
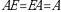 .
.
Matritsalarni koʻpaytirish amali quyidagi xossalarga ega:

Keltirilgan xossalardan toʻrtinchisini quyidagi misol yordamida tekshiramiz.
7-misol. 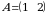 ,
,  va
va 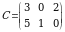 matritsalar berilgan boʻlsin:
matritsalar berilgan boʻlsin:
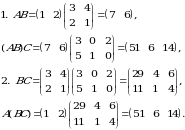
Koʻrinib turibdiki, ikki xil hisoblash usulida ham natija bir xil.
Transponirlangan matritsalar quyidagi xossalarga ega:
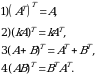
Masalan, 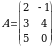 boʻlsa,
boʻlsa,  boʻladi.
boʻladi.
| 12-ta’rif. Agar kvadrat matritsa uchun kvadrat matritsa uchun 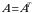 munosabat oʻrinli boʻlsa, u holda bu matritsaga simmetrik matritsa deyiladi. munosabat oʻrinli boʻlsa, u holda bu matritsaga simmetrik matritsa deyiladi. |
Masalan,  simmetrik matritsaning elementlari bosh diagonalga nisbatan simmetrik joylashgan.
simmetrik matritsaning elementlari bosh diagonalga nisbatan simmetrik joylashgan.
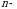 tartibli simmetrik matritsaning turli elementlari soni koʻpi bilan
tartibli simmetrik matritsaning turli elementlari soni koʻpi bilan  ga teng, bunda
ga teng, bunda 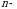 natural son.
natural son.
| 13-ta’rif. Agar 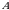 kvadrat matritsada kvadrat matritsada 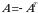 munosabat oʻrinli boʻlsa, bunday matritsaga qiya simmetrik matritsa deb ataladi. munosabat oʻrinli boʻlsa, bunday matritsaga qiya simmetrik matritsa deb ataladi. |
Masalan,

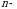 tartibli qiya simmetrik matritsaning turli elementlari soni koʻpi bilan
tartibli qiya simmetrik matritsaning turli elementlari soni koʻpi bilan  formula yordamida topiladi, bunda
formula yordamida topiladi, bunda 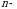 natural son.
natural son.
14-ta’rif. Nolmas satrlarga ega  matritsada har qanday
matritsada har qanday 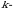 nolmas satrning birinchi noldan farqli elementi
nolmas satrning birinchi noldan farqli elementi 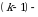 nolmas satrning birinchi noldan farqli elementidan oʻngda tursa, u holda
nolmas satrning birinchi noldan farqli elementidan oʻngda tursa, u holda  pog‘onasimon matritsa deyiladi.
pog‘onasimon matritsa deyiladi.
Masalan, 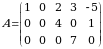 matritsa pog‘onasimon matritsadir.
matritsa pog‘onasimon matritsadir.
7-misol. Korxona ikki turdagi transformatorlar ishlab chiqaradi. 1-turdagi transformator ishlab chiqarish uchun 5 kg temir va 3 kg sim, 2-turdagi transformator ishlab chiqarish uchun 3 kg temir va 2 kg sim sarflanadi. Bir birlik transformatorlarni sotishdan mos ravishda 6 va 5 sh.p.b. miqdorida daromad olinadi. Korxonaning omborida 4,5 tonna temir va 3 tonna sim mavjud. Texnologik matritsa, narxlar vektori va resurs zahirasini ifodalovchi vektorni tuzing.  rejalar joiz reja boʻla oladimi?
rejalar joiz reja boʻla oladimi?
Yechish. Korxona ikki turdagi resursdan foydalanib 2 turdagi mahsulot ishlab chiqaradi. Narxlar vektori  . Resurs zahiralari vektori
. Resurs zahiralari vektori 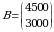 . Texnologik (resurs sarfi normasi) matritsa
. Texnologik (resurs sarfi normasi) matritsa 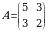 .
.
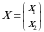 rejani qaraymiz. Bu rejani bajarishdagi resurs sarfi
rejani qaraymiz. Bu rejani bajarishdagi resurs sarfi
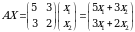
ga teng. Bu sarf zahiradan oshib ketmasligi kerak, ya’ni  yoki
yoki
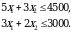
Joiz reja yuqoridagi tengsizliklarni qanoatlantirishi zarur.
1) 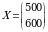 rejani qaraymiz. U holda
rejani qaraymiz. U holda
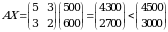 ,
,
ya’ni bu reja joiz reja. Bu reja asosida olinadigan daromad miqdori 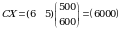 sh.p.b. ga teng.
sh.p.b. ga teng.
2)  rejani qaraymiz. U holda
rejani qaraymiz. U holda
 .
.
Bundan koʻrish mimkinki, 1-turdagi resurs sarfi 4800 ga teng boʻlib, resurs zahirasi 4500 dan katta. Shu sababli, qaralayotgan reja joiz reja emas.
8-misol. Korxona 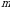 turdagi resurslarni qo‘llab,
turdagi resurslarni qo‘llab,  turdagi mahsulot ishlab chiqaradi.
turdagi mahsulot ishlab chiqaradi. 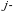 turdagi mahsulot birligini ishlab chiqarishga ketgan
turdagi mahsulot birligini ishlab chiqarishga ketgan 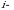 xom ashyo resurslari harajatlarining normalari
xom ashyo resurslari harajatlarining normalari 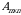 matritsa bilan berilgan. Vaqtning ma’lum oralig‘ida korxona har bir turdagi mahsulotdan
matritsa bilan berilgan. Vaqtning ma’lum oralig‘ida korxona har bir turdagi mahsulotdan  miqdorini ishlab chiqargan bo‘lsin. Uni
miqdorini ishlab chiqargan bo‘lsin. Uni matritsa bilan ifodalaymiz.
matritsa bilan ifodalaymiz.
Vaqtning berilgan davrida barcha mahsulotning har bir turini ishlab chiqarishga ketgan resurslarning to‘la harajatlar matritsasi  ni aniqlang. Berilgan
ni aniqlang. Berilgan
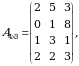
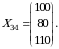
Yechish. Resurslarning to‘la harajatlar matritsasi 
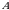 va
va  matritsalarning kо‘paytmasi sifatida aniqlanadi, ya’ni
matritsalarning kо‘paytmasi sifatida aniqlanadi, ya’ni 
Berilgan masalaning sharti bо‘yicha
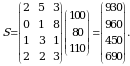
Berilgan vaqt orlig‘ida 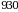 birlik I turdagi resurs,
birlik I turdagi resurs, 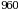 birlik II turdagi resurs,
birlik II turdagi resurs, 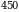 birlik III turdagi resurs,
birlik III turdagi resurs, 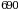 birlik IV turdagi resurs sarf qilingan.
birlik IV turdagi resurs sarf qilingan.
9-misol. Korxona mahsulotning  turini ishlab chiqaradi, ishlab chiqariladigan mahsulot hajmlari
turini ishlab chiqaradi, ishlab chiqariladigan mahsulot hajmlari 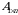 matritsa bilan berilgan.
matritsa bilan berilgan. 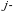 mintaqada mahsulotning
mintaqada mahsulotning 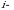 turi birligining sotilish narxi
turi birligining sotilish narxi  matritsa bilan berilgan, bu yerda
matritsa bilan berilgan, bu yerda 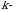 mahsulot sotilayotgan mintaqalar soni.
mahsulot sotilayotgan mintaqalar soni.
Mintaqalar bo‘yicha daromad matritsasi 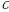 ni toping.
ni toping.
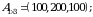
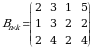 bo‘lsin.
bo‘lsin.
Yechish. Daromad 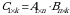 matritsa bilan aniqlanadi,
matritsa bilan aniqlanadi, 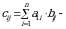 bu
bu 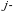 mintaqada korxonaning daromadi quyidagicha:
mintaqada korxonaning daromadi quyidagicha:

O‘z-o‘zini tekshirish uchun savollar
Matritsa deb nimaga aytiladi?
Satr matritsa, ustun matritsa deb qanday matritsaga aytiladi?
Nol matritsa deb qanday matritsaga aytiladi?
Matritsalarni qo’shish va matritsani songa ko’paytirish amallari bo’ysunadigan xossalarni sanab o’ting?
Matritsa satrlarini mos ustunlari bilan almashtirish amali qanday nomlanadi?
O’zaro zanjirlangan matritsalar qanday ko’paytiriladi?
Matritsalarni ko’paytirish amali qanday xossalarga bo’ysunadi?
Matritsalarni ko’paytirish amali o’rin almashtirish qonuniga bo’ysunadimi?
n-tartibli kvadratik matritsa deb qanday matritsaga aytiladi?
Kvadrat matritsaning qanday xususiy ko’rinishlarini bilasiz?
Asosiy adabiyotlar:
Gilbert Strang “Introduction to Linear Algebra”, USA, Cambridge press, 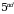 Edition, 2016.
Edition, 2016.
Grewal B.S. “Higher Engineering Mathematics”, Delhi, Khanna publishers, 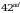 Edition, 2012.
Edition, 2012.
Raxmatov R.R., Adizov A.A., Tadjibayeva Sh.E., Shoimardonov S.K. Chiziqli algebra va analitik geometriya. O‘quv qollanma. Toshkent 2020.
Rаxмаtоv R.R., Adizov A.A. “Chiziqli fazo va chiziqli operatorlar” O‘quv uslubiy qollanma. TATU, Toshkent 2019.
Соатов Ё.У. “Олий математика”, Т., Ўқитувчи нашриёти, 1- 5 қисмлар, 1995.
Рябушко А.П. и др. “Сборник индивидуальных заданий по высшей математике”, Минск, Высшая школа, 1-3 частях, 1991.
Asosiy adabiyotlar:
Мирзиёев Ш. Буюк келажагимизни мард ва олижаноб халқимиз билан бирга қурамиз. –Т.: Ўзбекистон, 2017. - 488 бет.
Мирзиёев Ш.М. Қонун устуворлиги ва инсон манфаатларини таъминлаш-юрт тараққиёти ва халқ фаровонлигининг гарови. –Т.: Ўзбекистон, 2017.
Мирзиёев Ш.М. Эркин ва фаровон, демократик Ўзбекистон давлатини биргаликда барпо этамиз. Т.: Ўзбекистон, 2017.
Adizov A.A., Xudoyberganov M.O‘. Amaliy matematika. O‘quv uslubiy qo‘llanma. Toshkent. 2014.
Шодиев Т.Ш. Аналитик геометрия ва чизиқли алгебра. Тошкент “Ўқитувчи” 1984.
Ильин В. А., Позняк Э. Г. Линейная алгебра. — 6-е изд., стер. — М.: ФИЗМАТЛИТ, 2004.
Задорожный В. Н. и др. Высшая математика для технических
университетов. Часть I. Линейная алгебра. - Томск: Изд-во ТПУ, 2009.
Данко П.С., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Седьмое издание. -М.: Высшая; школа, 2015.
Семёнова Т.В. Высшая математика: учебное пособие для студентов технических вузов. Часть 1. - Пенза: Пензенский гос. ун-т, 2008.
Макаров Е. В., Лунгу К. Н. Высшая математика: руководство к решению задач: учебное пособие, Часть 1, Физматлит. 2013.
Минорский В.И. Сборник задач по высшей математике. М: Наука, 1987.
Беклемешев Д.В., Петрович А.Ю., Чуберов И.А. Сборник задач по аналитической геометрии и линейной алгебре. -М.: Наука, 1987.
Бугров Я.С., Николский С.М. Сборник задач по высшей математике, - М.: Наука. 1997.







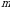 ta satr va
ta satr va  ta ustundan iborat boʻlgan qavslar ichiga olingan toʻrtburchakli sonlar jadvaliga matritsa deyiladi.
ta ustundan iborat boʻlgan qavslar ichiga olingan toʻrtburchakli sonlar jadvaliga matritsa deyiladi.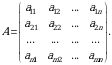
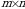 kabi yoziladi. Matritsaning
kabi yoziladi. Matritsaning 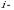 satr,
satr,  ustun kesishmasidagi element
ustun kesishmasidagi element 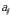 kabi belgilangan. Demak,
kabi belgilangan. Demak, 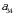 element 3 - satr va 4 - ustun kesishmasida joylashgan elementdir.
element 3 - satr va 4 - ustun kesishmasida joylashgan elementdir.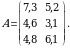 Bu matritsaning oʻlchami
Bu matritsaning oʻlchami 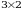 boʻlib, satrlari resurs turlariga ustunlari esa tarmoqlarga mos keladi.
boʻlib, satrlari resurs turlariga ustunlari esa tarmoqlarga mos keladi.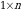 ) oʻlchamli matritsaga satr matritsa, (
) oʻlchamli matritsaga satr matritsa, ( ) oʻlchamli matritsaga esa ustun matritsa deyiladi, ya’ni
) oʻlchamli matritsaga esa ustun matritsa deyiladi, ya’ni ,
, 

 va
va  matritsalarning oʻlchamlari bir xil boʻlib, ularning barcha mos elementlari oʻzaro teng boʻlsa, bunday matritsalar teng matritsalar deyiladi va
matritsalarning oʻlchamlari bir xil boʻlib, ularning barcha mos elementlari oʻzaro teng boʻlsa, bunday matritsalar teng matritsalar deyiladi va 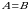 koʻrinishda yoziladi.
koʻrinishda yoziladi. va
va 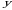 noma’lumlarning qiymatlarini toping:
noma’lumlarning qiymatlarini toping: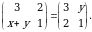
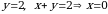 .
.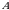 matritsaning ustunlari soni
matritsaning ustunlari soni  matritsaning satrlari soniga teng boʻlsa, u holda
matritsaning satrlari soniga teng boʻlsa, u holda 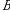 matritsa bilan zanjirlangan matritsa deyiladi.
matritsa bilan zanjirlangan matritsa deyiladi. va
va 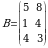 matritsalar zanjirlangan matritsalar boʻladi. Chunki,
matritsalar zanjirlangan matritsalar boʻladi. Chunki, 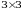 ga,
ga,  matritsa 4-tartibli kvadrat matritsadir.
matritsa 4-tartibli kvadrat matritsadir. 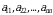 elementlarning tartiblangan tо‘plami kvadrat matritsaning asosiy diagonali deyiladi.
elementlarning tartiblangan tо‘plami kvadrat matritsaning asosiy diagonali deyiladi.  kvadrat matritsada barcha
kvadrat matritsada barcha 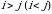 lar uchun
lar uchun 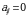 boʻlsa, u holda
boʻlsa, u holda  matritsa yuqori (quyi) uchburchakli matritsa deyiladi.
matritsa yuqori (quyi) uchburchakli matritsa deyiladi.
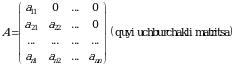
 ) va qolgan barcha elementlari nolga teng (ya’ni,
) va qolgan barcha elementlari nolga teng (ya’ni,  ) boʻlsa, u holda
) boʻlsa, u holda 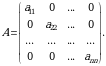

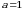 boʻlsa, u holda bunday matritsaga birlik matritsa deyiladi va odatda
boʻlsa, u holda bunday matritsaga birlik matritsa deyiladi va odatda 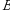 harfi bilan belgilanadi, ya’ni
harfi bilan belgilanadi, ya’ni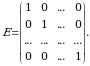
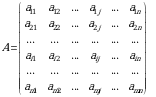 va
va 

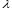 songa koʻpaytirish uchun bu son matritsaning har bir elementiga koʻpaytiriladi, y’ani
songa koʻpaytirish uchun bu son matritsaning har bir elementiga koʻpaytiriladi, y’ani

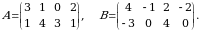
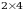 ga teng. Shu sababli bu matritsalarni qoʻshish va ayirish mumkin. Ta’rifga asosan
ga teng. Shu sababli bu matritsalarni qoʻshish va ayirish mumkin. Ta’rifga asosan
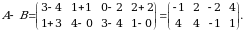
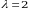 soniga koʻpaytiring:
soniga koʻpaytiring: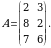
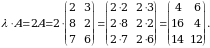
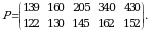
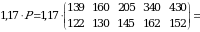

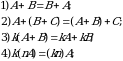
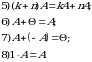
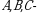 bir xil o‘lchamli matritsalar,
bir xil o‘lchamli matritsalar,  matritsa esa
matritsa esa 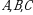 matritsalar bilan bir xil o‘lchamli nol matritsa,
matritsalar bilan bir xil o‘lchamli nol matritsa, 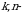 ixtiyoriy haqiqiy sonlar.
ixtiyoriy haqiqiy sonlar. oʻlchamli
oʻlchamli  oʻlchamli
oʻlchamli 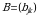 matritsaga koʻpaytmasi deb elementlari
matritsaga koʻpaytmasi deb elementlari 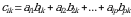 qoida bilan aniqlanadigan
qoida bilan aniqlanadigan  matritsaga aytiladi.
matritsaga aytiladi. matritsadagi
matritsadagi 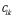 element
element 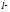 satrida joylashgan har bir elementni
satrida joylashgan har bir elementni  ustunida joylashgan mos oʻrindagi elementga koʻpaytirish va hosil boʻlgan koʻpaytmalarni qoʻshish natijasida aniqlanadi.
ustunida joylashgan mos oʻrindagi elementga koʻpaytirish va hosil boʻlgan koʻpaytmalarni qoʻshish natijasida aniqlanadi. va
va 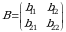 koʻrinishdagi matritsalar berilgan boʻlsin. Bu matritsalarni koʻpaytirish quyidagicha amalga oshiriladi:
koʻrinishdagi matritsalar berilgan boʻlsin. Bu matritsalarni koʻpaytirish quyidagicha amalga oshiriladi: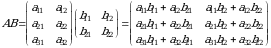 .
.
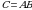 matritsaning
matritsaning 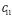 elementi
elementi 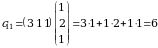 .
.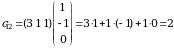 .
.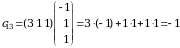

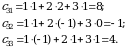
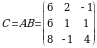 .
.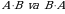 koʻpaytmalarni toping:
koʻpaytmalarni toping:


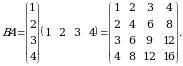
 va
va  matritsalarning koʻpaytmasi kommutativlik (oʻrin almashtirish) xossasiga ega emas, ya’ni
matritsalarning koʻpaytmasi kommutativlik (oʻrin almashtirish) xossasiga ega emas, ya’ni 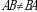 . Agar
. Agar 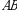 va
va 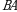 koʻpaytmalarini topish mumkin. Agar
koʻpaytmalarini topish mumkin. Agar 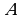 va
va 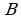 matritsalar uchun
matritsalar uchun 
 munosabat o‘rinli bo‘lsa, u holda
munosabat o‘rinli bo‘lsa, u holda 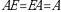 .
.
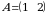 ,
,  va
va 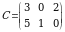 matritsalar berilgan boʻlsin:
matritsalar berilgan boʻlsin: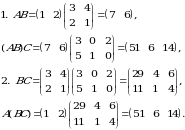
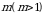 butun musbat darajaga ko‘tarish quyidagicha amalga oshiriladi:
butun musbat darajaga ko‘tarish quyidagicha amalga oshiriladi: 
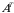 matritsa
matritsa 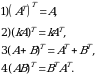
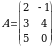 boʻlsa,
boʻlsa,  boʻladi.
boʻladi.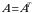 munosabat oʻrinli boʻlsa, u holda bu matritsaga simmetrik matritsa deyiladi.
munosabat oʻrinli boʻlsa, u holda bu matritsaga simmetrik matritsa deyiladi. simmetrik matritsaning elementlari bosh diagonalga nisbatan simmetrik joylashgan.
simmetrik matritsaning elementlari bosh diagonalga nisbatan simmetrik joylashgan.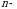 tartibli simmetrik matritsaning turli elementlari soni koʻpi bilan
tartibli simmetrik matritsaning turli elementlari soni koʻpi bilan  ga teng, bunda
ga teng, bunda 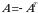 munosabat oʻrinli boʻlsa, bunday matritsaga qiya simmetrik matritsa deb ataladi.
munosabat oʻrinli boʻlsa, bunday matritsaga qiya simmetrik matritsa deb ataladi.
 formula yordamida topiladi, bunda
formula yordamida topiladi, bunda 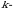 nolmas satrning birinchi noldan farqli elementi
nolmas satrning birinchi noldan farqli elementi 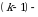 nolmas satrning birinchi noldan farqli elementidan oʻngda tursa, u holda
nolmas satrning birinchi noldan farqli elementidan oʻngda tursa, u holda 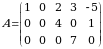 matritsa pog‘onasimon matritsadir.
matritsa pog‘onasimon matritsadir. rejalar joiz reja boʻla oladimi?
rejalar joiz reja boʻla oladimi?  . Resurs zahiralari vektori
. Resurs zahiralari vektori 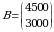 . Texnologik (resurs sarfi normasi) matritsa
. Texnologik (resurs sarfi normasi) matritsa 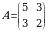 .
.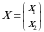 rejani qaraymiz. Bu rejani bajarishdagi resurs sarfi
rejani qaraymiz. Bu rejani bajarishdagi resurs sarfi 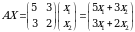
 yoki
yoki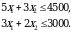
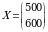 rejani qaraymiz. U holda
rejani qaraymiz. U holda 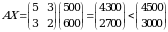 ,
,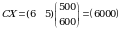 sh.p.b. ga teng.
sh.p.b. ga teng.  rejani qaraymiz. U holda
rejani qaraymiz. U holda  .
.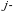 turdagi mahsulot birligini ishlab chiqarishga ketgan
turdagi mahsulot birligini ishlab chiqarishga ketgan 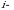 xom ashyo resurslari harajatlarining normalari
xom ashyo resurslari harajatlarining normalari 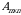 matritsa bilan berilgan. Vaqtning ma’lum oralig‘ida korxona har bir turdagi mahsulotdan
matritsa bilan berilgan. Vaqtning ma’lum oralig‘ida korxona har bir turdagi mahsulotdan  miqdorini ishlab chiqargan bo‘lsin. Uni
miqdorini ishlab chiqargan bo‘lsin. Uni matritsa bilan ifodalaymiz.
matritsa bilan ifodalaymiz.  ni aniqlang. Berilgan
ni aniqlang. Berilgan 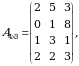
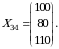
 matritsalarning kо‘paytmasi sifatida aniqlanadi, ya’ni
matritsalarning kо‘paytmasi sifatida aniqlanadi, ya’ni 
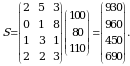
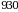 birlik I turdagi resurs,
birlik I turdagi resurs, 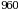 birlik II turdagi resurs,
birlik II turdagi resurs, 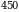 birlik III turdagi resurs,
birlik III turdagi resurs, 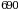 birlik IV turdagi resurs sarf qilingan.
birlik IV turdagi resurs sarf qilingan. 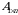 matritsa bilan berilgan.
matritsa bilan berilgan.  matritsa bilan berilgan, bu yerda
matritsa bilan berilgan, bu yerda 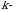 mahsulot sotilayotgan mintaqalar soni.
mahsulot sotilayotgan mintaqalar soni.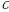 ni toping.
ni toping.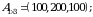
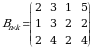 bo‘lsin.
bo‘lsin.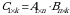 matritsa bilan aniqlanadi,
matritsa bilan aniqlanadi, 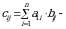 bu
bu 
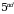 Edition, 2016.
Edition, 2016. 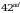 Edition, 2012.
Edition, 2012. 









