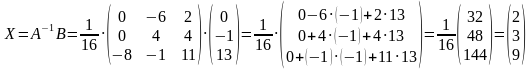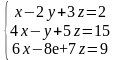Занятие 9. Тема «Метод Гаусса и матричный метод решения систем линейных уравнений»
План лекции:
-
Метод Гаусса
-
Матричный метод
-
Самостоятельная работа для студентов
Метод Гаусса
Метод Гаусса прекрасно подходит для решения систем линейных алгебраических уравнений (СЛАУ). Он обладает рядом преимуществ по сравнению с другими методами:
-
Во-первых, нет необходимости предварительно исследовать систему уравнений на совместность;
-
Во-вторых, методом Гаусса позволяет решить совместные и неопределенные системы, когда ранги основной матрицы и расширенной матрицы меньше числа переменных в системе.
Метод Гаусса решения систем линейных уравнений состоит из двух этапов, называемых прямым и обратным ходом.
Прямой ход метода Гаусса заключается в том, что с помощью элементарных преобразований над расширенной матрицей система приводится к «ступенчатому» виду.
Обратный ход метода Гаусса состоит в том, что, из полученной ступенчатой матрицы нужно перейти к новой системе (ступенчатой), из которой, начиная с последнего уравнения, вычисляются неизвестные.
Пример 1. Решить систему линейных уравнений методом Гаусса.
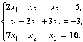
Прямой ход. Приведём расширенную матрицу системы к ступенчатому виду
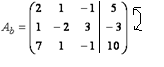

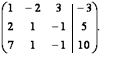

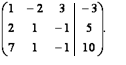

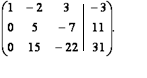

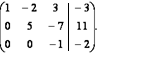
Обратный ход. Первый столбец умножается на первую переменную, второй столбец умножается на вторую переменную, третий столбец – на третью переменную в каждой строке. И каждую строку приравниваем на элемент из четвертого столбца. Таким образом, мы привели полученную ступенчатую расширенную матрицу к новой системе уравнений, которая также является ступенчатой: 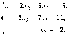
Начиная с последнего уравнения полученной ступенчатой системы уравнений, последовательно найдём значения неизвестных: х3=2, подставляем х3 во второе уравнение и находим х2=5. Затем найденные х2 и х3 подставляем в первое уравнение и находим х1=1.
Итак, ответ записываем следующим образом (1; 5;2)
Матричный метод
Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными:
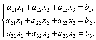
Рассмотрим матрицу системы 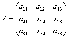 и матрицы столбцы неизвестных и свободных членов
и матрицы столбцы неизвестных и свободных членов 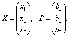 . Тогда систему можно записать в матричном виде:
. Тогда систему можно записать в матричном виде:
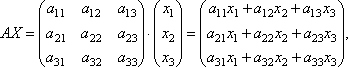
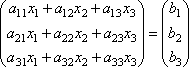 или короче A∙X=B.
или короче A∙X=B.
Пусть определитель матрицы отличен от нуля |A| ≠ 0. Тогда матричное уравнение решается следующим образом Х=А-1В.
Заметим, что поскольку обратную матрицу можно найти только для квадратных матриц, то матричным методом можно решать только те системы, в которых число уравнений совпадает с числом неизвестных.
Итак, чтобы решить систему линейных уравнений матричным методом, нужно найти для основной матрицы системы обратную ей матрицу и умножить её на столбец свободных членов.
Пример. Решить систему линейных уравнений матричным методом:
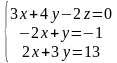
Вычислим определитель матрицы А:
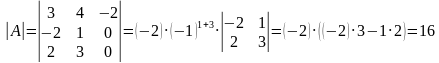
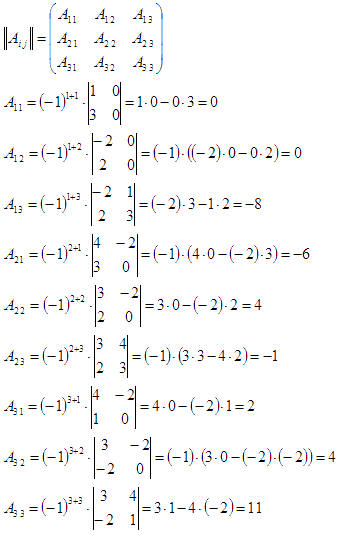
Теперь находим обратную матрицу как  :
:

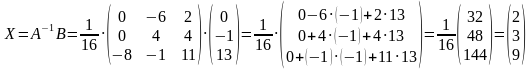
Самостоятельная работа для студентов
-
Переписать лекцию и прислать фото СЕГОДНЯ
-
Пользуясь этим теоретическим материалом решить систему линейных уравнений двумя методами – методом Гаусса и матричным методом.
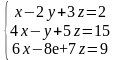
-
Фото лекции прислать до субботы. Методом Гаусса прислать в виде фото личным сообщением выполненное задание до воскресенья, а матричный метод до понедельника.







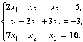
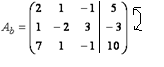

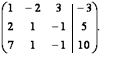
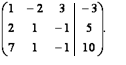
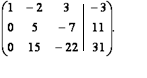
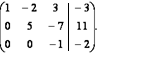
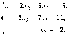
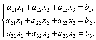
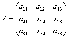 и матрицы столбцы неизвестных и свободных членов
и матрицы столбцы неизвестных и свободных членов 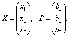 . Тогда систему можно записать в матричном виде:
. Тогда систему можно записать в матричном виде: 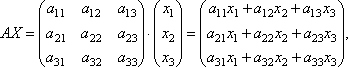
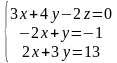
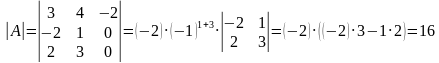
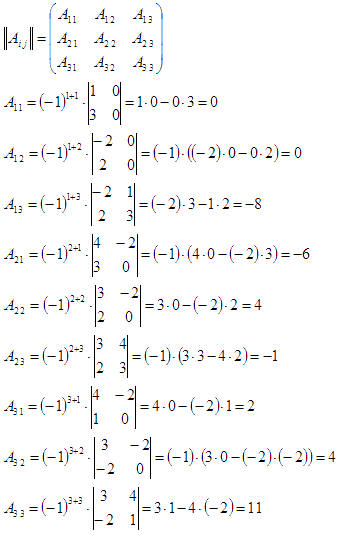
 :
: