Дата 01.04.2020
Тема урока: МЕТОД ИНТЕРВАЛОВ ДЛЯ НЕПРЕРЫВНЫХ ФУНКЦИЙ.
Цели: обобщить и систематизировать знания учащихся о методе интервалов, рассмотреть применение метода интервалов для непрерывных функций.
Ход урока
-
АКТУАЛИЗАЦИЯ ЗНАНИЙ
Прежде чем перейдем к изучению новой темы, давайте поработаем устно и немного подготовимся к ЕГЭ.

-
ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА
Метод интервалов для нас не является новой темой. Мы его неоднократно применяли при решении квадратных неравенств. Сегодня рассмотрим применение метода интервалов к непрерывным функциям. Данный метод рассматривают при решении неравенств вида 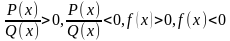 , где
, где 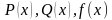 – многочлены. При этом знаки неравенств могут быть и нестрогие. Но в этом случае для дробно-рациональных неравенств нули знаменателя всегда будут исключаться из решения.
– многочлены. При этом знаки неравенств могут быть и нестрогие. Но в этом случае для дробно-рациональных неравенств нули знаменателя всегда будут исключаться из решения.
Обратите внимание, что правая часть любого из этих неравенств – число 0. Если это не задано по условию, то необходимо всё перенести в левую часть. Далее левую часть неравенства разложить на множители (если она не приведена к этому виду изначально) и найти нули каждого множителя. Необходимо помнить правило: произведение множителей равно нулю, когда хотя бы один из множителей равен нулю.
Суть этого метода рассмотрим на конкретном примере. Откройте тетради и запишите число и тему урока. А далее вместе со мной решаем примеры с записью в тетрадь.
ПРИМЕР 1. Решим неравенство 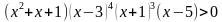 .
.
Данное неравенство изначально задано в виде произведения многочленов, а его правая часть – число 0. Значит нам остается найти нули каждого множителя, приравняв по отдельности скобки к нулю.
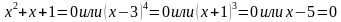
-
Рассмотрим уравнение 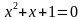 и найдем его корни. Оно не имеет решений и на всем промежутке изменения квадратный трехчлен
и найдем его корни. Оно не имеет решений и на всем промежутке изменения квадратный трехчлен 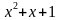 имеет положительный знак, т.е.
имеет положительный знак, т.е. 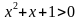 .
.
-
Рассмотрим уравнение 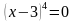 . Его корнем является число 3, при этом кратность этого корня 4. Вспомните, на что влияет четная и нечетная кратность корня.
. Его корнем является число 3, при этом кратность этого корня 4. Вспомните, на что влияет четная и нечетная кратность корня.
-
Рассмотрим уравнение 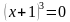 . Его корнем является число -1, кратность которого 3.
. Его корнем является число -1, кратность которого 3.
-
Рассмотрим уравнение 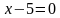 . Его корень – число 5, кратности 1.
. Его корень – число 5, кратности 1.
Т.е. нулями являются всего три числа: -1; 3; 5. Их необходимо нанести на числовую прямую. Точки будут не закрашены, ведь знак неравенства строгий.
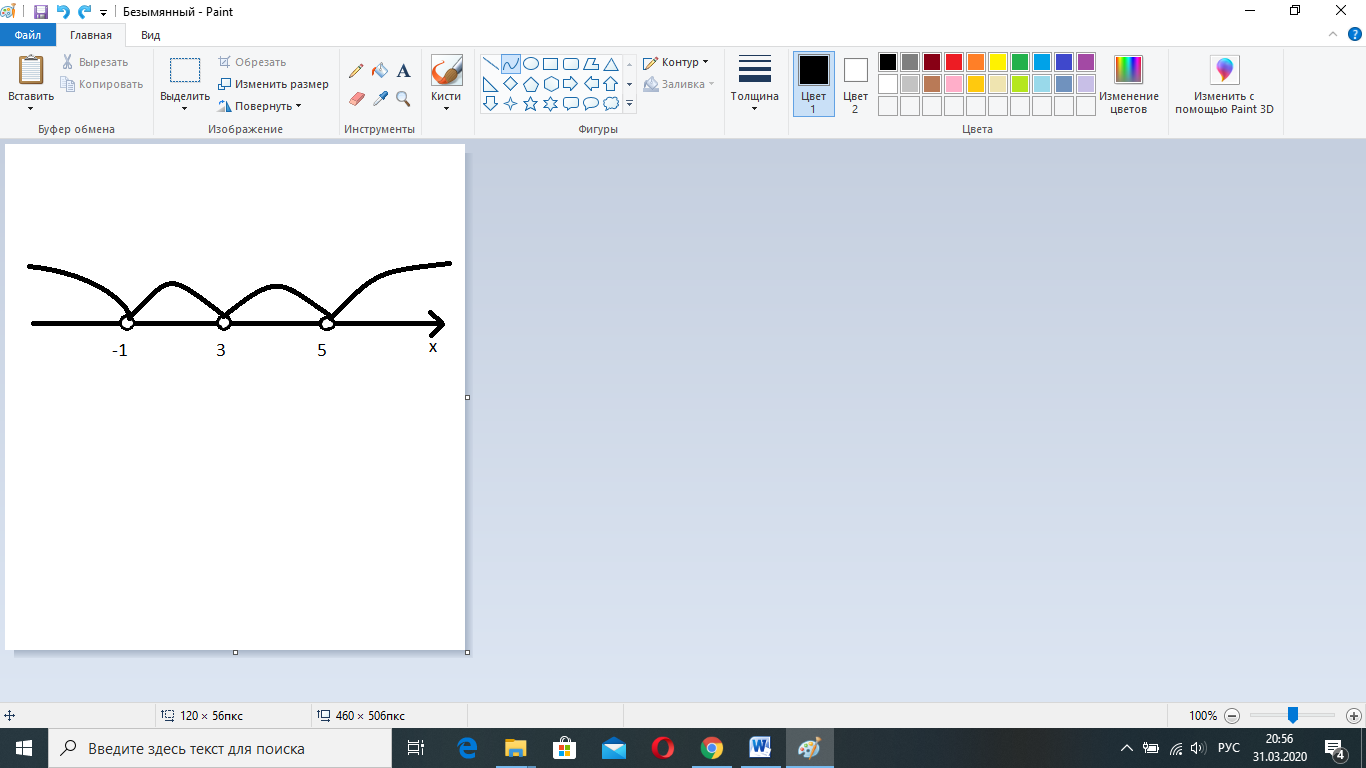
А далее необходимо определить знаки исходного неравенства на каждом интервале.
-
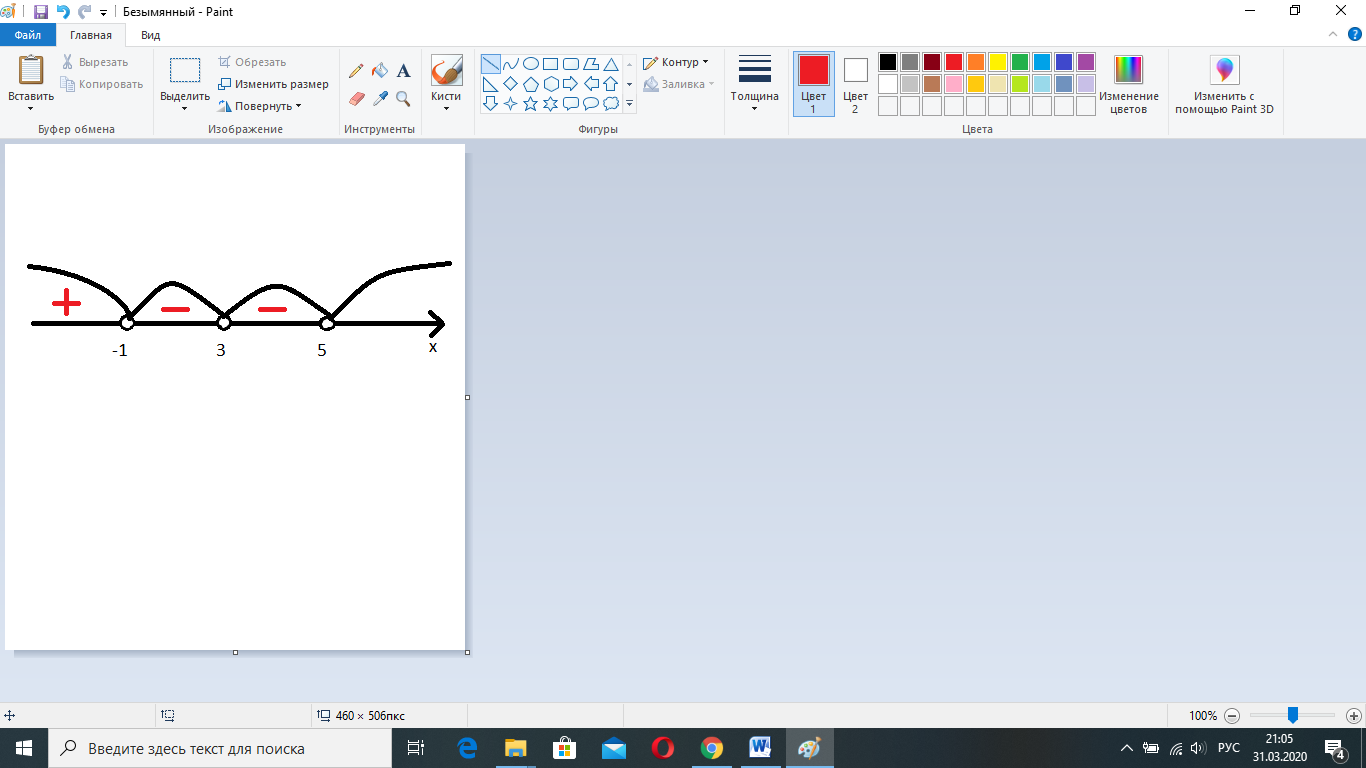
Рассмотрим интервал (-∞; -1). Выберем из этого интервала число -2 и подставим в неравенство 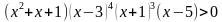 . Получим знаки (+)(+)(-)(-)=+. Отметим знак «+» на числовой прямой.
. Получим знаки (+)(+)(-)(-)=+. Отметим знак «+» на числовой прямой.
-
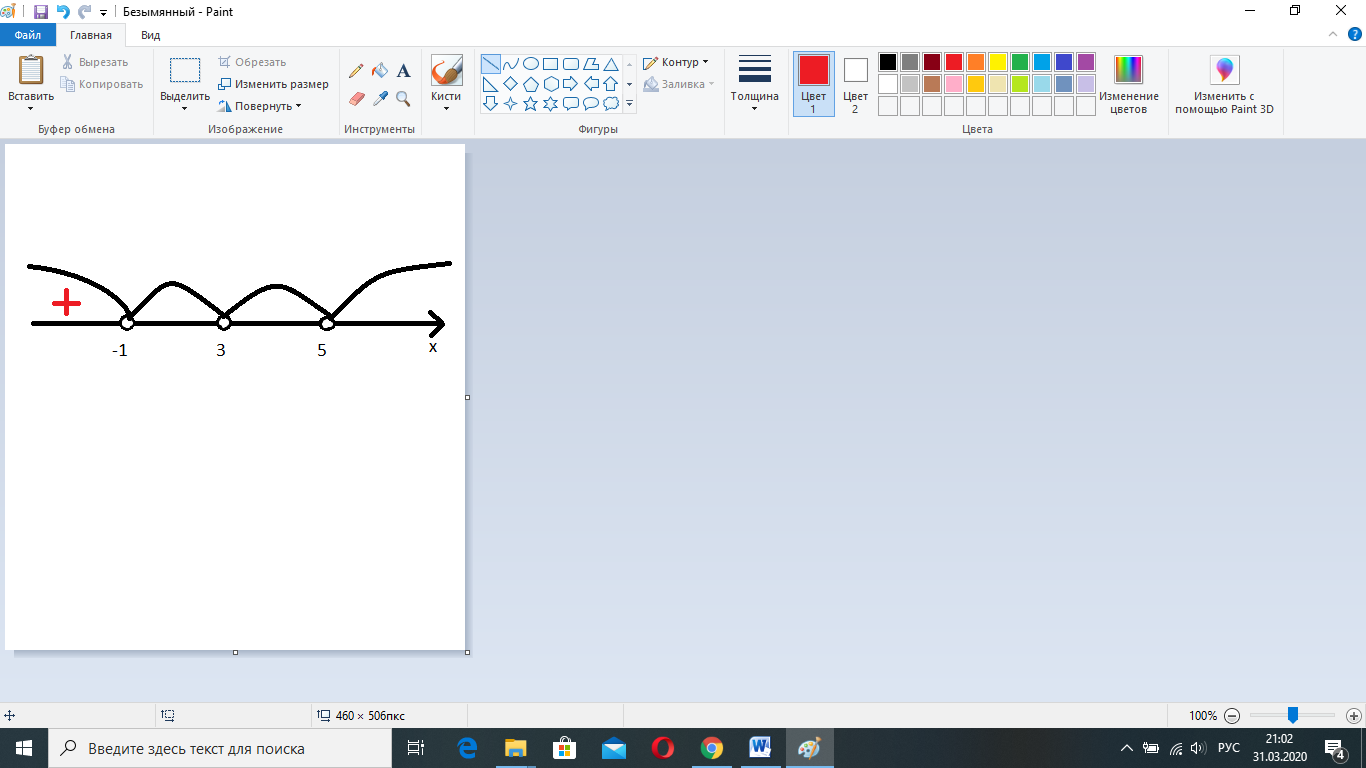
Рассмотрим интервал (-1; 3). Выберем из этого интервала число 0 и подставим в неравенство 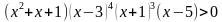 . Получим знаки (+)(+)(+)(-)=-. Отметим знак «-» на числовой прямой.
. Получим знаки (+)(+)(+)(-)=-. Отметим знак «-» на числовой прямой.
-
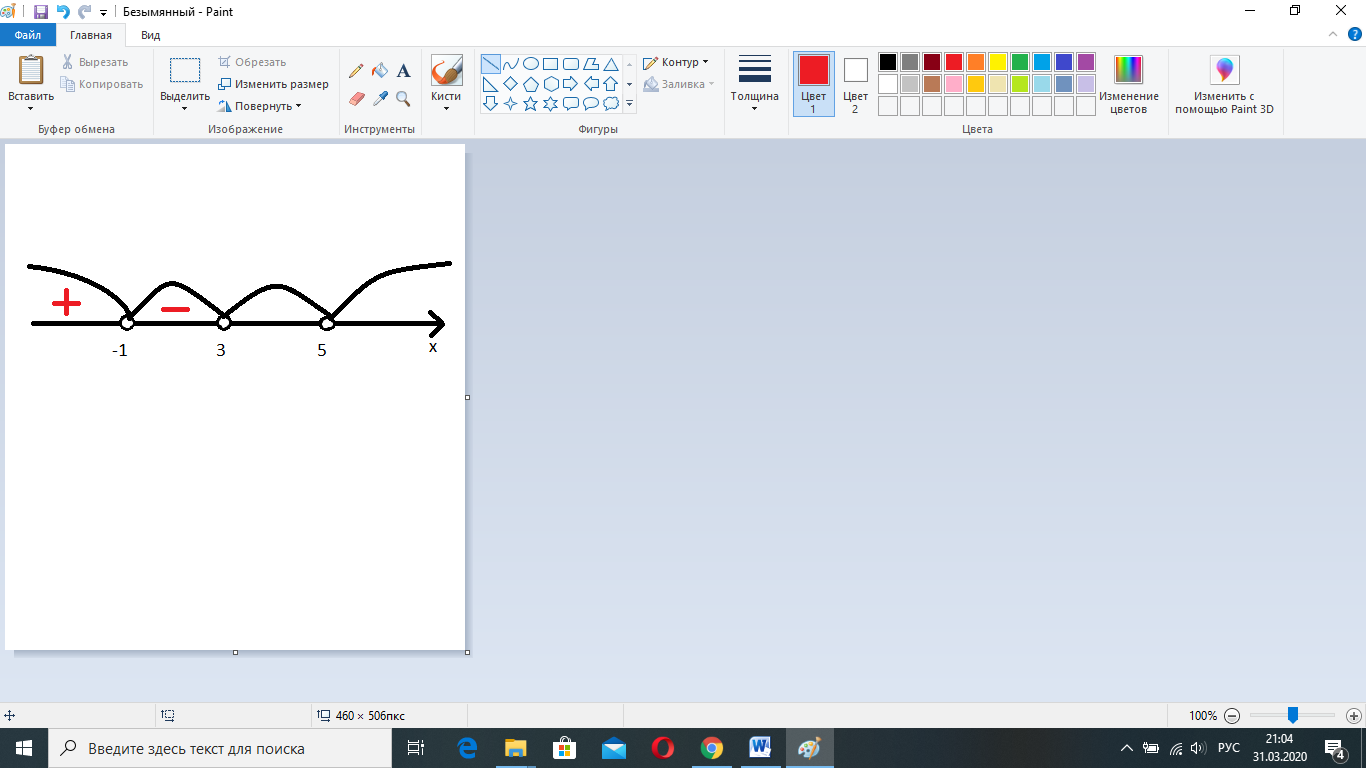
Рассмотрим интервал (3; 5). Выберем из этого интервала число 4 и подставим в неравенство 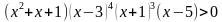 . Получим знаки (+)(+)(+)(-)=-. Отметим знак «-» на числовой прямой.
. Получим знаки (+)(+)(+)(-)=-. Отметим знак «-» на числовой прямой.
-
Рассмотрим интервал (5; +∞). Выберем из этого интервала число 6 и подставим в неравенство 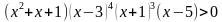 . Получим знаки (+)(+)(+)(+)=+. Отметим знак «+» на числовой прямой.
. Получим знаки (+)(+)(+)(+)=+. Отметим знак «+» на числовой прямой.
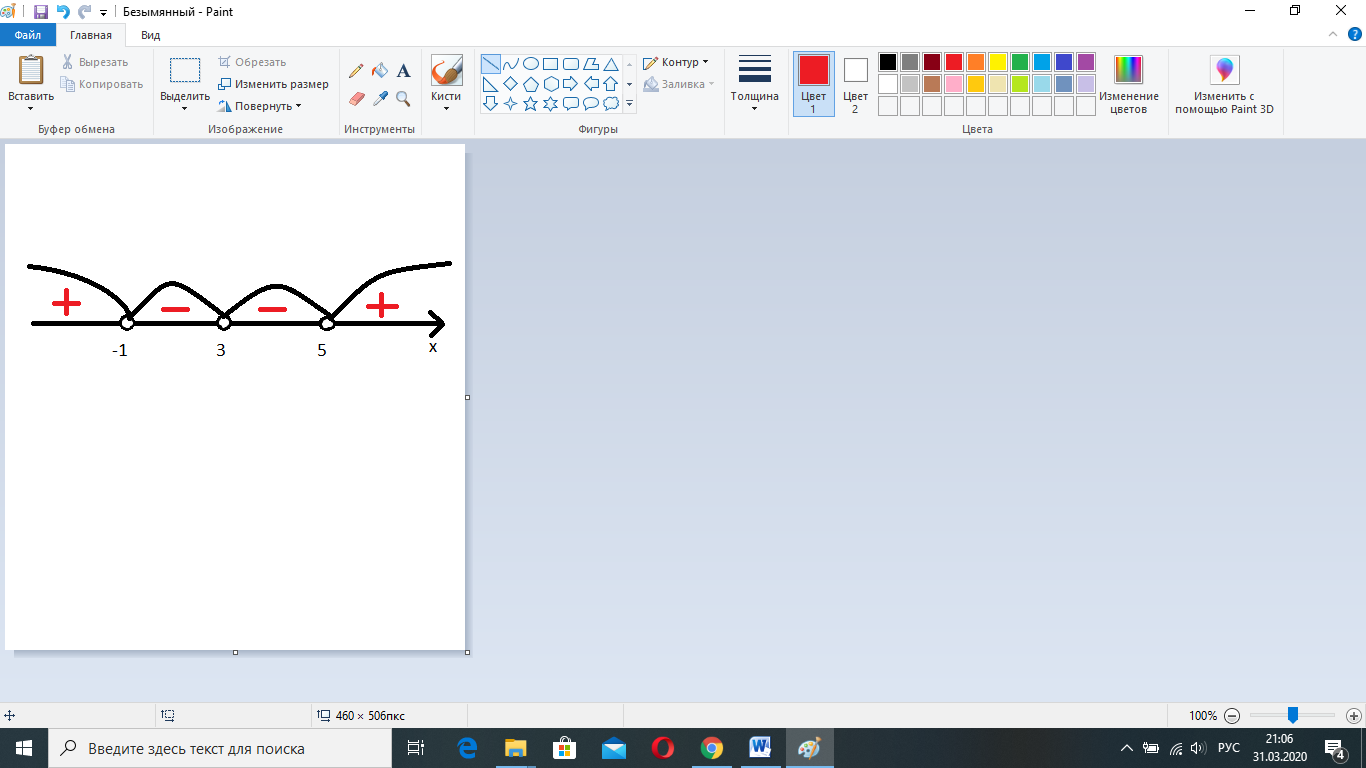
Запишем ответ к неравенству. Нам необходимо больше нуля, значит знаки «+».
Ответ: 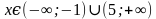 .
.
Обратите внимание. Знаки не всегда чередуются. И на чередование знаков влияет кратность корня. Если корень нечетной кратности, то знаки слева и справа от него будут чередоваться. А если корень четной кратности, то чередование не происходит, знаки слева и справа от корня будут одинаковые. Так вышло с х=3, т.к. его кратность равна 4.
ПРИМЕР 2. Решим неравенство  .
.
Правая часть – число 0, но левая не задана в виде произведения (на самом деле это не столь важно, ведь мы сможем найти отдельно нули числителя и знаменателя). Вспомним, что дробь равна нулю, если числитель равен нулю, а знаменатель не равен нулю.
-
Приравняем числитель к нулю и решим уравнение.
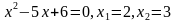 .
.
-
Рассмотрим знаменатель и найдем его нуль, который необходимо исключить из числовой прямой.
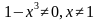 .
.
Нанесем нули числителя и нуль знаменателя на числовую прямую. Само неравенство перепишем в виде 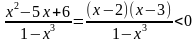 .
.
Снова определим знаки исходного неравенства на каждом интервале.
-
Рассмотрим интервал (-∞; 1). Выберем из этого интервала число 0 и подставим в неравенство . Получим знаки  . Отметим знак «+» на числовой прямой.
. Отметим знак «+» на числовой прямой.
-
Рассмотрим интервал (1; 2). Выберем из этого интервала число 1,5 и подставим в неравенство . Получим знаки  . Отметим знак «-» на числовой прямой.
. Отметим знак «-» на числовой прямой.
-
Рассмотрим интервал (2; 3). Выберем из этого интервала число 2,5 и подставим в неравенство . Получим знаки  . Отметим знак «+» на числовой прямой.
. Отметим знак «+» на числовой прямой.
-
Рассмотрим интервал (3; +∞). Выберем из этого интервала число 5 и подставим в неравенство . Получим знаки  . Отметим знак «-» на числовой прямой.
. Отметим знак «-» на числовой прямой.
Запишем ответ к неравенству. Нам необходимо меньше нуля, значит знаки «-».
Ответ: .
-
ПРАКТИЧЕСКАЯ ЧАСТЬ
Открываем учебники на странице 313 и вместе выполним №12.20(а)
№12.20(а). Решите неравенство: .
В неравенстве встретилась функция  . Она определена и непрерывна на множестве . Т.е. множество, на котором мы будем находить решение заданного неравенства, имеет вид M=[-3; 3]. При этом числа -3 и 3 являются корнями.
. Она определена и непрерывна на множестве . Т.е. множество, на котором мы будем находить решение заданного неравенства, имеет вид M=[-3; 3]. При этом числа -3 и 3 являются корнями.
Рассмотрим  . Откуда х=0 или х=4. Но х=4 не принадлежит множеству М, поэтому его на числовую прямую не наносим. Отметим на прямой числа -3; 0; 3.
. Откуда х=0 или х=4. Но х=4 не принадлежит множеству М, поэтому его на числовую прямую не наносим. Отметим на прямой числа -3; 0; 3.
Определим знаки исходного неравенства на каждом интервале.
-
Рассмотрим промежуток [-3; 0]. Выберем из этого интервала число -1 и подставим в неравенство . Получим знаки (+)(+)=+. Отметим знак «+» на числовой прямой.
-
Рассмотрим промежуток [0; 3]. Выберем из этого интервала число 2 и подставим в неравенство . Получим знаки (-)(+)=-. Отметим знак «-» на числовой прямой.
Запишем ответ к неравенству. Нам необходимо меньше или равное нуля, значит знаки «-» и сами корни, т.к. в них выполняется равенство нулю.
Ответ:  .
.
Теперь самостоятельно выполните №12.20(в).
-
Подведение итогов урока. Рефлексия
Домашнее задание:
№12.18(а, б) – обязательно для всех;
№12.21(а, б) – для тех, кто претендует на 4 и 5.








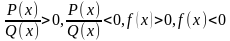 , где
, где 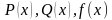 – многочлены. При этом знаки неравенств могут быть и нестрогие. Но в этом случае для дробно-рациональных неравенств нули знаменателя всегда будут исключаться из решения.
– многочлены. При этом знаки неравенств могут быть и нестрогие. Но в этом случае для дробно-рациональных неравенств нули знаменателя всегда будут исключаться из решения. 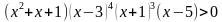 .
.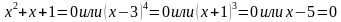
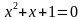 и найдем его корни. Оно не имеет решений и на всем промежутке изменения квадратный трехчлен
и найдем его корни. Оно не имеет решений и на всем промежутке изменения квадратный трехчлен 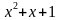 имеет положительный знак, т.е.
имеет положительный знак, т.е. 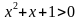 .
.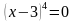 . Его корнем является число 3, при этом кратность этого корня 4. Вспомните, на что влияет четная и нечетная кратность корня.
. Его корнем является число 3, при этом кратность этого корня 4. Вспомните, на что влияет четная и нечетная кратность корня.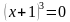 . Его корнем является число -1, кратность которого 3.
. Его корнем является число -1, кратность которого 3.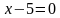 . Его корень – число 5, кратности 1.
. Его корень – число 5, кратности 1.




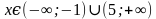 .
. .
.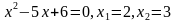 .
.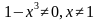 .
.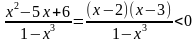 .
.