
Алгоритмы решения задач № 14 методом координат
Ежелая Е.Г.
МАОУ гимназия № 32

Шесть типов задач :
- Угол между прямыми;
- Угол между прямой и плоскостью;
- Угол между плоскостями;
- Расстояние от точки до прямой;
- Расстояние от точки до плоскости;
- Расстоя ние между прямыми.

Угол между прямыми
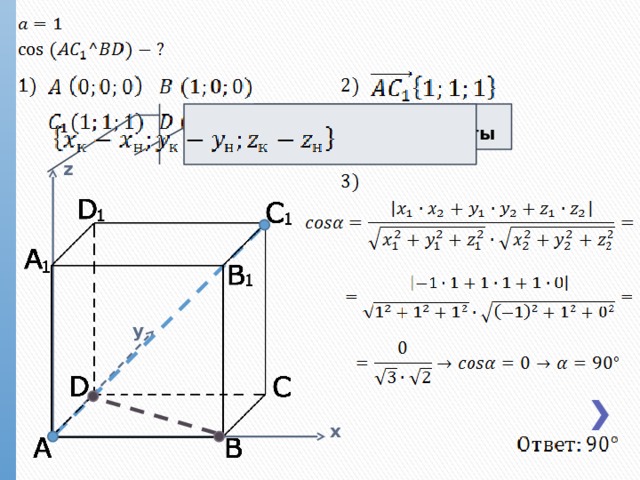
(x; y; z) – координаты точки
z
y
x

Шесть типов задач:
- Угол между прямыми;
- Угол между прямой и плоскостью;
- Угол между плоскостями;
- Расстояние от точки до прямой;
- Расстояние от точки до плоскости;
- Расстояние между прямыми.

Угол между прямой и плоскостью (метод неопределенных коэффициентов)
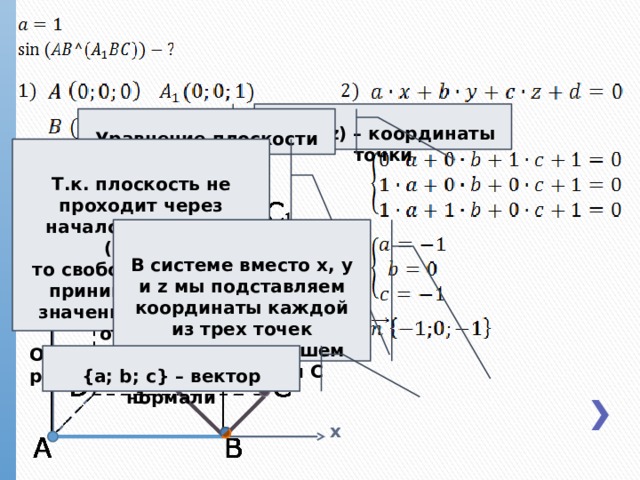
(x; y; z) – координаты точки
Уравнение плоскости
z
Т.к. плоскость не проходит через начало координат (0;0;0),
то свободный член d
принимает любое значение, отличное от нуля.
Однако для удобства расчетов мы возьмем 1
В системе вместо x, y и z мы подставляем координаты каждой из трех точек плоскости, в нашем случае A 1 , B и C
y
{a; b; c} – вектор нормали
x
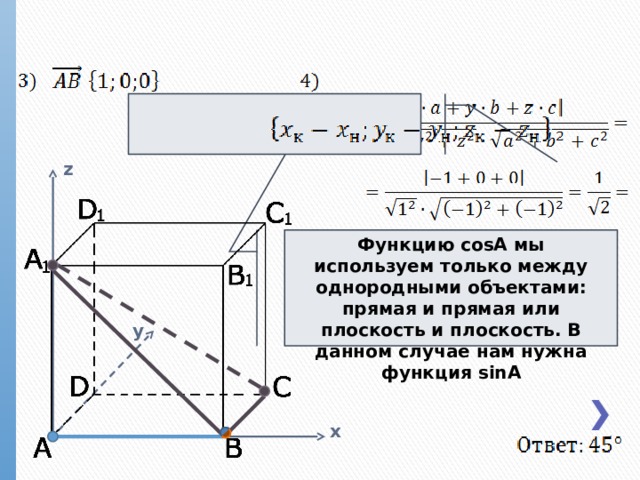
z
Функцию cosA мы используем только между однородными объектами: прямая и прямая или плоскость и плоскость. В данном случае нам нужна функция sinA
y
x

Шесть типов задач:
- Угол между прямыми;
- Угол между прямой и плоскостью;
- Угол между плоскостями;
- Расстояние от точки до прямой;
- Расстояние от точки до плоскости;
- Расстояние между прямыми.

Угол между плоскостями (метод неопределенных коэффициентов)

(x; y; z) – координаты точки
В системе вместо x, y и z мы подставляем координаты каждой из трех точек плоскости, в нашем случае A, B 1 и D
z
Уравнение плоскости
Т.к. плоскость проходит через начало координат (0;0;0),
то свободный член d
принимает значение нуля
y
{a; b; c} – вектор нормали
x
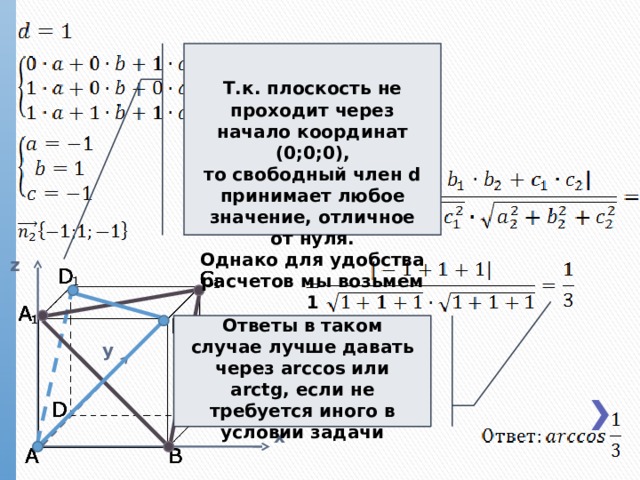
Т.к. плоскость не проходит через начало координат (0;0;0),
то свободный член d
принимает любое значение, отличное от нуля.
Однако для удобства расчетов мы возьмем 1
z
Ответы в таком случае лучше давать через arccos или arctg, если не требуется иного в условии задачи
y
x

Шесть типов задач:
- Угол между прямыми;
- Угол между прямой и плоскостью;
- Угол между плоскостями;
- Расстояние от точки до прямой;
- Расстояние от точки до плоскости;
- Расстояние между прямыми.

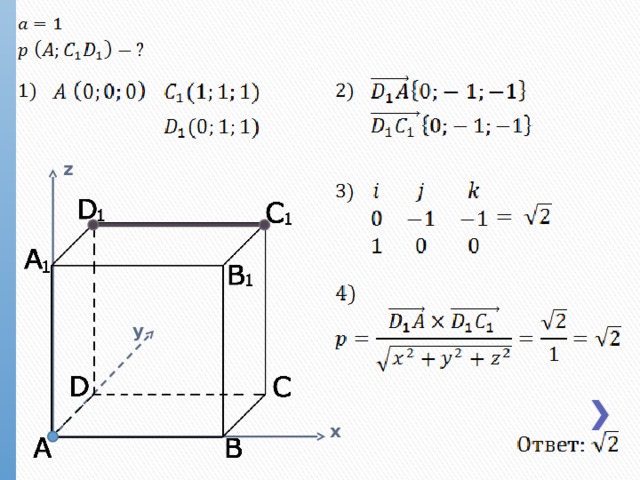
Расстояние от точки до прямой (через определители)
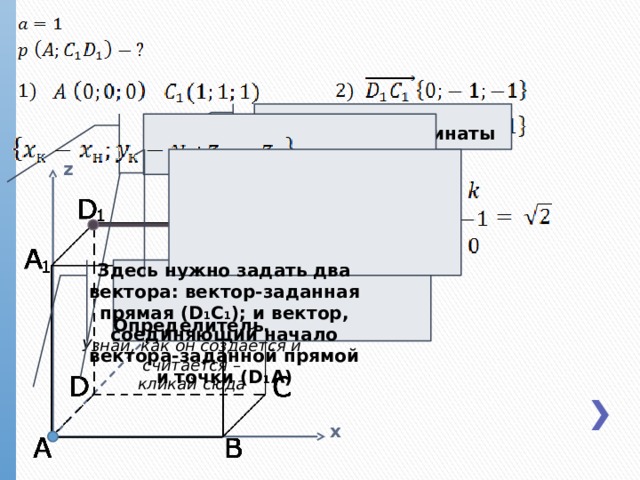
(x; y; z) – координаты точки
z
Здесь нужно задать два вектора: вектор-заданная прямая (D 1 C 1 ); и вектор, соединяющий начало вектора-заданной прямой и точки (D 1 A)
Определитель.
Узнай, как он создается и считается –
кликай сюда
y
x

Как работать с определителями (расстояние от точки до прямой)

Запомните: чтобы определить знак коэффициента i, j или k в выполнении действий с матрицами 2х2, посчитайте сумму номера строки и номера столбца: если сумма четная – знак положительный, и наоборот.
Вернуться
z
y
x

Шесть типов задач:
- Угол между прямыми;
- Угол между прямой и плоскостью;
- Угол между плоскостями;
- Расстояние от точки до прямой;
- Расстояние от точки до плоскости;
- Расстояние между прямыми.

Расстояние от точки до плоскости
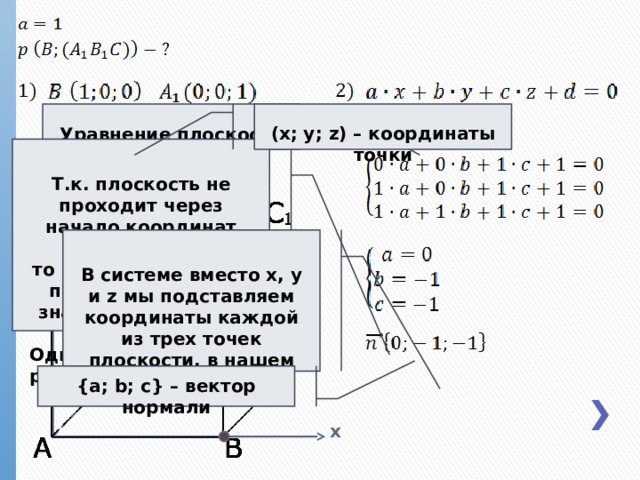
Уравнение плоскости
(x; y; z) – координаты точки
z
Т.к. плоскость не проходит через начало координат (0;0;0),
то свободный член d
принимает любое значение, отличное от нуля.
Однако для удобства расчетов мы возьмем 1
В системе вместо x, y и z мы подставляем координаты каждой из трех точек плоскости, в нашем случае A 1 , B 1 и C
y
{a; b; c} – вектор нормали
x

В числителе дроби мы записываем уравнение прямой: вектор нормали {a;b;c} перемножаем с координатами точки (x 0 ;y 0 ;z 0 ); не забываем про свободный член d, если он не равен нулю.
В знаменателе – длина вектора нормали {a;b;c}
z
y
x

Шесть типов задач:
- Угол между прямыми;
- Угол между прямой и плоскостью;
- Угол между плоскостями;
- Расстояние от точки до прямой;
- Расстояние от точки до плоскости;
- Расстояние между прямыми.

Расстояние между скрещивающимися прямыми (через определители)
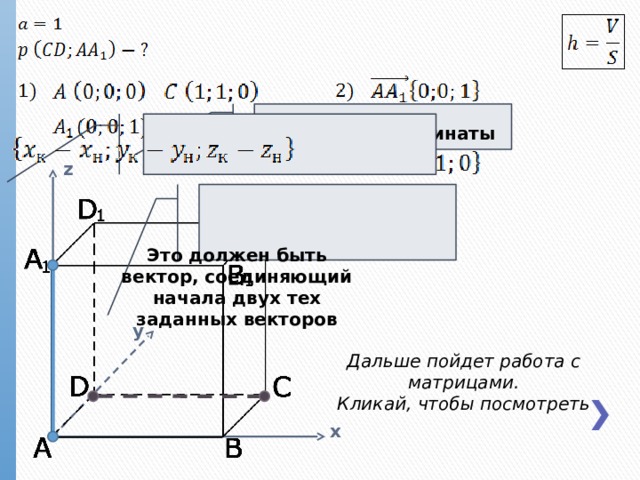
(x; y; z) – координаты точки
z
Это должен быть вектор, соединяющий начала двух тех заданных векторов
y
Дальше пойдет работа с матрицами.
Кликай, чтобы посмотреть
x

Как работать с определителями (расстояние между прямыми)

Площадь
Запомните: чтобы определить знак коэффициента i, j или k в выполнении действий с матрицами 2х2, посчитайте сумму номера строки и номера столбца: если сумма четная – знак положительный, и наоборот.

Объём
Вернуться
Запомните: чтобы определить знак коэффициента i, j или k в выполнении действий с матрицами 2х2, посчитайте сумму номера строки и номера столбца: если сумма четная – знак положительный, и наоборот.
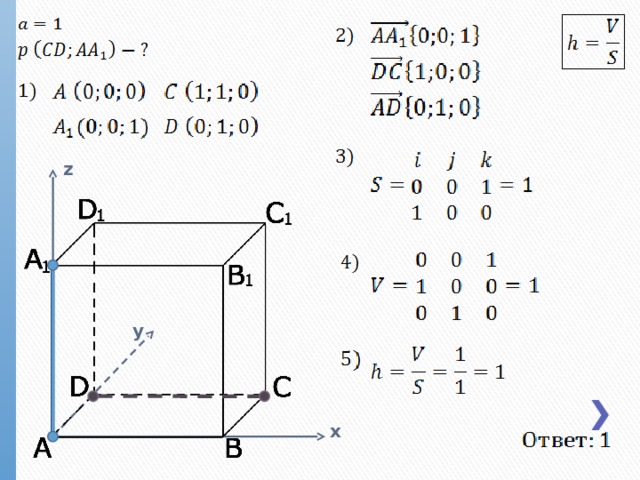
z
y
x
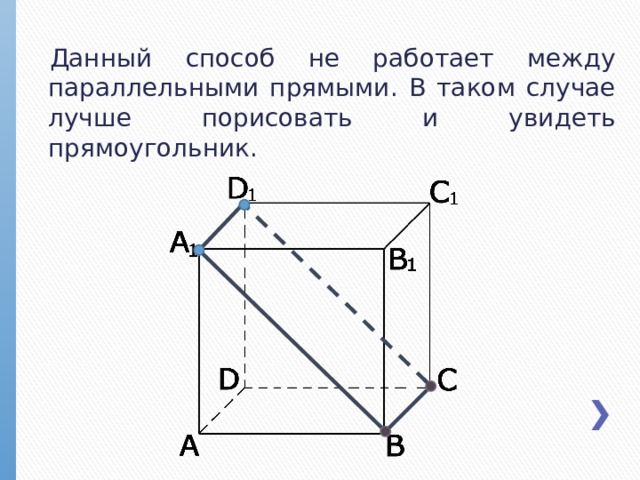
Данный способ не работает между параллельными прямыми. В таком случае лучше порисовать и увидеть прямоугольник.

Шесть типов задач:
- Угол между прямыми;
- Угол между прямой и плоскостью;
- Угол между плоскостями;
- Расстояние от точки до прямой;
- Расстояние от точки до плоскости;
- Расстояние между прямыми.
















































