Метод масс при решении геометрических задач

«Будь в моём распоряжении другая Земля, на которую можно было бы встать, я сдвинул бы с места нашу»

Архимед.

В настоящее время всё чаще приходится работать в школе над межпредметными связями. Одним из ярких примеров такой работы может стать изучение с ребятами темы «Метод масс в геометрии». Мы привыкли считать, что математика является средством изучения других наук, в том числе физики. Однако, оказывается некоторые законы физики могут стать средствами для решения математических задач.

1. Понятие центра масс и его свойства

Под материальной точкой будем понимать точку, снабженную массой. Для наглядности можно представить материальную точку в виде маленького тяжелого шарика, размерами которого можно пренебречь. Если в точке A помещена масса m, то образующую материальную точку будем обозначать так: mA. Массу m иногда называют «нагрузкой точки A».

Рассмотрим два небольших шарика, имеющих массы m1 и m2, соединённых жёстким «невесомым» стержнем. На этом стержне имеется такая точка Z, что если подвесить всю систему в этой точке, то она будет в равновесии – ни один из шариков не «перетянет». Эта точка Z и есть центр масс двух рассматриваемых материальных точек с массами m1 и m2.

При применении этого понятия к решению геометрических задач используются следующие свойства центра масс:

1. Всякая система, состоящая из конечного числа материальных точек, имеет центр масс и притом единственный.

2. Если массу каждой точки системы умножить на одно и то же положительное число, то есть уменьшить или увеличить одновременно в одинаковое число раз, то центр масс не изменится.

3. Центр масс двух материальных точек расположен на отрезке, соединяющем эти точки; его положение определяется архимедовым правилом рычага. Произведение массы материальной точки на расстояние от неё до центра масс одинаково для обеих точек, т.е. m₁d₁ = m₂d₂, где m₁, m₂ – массы материальных точек, а d₁, d₂ – соответствующие плечи, т. е. расстояния от материальных точек до центра масс.

4. Если систему материальных точек с центром масс в точке Z разбить на несколько непересекающихся подсистем и нагрузить центр масс каждой подсистемы суммарной массой соответствующей подсистемы, а затем рассмотреть систему из образованных таким образом материальных точек, то центр масс этой подсистемы совпадает с точкой Z.

5. Если в системе, состоящей из конечного числа материальных точек, отметить несколько материальных точек и массы всех отмеченных точек перенести в их центр масс, то от этого положение центра масс всей системы не изменится.

Не смотря на простоту этих фактов, они, тем не менее, представляют собой мощное средство доказательства теорем и решения геометрических задач.

2. Задачи

1) В треугольнике АВС проведена медиана ВМ. Отрезок AN делит сторону ВС в отношении 1:2 считая от вершины В. AN пересекается с ВМ в точке О. Найти отношение ОВ к ОМ.

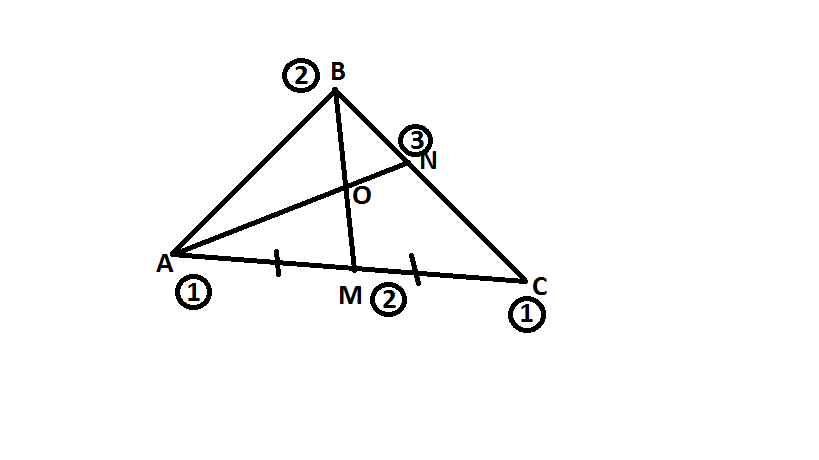Идея решения состоит в размещении в точках А, С, В таких масс, чтобы центром этих трёх масс оказалась точка О. Ясно, что в А и C надо поместить равные массы, так как тогда центром масс этих двух м. т. будет точка М, и потому, поместив надлежащую массу в точку В, можно будет добиться, чтобы центром масс всех трёх м. т. была нужная нам точка отрезка ВМ (а именно, точка О).

Итак, поместим в каждую из точек А, C массу 1, т. е. возьмём м. т. 1А, 1C. Так как BN:NC=1:2, то масса в точке В равна 2. Имеем три материальные точки: 1А, 2В и 1С. Масса в точке М равна сумме масс в точках А и С, т.е. мы имеем ее одну м.т. 2М. Так как м ассы в точках В и М равны, то ВО:ОМ= 2:2=1:1(По правилу рычага).

Ответ: 1:1;

2) В треугольнике АВС точка М- середина АС. Точка К делит АВ как 2:1 считая от вершины А. Точка Р делит ВС в отношении 2:1 от вершины В. КР пересекается с ВМ в точке О. В каком отношении точка О делит отрезок КР

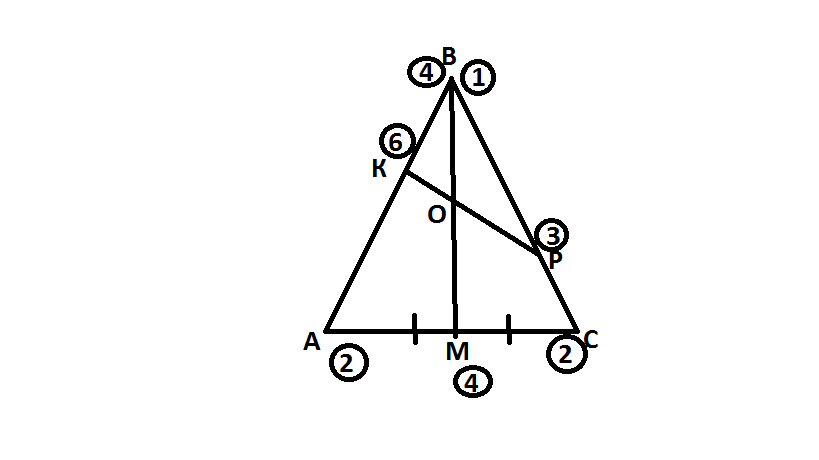
Идея решения состоит в размещении в точках М, В, К и Р таких масс, чтобы центром этих четырех масс оказалась точка О. Ясно, что в А и C надо поместить равные массы, так как тогда центром масс этих двух м. т. будет точка М, и потому, поместив надлежащую массу в точку В, можно будет добиться, чтобы центром масс всех трёх м. т. была нужная нам точка отрезка ВМ (а именно, точка О).

Итак, поместим в каждую из точек А, C массу 2, т. е. возьмём м. т. 2А, 2C. Следовательно в точке М масса будет равна 4. Так как АК:КВ= 2:1, то масса в точке В будет равна 4. Но есть еще один случай: так как ВР:РС=2:1, то масса в точке В будет равна 1. Следовательно получаем материальные точки 4В и 1В. Масса в точке К равна 6(2А+4В), а масса в точке Р равна 3(2С+1В). Т. О- центр масс треугольника АВС. По правилу рычага находим отношение КО к ОР- КО:ОР=3:6=1:2.

Ответ: 1:2;

3. Задачи для самостоятельного решения

1. В треугольнике АВС проведена медиана ВМ. На стороне ВС взята точка N. AN пересекается с ВМ в точке О. Найти отношение ОВ к ОМ, если а) ВN:NC=1:2 б) ВN:NC=3:2.

Ответ: а) 1:1, б) 1:3

1. В треугольнике ABC точка к делит сторону BC в отношении 1:4, считая от вершины B. В каком отношении отрезок AK делит медиану BM? Ответ: 1:2

1. На стороне BC треугольника ABC взята точка N такая, что 3BN = CN. В каком отношении прямая AN делит медиану BM ? Ответ: 3:2

2. В треугольнике АВС проведены чевианы ВМ и АN так, что ВN: NC=1:5, а АМ: МС=1:2. Найти ВО:ОМ и АО:ON, где О - точка пересечения чевиан. Ответ: ВО:ОМ=3:5, АО:ОN=6:2=3:1

4. Метод масс (ГИА и ЕГЭ)

1. В треугольнике АВС проведена медиана ВМ. Отрезок AN делит сторону ВС в отношении 1:2 считая от вершины В. AN пересекается с ВМ в точке О. Найти отношение ОВ к ОМ. Ответ: 1:1

1. В треугольнике АВС точка М- середина АС. Точка К делит АВ как 2:1 считая от вершины А. Точка Р делит ВС в отношении 2:1 от вершины В. КР пересекается с ВМ в точке О. В каком отношении точка О делит отрезок КР? Ответ: 1:2

1. Площадь треугольника ABC равна 40, биссектриса AD пересекает медиану BK в точке E, при этом BD : CD = 3 : 2. Найдите площадь четырехугольника EDCK. Ответ: 11

1. Площадь треугольника АВС равна 80. Биссектриса AD пересекает медиану BK в точке E при этом BD:CD=1:3. найдите площадь четырехугольника EDCK. Ответ: 36

1. Дан треугольник АВС. BD- чевиана. На стороне АВ лежит точка М, на стороне ВС- точка Р, на стороне АС- точка D так, что АМ/МВ= 4/3, ВР/РС=2/1, AD/DC=5/7. Прямые BD и МР пересекаются в точке К. Найти отношения ВК/КD и МК/КР. Ответ: 45:98, 72:71;

1. Биссектриса угла B треугольника ABC делит медиану , проведенную из вершины C, в отношении 7:2, считая от вершины C. В каком отношении, считая от вершины A, эта биссектриса делит медиану, проведенную из вершины A? Ответ: 7:8

1. Точка A₁ симметрична вершине A треугольника ABC относительно середины стороны BC, точка B₁ симметрична вершине B относительно середины стороны AC. Докажите, что точки A₁, B₁ и C лежат на одной прямой.

1. Дан прямоугольный треугольник АВС, с катетами АВ и ВС(АВ=5, ВС=12). Пусть точка I-центр окружности, вписанной в треугольник АВС. Прямая, проходящая через точку I, параллельна одной из сторон треугольника АВС и пересекает две другие стороны в точках К и Р. Найдите длину отрезка КР. Ответ: 221/30, 36/5,25/6;

1. В треугольнике ABC точка K лежит на стороне BC так, что BK : KC = 1 : 2, биссектриса CM пересекается с прямой AK в точке L, при этом AM : MB = 1:4. Найдите площадь треугольника ABC, если площадь четырехугольника MBKL равна 52. Ответ: 165

1. Площадь треугольника ABC равна 120, точка D лежит на отрезке BC так, что BD : CD = 1 : 2, биссектриса BK пересекает прямую AD в точке L. Найдите площадь четырехугольника KLDC, если AK : KC = 3 : 1. Ответ: 1,25

1. В треугольнике АВС из вершин А и В проведены отрезки АК и ВЕ, причем точки К и Е лежат на сторонах ВС и АС соответственно. Отрезки АК и ВЕ пересекаются в точке М так, что АМ : МК = 5, ВМ : МЕ = 2. Найдите отношения АЕ : ЕС и ВК : КС.

Ответ: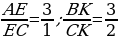

12. (Ларин 354)

Медиана ВМ и биссектриса АР треугольника АВС пересекаются в точке К, длина стороны АС втрое больше длины стороны АВ. Найдите отношение площади треугольника АВК к площади четырёхугольника КРСМ.

Ответ: 1/8.