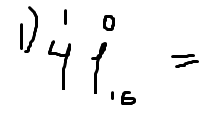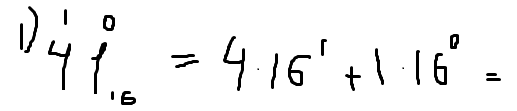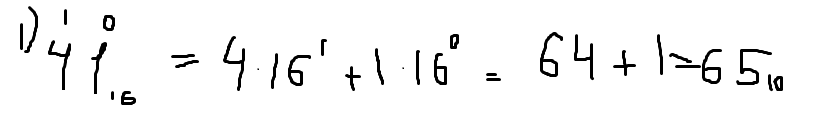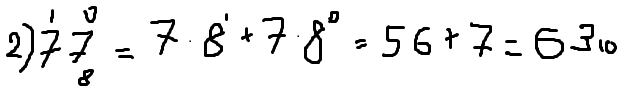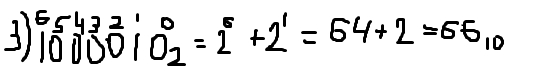Метод решения 10-го задания ЕГЭ: системы счисления

10-е задание – последнее задание из первой письменной части. 10-е задние на систему счисления и на сравнение чисел в разных системах счисления.

1. Задание 10 представляет из себя перевод чисел из любой системы счисления в десятичную, и из десятичной системы счисления в любую другую систему счисления, а также перевод из одной системы счисления в другую через десятичную систему счисления. Попробуем разобраться с заданием 10 с помощью примера:

Пример

Что мы видим? У нас есть 3 числа. Маленькие циферки справа внизу показывают, что это число записано в данной системе счисления. Т.Е. 41 – в шестнадцатеричной, 77 – в восьмеричной, 1000010 – в двоичной. Нам нужно найти минимальное.

По идее, мы должны все эти числа перевести в какую-то одну систему счисления (Далее – СС), и их сравнить. Но! Нам здесь ответ нужно дать в десятичной СС. Сравнивать будет удобнее, кстати, в десятичной СС. Поэтому и все данное задание сводится к тому, что мы просто должны перевести все эти числа в десятичную СС. И таким образом найти, какое же из них будет самое маленькое.

И так, поехали!

Первое число – 41 в шестнадцатеричной СС. Как же осуществляется перевод? Мы справа налево, начиная с нуля, номеруем разряды каждой циферки. То есть 0 –1. Если бы у меня здесь были еще какие-то цифры, то это было бы: 0,1,2,3,4 и тд.

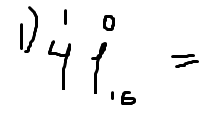
Далее, что мы делаем, мы берем каждую цифру данного числа, умножаем на основание СС, то есть на ту СС, из которой мы переводим, в нашем случае шестнадцатеричная, в той степени, которая стоит над данной цифрой. Как это будет? 4 я умножаю на 16. Какая здесь стоит степень? Да, первая. То есть на 16 в первой степени.

И так я делаю с каждой цифрой, а потом все это дело суммирую.Т.е. дальше у меня получается 1*16 в нулевой степени. Все. Теперь нам осталось просто посчитать, и полученное число и будет являться переводом этого числа в десятичную СС.

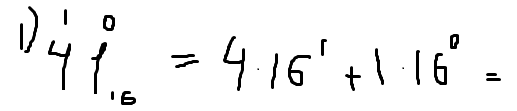
Итак, 4*16^1+1*16^0=64+1=65(в десятичной СС)

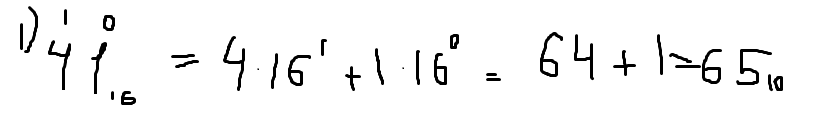
С первым числом разобрались.

Второе число по такому-же принципу.

77 в восьмеричной переводим в десятеричную СС.

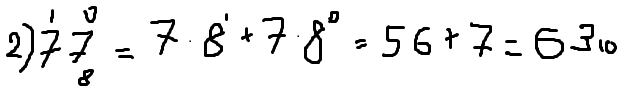
И последнее 3 число:

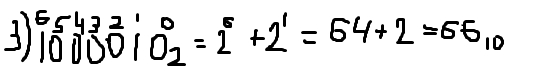
Так, тут сразу видно какое число будет минимальным. Это число 63. В ответ нужно писать число 63 без основания СС. Маленькую «10» писать не надо.

Для перевода чисел из десятичной системы счисления в любую другую, необходимо целочисленно делить переводимое число на основание той системы, в которую мы хотим его перевести, до тех пор пока результат целочисленного деления не станет равен 0. Результатом перевода будут цифры остатка от каждого деления, в обратном порядке.

Примеры перевода чисел из десятичной системы счисления:

•43(в десятичной СС) перевести в двоичную систему счисления:

43/2 = 21 и 1 в остатке

21/2 = 10 и 1 в остатке

10/2 = 5 и 0 в остатке

5/2 = 2 и 1 в остатке

2/2 = 1 и 0 в остатке

1/2 = 0 и 1 в остатке

результат - цифры остатков в обратном порядке = 101011(в двоичной СС)

•751(в десятичной СС) перевести в восьмеричную систему счисления:

751/8 = 93 и 7 в остатке

93/8 = 11 и 5 в остатке

11/8 = 1 и 3 в остатке

1/8 = 0 и 1 в остатке

результат - цифры остатков в обратном порядке = 1357(в восьмеричной СС)

•15305(в десятичной СС) перевести в шестнадцатеричную систему счисления:

15305/16 = 956 и 9 в остатке

956/16 = 59 и 12 в остатке - соответствует цифре C (в шестнадцатеричной СС)

59/16 = 3 и 11 в остатке - соответствует цифре В (в шестнадцатеричной СС)

3/16 = 0 и 3 в остатке

результат - цифры остатков в обратном порядке = 3BC9 (в шестнадцатеричной СС)