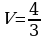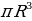9 класс Тема 2 Метод координат Геометрия
1.Сформулируйте и докажите лемму о коллинеарных векторах (если векторы  и
и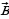 коллинеарны и
коллинеарны и
 ≠ 0 , то существует такое число k
≠ 0 , то существует такое число k 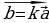 )
)
2.Что значит разложить вектор по двум данным векторам? (если вектор 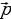 = х
= х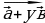 , где х и у некоторые числа , то говорят , что вектор
, где х и у некоторые числа , то говорят , что вектор 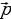 разложен по векторам
разложен по векторам  и
и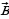 , числа х и у называют коэффициентами разложения)
, числа х и у называют коэффициентами разложения)
3.Сформулируйте теорему о разложении вектора по двум неколлинеарным векторам ( на плоскости любой вектор можно разложить по двум данным неколлинеарным векторам, при чём коэффициенты разложения определяются единственным образом)
4.Объясните , как вводится прямоугольная система координат
5.Что такое координатные векторы (векторы 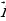 и
и  называются координатными векторами)
называются координатными векторами)
6.Что такое координаты вектора ( коэффициенты разложения вектора 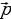 по координатным векторам называются координатами вектора
по координатным векторам называются координатами вектора 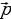 в данной системе координат)
в данной системе координат)
7.Как связаны между собой координаты равных векторов ( координаты равных векторов соответственно равны).
8.Сформулируйте и докажите правила нахождения координат суммы и разности векторов:
1. каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов.
2. каждая координата разности двух векторов равна разности соответствующих координат этих векторов.
9. Сформулируйте и докажите правила нахождения координат произведения вектора на число по заданным координатам вектора ( каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число).
10.Как выразить координаты вектора через координаты его начала и конца (каждая координата вектора равна разности соответствующих координат его конца и начала) 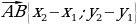
11.Вычисление координат середины отрезка по координатам его концов ( каждая координата середины отрезка равна полусумме соответствующих координат его концов)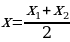
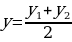 .
.
12.Вычисление длины вектора по его координатам ( 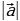 =
=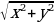 ).
).
13.Вычисление расстояния между двумя точками по их координатам ( d =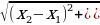 ).
).
14.Какое уравнение называется уравнением данной линии ( уравнение с двумя переменными х и у
называется уравнением линии ℓ, если этому уравнению удовлетворяют координаты любой точки линии ℓ и не удовлетворяют координаты никакой точки, не лежащей на этой линии)
15.Выведите уравнение окружности данного радиуса с центром в данной точке в прямоугольной системе координат уравнение окружности радиуса r с центром в точке С ( ) имеет вид:
) имеет вид:
 =
=
16. Уравнение окружности радиуса r с центром в начале координат имеет вид: 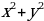 =
= 
17.Выведите уравнение данной прямой в прямоугольной системе координат (ax + by + c = 0 – уравнение прямой в прямоугольной системе координат является уравнением первой степени).
18. Что такое угловой коэффициент прямой ( если в уравнении прямой коэффициент b отличен от нуля , то уравнение прямой можно записать так : y = kx+d, k =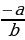 , d =
, d =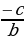 . Число k называется угловым коэффициентом прямой)
. Число k называется угловым коэффициентом прямой)
19.Когда две прямые параллельны ( если две прямые имеют одинаковые угловые коэффициенты , то эти прямые параллельны)
20.Напишите уравнение прямых, проходящих через данную точку М0 ( х0; у0 ) и параллельных осям координат ( х = х0 , у = у0).
21.Напишите уравнение осей координат ( ось Ох имеет уравнение у = 0, а ось Оу – уравнение х = 0)
22. Взаимное расположение двух окружностей с радиусами r и R и расстоянием d между их центрами :
1. Если центры окружностей совпадают , т.е. d = 0, r  R , то окружности называются концентрическими, и окружность радиуса r лежит внутри круга радиуса R .
R , то окружности называются концентрическими, и окружность радиуса r лежит внутри круга радиуса R .
2. – одна окружность лежит внутри другой 3.
– одна окружность лежит внутри другой 3.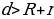 – одна окружность лежит вне другой 4.
– одна окружность лежит вне другой 4.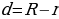 – окружности касаются изнутри 5.
– окружности касаются изнутри 5.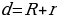 - окружности касаются извне 6.
- окружности касаются извне 6.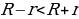 – окружности пересекаются в двух точках
– окружности пересекаются в двух точках
9 класс Тема 3 Векторы Геометрия
1.Дайте определение вектора (отрезок , для которого указано , какая из его граничных точек считается началом, а какая – концом , называется направленным отрезком или вектором).
2.Какой вектор называется нулевым ( если начало вектора совпадает с его концом , то такой вектор называется нулевым)
3. Чему равна длина нулевого вектора (длина нулевого вектора считается равной нулю:  0).
0).
4.Что называется длиной ненулевого вектора ( длиной или модулем ненулевого вектора 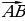 называется длина отрезка АВ . длина вектора
называется длина отрезка АВ . длина вектора 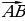 (вектора
(вектора  ) обозначается так:
) обозначается так: 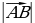 (
(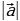 )).
)).
5.Какие векторы называются коллинеарными ( ненулевые векторы называются коллинеарными, если они лежат либо на одной прямой , либо на параллельных прямых; нулевой вектор считается коллинеарным любому вектору)
6. Изобразите на рисунке сонаправленные векторы и
и 
 и противоположно направленные векторы
и противоположно направленные векторы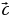 и
и 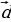 . (
. (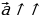
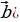 - обозначение сонаправленных векторов, (
- обозначение сонаправленных векторов, ( ) - противоположно направленные вектора
) - противоположно направленные вектора
7.Дайте определение равных векторов ( векторы называется равными, если они сонаправлены и их длины равны).
8.Объясните, какой вектор называется суммой двух векторов. В чём заключается правило треугольника сложения двух векторов ( сумма векторов  и
и  обозначается так:
обозначается так:  +
+ Правило треугольника можно сформулировать следующим образом: если А, В и С – произвольные точки , то
Правило треугольника можно сформулировать следующим образом: если А, В и С – произвольные точки , то 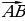 +
+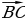 =
= 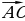 )
)
9.Правило сложения с нулевым вектором ( для любого вектора справедливо равенство
справедливо равенство  +
+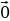 =
= )
)
10. Законы сложения векторов: для любых векторов  ,
,  и
и 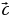 справедливы равенства :
справедливы равенства :
1. +
+ =
= +
+ - переместительный закон
- переместительный закон
2.(  +
+ ) +
) +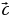 =
=  + (
+ ( – сочетательный закон.
– сочетательный закон.
11. В чём заключается правило параллелограмма сложения двух неколлинеарных векторов 12. Какой вектор называется разностью двух векторов (разностью векторов  и
и  называется такой вектор, сумма которого с вектором
называется такой вектор, сумма которого с вектором равна вектору
равна вектору , разность векторов
, разность векторов  и
и  обозначается так:
обозначается так:  -
- ).
).
13.Какой вектор называется противоположный данному( вектор 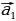 называется противоположный вектору
называется противоположный вектору  , если векторы
, если векторы  и
и 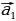 имеют равные длины и противоположно направлены.
имеют равные длины и противоположно направлены.
14. Сформулируйте и докажите теорему о разности векторов (для любых векторов  и
и  справедливо равенство:.
справедливо равенство:. -
- =
= +(-
+(-  )).
)).
15.Какой вектор называется произведением данного вектора на данное число ( произведением ненулевого вектора  на число k называется такой вектор
на число k называется такой вектор  , длина которого равна
, длина которого равна 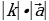 причём векторы
причём векторы  и
и сонаправлены при k
сонаправлены при k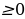 и противоположно направлены при k
и противоположно направлены при k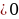 . Произведение нулевого вектора на любое число считается нулевой вектор).
. Произведение нулевого вектора на любое число считается нулевой вектор).
16. Чему равно произведение k  ,если :
,если : 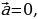 k = 0 (произведение любого вектора на число нуль есть нулевой вектор)
k = 0 (произведение любого вектора на число нуль есть нулевой вектор)
17.Могут ли векторы  и k
и k  , быть неколлинеарными (для любого числа k и любого вектора
, быть неколлинеарными (для любого числа k и любого вектора  и k
и k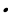
 коллинеарны).
коллинеарны).
18. Сформулируйте основные свойства умножение вектора на число( для любых чисел k, m и любых векторов  ,
,  справедливы равенства:
справедливы равенства:
1.( k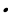 m)
m)  = k (m
= k (m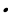
 ) – сочетательный закон
) – сочетательный закон
2. ( k + m )  = k
= k  + m
+ m  – первый распределительный закон
– первый распределительный закон
3. k ( +
+  ) = k
) = k  + k
+ k - второй распределительный закон
- второй распределительный закон
19. Какой отрезок называется средней линией трапеции (средней линией трапеции называется отрезок, соединяющий середины её боковых сторон)
20.Сформулируйте и докажите теорему о средней линии трапеции (средняя линия трапеции параллельна основаниям и равна их полусумме)
9 класс Тема 4 Соотношения между сторонами и углами треугольника. Геометрия Скалярное произведение векторов
1.Начертите оси координат и постройте единичную полуокружность.
2.Объясните , что такое синус косинус угла 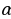 из промежутка
из промежутка 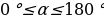 (для любого угла
(для любого угла 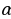 из промежутка
из промежутка 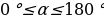 синусом называется ордината у точки М , а косинусом угла
синусом называется ордината у точки М , а косинусом угла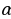 - абсциссе х точки М, 0
- абсциссе х точки М, 0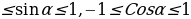 )
) 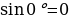 ,
, 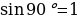 .
. 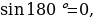
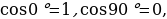
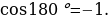
3. Что называется тангенсом угла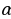 ? Для какого значения
? Для какого значения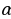 тангенс не определён и почему? (тангенсом угла
тангенс не определён и почему? (тангенсом угла 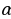 (
( 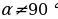 ) называется отношение
) называется отношение 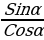 , т.е.
, т.е. 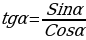 . При
. При 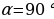
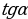 не определён , поскольку
не определён , поскольку 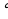 Cos 90 =0 и в формуле знаменатель обращается в нуль. Используя формулы , находим:
Cos 90 =0 и в формуле знаменатель обращается в нуль. Используя формулы , находим: 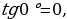
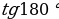 = 0 ).
= 0 ).
4. Что называется котангенсом угла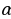 ? Для какого значения
? Для какого значения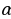 котангенс не определён и почему? ( котангенсом угла
котангенс не определён и почему? ( котангенсом угла 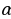 (
(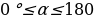 ) называется отношение
) называется отношение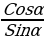 , т.е.
, т.е.  . При
. При 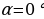 и
и 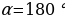
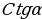 не определён. Исходя из формул
не определён. Исходя из формул 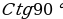 = 0).
= 0).
5. Докажите основное тригонометрическое тождество ( 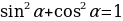 )
)
6. Напишите формулы приведения:
при 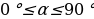
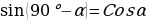 , Cos (
, Cos (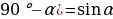 .
.
при 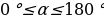
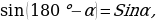

7 .Сформулируйте и докажите теорему о площади треугольника( вычисление площади треугольника по двум сторонам и углу между ними)-
.Сформулируйте и докажите теорему о площади треугольника( вычисление площади треугольника по двум сторонам и углу между ними)-
площадь треугольника равна половине произведения двух его сторон на синус угла между ними 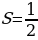 absin C
absin C
8.Сформулируйте и докажите теорему синусов( стороны треугольника пропорциональны синусам противоположных углов 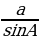 =
=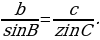 Замечание к теореме синусов (
Замечание к теореме синусов (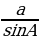 =
=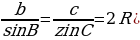
9 . Сформулируйте и докажите теорему косинусов ( квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними) -
. Сформулируйте и докажите теорему косинусов ( квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними) - 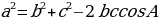
10.Что означают слова « решение треугольника» ? Сформулируйте трт основные задачи на решение треугольников и объясните, как они решаются.( решением треугольника называется нахождение всех его шести элементов ( т.е. трёх сторон, трёх углов) по каким – нибудьтрём данным элементам, определяющим треугольник).
Задача 1:решение треугольника по двум сторонам и углу между ними.
Задача 2:решение треугольника по стороне и прилежащим к ней углам.
Задача 3:решение треугольника по трём сторонам.
11. Объясните , как определить высоту предмета, основание которого недоступно.
12. Объясните , как измерить расстояние до недоступной точки.
13Объясните, что означают слова « угол между векторами  и
и  равен
равен 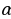 ( векторы
( векторы  и
и  не являются сонаправленными и отложены от произвольной точки , тогда градусную меру этого угла обозначим буквой
не являются сонаправленными и отложены от произвольной точки , тогда градусную меру этого угла обозначим буквой 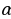 и будем говорить« угол между векторами
и будем говорить« угол между векторами  и
и  равен
равен 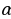 ). Если векторы
). Если векторы  и
и  сонаправлены , в частности один из них или оба нулевые, то угол между векторами
сонаправлены , в частности один из них или оба нулевые, то угол между векторами и
и  равен 0
равен 0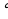 .)
.)
14. Как обозначается угол между векторами (угол между векторами и
и  обозначается так
обозначается так 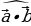
15. Какие два вектора называются перпендикулярными ( два вектора называются перпендикулярными, если угол между ними равен 90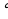 )
)
16. Что такое скалярное произведение двух векторов(скалярным произведением двух векторов называется произведение их длин на косинус угла между ними -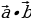 =
= 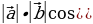 )).
)).
17. В каком случае скалярное произведение ненулевых векторов: а) равно0 - тогда и только тогда, когда эти векторы перпендикулярны. б) больше 0 - тогда и только тогда, когда угол между векторами меньше 90 в) меньше 0 -тогда и только тогда, когда угол между векторами больше 90
в) меньше 0 -тогда и только тогда, когда угол между векторами больше 90 .
.
18. Выведите формулу , выражающую скалярное произведение векторов через их координаты ( в прямоугольной системе координат скалярное произведение векторов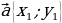 и
и 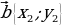 выражается формулой
выражается формулой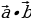 =
= 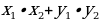 )
)
19. Запишите условие перпендикулярности двух ненулевых векторов с координатами 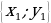 и
и 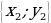 (ненулевые векторы перпендикулярны тогда и только тогда , когда
(ненулевые векторы перпендикулярны тогда и только тогда , когда 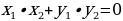 .)
.)
20 . Выведите формулу, выражающую косинус угла между ненулевыми векторами через из координаты (косинус угла 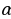 между ненулевыми векторами
между ненулевыми векторами 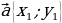 и
и 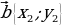 выражается формулой
выражается формулой cos
cos 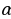 =
=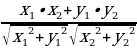 ), или cos
), или cos 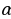 =
=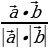 )
)
21. Сформулируйте и докажите утверждения о свойствах скалярного произведения векторов ( для любых векторов
( для любых векторов  ,
, 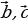 и любого числа k справедливы соотношения:
и любого числа k справедливы соотношения:
1.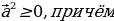
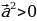 при
при 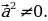
2. 
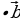 =
=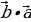 - переместительный закон
- переместительный закон
3. (  +
+ )
) 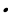 c ⃗ =
c ⃗ = 
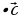 +
+ 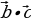 – распределительный закон
– распределительный закон
4.( k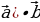 =k (
=k (
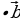 ) – сочетательный закон ).
) – сочетательный закон ).

9 класс Тема 5 Длина окружности и площадь круга. Геометрия
1.Какой многоугольник называется правильным? Приведите примеры правильных многоугольников
( правильным многоугольником называется выпуклый многоугольник, у которого все углы равны и все стороны равны.)
2.Выведите формулу для вычисления угла правильного n-угольника. (  =
=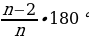 )
)
3.Сформулируйте и докажите теорему об окружности , описанной около правильного
многоугольника. (около любого правильного многоугольника можно описать окружность, и притом только одну)
4. Сформулируйте и докажите теорему об окружности , вписанной в правильный
многоугольник.(в любой правильный многоугольник можно вписать окружность , и притом только одну. Следствие1.окружность, вписанная в правильный многоугольник, касается сторон многоугольника в их серединах.
Следствие 2. Центр окружности, описанной около правильного многоугольника, совпадает с центром окружности, вписанной в тот же многоугольник . )
5.Выведите формулу для вычисления площади правильного многоугольника через его периметр и радиус вписанной окружности. ( 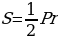 )
)
6. Выведите формулу для вычисления стороны правильного n-угольника и радиуса вписанной в него окружность через радиус описанной окружности. (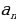 =2RSin
=2RSin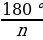 ; r =R Cos
; r =R Cos 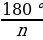 ).
).
7.Как выражаются стороны правильного треугольника , квадрата и правильного шестиугольника через радиус описанной окружности? ( =2R sin60
=2R sin60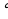 =2R
=2R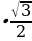 =R
=R ;
; 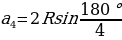 =2R sin45
=2R sin45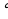 =2R
=2R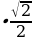 =R
=R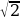 ;
; 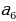 =
= =2R sin30
=2R sin30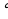 =2R
=2R =R; )
=R; )
8.Выведите формулу для вычисления длины окружности. )
)
9.Объяснити , какое число обозначается буквой 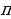 и чему равно его приближённое значение. (
и чему равно его приближённое значение. ( 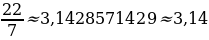 )
)
10. Выведите формулу для вычисления длины дуги окружности.(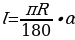 )
)
11. Выведите формулу для вычисления площади круга( S =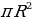 ).
).
12.Что такое круговой сектор? Выведите формулу для вычисления площади кругового сектора. (Круговым сектором или просто сектором называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга). Дуга, которая ограничивает сектор, называется дугой сектора. 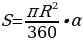 .
.
13.Что такое круговой сегмент? Объясните, как можно вычислить его площадь. (Круговым сегментом или просто сегментом называется часть круга, ограниченная дугой окружности и хордой, соединяющей концы этой дуги . Если градусная мера дуги меньше 180 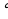 , то площадь сегмента можно найти, вычитая из площади сектора площадь равнобедренного треугольника, сторонами которого являются два радиуса и хорда сегмента.)
, то площадь сегмента можно найти, вычитая из площади сектора площадь равнобедренного треугольника, сторонами которого являются два радиуса и хорда сегмента.)
9 класс Тема 6 Движения. Геометрия
1. Объясните, что такое отображение плоскости на себя. ( Каждой точке плоскости сопоставляется ( ставится в соответствие) какая- то точка этой же плоскости, причём любая точка плоскости оказывается сопоставленной некоторой точке)
2.Какое отображение плоскости называется : а) осевой симметрией; б) центральной симметрией?
а)( осевая симметрия – это отображение плоскости на себя, которое сохраняет расстояние между точками)б) (центра́льной симметри́ей относительно точки О, называют преобразование плоскости переводящее точку X в такую точку X′, что О — середина отрезка XX′.)
3.Докажите , что осевая симметрия является отображением плоскости на себя. ( с. 287)
4.Что такое движение ( перемещение) плоскости? (движение плоскости - это отображение плоскости на себя , сохраняющее расстояние)
5.Докажите, что осевая симметрия является движением (с.288)
6. Является ли центральная симметрия движением? (центральная симметрия плоскости также является движением)
7.Докажите, что при движении отрезок отображается на отрезок. ( с. 289)
8. Докажите, что при движении треугольник отображается на равный ему треугольник. ( с.290)
9. Объясните, что такое наложение.( наложение - это отображение плоскости на себя)
10.Докажите, что при наложении различные точки отображаются в различные точки.( с. 291)
11. Докажите, что наложение является движением плоскости.( с.291)
12. Докажите, что любое движение является наложением. ( с. 292)
13.Верно ли утверждение, что при движении любая фигура отображается на равную ей фигуру?( да )
14.Какое отображение плоскости называется параллельным переносом на данный вектор? (параллельным переносом на вектор называется отображение плоскости на себя, при котором каждая точка М отображается в такую точку
называется отображение плоскости на себя, при котором каждая точка М отображается в такую точку 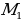 , что вектор
, что вектор 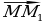 равен вектору
равен вектору  )
)
15. Докажите, что параллельный перенос является движением ( с.294)
16. Какое отображение плоскости называется поворотом? ( поворотом плоскости вокруг точки О на угол 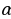 называется отображение плоскости на себя, при котором каждая точка М отображается в такую точку
называется отображение плоскости на себя, при котором каждая точка М отображается в такую точку 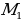 , что ОМ = О
, что ОМ = О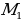 и угол МО
и угол МО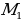 равен
равен 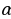 )
)
17. Докажите, что поворот является движением. ( с.295)

9 класс Тема 7 Начальные сведения из стереометрии. Геометрия
Об аксиомах планиметрии
1.Объясните, что такое многогранник; что такое грани, рёбра, вершины и диагонали многогранника. Приведите примеры многогранников.(с.300-303)
2. Объясните, как построить многогранник, называемый n-угольной призмой; что такое основания, боковые грани, боковые рёбра и высота призмы.(с.303)
3. Какая призма называется : а) прямой ; б) правильной?( а) если все боковые рёбра призмы перпендикулярны к плоскостям её оснований , то призма называется прямой. б)прямая призма , основаниями которой являются правильные многоугольники, называется правильной.)
4. Объясните, что такое параллелепипед; какие многоугольники являются гранями: а) параллелепипеда; б)прямого параллелепипеда; в) прямоугольного параллелепипеда. ( четырёхугольная призма, основаниями которой являются параллелограммы, называется параллелепипедом. а)параллелограммы; б)прямоугольники; в)прямоугольники.
5. Докажите, что четыре диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.(с,305)
6. Объясните, как измеряются объёмы тел; что показывает число. выражающее объём тела при выбранной единице измерения объёмов( с, 306-307)
7.Сформулируйте основное свойство объёмов.( 1. Равные тела имеют равные объёмы; 2.(Если тело составлено из нескольких тел, то его объём равен сумме объёмов этих тел).
8. Объясните, в чём заключается принцип Кавальери. (С.307-308)
9.Что такое измерения прямоугольного параллелепипеда? Докажите, что квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.( длина, ширина и высота; с.309)
10. Докажите, что объём прямоугольного параллелепипеда равен произведению трёх его измерений. ( с.309-310) V = abc
11. Какой формулой выражается объём призмы? (объём призмы равен произведению площади основания на высоту) 
12. Объясните, как построить многогранник, называемый n-угольной пирамидой; что такое основания, боковые грани, вершина, боковые рёбра и высота пирамиды.( c.311-312)
13. Объясните, какая пирамида называется правильной; что такое апофема правильной пирамиды. ( пирамида называется правильной , если её основание –правильный многоугольник, высота боковой грани правильной пирамиды , проведённая из её вершины, называется апофемой)
14. Какой формулой выражается объём пирамиды?( объём пирамиды равен одной трети произведения площади основания на высоту)
15. Объясните, какое тело называется цилиндром; что такое ось, высота, основания, радиус, боковая поверхность, образующие цилиндра? (с. 319) ( цилиндр – это тело, ограниченное двумя равными кругами и цилиндрической поверхностью)
16. Какой формулой выражается объём цилиндра?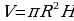
17. Объясните, как получается и что представляет собой развёртка боковой поверхности цилиндра? ( с.319-320)
18 Какой формулой выражается площадь боковой поверхности цилиндра? -площадь боковой поверхности цилиндра равна площади её развёртки.)
-площадь боковой поверхности цилиндра равна площади её развёртки.)
19. Объясните. какое тело называется конусом; что такое ось, высота, основания, боковая поверхность, образующие конуса. (конус - это тело , ограниченное кругом и конической поверхностью) с.320-321
20. Какой формулой выражается объём конуса? ( площадь конуса равен одной трети произведения площади основания на высоту) 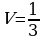
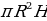
21. Объясните, как получается и что представляет собой развёртка боковой поверхности конуса?(с.321)
22. Какой формулой выражается площадь боковой поверхности конуса? (площадь боковой поверхности конуса с образующей 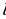 и радиусом основания r выражается формулой :
и радиусом основания r выражается формулой :  )
)
23.Что называется сферой и что такое её центр, радиус и диаметр?( сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки, данная точка называется центром сферы , данное расстояние - радиусом сферы. Отрезок , соединяющий две точки сферы и проходящий через её центр, называется диаметром сферы)
24.Какое тело называется шаром и что такое его центр, радиус и диаметр? ( тело , ограниченное сферой , называется шаром , -центр , радиус и диаметр сферы называется также центром, радиусом и диаметром шара)
25. Какой формулой выражается объём шара? 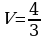
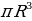
26 . Какой формулой выражается площадь сферы? S =4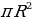







 и
и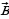 коллинеарны и
коллинеарны и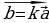 )
)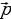 = х
= х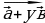 , где х и у некоторые числа , то говорят , что вектор
, где х и у некоторые числа , то говорят , что вектор 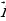 и
и  называются координатными векторами)
называются координатными векторами)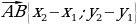
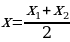
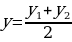 .
.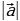 =
=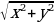 ).
).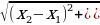 ).
). ) имеет вид:
) имеет вид:  =
=
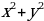 =
= 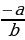 , d =
, d =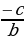 . Число k называется угловым коэффициентом прямой)
. Число k называется угловым коэффициентом прямой) R , то окружности называются концентрическими, и окружность радиуса r лежит внутри круга радиуса R .
R , то окружности называются концентрическими, и окружность радиуса r лежит внутри круга радиуса R . – одна окружность лежит внутри другой 3.
– одна окружность лежит внутри другой 3.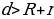 – одна окружность лежит вне другой 4.
– одна окружность лежит вне другой 4.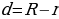 – окружности касаются изнутри 5.
– окружности касаются изнутри 5.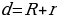 - окружности касаются извне 6.
- окружности касаются извне 6.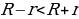 – окружности пересекаются в двух точках
– окружности пересекаются в двух точках 0).
0).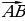 называется длина отрезка АВ . длина вектора
называется длина отрезка АВ . длина вектора  ) обозначается так:
) обозначается так: 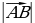 (
(
 и противоположно направленные векторы
и противоположно направленные векторы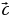 и
и 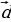 . (
. (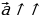
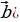 - обозначение сонаправленных векторов, (
- обозначение сонаправленных векторов, ( ) - противоположно направленные вектора
) - противоположно направленные вектора Правило треугольника можно сформулировать следующим образом: если А, В и С – произвольные точки , то
Правило треугольника можно сформулировать следующим образом: если А, В и С – произвольные точки , то 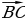 =
= 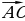 )
)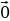 =
= – сочетательный закон.
– сочетательный закон.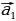 называется противоположный вектору
называется противоположный вектору 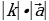 причём векторы
причём векторы 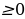 и противоположно направлены при k
и противоположно направлены при k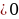 . Произведение нулевого вектора на любое число считается нулевой вектор).
. Произведение нулевого вектора на любое число считается нулевой вектор).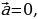 k = 0 (произведение любого вектора на число нуль есть нулевой вектор)
k = 0 (произведение любого вектора на число нуль есть нулевой вектор)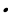
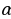 из промежутка
из промежутка 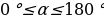 (для любого угла
(для любого угла 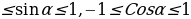 )
) 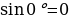 ,
, 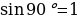 .
. 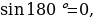
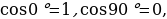
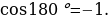
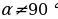 ) называется отношение
) называется отношение 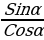 , т.е.
, т.е. 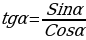 . При
. При 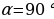
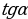 не определён , поскольку
не определён , поскольку 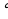 Cos 90 =0 и в формуле знаменатель обращается в нуль. Используя формулы , находим:
Cos 90 =0 и в формуле знаменатель обращается в нуль. Используя формулы , находим: 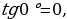
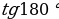 = 0 ).
= 0 ). 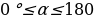 ) называется отношение
) называется отношение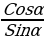 , т.е.
, т.е.  . При
. При 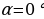 и
и 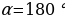
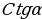 не определён. Исходя из формул
не определён. Исходя из формул 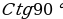 = 0).
= 0). 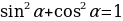 )
)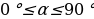
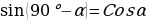 , Cos (
, Cos (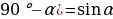 .
.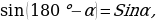

 .Сформулируйте и докажите теорему о площади треугольника( вычисление площади треугольника по двум сторонам и углу между ними)-
.Сформулируйте и докажите теорему о площади треугольника( вычисление площади треугольника по двум сторонам и углу между ними)-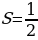 absin C
absin C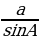 =
=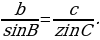 Замечание к теореме синусов (
Замечание к теореме синусов (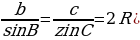
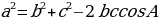
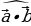
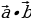 =
= 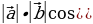 )).
)).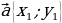 и
и 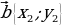 выражается формулой
выражается формулой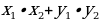 )
)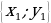 и
и 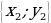 (ненулевые векторы перпендикулярны тогда и только тогда , когда
(ненулевые векторы перпендикулярны тогда и только тогда , когда 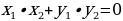 .)
.) cos
cos 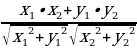 ), или cos
), или cos 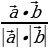 )
)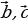 и любого числа k справедливы соотношения:
и любого числа k справедливы соотношения: 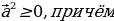
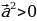 при
при 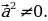
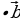 =
=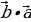 - переместительный закон
- переместительный закон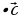 +
+ 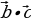 – распределительный закон
– распределительный закон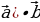 =k (
=k ( =
=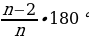 )
)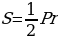 )
)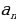 =2RSin
=2RSin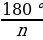 ; r =R Cos
; r =R Cos  =2R sin60
=2R sin60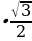 =R
=R ;
; 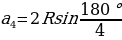 =2R sin45
=2R sin45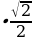 =R
=R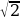 ;
; 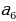 =
= =2R sin30
=2R sin30 =R; )
=R; ) 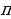 и чему равно его приближённое значение. (
и чему равно его приближённое значение. ( 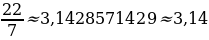 )
)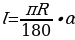 )
)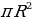 ).
).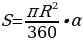 .
.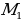 , что вектор
, что вектор 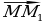 равен вектору
равен вектору 

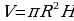
 -площадь боковой поверхности цилиндра равна площади её развёртки.)
-площадь боковой поверхности цилиндра равна площади её развёртки.)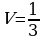
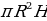
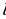 и радиусом основания r выражается формулой :
и радиусом основания r выражается формулой :