Тема. Лабораторная работа «Определение индукции магнитного поля Земли.»
Цель.
-
Учебная. Ввести понятие электромагнитной индукции. Записать формулы самоиндукции и индуктивности .
-
Развивающая. Развивать логическое мышление и естественно - научное мировоззрение у студентов.
-
Воспитательная. Воспитывать интерес к явлениям природы, научным достижениям и открытиям. Воспитывать навыки при выполнении лабораторных работ.
Межпредметные связи:
-
Обеспечивающие: математика(расчет формул).
-
Обеспечиваемые: математика, информатика( программа «Физика в картинках»).
Методическое обеспечение и оборудование:
-
Методическая разработка к занятию.
-
Учебная программа
-
Рабочая программа.
-
Инструктаж по технике безопасности.
-
Кадоскопные карты « Электромагнитная индукция».
-
Карточки с дифференцированными вопросами и задачами
-
Диафильм «Электромагнитная индукция».
Технические средства обучения: кодоскоп, диапроектор.
Обеспечение рабочих мест:
Ход занятия.
Организационный момент.
Анализ и проверка домашней работы.
-
Что называется силой Лоренца?
-
Сформулируйте правило левой руки.
-
Как движется частица в магнитном поле?
-
Что такое ускоряющая разность потенциалов?
-
Какие виды циклических ускорителей вы знаете?
-
В чем заключается эффект Холла?
-
Что такое удельный заряд частицы?
Мотивация.
В 1831 г. М. Фарадеем экспериментально было обнаружено, что в замкнутом контуре возникает электрический ток при изменении маг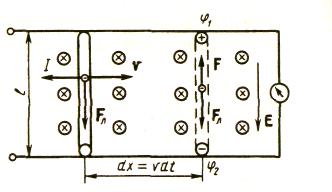 нитного потока, пронизывающего его. Это явление было названо электромагнитной индукцией (индукция — значит наведение).
нитного потока, пронизывающего его. Это явление было названо электромагнитной индукцией (индукция — значит наведение).
Проводя многочисленные опыты, Фарадей установил, что в замкнутых проводящих контурах возникает электрический ток при всяком изменении магнитного потока, пронизывающего
контур, независимо от того, каким способом достигается изменение потока индукции магнитного поля во времени.
Электромагнитная индукция
Ток, возникающий при электромагнитной индукции, называют индукционным.
Рассмотрим возникновение ЭДС индукции, а следовательно, и индукционного тока. Пусть проводник без тока длиной / движется в магнитном поле со скоростью и. Магнитное поле однородно. Вектор магнитной индукции направлен перпендикулярно плоскости от нас (рис.). При движении проводника вправо свободные электроны, содержащиеся в нем, будут двигаться также вправо, т. е. возникает конвекционный ток. Направление этого тока противоположно направлению движения электронов. На каждый движущийся электрон со стороны магнитного поля действует сила Лоренца. Заряд электрона отрицательный, поэтому сила Лоренца Fл направлена вниз. Следовательно, электроны под действием этой силы движутся вниз и в нижней части проводника длиной l будут накапливаться отрицательные заряды, а в верхней — положительные. В результате этого образуется разность потенциалов 1-2 таким образом, в проводнике возникает электрическое поле напряженностью Е, которое препятствует дальнейшему перемещению электронов.
Заряды перестанут перемещаться при такой напряженности Е электрического поля, когда сила еЕ, действующая со стороны электрического поля, будет равна по модулю, но противоположна по направлению силе evB, действующей со стороны магнитного поля:
eE = -evB или E = -vB.
Напряженность Е электрического поля в движущемся проводнике длиной l и разность потенциалов 1-2 связаны между собой соотношением
1-2 = El или 1-2 = -VВ1.
Если такой проводник замкнуть, то по цепи пойдет ток. Таким образом, на концах проводника длиной l, движущегося со скоростью v в однородном магнитном поле В, индуцируется ЭДС Eинд = -vBL
Учитывая, что v = dx/dt , преобразуем формулу: 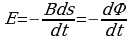
[ldx - dS —площадь контура, «сметаемого» проводником длиной l при движении за промежуток времени dt].
ЭДС индукции в контуре равна скорости изменения магнитного потока сквозь поверхность, ограниченную контуром (закон электромагнитной индукции, или закон Фарадея).
Используя закон Ома для полной цепи и закон Фарадея, получаем выражение для индукционного тока:
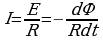
Из уравнения следует, что индукционный ток зависит от сопротивления контура.
Направление индукционного тока определяется по правилу Ленца.
Индукционный ток всегда направлен так, что его действие противоположно действию причины, вызывающей ток (правило Ленца).
Электродвижущая сила в цепи — это результат действия сторонних сил, т. е. сил неэлектрического происхождения. При движении проводника в магнитном поле роль сторонних сил выполняет сила Лоренца, под действием которой происходит разделение зарядов, в результате чего на концах проводника появляется разность потенциалов. ЭДС индукции в проводнике является работой по перемещению единичного положительного заряда вдоль проводника.
Таким образом, переменное магнитное поле вызывает появление индуцированного электрического поля. Это поле является непотенциальным, так как работа, совершаемая в этом поле при перемещении единичного положительного заряда по замкнутой цепи, равна ЭДС индукции, а не нулю. Такие поля называют вихревыми. Силовые линии вихревого электрического поля замкнуты сами на себя в отличие от линий напряженности электростатического поля.
Если замкнутый контур содержит N последовательно соединенных витков (например, катушка или соленоид), то ЭДС индукции равна сумме ЭДС каждого витка:
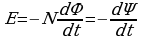
[d = N dФ — потокосцепление, т. е. суммарный магнитный поток сквозь N витков].
Самоиндукция. Индуктивность контура
ЭДС электромагнитной индукции, которая возникает в контуре при изменении силы тока в нем, называется ЭДС самоиндукции. Это частный случай электромагнитной индукции.
ЭДС самоиндукции определяется из закона Фарадея: 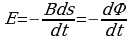
Магнитный поток, сцепленный с контуром, всегда пропорционален силе тока в нем: Ф=LI
Коэффициент пропорциональности L называют коэффициентом самоиндукции (индуктивностью контура).
Единица индуктивности — генри (Гн).
Индуктивность — одна из основных характеристик цепи переменного тока. Подставляя в формулу выражение, получаем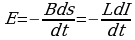
Если контур представляет собой соленоид, содержащий N витков, то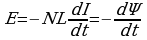
[d —потокосцепление].
В результате самоиндукции при замыкании цепи сила тока в соленоиде никогда сразу не достигает максимального значения, а нарастает постепенно. При размыкании цепи возникает индукционный ток, идущий в том же направлении, что и основной, и проявляющийся в виде искры на контактах рубильника.
Индуктивность L зависит от формы и размеров соленоида, а также от магнитных свойств окружающей среды. Если размеры, форма соленоида и магнитные свойства окружающей среды не изменяются, то
L = const.
Определим индуктивность соленоида, т. е. катушки, длина l которой много больше ее диаметра. В этом случае можно пренебречь искажением поля вблизи концов соленоида. Напряженность поля во всех точках внутри соленоида одинакова и равна Я = In, где я — число витков, приходящихся на единицу длины соленоида. Если общее число витков соленоида N равно N, то Н = In. Магнитный поток, пронизывающий один виток
соленоида, равен Ф= BS=0INS/l
[S — площадь поперечного сечения соленоида; — относительная магнитная проницаемость окружающей среды].
Полный магнитный поток равен потокосцеплению: =NФ=0N2IS/l. Так как Sl = V (объем соленоида), то
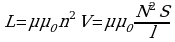
Взаимная индукция
Взаимной индукцией называют возникновение ЭДС индукции в одном из контуров (1) при изменении силы тока в другом (2), находящемся вблизи него (рис.).
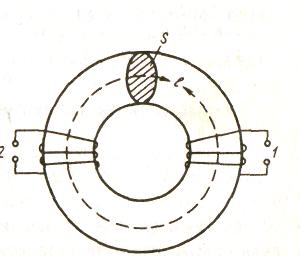 Явление взаимной индукции рассмотрим на примере трансформатора. Если на общий сердечник намотаны две катушки, то изменение силы тока в одной из них (1) будет индуцировать в другой катушке (2) ЭДС, которую можно определить по закону Фарадея. Если по первой катушке пропустить ток I то он создаст магнитное поле, магнитный поток которого пронижет катушку 2. Очевидно, что поток Ф 2, пронизывающий катушку 2, зависит от индукции магнитного поля в тех местах, где она находится. Индукция магнитного поля зависит от силы тока I, протекающего по катушке 1, формы, размеров и взаимного расположения катушек, а также магнитных свойств окружающей среды. Эту зависимость учитывает коэффициент М21, называемый взаимной индуктивностью. Тогда Ф2 = М21I1.
Явление взаимной индукции рассмотрим на примере трансформатора. Если на общий сердечник намотаны две катушки, то изменение силы тока в одной из них (1) будет индуцировать в другой катушке (2) ЭДС, которую можно определить по закону Фарадея. Если по первой катушке пропустить ток I то он создаст магнитное поле, магнитный поток которого пронижет катушку 2. Очевидно, что поток Ф 2, пронизывающий катушку 2, зависит от индукции магнитного поля в тех местах, где она находится. Индукция магнитного поля зависит от силы тока I, протекающего по катушке 1, формы, размеров и взаимного расположения катушек, а также магнитных свойств окружающей среды. Эту зависимость учитывает коэффициент М21, называемый взаимной индуктивностью. Тогда Ф2 = М21I1.
По закону электромагнитной индукции Фарадея, ЭДС, возбуждаемая в катушке 2 переменным магнитным полем катушки 1, равна 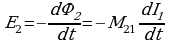
Проводя аналогичные рассуждения Для катушки 2, получаем, что магнитный поток Ф, и электродвижущая сила E1 вызываемая в первом контуре переменным током I2 второго контура, равны
Ф,=M12I2, 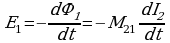
[коэффициенты М21 – М12 = М являются характеристикой двух контуров].
В большинстве трансформаторов первичная и вторичная обмотки наматываются одна поверх другой так, что магнитный поток, пронизывающий их, одинаков, т. е. отношение dФ/dt одинаково для обеих обмоток. Если число витков первичной катушки N1 а вторичной -N2, то в первичной и вторичной катушках индуцируются
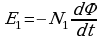
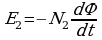 Отношение этих ЭДС равно
Отношение этих ЭДС равно 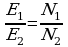 .
.
Таким образом, система из двух катушек, соединенных ферромагнитным сердечником, представляет собой трансформатор, с помощью которого можно повышать или понижать напряжение переменного тока в зависимости от числа витков первичной и вторичной обмоток.
Энергия магнитного поля
Если в контуре с индуктивностью L течет ток I, то в момент размыкания цепи возникает индукционный ток и им совершается работа. Эта работа совершается за счет энергии исчезнувшего при размыкании цепи магнитного поля. На основании закона сохранения и превращения энергии энергия магнитного поля превращается главным образом в энергию электрического поля, за счет которой происходит нагревание проводников. Работа может быть определена из соотношения d А =EcIdt.
Так как 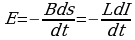
dA=-LIdI. Уменьшение энергии магнитного поля равно работе тока, поэтому 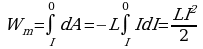
Формула справедлива для любого контура и показывает, что энергия магнитного поля зависит от индуктивности контура и силы тока, протекающего по нему.
Рассчитаем энергию однородного магнитного поля длинного соленоида, индуктивность которого определяется по формуле 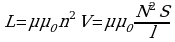 . В этом случае формула примет вид
. В этом случае формула примет вид 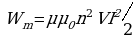
Учитывая, что напряженность поля внутри бесконечно длинного соленоида Н=In, получаем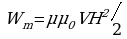
Выразим энергию через индукцию магнитного поля В = 0Н:
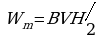
Вследствие того что магнитное поле соленоида однородно и локализовано внутри соленоида, энергия распределена по объему соленоида с постоянной плотностью =W\V получаем 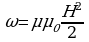
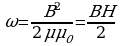
Так, для электрического поля величина 1/С, обратная емкости, аналогична упругости пружины, а для магнитного поля индуктивность L аналогична массе m тела. Таким образом, индуктивность является мерой «инертности» контура по отношению к изменению в нем тока.
Токи при замыкании и размыкании цепи
При определении силы тока в контуре по формуле предполагалось, что в нем действует лишь ЭДС, равная 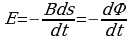 . В общем случае в контуре могут действовать и другие источники тока, например аккумулятор батареи E. Тогда
. В общем случае в контуре могут действовать и другие источники тока, например аккумулятор батареи E. Тогда 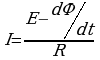 [R — полное сопротивление контура].
[R — полное сопротивление контура].
Рассмотрим случаи замыкания и размыкания цепи. Согласно выражению 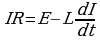
откуда 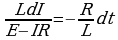 . Умножим обе части этого выражения на (-R/L):
. Умножим обе части этого выражения на (-R/L):
Проинтегрируем полученное выражение: 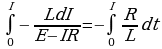
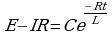
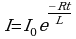
Следовательно, сила тока в контуре изменяется не мгновенно, а по экспоненциальному закону.
Из формул следует, что чем больше R\L, тем быстрее завершается переходный процесс при замыкании и размыкании цепи.
ИНСТРУКЦИЯ К ВЫПОЛНЕНИЮ
ЛАБОРАТОРНОЙ РАБОТЫ ПО ФИЗИКЕ
ОПРЕДЕЛЕНИЕ ИНДУКЦИИ МАГНИТНОГО ПОЛЯ ЗЕМЛИ БАЛЛИСТИЧЕСКИМ МЕТОДОМ
ЦЕЛЬ. Научиться определять магнитное поле Земли в любом месте наблюдения.
Оборудование: проволочная катушка; гальванометр типа М-273/9;
компас (магнитная стрелка); омметр.
Метод выполнения работы
Для измерения индукции магнитного поля Земли можно применить следующий способ. Представим себе плоский контур площадью S, расположенный в пространстве
таким образом, что вектор В индукции магнитного поля Земли перпендикулярен
плоскости контура. Магнитный поток Ф через контур в этом случае
равен произведению модуля вектора индукции В магнитного поля Земли на
площадь S контура:
Ф = BS.
При повороте контура в пространстве на 180° магнитный поток Ф через контур,
оставаясь тем же по модулю, изменяет свой знак. Изменение магнитного потока
через контур при его повороте равно:
 Ф = Ф-(-Ф) = 2ВS.
Ф = Ф-(-Ф) = 2ВS.
Изменение магнитного потока через контур сопровождается возникновением ЭДС
индукции, равной по закону электромагнитной индукции

В катушке из п витков провода ЭДС индукции в п раз больше:
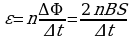
Если выводы катушки на рамке закоротить, в цепи будет протекать индукционный ток
I=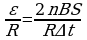 ' Умножив обе части уравнения на
' Умножив обе части уравнения на  , получим:
, получим:
i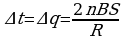 Из последнего уравнения следует:
Из последнего уравнения следует:
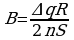
где 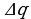 — заряд, протекающий в цепи при повороте рамки, R — общее электрическое
— заряд, протекающий в цепи при повороте рамки, R — общее электрическое
сопротивление цепи, складывающееся из сопротивлений катушки и рамки
гальванометра.
Заряд 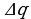 можно измерить с помощью гальванометра, подключенного
можно измерить с помощью гальванометра, подключенного
к концам катушки на рамке, если его предварительно отградуировать. Градуировка
шкалы гальванометра в единицах заряда осуществляется путем подключения его
к обкладкам конденсатора известной емкости, заряженного до известного напряжения.
При практическом выполнении работы, когда расположение вектора В
индукции магнитного поля в пространстве неизвестно, можно в двух
отдельных опытах определить горизонтальную Вт и вертикальную В3 компоненты
вектора В и вычислить модуль В их геометрической суммы:
в=вг+вв, B=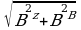
Порядок выполнения работы
Изготовьте рамку размером примерно 50Х 50 см и намотайте
на нее 50—100 витков медного провода.
1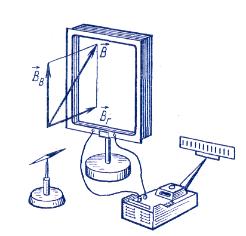 . Присоедините выводы катушки на рамке к гальванометру.
. Присоедините выводы катушки на рамке к гальванометру.
Установите рамку вертикально и расположите ее плоскость перпендикулярно горизонтальной составляющей вектора индукции магнитного поля Земли, ориентируясь по стрелке компаса (рис. 1).
Поверните рамку на 180° вокруг вертикальной оси и сделайте отсчет заряда 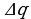 по отбросу стрелки гальванометра.
по отбросу стрелки гальванометра.
2.Повторите опыт 5 раз и найдите среднее значение количества электричества 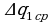 протекающего через гальванометр при повороте рамки на 180°.
протекающего через гальванометр при повороте рамки на 180°.
Измерьте площадь рамки S.
По измеренным значениям 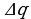 1ср и S и известному значению числа витков провода на рамке п\ вычислите модуль Вг горизонтальной составляющей вектора индукции магнитного поля Земли.
1ср и S и известному значению числа витков провода на рамке п\ вычислите модуль Вг горизонтальной составляющей вектора индукции магнитного поля Земли.
3. Расположите рамку горизонтально и поверните ее на 180° вокруг горизонтальной оси. Сделайте отсчет заряда q2. Повторите опыт 5 раз и найдите среднее значение 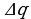 2ср. Рассчитайте модуль Ве вертикальной составляющей вектора индукции магнитного поля
2ср. Рассчитайте модуль Ве вертикальной составляющей вектора индукции магнитного поля
Земли.
4. Вычислите модуль В индукции магнитного поля Земли. Результаты измерений и вычислений занесите в отчетную таблицу.
Отчетная таблица
| R, Ом | N1 | S,м2 |  q1, Кл q1, Кл
| Bz,Тл | N2 |  qср, Кл qср, Кл
| Bв,Тл | Bср, Тл |
| 2 | 50 |
| 2нКЛ |
| 10 | 10нКл |
|
|
| 4 | 100 |
| 4нКл |
| 20 | 12нКл |
|
|
| 6 | 150 |
| 6нКл |
| 30 | 14нКл |
|
|
| 8 | 200 |
| 8нКл |
| 40 | !6нКл |
|
|
КОНТРОЛЬНЫЕ ВОПРОСЫ.
-
В чем состоит сущность баллистического метода измерения магнитной индукции?
-
Сформулируйте закон электромагнитной индукции.
-
Что называется магнитным потоком?
Домашнее задание: отчет о лабораторной работе.
Литература:
-
Физика. Учебник для средних специальных учебных заведений, Жданов Л.С. В. школа 1983г.
-
Сборник задач и вопросов по физике. Гладковой Р. А.-М. 1988г.
-
Физика,10-11 классы. Гончаренко С. У. Образование 1996 г.
-
Савельев Курс общей физики М. Просвещение 1988 г.





 нитного потока, пронизывающего его. Это явление было названо электромагнитной индукцией (индукция — значит наведение).
нитного потока, пронизывающего его. Это явление было названо электромагнитной индукцией (индукция — значит наведение).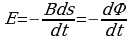
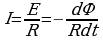
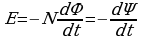
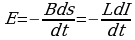
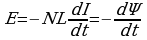
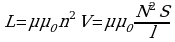
 Явление взаимной индукции рассмотрим на примере трансформатора. Если на общий сердечник намотаны две катушки, то изменение силы тока в одной из них (1) будет индуцировать в другой катушке (2) ЭДС, которую можно определить по закону Фарадея. Если по первой катушке пропустить ток I то он создаст магнитное поле, магнитный поток которого пронижет катушку 2. Очевидно, что поток Ф 2, пронизывающий катушку 2, зависит от индукции магнитного поля в тех местах, где она находится. Индукция магнитного поля зависит от силы тока I, протекающего по катушке 1, формы, размеров и взаимного расположения катушек, а также магнитных свойств окружающей среды. Эту зависимость учитывает коэффициент М21, называемый взаимной индуктивностью. Тогда Ф2 = М21I1.
Явление взаимной индукции рассмотрим на примере трансформатора. Если на общий сердечник намотаны две катушки, то изменение силы тока в одной из них (1) будет индуцировать в другой катушке (2) ЭДС, которую можно определить по закону Фарадея. Если по первой катушке пропустить ток I то он создаст магнитное поле, магнитный поток которого пронижет катушку 2. Очевидно, что поток Ф 2, пронизывающий катушку 2, зависит от индукции магнитного поля в тех местах, где она находится. Индукция магнитного поля зависит от силы тока I, протекающего по катушке 1, формы, размеров и взаимного расположения катушек, а также магнитных свойств окружающей среды. Эту зависимость учитывает коэффициент М21, называемый взаимной индуктивностью. Тогда Ф2 = М21I1. 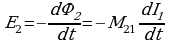
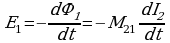
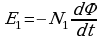
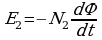 Отношение этих ЭДС равно
Отношение этих ЭДС равно 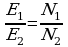 .
.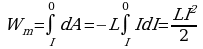
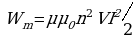
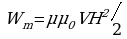
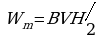
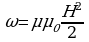
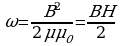
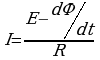 [R — полное сопротивление контура].
[R — полное сопротивление контура].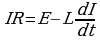
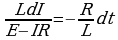 . Умножим обе части этого выражения на (-R/L):
. Умножим обе части этого выражения на (-R/L): 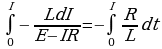
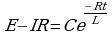
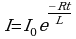
 Ф = Ф-(-Ф) = 2ВS.
Ф = Ф-(-Ф) = 2ВS.
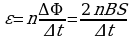
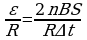 ' Умножив обе части уравнения на
' Умножив обе части уравнения на  , получим:
, получим: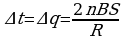 Из последнего уравнения следует:
Из последнего уравнения следует: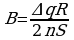
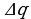 — заряд, протекающий в цепи при повороте рамки, R — общее электрическое
— заряд, протекающий в цепи при повороте рамки, R — общее электрическое 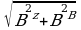
 . Присоедините выводы катушки на рамке к гальванометру.
. Присоедините выводы катушки на рамке к гальванометру.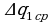 протекающего через гальванометр при повороте рамки на 180°.
протекающего через гальванометр при повороте рамки на 180°.



















