Лекция- мастер класс.
Тема. Действие магнитного поля на движущийся заряд. Сила Лоренца Эффект Холла.
Цель.
-
Учебная. Вывести формулы расчета движения заряженной частицы в магнитном поле. Рассказать об эффекте Холла.
-
Развивающая. Развивать логическое мышление и естественное - научное мировоззрение.
-
Воспитательная. Воспитывать интерес к явлениям природы, научным достижениям и открытиям.
-
Дидактическая: мастер-класс для преподавателей естественно-математических дисциплин.
Межпредметные связи:
-
Обеспечивающие: химия, математика, информатика,.
-
Обеспечиваемые: химия, математика, информатика.
Методическое обеспечение и оборудование:
-
Методическая разработка к занятию.
-
Учебный план.
-
Учебная программа
-
Рабочая программа.
-
Инструктаж по технике безопасности.
-
Карточки с дифференцированными вопросами.
Технические средства обучения: монитор компьютера. DVD, фильм студии « Кварт». Магнетизм, часть 2.
Обеспечение рабочих мест:
Ход лекции.
-
Организационный момент.
-
Анализ и проверка домашней работы
Действие магнитного поля на движущийся заряд. Сила Лоренца
Движущиеся электрические заряды создают вокруг себя магнитное поле, которое распространяется в вакууме со скоростью света. При движении заряда во внешнем магнитном поле возникает силовое взаимодействие магнитных полей, определяемое по закону Ампера. Процесс взаимодействия магнитных полей исследовался Лоренцем, который вывел формулу для расчета силы, действующей со стороны магнитного поля на движущуюся заряженную частицу. Лоренц является создателем классической электронной теории. Широко известны его работы в области электродинамики, термодинамики, статической механики, оптики, теории излучения, атомной физики. За исследования влияния магнетизма на процессы излучения он в 1902 г. был удостоен Нобелевской премии.
Силу, действующую со стороны магнитного поля на движущийся заряд, можно найти исходя из закона Ампера. Пусть по проводнику длиной dl за промежуток времени dt проходит n одинаковых зарядов величиной dQ, т. е. через проводник протекает ток, сила которого I=ndQ/dt
Согласно закону Ампера, на ndQ зарядов будет действовать сила dF = BIdl sina = B
Сила, с которой поле действует на каждый заряд, равна 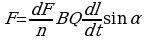
[dl/dt = v — скорость движения заряда, a — угол между вектором скорости v заряда и вектором магнитной индукции В].
Сила, действующая со стороны магнитного поля на движущийся заряд, равна
F=QvBsina и называется силой Лоренца.
Эта сила перпендикулярна векторам v и В. Направление силы Лоренца, действующей на положительный заряд, определяется по правилу левой руки С изменением знака заряда направление силы изменяется на противоположное.
Анализируя выражение, можно сделать выводы:
-
если скорость заряда v = О, то Fл = О, т. е. магнитное поле не действует на неподвижную заряженную частицу;
-
е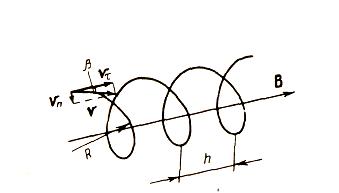 сли a = 0, sina = 0, то Рл = 0, т. е. если частица движется так, что вектор скорости v параллелен вектору магнитной индукции В, то со стороны магнитного поля сила не действует.
сли a = 0, sina = 0, то Рл = 0, т. е. если частица движется так, что вектор скорости v параллелен вектору магнитной индукции В, то со стороны магнитного поля сила не действует.
Так как сила Лоренца всегда направлена перпендикулярно вектору скорости летящей частицы, то она не изменяет величину скорости, а изменяет лишь направление движения частиц. Если заряженная частица движется в однородном магнитном поле, вектор индукции которого перпендикулярен направлению скорости заряженной частицы, то сила Лоренца искривляет траекторию движения, выполняя роль центростремительной силы. Действие этой силы не приводит к изменению энергии заряженной частицы, т. е. эта сила не совершает работы.
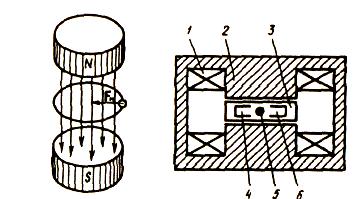
Очень важным является использование этого явления при исследовании космических частиц для определения знака заряда. Попадание летящей частицы в магнитное поле вызывает изменение ее траектории в зависимости от знака заряда (рис.). На рис.вектор индукции магнитного поля направлен перпендикулярно плоскости чертежа (от нас). Частица будет двигаться по окружности, радиус R которой можно определить из равенства центростремительной силы и силы Лоренца:
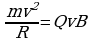
Если частица движется под углом к линиям В, то траектория движения частицы будет винтовой линией (спиралью) .
Шаг h спирали определяется гт — тангенциальной составляющей скорости v частицы. Радиус спирали зависит от и„ — нормальной составляющей скорости v.
Когда электрический заряд движется одновременно в электрическом и магнитном полях, то результирующая сила, действующая на частицу, равна
F= QvBsina+QE.
В этом случае сила имеет две составляющие: от воздействия магнитного и электрического полей. Между этими составляющими имеется принципиальная разница. Электрическое поле изменяет величину скорости, а следовательно, и кинетическую энергию частицы, однородное магнитное поле изменяет только направление ее движения.
Определение удельного заряда частицы
Совместное действие на заряженные частицы электрического и магнитного полей используется для определения удельного заряда Q/m частицы, т. е. отношения заряда Q частицы к ее массе. Для определения удельного заряда необходимо знать скорость частицы и радиус траектории в магнитном поле. Скорость частицы можно определить по ускоряющей разности потенциалов электрического поля. Работа электрических сил равна кинетической энергии частицы: 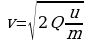
Если радиус R траектории определить экспериментально, измерить В и (ф,-ф2), то, как следует из, Таким образом был определен удельный заряд электрона е/m = = 1,7588-1011 Кл/кг и протона е/m = 9,5488-107 Кл/кг. Этим методом можно определить не только удельный заряд протона и электрона, но и иона. Зная заряд иона, можно найти его массу. Поэтому измерение Qlm для ионов является важнейшим и наиболее точным методом определения атомных масс и широко применяется в современной физике. Для этой цели существуют приборы, получившие название масс-спектрометров.
 Ускорители заряженных частиц
Ускорители заряженных частиц
Структуру атомных ядер исследуют, бомбардируя их частицами, имеющими большую энергию, т. е. летящими с большой скоростью. Для получения таких частиц в лабораторных условиях используют ускорители частиц различных видов, одним из которых является циклический ускоритель — циклотрон.
В циклотроне заряженная частица движется между полюсами электромагнита, многократно проходя сквозь электрическое поле. При этом каждый раз ее энергия возрастает на 102—103 эВ. Управление движением частицы производится с помощью поперечного магнитного поля.
На заряженную частицу, движущуюся в постоянном магнитном поле, действует сила Лоренца Fn = QvB. В результате частица движется по окружности постоянного радиуса R, если ее масса т и скорость v остаются неизменными (рис.). Сила Лоренца Fл равна силе F = mv2/R, вызывающей центростремительное ускорение:
[Q — заряд частицы, В — индукция магнитного поля (векторы v и В взаимно перпендикулярны, sin а = 1 .
И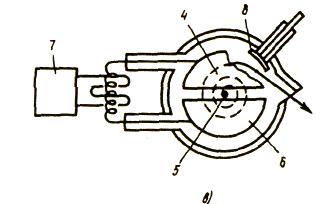 з этой формулы легко получить выражения для угловой скорости и периода вращения частицы:
з этой формулы легко получить выражения для угловой скорости и периода вращения частицы:
Если Q, m к В постоянны, то угловая скорость, а следовательно, и количество оборотов частицы в секунду тоже являются постоянными величинами, не зависящими от энергии частицы. Однако радиус траектории зависит от скорости движения частицы. С увеличением скорости движения частицы и ростом ее энергии радиус траектории увеличивается, поэтому и частица в циклотроне движется по раскручивающейся спирали.
Схема циклотрона показана на рис. 3.61, б (вид сбоку) и 3.61, в (вид сверху). Между полюсами электромагнита, состоящего из магнита 2 и обмоток 7, помещают два металлических электрода 4 и б, на которые подается высокое напряжение от высокочастотного генератора 7. Электроды называют дуантоми из-за сходства их формы с латинской буквой D. Вблизи центра магнита в промежутке между дуантами располагается источник 5 заряженных частиц (ионов). Вся система из электродов и ионного) источника помещена в вакуумную камеру 3, разрежение в которой достигает 1СГ5 мм рт. ст. Частота изменения напряженности электрического поля подбирается так, чтобы к моменту подлета иона, вылетевшего из источника 5, к зазору между дуантами там существовала ускоряющая разность потенциалов. Внутри дуантов электрическое поле отсутствует, и там ион движется по дуге постоянного радиуса, соответствующего энергии иона. В промежутках между дуантами энергия иона увеличивается, увеличивается и радиус следующего полувитка в дуанте. Ионы движутся по спирали, приближаясь к краю полюса магнита. Пучок ускоренных положительных ионов выводят из циклотрона с помощью отклоняющего электрода 8, на который подается высокий отрицательный потенциал. Проходя мимо него, пучок ионов изменяет свою траекторию и через окошко, закрытое тонкой фольгой, выходит из камеры.
Существуют различные типы циклических ускорителей:
-
циклотрон — для разгона тяжелых частиц (ионов);
-
бетатрон — для разгона электронов;
-
фазотрон — ускорители с постоянным магнитным полем и изменяемой в процессе ускорения частотой переменного электрического поля;
-
синхротрон (синхрофазотрон) — ускоритель с плавно изменяющейся индукцией магнитного поля так, чтобы m/В = const.
Эффект Холла
А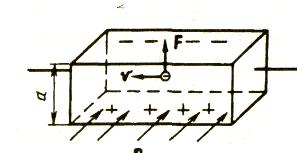 мериканский ученый Э. Холл обнаружил, что в проводнике, помещенном в магнитное поле, возникает разность потенциалов (поперечная) в направлении, перпендикулярном вектору магнитной индукции В и току I, вследствие действия силы Лоренца на заряды, движущиеся в этом проводнике.
мериканский ученый Э. Холл обнаружил, что в проводнике, помещенном в магнитное поле, возникает разность потенциалов (поперечная) в направлении, перпендикулярном вектору магнитной индукции В и току I, вследствие действия силы Лоренца на заряды, движущиеся в этом проводнике.
Опыт показывает, что поперечная разность потенциалов пропорциональна плотности тока j, магнитной индукции и расстоянию d между электродами: U = RdjB
[R — постоянная Холла, зависящая от рода вещества].
Допустим, что электроны движутся с упорядоченной средней скоростью v и на каждый электрон действует сила Лоренца, равная eBv. Под ее действием электроны смещаются так, что одна из граней образца зарядится отрицательно, другая — положительно и внутри образца возникнет электрическое поле, т. е. evB = eE.
Следовательно, поперечная разность потенциалов равна
U = Ed = vBd .
Среднюю скорость и электронов можно выразить через плотность тока у, так как j = nev, поэтому
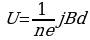
Приравнивая это выражение формуле (3.150), получаем R — 1/(пе). Постоянная Холла зависит от концентрации электронов. Измеряя постоянную R, можно определить концентрацию электронов внутри проводника.
Домашнее задание: § конспект.
Решите задачи:
Сила Лоренца
Сила Ампера, действующая на отрезок проводника длиной Δl с силой тока I, находящийся в магнитном поле B,
может быть выражена через силы, действующие на отдельные носители заряда.
Пусть концентрация носителей свободного заряда в проводнике есть n, а q – заряд носителя. Тогда произведение nqυS, где υ – модуль скорости упорядоченного движения носителей по проводнику, а S – площадь поперечного сечения проводника, равно току, текущему по проводнику:
Выражение для силы Ампера можно записать в виде:
Так как полное число N носителей свободного заряда в проводнике длиной Δl и сечением S равно nSΔl, то сила, действующая на одну заряженную частицу, равна
Эту силу называют силой Лоренца. Угол α в этом выражении равен углу между скоростью  и вектором магнитной индукции
и вектором магнитной индукции 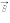 Направление силы Лоренца, действующей на положительно заряженную частицу, так же, как и направление силы Ампера, может быть найдено по правилу левой руки или по правилу буравчика. Взаимное расположение векторов
Направление силы Лоренца, действующей на положительно заряженную частицу, так же, как и направление силы Ампера, может быть найдено по правилу левой руки или по правилу буравчика. Взаимное расположение векторов  ,
, 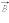 и
и 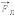 для положительно заряженной частицы показано на рис.
для положительно заряженной частицы показано на рис.
Сила Лоренца направлена перпендикулярно векторам

и
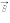
При движении заряженной частицы в магнитном поле сила Лоренца работы не совершает. Поэтому модуль вектора скорости при движении частицы не изменяется.
Если заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость  лежит в плоскости, перпендикулярной вектору
лежит в плоскости, перпендикулярной вектору 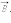 то частица будет двигаться по окружности радиуса
то частица будет двигаться по окружности радиуса
Сила Лоренца в этом случае играет роль центростремительной силы (рис. 2).
| 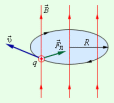
|
| Рисунок 2. Круговое движение заряженной частицы в однородном магнитном поле. |
Период обращения частицы в однородном магнитном поле равен
Это выражение показывает, что для заряженных частиц заданной массы m период обращения не зависит от скорости υ и радиуса траектории R.
Угловая скорость движения заряженной частицы по круговой траектории
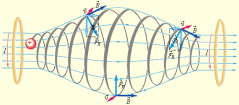
называется циклотронной частотой. Циклотронная частота не зависит от скорости (следовательно, и от кинетической энергии) частицы. Это обстоятельство используется в циклотронах – ускорителях тяжелых частиц (протонов, ионов). Принципиальная схема циклотрона приведена на рис. 3.
| 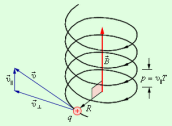
|
| Рисунок 3. Движение заряженных частиц в вакуумной камере циклотрона. |
Между полюсами сильного электромагнита помещается вакуумная камера, в которой находятся два электрода в виде полых металлических полуцилиндров (дуантов). К дуантам приложено переменное электрическое напряжение, частота которого равна циклотронной частоте. Заряженные частицы инжектируются в центре вакуумной камеры. Частицы ускоряются электрическим полем в промежутке между дуантами. Внутри дуантов частицы движутся под действием силы Лоренца по полуокружностям, радиус которых растет по мере увеличения энергии частиц. Каждый раз, когда частица пролетает через зазор между дуантами, она ускоряется электрическим полем. Таким образом, в циклотроне, как и во всех других ускорителях, заряженная частица ускоряется электрическим полем, а удерживается на траектории магнитным полем. Циклотроны позволяют ускорять протоны до энергии порядка 20 МэВ.
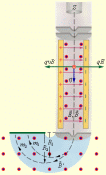
Однородные магнитные поля используются во многих приборах и, в частности, в масс-спектрометрах – устройствах, с помощью которых можно измерять массы заряженных частиц – ионов или ядер различных атомов. Масс-спектрометры используются для разделения изотопов, то есть ядер атомов с одинаковым зарядом, но разными массами (например, 20Ne и 22Ne). Простейший масс-спектрометр показан на рис. 4. Ионы, вылетающие из источника S, проходят через несколько небольших отверстий, формирующих узкий пучок. Затем они попадают в селектор скоростей, в котором частицы движутся в скрещенных однородных электрическом и магнитном полях. Электрическое поле создается между пластинами плоского конденсатора, магнитное поле – в зазоре между полюсами электромагнита. Начальная скорость  заряженных частиц направлена перпендикулярно векторам
заряженных частиц направлена перпендикулярно векторам 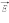 и
и 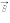
На частицу, движущуюся в скрещенных электрическом и магнитном полях, действуют электрическая сила 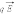 и магнитная сила Лоренца. При условии E = υB эти силы точно уравновешивают друг друга. Если это условие выполняется, частица будет двигаться равномерно и прямолинейно и, пролетев через конденсатор, пройдет через отверстие в экране. При заданных значениях электрического и магнитного полей селектор выделит частицы, движущиеся со скоростью υ = E / B.
и магнитная сила Лоренца. При условии E = υB эти силы точно уравновешивают друг друга. Если это условие выполняется, частица будет двигаться равномерно и прямолинейно и, пролетев через конденсатор, пройдет через отверстие в экране. При заданных значениях электрического и магнитного полей селектор выделит частицы, движущиеся со скоростью υ = E / B.
Далее частицы с одним и тем же значением скорости попадают в камеру масс-спектрометра, в которой создано однородное магнитное поле 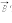 Частицы движутся в камере в плоскости, перпендикулярной магнитному полю, под действием силы Лоренца. Траектории частиц представляют собой окружности радиусов R = mυ / qB'. Измеряя радиусы траекторий при известных значениях υ и B' можно определить отношение q / m. В случае изотопов (q1 = q2) масс-спектрометр позволяет разделить частицы с разными массами.
Частицы движутся в камере в плоскости, перпендикулярной магнитному полю, под действием силы Лоренца. Траектории частиц представляют собой окружности радиусов R = mυ / qB'. Измеряя радиусы траекторий при известных значениях υ и B' можно определить отношение q / m. В случае изотопов (q1 = q2) масс-спектрометр позволяет разделить частицы с разными массами.
Современные масс-спектрометры позволяют измерять массы заряженных частиц с точностью выше 10–4.
| 
|
| Рисунок 5. Движение заряженной частицы по спирали в однородном магнитном поле. |
|
|
| Рисунок 4 Селектор скоростей и масс-спектрометр. |
Если скорость частицы

имеет составляющую
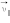
вдоль направления магнитного поля, то такая частица будет двигаться в однородном магнитном поле по спирали. При этом радиус спирали
R зависит от модуля перпендикулярной магнитному полю составляющей υ
┴ вектора
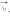
а шаг спирали
p – от модуля продольной составляющей υ
|| (рис. 5).
| 
|
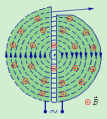
| Рисунок 6. Магнитная «бутылка». Заряженные частицы не выходят за пределы «бутылки». Магнитное поле «бутылки» может быть создано с помощью двух круглых катушек с током. |
Таким образом, траектория заряженной частицы как бы навивается на линии магнитной индукции. Это явление используется в технике для
магнитной термоизоляции высокотемпературной плазмы, то есть полностью ионизированного газа при температуре порядка 10
6 K. Вещество в таком состоянии получают в установках типа «Токамак» при изучении управляемых термоядерных реакций. Плазма не должна соприкасаться со стенками камеры. Термоизоляция достигается путем создания магнитного поля специальной конфиругации. В качестве примера на рис. 6 изображена траектория движения заряженной частицы в
магнитной «бутылке» (или
ловушке).
Аналогичное явление происходит в магнитном поле Земли, которое является защитой для всего живого от потоков заряженных частиц из космического пространства. Быстрые заряженные частицы из космоса (главным образом от Солнца) «захватываются» магнитным полем Земли и образуют так называемые радиационные пояса (рис. 7), в которых частицы, как в магнитных ловушках, перемещаются туда и обратно по спиралеобразным траекториям между северным и южным магнитными полюсами за времена порядка долей секунды. Лишь в полярных областях некоторая часть частиц вторгается в верхние слои атмосферы, вызывая полярные сияния. Радиационные пояса Земли простираются от расстояний порядка 500 км до десятков земных радиусов. Следует вспомнить, что южный магнитный полюс Земли находится вблизи северного географического полюса (на северо-западе Гренландии). Природа земного магнетизма до сих пор не изучена
Литература: -
Физика. Учебник для средних специальных учебных заведений, Жданов Л.С. В. школа 1983г.
-
Сборник задач и вопросов по физике. Гладковой Р. А.-М. 1988г.
-
Физика,10-11 классы. Гончаренко С. У. Образование 1996 г.
-
Савельев Курс общей физики М. Просвещение 1988 г.
-
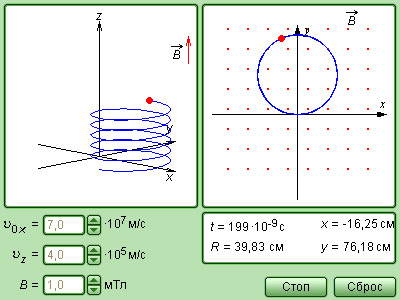 |
| Модель. Движение заряда в магнитном поле |

| 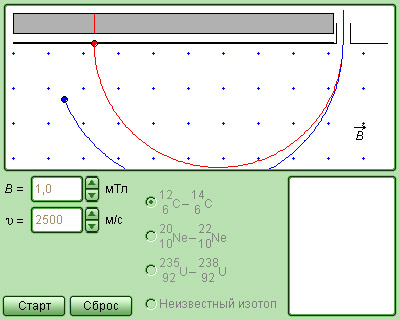 |
| Модель. Масс-спектрометр |

| 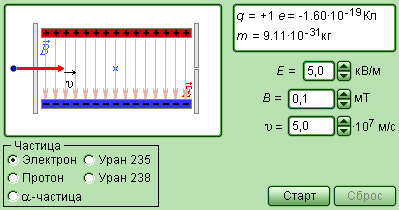 |
| Модель. Селектор скоростей |









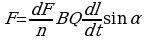
 сли a = 0, sina = 0, то Рл = 0, т. е. если частица движется так, что вектор скорости v параллелен вектору магнитной индукции В, то со стороны магнитного поля сила не действует.
сли a = 0, sina = 0, то Рл = 0, т. е. если частица движется так, что вектор скорости v параллелен вектору магнитной индукции В, то со стороны магнитного поля сила не действует.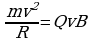
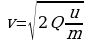
 Ускорители заряженных частиц
Ускорители заряженных частиц  з этой формулы легко получить выражения для угловой скорости и периода вращения частицы:
з этой формулы легко получить выражения для угловой скорости и периода вращения частицы: мериканский ученый Э. Холл обнаружил, что в проводнике, помещенном в магнитное поле, возникает разность потенциалов (поперечная) в направлении, перпендикулярном вектору магнитной индукции В и току I, вследствие действия силы Лоренца на заряды, движущиеся в этом проводнике.
мериканский ученый Э. Холл обнаружил, что в проводнике, помещенном в магнитное поле, возникает разность потенциалов (поперечная) в направлении, перпендикулярном вектору магнитной индукции В и току I, вследствие действия силы Лоренца на заряды, движущиеся в этом проводнике.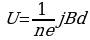
 и вектором магнитной индукции
и вектором магнитной индукции 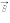 Направление силы Лоренца, действующей на положительно заряженную частицу, так же, как и направление силы Ампера, может быть найдено по правилу левой руки или по правилу буравчика. Взаимное расположение векторов
Направление силы Лоренца, действующей на положительно заряженную частицу, так же, как и направление силы Ампера, может быть найдено по правилу левой руки или по правилу буравчика. Взаимное расположение векторов 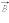 и
и 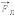 для положительно заряженной частицы показано на рис.
для положительно заряженной частицы показано на рис.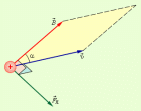
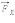 Модуль силы Лоренца
Модуль силы Лоренца 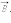 помноженной на заряд q.
помноженной на заряд q.

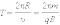
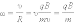

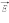 и
и 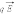 и магнитная сила Лоренца. При условии E = υB эти силы точно уравновешивают друг друга. Если это условие выполняется, частица будет двигаться равномерно и прямолинейно и, пролетев через конденсатор, пройдет через отверстие в экране. При заданных значениях электрического и магнитного полей селектор выделит частицы, движущиеся со скоростью υ = E / B.
и магнитная сила Лоренца. При условии E = υB эти силы точно уравновешивают друг друга. Если это условие выполняется, частица будет двигаться равномерно и прямолинейно и, пролетев через конденсатор, пройдет через отверстие в экране. При заданных значениях электрического и магнитного полей селектор выделит частицы, движущиеся со скоростью υ = E / B.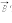 Частицы движутся в камере в плоскости, перпендикулярной магнитному полю, под действием силы Лоренца. Траектории частиц представляют собой окружности радиусов R = mυ / qB'. Измеряя радиусы траекторий при известных значениях υ и B' можно определить отношение q / m. В случае изотопов (q1 = q2) масс-спектрометр позволяет разделить частицы с разными массами.
Частицы движутся в камере в плоскости, перпендикулярной магнитному полю, под действием силы Лоренца. Траектории частиц представляют собой окружности радиусов R = mυ / qB'. Измеряя радиусы траекторий при известных значениях υ и B' можно определить отношение q / m. В случае изотопов (q1 = q2) масс-спектрометр позволяет разделить частицы с разными массами.
 Если скорость частицы
Если скорость частицы 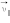 вдоль направления магнитного поля, то такая частица будет двигаться в однородном магнитном поле по спирали. При этом радиус спирали R зависит от модуля перпендикулярной магнитному полю составляющей υ┴ вектора
вдоль направления магнитного поля, то такая частица будет двигаться в однородном магнитном поле по спирали. При этом радиус спирали R зависит от модуля перпендикулярной магнитному полю составляющей υ┴ вектора 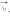 а шаг спирали p – от модуля продольной составляющей υ|| (рис. 5).
а шаг спирали p – от модуля продольной составляющей υ|| (рис. 5). 























