| 2. Актуализация теоретических знаний и фиксирование индивидуального затруднения в пробном учебном действии (4-5 мин). Открываем тетради, записываем число, оставьте место под тему урока. Мы запишем её позже. -Давайте с вами вспомним, чем мы занимались на прошлом уроке. -Правильно, поэтому я предлагаю вам решить следующие неравенства, устно проговаривая алгоритм решения. (слайд 3) Решить неравенства: x2-2x-80 Цель задания: вспомнить алгоритм решения квадратичного неравенства - Что мы делаем на первом шаге?
-Что можно сказать про эту функцию?
-Правильно, следующий шаг?
|
-учащиеся открывают тетради, записывают число
-решали квадратичные неравенства
-записывают решение неравенств в тетрадях, устно проговаривая алгоритм решения
-Рассматриваем квадратичную функцию 1. y= x2-2х -8 -её графиком является парабола, ветви которой направлены вверх
-Решаем квадратное уравнение 2. x2-2x-8=0 - По теореме Виета- |
| -Как можно решить данное уравнение? -Проговорите, пожалуйста, решение.
-Молодцы, что мы делаем на третьем шаге
-Точки будут закрашенные или выколотые и почему?
-Дальше что делаем? -Промежутки с какими знаками запишем в ответ и почему? -Числа -4 и 2 включаем или нет? -Правильно, молодцы, продиктуйте ответ. -У кого есть вопросы по решению данного неравенства?
-Следующее неравенство (слайд 4) (x-2)(x+3) 0 Цель задания: подготовить учащихся к изучению новой темы – вспомнить разложение квадратного трехчлена на множители -Как можно решить данное неравенство?
- Правильно, решаем.
-Записываем квадратичную функцию 1) y= x2+x-6, -Что про неё можно сказать? -Ребята, обратите внимание на подчеркнутые выражения, что мы с вами получили? - Значит, что можно сразу найти? -Записываем квадратное уравнение и его корни 2) x2+x-6=0 x1=2, x2=-3 -Дорешайте самостоятельно это неравенство
Какой ответ получили? - Давайте проверим (на слайде появляется решение неравенства) 3. Выявление места и причины затруднения. А теперь решим следующее неравенство (слайд 5) (x-2)(x-3)(х-4) ˃0 Цель задания: показать актуальность изучения новой темы путем создания проблемной ситуации.
- Ребята, сможем ли мы решить данное неравенство предыдущим способом? - Давайте попробуем выяснить где именно возникло затруднение и почему?
- Как решать такое неравенство? Перебирать все возможные комбинации плюсов и минусов? Рисовать график — тоже не вариант, поскольку непонятно, как ведет себя такая функция на координатной плоскости. Для таких неравенств нужен специальный алгоритм решения, который является универсальным способом решения неравенств, и называется метод интервалов. С его помощью вы сможете решить любое неравенство. Даже если вы забудете способ, которым решается то или иное неравенство, то всегда сможете им воспользоваться
- Сформулируйте тему нашего урока
4. Постановка учебной задачи (4-5 мин). Цели для учителя: -создание условий для постановки учебной задачи. Для учащихся: -выявление места и причины затруднения, постановка цели урока
-Что нужно сделать, чтобы преодолеть возникшее затруднение?
- Какая же будет цель нашей деятельности на уроке сегодня? Цель урока: выработать алгоритм решения неравенств методом интервалов и рассмотреть его применение на примерах. 5. «Открытие» учащимися нового знания. (7-8 мин). Цели для учащихся: -выбор способа решения учебной задачи; -выдвижение и обоснование гипотезы. Для учителя: - фиксирование в речи и знаково нового способа действий. - Для решения данного неравенства, мы с вами, будем использовать метод интервалов. Что такое метод интервалов? Метод интервалов — это специальный алгоритм, предназначенный для решения сложных неравенств вида f (x) 0 и f (x) (слайд 7) 1. как и в предыдущих случаях, мы должны решить соответствующее уравнение. (х-2)(х-3)(х-4)=0 -Как решается данное уравнение?
2. Отмечаем полученные корни на координатной прямой. Какие будут точки? Таким образом, прямая разделится на несколько числовых промежутков (интервалов), назовите их
Выясняем знак (плюс или минус) неравенства f (x) на самом правом интервале. Для этого достаточно подставить в f (x) любое число, которое будет правее всех отмеченных корней; Далее на координатной прямой знаки на остальных интервалах. Для этого достаточно запомнить, что при переходе через каждый корень знак меняется. Выписать интервалы, которые нас интересуют. Так как знак неравенства « », то выбираем промежутки со знаком «+ », если бы был знак неравенства « Ответом будет объединение этих промежутков -С помощью данного метода можно решить неравенство любой степени, в том числе и второй, которые мы с вами решали с помощью схематического построения параболы. - У вас на столах лежат памятки, которые вы вклеите в свои тетрадки для теории. В этой памятке приведен алгоритм решения неравенств с помощью метода интервалов в общем виде. -Давайте с вами прочитаем этот алгоритм (Слайд 8) Физкультминутка | 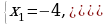 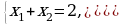
- Отмечаем полученные корни на оси Ох и через отмеченные точки схематично строим график параболы -выколотые, потому что знак неравенства строгий
3.  + - + + - +
   -4 2 Х -4 2 Х
- Расставляем знаки на промежутках - Промежутки со знаком +, потому что в неравенстве стоит знак -Нет, потому что знак неравенства строгий 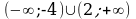 -Ответ: -Ответ:
(задают, если есть, вопросы)
«Круг идей» - ученики выдвигают гипотезы -если мы раскроем скобки, то получим квадратное неравенство и решим его, аналогично предыдущему примеру.
(у доски решает один ученик) -(x-2)(x+3)= x2+3x-2x-6= x2+x-6
- её графиком является парабола, ветви которой направлены вверх - Разложение квадратного трехчлена на множители
-Корни квадратного уравнения
(записывают решение неравенства в тетради)
(зачитывают свой ответ)
(самопроверка)
-нет,
-потому, что после раскрытия скобок мы получаем неравенство третьей степени, а мы умеем решать только линейные и квадратичные.
«Решение неравенств методом интервалов»
- изучить метод интервалов и научиться применять его для решения неравенств.
- выработать (сформулировать) алгоритм решения неравенств методом интервалов.
Учащиеся отвечают на вопросы учителя и работают с карточками «Заполни пропуски»
x-2=0 x-3=0 x-4=0
x=2 x=3 x=4
   
  
4 3 2 X
(-;2) (2;3) (3;4) (4;+)
        3 4 2 - + - + X

Ответ: (2;3)(4;+)
Читают алгоритм |
| 5. Первичное закрепление (4-5 мин). Цели для учителя: -создание условий для первичного закрепления. Для учащихся: -усвоение нового способа действий. -Нам надо решить неравенства методом интервалов. Кто хочет рассказать, как это надо сделать? Первое неравенство (х+3)(х-4)(х-7) 0.
Второе неравенство (х2-9)(х+5) ≤ 0.
6. Самостоятельная работа в парах c взаимопроверкой по эталону (4-5 мин). Цели для учителя: -создание условий для интериоризации (переход извне внутрь) нового способа действий; -создание ситуации успеха. Для учащихся: -индивидуальная рефлексия достижения цели.
7. Включение в систему знаний и повторение (7-8 мин). Цели для учителя: -создание условий для включения «открытия» в систему знаний, повторение и закрепление ранее изученного. Для учащихся: -включение «открытия» в систему знаний, повторение и закрепление ранее изученного. - А сейчас, я предлагаю разобрать задания, где пригодятся полученные сегодня знания. Разбейтесь на 4 группы (по геометрическим фигурам, лежащим у каждого на парте) - Оцените свою работу в группе по 5-ой шкале.
8. Рефлексия учебной деятельности на уроке (итог урока) (2-3 мин). Цели для учителя: -создание условий для рефлексии учебной деятельности учащихся на уроке. - И вспомним начало нашего урока. Удалось ли нам достигнуть поставленных целей? С каким новым методом решения неравенств мы сегодня познакомились? -Какова была цель сегодняшнего урока? -Как вы думаете, мы достигли поставленной цели? -Неравенства какой степени мы теперь можем решать? - Ян Амос Коменский говорил: «Считай несчастным тот день или тот час, в который ты не усвоил ничего нового, ничего не прибавил к своему образованию». Я надеюсь, что в сегодняшнем уроке вы найдете для себя хоть крупинку полезного.
У каждого из вас на столе мишки. Уходя из класса, прикрепите на доску одного из них. Мишка зеленого цвета обозначает: “Я удовлетворён уроком, урок был полезен для меня, я много, с пользой и хорошо работал на уроке”. Мишка желтого цвета обозначает: “Урок был интересен, я принимал в нём активное участие, я сумел выполнить ряд заданий, мне было на уроке достаточно комфортно”. Мишка розового цвета обозначает: “Я получил пользу от урока, но мне не все удалось выполнить правильно, домашнее задание я выберу среднего уровня 9. Домашнее задание (2 мин) Ваше домашнее задание нескольких уровней. Каждый выбирает уровень себе по силам.
|
«Обучая - учусь»
Решение: 1. Найти корни уравнения - x1=-3, x2=4, x3=7, - 2.Отметить на числовой прямой корни -выколотые - 3.Определить знак выражения на каждом из получившихся промежутков - Определить знак каждого множителя на каждом из промежутков (чертят таблицу знаков) (диктует знаки) - 4. Записать ответ, выбрав промежутки с соответствующим знаку неравенства знаком -промежутки со знаком +, потому что знак неравенства 0 Ответ: (-3;4) 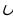 (7; +∞). (7; +∞).
Учащиеся решают самостоятельно, с последующей взаимной проверкой по эталону (Слайд 9) Ответ: (-∞;-5] 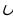 [-3;3]. [-3;3]. « Тайный конверт» Каждая пара получает закрытый конверт с заданием, аналогичным одному из рассмотренных примеров и решает поставленную задачу, а затем выполняется самопроверка работы по образцу – (слайд 10) Задания: 1) (х + 7)(х + 2)(4 – х)(2х – 10) ≥ 0. ( x Є [-7; -2] U [4; 5] ) 2) (х + 2)(х2 – 9) (х Є (- ∞; -3) U (-2; 3) ) 3) (х2 + 4х – 5)(х+7)(х + 3) ≥ 0 (х Є (- ∞; -7] U [-5; -3] U [1; + ∞) ) 4) (х + 4)(х + 1)(х – 1)(х – 8) ≥ 0 (х Є (- ∞; - 4] U [-1;1] )
«Работа в группах» Задание для групп № 1,2: № 677(1,3) Задание для групп № 3,4: № 677(2,4)
- Методом интервалов
- Научиться решать неравенства методом интервалов
- Да
- Неравенства любой степени
Решить неравенства методом интервалов Средний уровень 1) х2 – 7х + 12 ≤ 0 2) (х + 10)(х – 4) 3) 2х (8 + х)(х – 12) 0 4) (х + 2)(7 – х)(х – 13) 0 5) (х + 5)/(х - 6) 0 Достаточный уровень 1) (х – 2)(х +5)/(х + 2) ≥ 0 2) (х + 3)2(х + 1)(х – 2) ≤ 0 3) (16 – х2)(3х2 + 1) 0 4) (6 – 3х)/(х + 4) ≥ 0 Высокий уровень 1) (х4 – 16х2)( - х2 – 5) ≤ 0 2) (– х2 + 8х – 7)/(х2 + х – 2) 0 3) х3 – 5х2 + 6х ≥ 0 4) (х – 2)(х + 2)2(х + 3)/(х - 1) ≤ 0
|






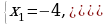
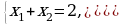
 + - +
+ - +

 -4 2 Х
-4 2 Х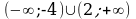 -Ответ:
-Ответ:




 (7; +∞).
(7; +∞). 









