Республиканский конкурс методических разработок и проектов
«Учитель – профессия дальнего действия»
Методическая разработка
«Площадь криволинейной трапеция и интеграл»
(Применение метода рецензирования для всесторонней проверки знаний учащихся)
Автор:
Загиров Нариман Рашидович
Место работы:
МБОУ «Чинарская СОШ №2 имени М.М.Гусаева»
Контактный телефон:
8960419255
Адрес электронной
[email protected]
Пояснительная записка.
«Скажи мне – и я забуду.
Покажи мне – и я запомню,
Вовлеки меня – и я научусь».
(Конфуций)
После окончания университета, и изучения многих дисциплин в теории, перед молодым учителем встает вопрос: «Какую методику выбрать для улучшения качества знаний учащихся?». Изучая и анализируя научно-методическую литературу, обобщая опыт коллег, наблюдая детей на своих уроках я, испытав многие из современных технологий, в своей педагогической деятельности стал использовать технологии:
разноуровневого обучения
исследовательские технологии
опорного конспектирования
современные компьютерные технологии
Целями современного школьного образования должны стать:
научить учится, т.е. научить решать проблемы в сфере учебной деятельности;
научить искать нестандартные подходы решения задач:
воспитать достойного гражданина страны.
Исходя из этого, ставлю перед собой следующие задачи:
• обеспечить качественное образование по математике для каждого учащегося;
• реализовать принципы разноуровневого и исследовательского подхода в процессе преподавания математики;
• конструировать системы уроков с использованием традиционных и нетрадиционных методов и форм обучения;
• развить устойчивое внимания учащихся на уроках путем стимулирования познавательного интереса различными методами и приемами;
«Разных детей и учить надо по-разному, потому что каждый по-своему воспринимает информацию» (Гарднер) [2]. Именно поэтому важно применять разноуровневое обучение.
Учащимся на выбор даются карточки с разными цветами и разной сложности (Приложение 1). Зеленая карточка (легкие задания) на оценку три, желтая карточка (средней сложности) на оценку четыре и красная карточка (трудные задания) на оценку пять. Заядливые «троечники», которые ничего не делают при стандартных карточках, вовлекаются в работу. Здесь они работают и получают заслуженную оценку.
Контрольные работы. Задания распределены по трем уровням сложности А, В, С. Уровень А соответствует обязательным программным требованиям, В - среднему уровню сложности, задания уровня С предназначены для учеников, проявляющих повышенный интерес к математике. Обучающиеся могут сравнить задания различных уровней и, с разрешения учителя, выбрать подходящий для себя уровень сложности.
В качестве исследовательской технологии провожу метод рецензий. Учащимся дается на дом определенная тема. На следующем уроке, методом случайного отбора, выбираются несколько пар - докладчик и рецензент (Например: тех, у кого нет оценок) (Приложение 2). Докладчик отвечает или решает у доски, а рецензент следит за выступлением первого, задает «каверзные» вопросы, ищет неправильные ответы и решения. Данную методику можно использовать при использовании «перевернутого класса» (Приложение 3).
Возрастает:
интерес к учебе, за счет поиска дополнительной литературы.
мотивация, за счет здоровой конкуренции.
Оцениваются оба. Оцениваю не только знания, но и другие показатели:
участие в дискуссиях;
умение высказывать свою точку зрения;
сбор материала из различных источников;
активность при обсуждении вопросов;
умение задавать вопросы;
возможность выразить свое отношение к изучаемому материалу.
В работе также активно использую составление краткого опорного конспекта (Приложение 4). Например: на первых уроках геометрии в 7 классе ребята знакомятся с различными простейшими фигурами. Появляется новая терминология, которая нелегко усваивается ими. Опорные конспекты помогают выучить много разных определений и формул легко и просто.
Такой вид деятельности, как применение ИКТ на уроках, расширяет творческий потенциал участников образовательного процесса, позволяет выйти за рамки традиционной модели изучения математики. Появляется мотивация к самообразованию. Проведение уроков с использованием ИКТ дает весомые дидактические преимущества по сравнению с традиционным: создается обучающая среда с ярким и наглядным представлением информации, что особенно привлекает обучающихся, и способствует повышению заинтересованности к обучению. Презентации по таким сложным темам как «Применение производной для исследования функций» (10 кл), «Объёмы тел» (11 кл) значительно улучшают понимание и усвоение материала учащимися. Использование ИКТ на уроках позволяет дифференцировать и индивидуализировать процесс усвоения знаний. Информация, представленная в электронном виде, легко обновляема, а, следовательно, всегда актуальна.
У. У. Сойер в книге "Прелюдия к математике" пишет: "Можно научить учеников решать достаточно много типов задач, но подлинное удовлетворение придет лишь тогда, когда мы сумеем передать нашим воспитанникам не просто знания, а гибкость ума", которая дала бы им возможность в дальнейшем не только самостоятельно решать, но и ставить перед собой новые задачи.
Площадь криволинейной трапеция и интеграл.
Тема урока: «Площадь криволинейной трапеция и интеграл».
Цель урока:
Ознакомить учащихся с понятиями: криволинейная трапеция и интеграл.
Вычисление площади криволинейной трапеции, введением понятия определённого интеграла, и его расчет по формуле Ньютона-Лейбница, используя знания о первообразной и правил её вычисления.
Задачи:
1. Проиллюстрировать практическое применение интеграла на примерах нахождения площади криволинейной трапеции.
2. Обобщить и систематизировать знания, проверить усвоение изученного материала
3. Закрепить изученное в ходе выполнения упражнений.
Планируемые результаты:
Предметные: знать понятии: криволинейная трапеция, интеграл; вычислять площадь криволинейной трапеции; научится вычислять интегралы.
Метапредметные:
Регулятивные –стремиться выполнить учебную задачу; осуществлять оценку действий;
Познавательные – работать с опорным конспектом; ориентироваться в материале, находить нужную информацию;
Коммуникативные – приводить доводы и отстаивать свои знания и точку зрения;
Личностные – формирование понимания возможностей применения интеграла.
Оборудование: интерактивная доска (HITACHIStarBoard), компьютер, карточки.
ХОД УРОКА.
Мотивирование.
- Здравствуйте ребята! Есть у нас отсутствующие? (Узнать причины).
- Ребята мы начинаем урок. Повернитесь к своему соседу, поздоровайтесь и улыбнитесь друг другу.
- Посмотрите на слайд (На слайде цитата: «Ни одно великое открытие не было сделано без смелой догадки». - Исаак Ньютон). Как вы это понимаете… Давайте это обсудим… (Дети выражают свои мнения..)
2) Проверка домашнего задания.
а) - Ребята все ли выполнили домашнее задание? (Узнаем причины невыполнения домашнего задания). Пройтись по рядам и проверить правильность выполнения домашнего задания. Даем оценку выполненных работ (Не скупимся на комментарии выполненных работ).
б) - Ребята, теперь проверим, на сколько хорошо вы помните пройденный материал. (Фронтальный опрос)
Чему равно производная: х5, lnx, 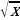 , 9, х-3, sin3x.
, 9, х-3, sin3x.
Наидите первообразную: х2, 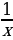 , cos x, 5х.
, cos x, 5х.
3) Всесторонняя проверка знаний.
а) – Ребята, теперь проверим на сколько хорошо вы усвоили тему «Применение производной». У меня карточки трех уровней сложности. Выбирайте по вашему желанию. С карточками работают: Маджидов М., Алиев Ш., и Таибов Э.. Выбирайте карточки.
б) - На проверку знаний по рецензированию приглашаются Авчиев Т., Юсуфджамалова Х., Кахриманов К. и Багомедов Н.. у меня в руках карточки одинакового цвета, внутри разные фигуры. Доставшие одинаковые фигуры образуют пары. Тяните карточку, выбирем пары и кто будет рецензентом, а кто докладчиком. (Выбрать, случайным образом, две пары выступающих и их рецензентов). Первая пара работает по теме производная, а вторая по теме первообразная.
- Рецензенты садитесь на свои места и внимательно следите за работой докладчика. Подготовьте вопросы.
в) С остальным классом работаем по учебнику.
- Ребята, откройте стр 296. Выполняйте самостоятельно упр №993 [1] (Учащиеся решают задания. Учитель проходит по классу и дает рекомендации к выполнению заданий).
г) - Кто закончил (Работаем с тем, кто уже закончил. Проверяем и ставим оценки. За это время, завершают свои работы и остальные учащиеся).
д) - Время на подготовку завершено. Докладчик объясняет решение, рецензент внимательно слушает и задает вопросы. (В зависимости от того, как грамотно отвечают докладчик и рецензент ставят оценки обоим (Приложение 4). Таким же образом отвечают вторая пара).
4) Объяснение новой темы.
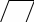


 а) – Ребята, какие фигуры изображены на экране.
а) – Ребята, какие фигуры изображены на экране.
 - А как вы назовете эту фигуру?
- А как вы назовете эту фигуру?
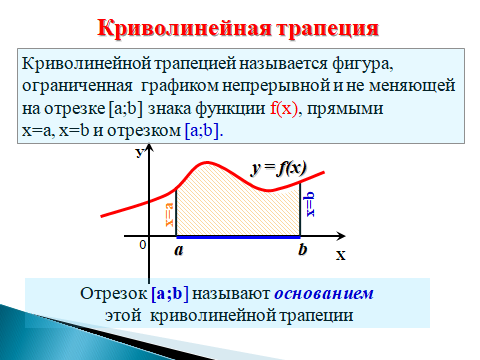
- Что такое трапеция? Напоминает ли эта фигура трапецию? (Задаем сопутствующие вопросы. Напоминает ли фигура трапецию? Как называется верхняя линия? Учащиеся уже сами называют фигуру криволинейной трапецией). Криволинейная трапеция, объяснение понятия, демонстрация (Слайд 1).
б) Площадь криволинейной трапеции.
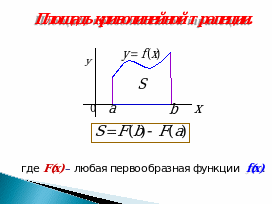
1) объяснение понятия, демонстрация (Слайд 2).
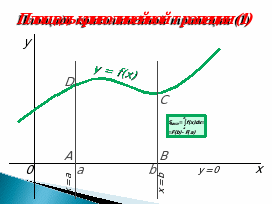
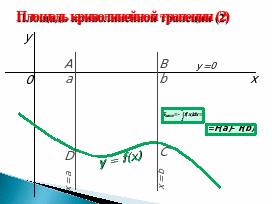
2) Работа с классом (Слайды 3-5).
в) Интеграл и формула Ньютона-Лейбница.
1) Объяснение понятия, демонстрация (Слайд 6).
2) - Ребята, мы прошли основные понятия новой темы. Какая тема нашего урока? (Учащиеся сами приходят к теме и целям урока).
3) Воспитательная часть (История Ньютона).
- Ребята, а вы знали, что Исаак Ньютон сначала плохо учился. Когда его одноклассник назвал его неучем, он начал учится хорошо. К концу четверти он обогнал по оценкам этого мальчика, а затем и остальных сверстников. За свои труды его возвели в ранг лорда, и похоронен он, человек из бедной семьи, с монархами в Вестми́нстерском аббатстве. Всякого кто будет учится и работать над собой ждет только светлое будущее. Не упускайте время и учитесь хорошо.
3) Вычисление площадей (Слайды 7-9).
г) Тема рецензирования.
- Ребята! Тема рецензирования показана на экране. Чтобы подготовиться к этой теме вам нужно прочитать не только учебник, но и дополнительную литературу. Ишите информацию и в интернете .Например на сайте ПостНаука. (Слайд 10).
5) Закрепление темы
а) Составление опорного конспекта.
(Составляем краткий опорный конспект (100-150 слов). Криволинейная трапеция, интеграл, определенный интеграл, формула Ньютона-Лейбница).
б) Фронтальный опрос с вызовом к доске.
(Вызываем к доске учашихся, из числа желающих, для объяснения тех терминов, понятий и формул которые прошли на уроке. Учащиеся по памяти сформулируют определения из опорного конспекта).
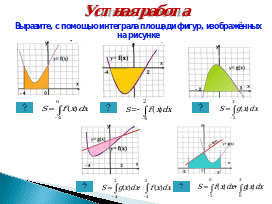
в) Устная работа (Слайд 11).
6) Рефлексия.
- Ребята, наш урок приближается к концу, если вам понравился урок, то поднимите руку большим пальцем вверх, иначе – пальцем вниз. Спасибо.
7) Домашнее задание.
1) §53. [1]
2) А 999 (3,4); 1001(1); [1]
В 999 (3,4); 1001; [1]
С 999 (3,4); 1001; 1003; [1]
- Запишите домашнее задание в дневники. Запишите домашнее задание в дневники. Посмотрите на уровень заданий. Выполняете тот уровень, на какую оценку рассчитываете. Поменяйтесь дневниками с соседом. Проверьте правильность заполнения домашнего задания.
Список использованной литературы.
Алгебра и начала математического анализа. 10-11 кл. Ш. А. Алимов, Ю.М. Колягин, М, В, Ткачева и др. Просвещение, 2016 г.
Анализ урока. Ю, А, Конаржевский. Центр «Педагогический поиск», 2003 г.
МАТЕМАТИКА. Реализация требований ФГОС основного общего образования. Л. О. Рослова, Е. Е. Алексеева, Е. В. Буцко ; под ред. Л. О. Рословой. ФГБНУ «Институт стратегии развития образования РАО», 2022 г.
Информационные и коммуникационные технологии в образовании [материал из IrkutskWiki]. - Режим доступа: http://www.wiki.irkutsk.ru/index.php/.
Апатова Н.В. Информационные технологии в школьном образовании. - М., 1994.
В. Волков. Современные мультимедиа // Компьютер-ИНФО,
Приложения.
Приложение 1.
| 1 5 7 5 7 6 5 5 2 8 1 5 2 5 | Найти одну первообразную функции. 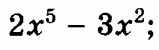
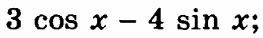
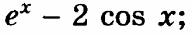
|
| 1 5 7 5 7 6 5 5 2 8 1 7 5 8 7 7 | Найти одну первообразную функции. 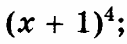
Найти все первообразные функции. 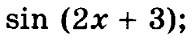
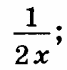
|
| 1 х х э 5 э 7 ю ю ю э 5 7 6 5 5 2 8 1 7 5 8 7 9 | 1) Найти все первообразные функции. 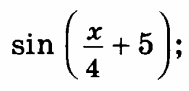 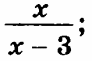
2) 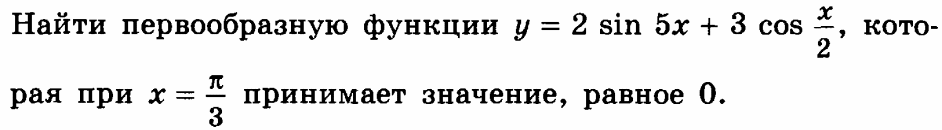
|
Приложение 2.
Приложение 3.
Приложение 4 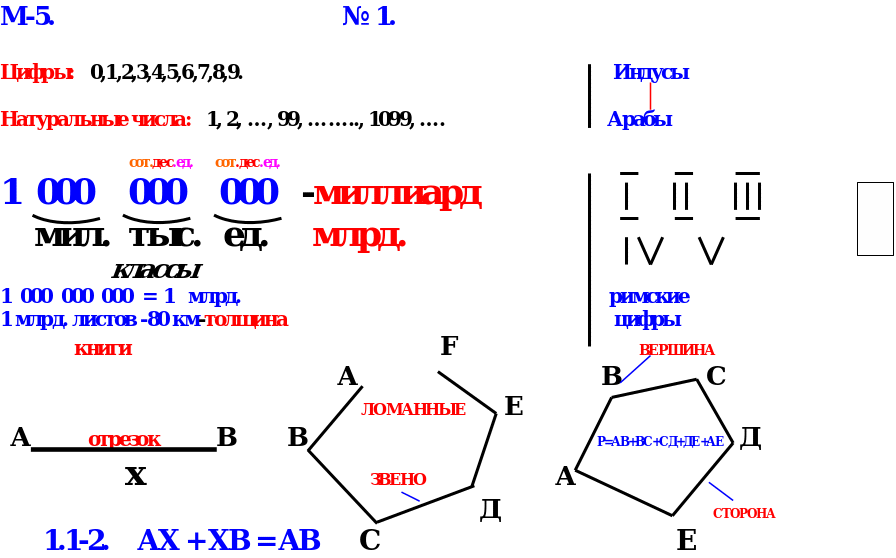
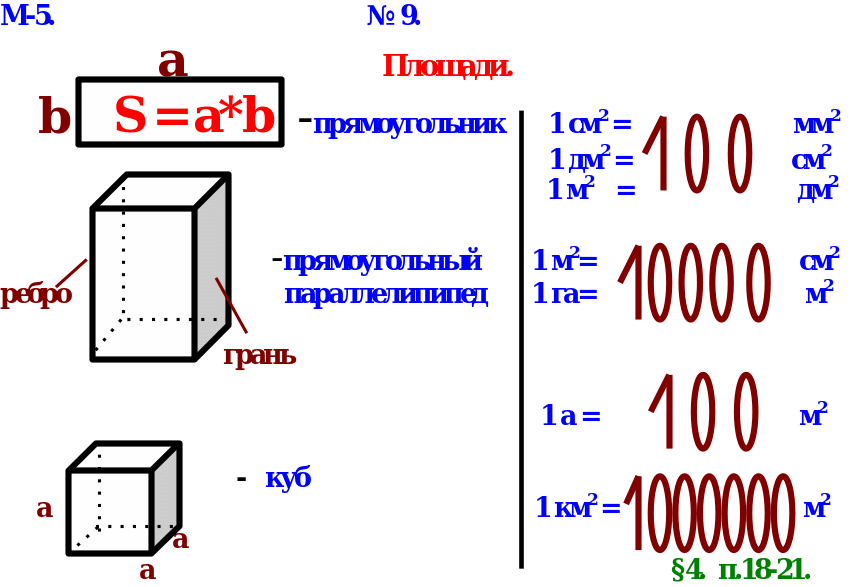
Слайд 1
Слайд 2
Слайд 3
Слайд 4
Слайд 5
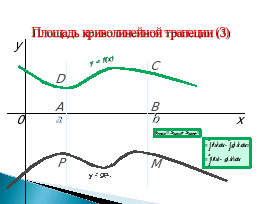
Слайд 6

Слайд 7
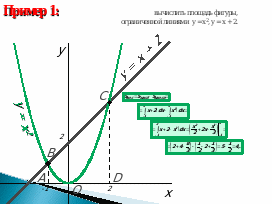
Слайд 8
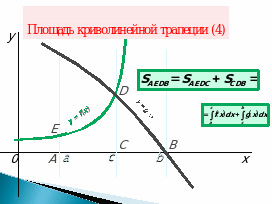
Слайд 9
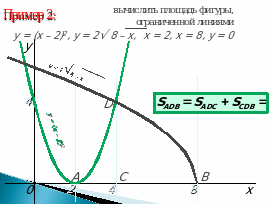
Слайд 10

Слайд 11
10






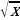 , 9, х-3, sin3x.
, 9, х-3, sin3x.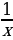 , cos x, 5х.
, cos x, 5х.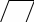


 а) – Ребята, какие фигуры изображены на экране.
а) – Ребята, какие фигуры изображены на экране. - А как вы назовете эту фигуру?
- А как вы назовете эту фигуру?