Методическая разработка по теме
«Линейная функция. Линейные уравнения и неравенства с параметрами».
Линейная функция и линейное уравнение – одна из основных тем школьного курса математики. Введение понятий «параметр, решение задача с параметрами» в этой теме следует начинать с пропедевтики: повторения понятий постоянной и переменной величин и выделении из множества переменных параметров.
В курсе алгебры учащиеся изучают понятия, оперирующие с двумя видами величин – постоянными и переменными. Переменные величины, в свою очередь, можно условно разделить на приоритетные – аргументы, искомые и остальные – параметры. Данное разделение можно представить в виде следующей схемы:
| Постоянные: 1,2, 3,… |
| Переменные: 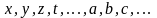 |

| Приоритетные переменные - аргументы |
| Параметры |
Определение. Параметром называется независимая переменная величина, входящая в условие задачи или появляющаяся в процессе ее решения, «управляющая» решением задачи.
Таким образом, имеем:
Все входящие в данное уравнение или неравенство переменные равноправны и каждая из них может быть объявлена неизвестной (аргументом).
Все оставшиеся переменные объявляются параметрами, которым присваиваются по умолчанию некоторые числовые значения, входящие в область определения данного аналитического выражения.
Объявление тех или иных переменных аргументами или параметрами определяется условиями поставленной задачи или методами, пригодными для ее анализа и решения.
Р еализация представленного разделения может отрабатываться в системе упражнений, подобных следующему:
еализация представленного разделения может отрабатываться в системе упражнений, подобных следующему:
Упражнение 1.
Укажите постоянные и переменные величины, входящие в уравнения:
1) 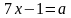 6)
6) 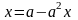
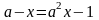 7)
7) 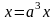
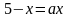 8)
8) 
 9)
9) 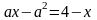
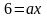 10)
10) 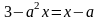
Упражнение 2.
Даны уравнения, линейные относительно переменной  . Укажите уравнения, содержащие и не содержащие параметры.
. Укажите уравнения, содержащие и не содержащие параметры.
 6)
6) 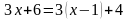
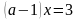 7)
7) 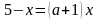
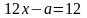 8)
8) 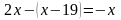
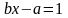 9)
9) 
 10)
10) 
Пример 1.
1) Найдите все значения параметра , при которых уравнение
, при которых уравнение  является линейным.
является линейным.
2) Будет ли это уравнение линейным относительно переменной  ?
?
Решение. 1) Выбрав переменную  в качестве параметра, мы тем самым оставили переменную
в качестве параметра, мы тем самым оставили переменную  в качестве неизвестной. Уравнение
в качестве неизвестной. Уравнение  будет линейным относительно переменной
будет линейным относительно переменной  , если коэффициент при второй степени переменной
, если коэффициент при второй степени переменной  будет равен 0. Следовательно, параметр
будет равен 0. Следовательно, параметр должен быть равен 0. Ответ: 0.
должен быть равен 0. Ответ: 0.
Так как наибольшая степень переменной  равна 1, то уравнение является линейным относительно переменной
равна 1, то уравнение является линейным относительно переменной  при всех действительных значениях параметра
при всех действительных значениях параметра  .
.
Определение. Значение параметра называется допустимым, если для него существует хотя бы одно значение переменной  , при одновременной подстановке которых в уравнение левая часть уравнения определена, т.е. имеет смысл.
, при одновременной подстановке которых в уравнение левая часть уравнения определена, т.е. имеет смысл.
Рассмотрим достаточно подробно решение следующих задач:
Задача 1. Решите уравнение  при всех значениях параметра
при всех значениях параметра  .
.
Решение. Дано простейшее уравнение относительно переменной  с параметром
с параметром  . Решить его – это значит:
. Решить его – это значит:
Указать, при каких допустимых значениях параметра  уравнение имеет решения, и найти вид этих решений в зависимости от значений параметра
уравнение имеет решения, и найти вид этих решений в зависимости от значений параметра  .
.
Указать, при каких допустимых значениях параметра уравнение не имеет решений.
Согласно общей схеме анализа решения линейного уравнения, получим:
Уравнение имеет смысл при любых значениях параметра.
Если  , то уравнение имеет единственное решение
, то уравнение имеет единственное решение  .
.
Если  , то равенство
, то равенство  невозможно ни при каких значениях переменной
невозможно ни при каких значениях переменной  , следовательно, уравнение решений не имеет.
, следовательно, уравнение решений не имеет.
Ответ: При  решением уравнения является число
решением уравнения является число  . При
. При  уравнение решений не имеет.
уравнение решений не имеет.
Задача 2. Решите уравнение 
Решение.  ;
;  ;
;  .
.
Если  , т.е.
, т.е.  , то уравнение имеет единственное решение
, то уравнение имеет единственное решение 
Если  , то уравнение обращается в равенство
, то уравнение обращается в равенство  , которому удовлетворяет любое действительное значение переменной
, которому удовлетворяет любое действительное значение переменной  .
.
Ответ: Если  , то
, то  . Если
. Если  , то решением является любое действительное число.
, то решением является любое действительное число.
Задача 3. При каком значении параметра  уравнение
уравнение  не имеет решения?
не имеет решения?
Решение. Так как переменная  определена как параметр, то имеем уравнение относительно переменной
определена как параметр, то имеем уравнение относительно переменной  :
:  . Так как правая часть уравнения отлична от нуля, то уравнение не будет иметь решений, если коэффициент при
. Так как правая часть уравнения отлична от нуля, то уравнение не будет иметь решений, если коэффициент при  будет равен нулю. Это возможно лишь при
будет равен нулю. Это возможно лишь при  .
.
Ответ:  .
.
Задача 4. При каком значении параметра  уравнение
уравнение  обращается в тождество?
обращается в тождество?
Решение. Запишем уравнение в виде  . Так как правая часть уравнения равна 0, то уравнение обратится в тождество, если коэффициент при неизвестной
. Так как правая часть уравнения равна 0, то уравнение обратится в тождество, если коэффициент при неизвестной  также будет равен 0. А это возможно, если
также будет равен 0. А это возможно, если  .
.
Ответ:  .
.
Задача 5. Решите уравнение  .
.
Решение.  ;
;  .
.
Так как правая часть уравнения отлична от нуля, то уравнение либо имеет единственное решение, либо не имеет решений.
Если  , то
, то  - единственное решение.
- единственное решение.
Если  , то уравнение
, то уравнение  решений не имеет.
решений не имеет.
Ответ: Если  ,
,  . Если
. Если  , уравнение решений не имеет.
, уравнение решений не имеет.
Задача 6. Найдите значение переменной  , которое не может быть решением уравнения
, которое не может быть решением уравнения  ни при одном значении параметра
ни при одном значении параметра  .
.
Решение.  ;
;  . Данное уравнение можно рассматривать как линейное уравнение относительно переменной
. Данное уравнение можно рассматривать как линейное уравнение относительно переменной  и параметром
и параметром  . Уравнение не будет иметь решение, если
. Уравнение не будет иметь решение, если  , т.е. при
, т.е. при  .
.
Ответ: 0.
Упражнение 3. Решите уравнения.
 3.
3. 
 4.
4. 
Ответы:
Если  , то
, то  ; если
; если  , уравнение решений не имеет.
, уравнение решений не имеет.
Если  , то
, то  ; если
; если  ,
,  - любое действительное число.
- любое действительное число.
Если  , то
, то  ; если
; если  ,
,  - любое действительное число.
- любое действительное число.
Если  , то
, то  ; если
; если  , уравнение решений не имеет.
, уравнение решений не имеет.
Упражнение 4. Решите уравнения.

Ответы: 1) Если , то  . Если
. Если  ,
,  - любое действительное число. Если
- любое действительное число. Если  , уравнение решений не имеет.
, уравнение решений не имеет.
2) Если , то  . Если
. Если  , то
, то - любое действительное число. Если
- любое действительное число. Если  , то уравнение решений не имеет.
, то уравнение решений не имеет.
3) При  уравнение не определено. Если , то
уравнение не определено. Если , то  . Если
. Если  , то
, то  - любое действительное число. Если
- любое действительное число. Если  , то уравнение решений не имеет.
, то уравнение решений не имеет.
4) Если ,  - любое действительное число, то .
- любое действительное число, то .
Если  ,
,  , то
, то  -любое действительное число.
-любое действительное число.
Если  , , то уравнение решений не имеет.
, , то уравнение решений не имеет.
Задача 7 Найдите все значения параметра , при которых уравнение имеет бесконечно много решений.
, при которых уравнение имеет бесконечно много решений.
Решение. Преобразуем данное уравнение следующим образом:
;
; .
Если  , то при всех таких значениях параметра уравнение будет иметь единственное решение, и поэтому такие значения параметра нас не интересуют.
, то при всех таких значениях параметра уравнение будет иметь единственное решение, и поэтому такие значения параметра нас не интересуют.
Пусть  ;
;  ;
;  .
.
Значение параметра  будет удовлетворять условию задачи, если при его подстановке обе части уравнения будут одновременно равны нулю.
будет удовлетворять условию задачи, если при его подстановке обе части уравнения будут одновременно равны нулю.
Если  , то
, то 
Если  , то
, то 
Следовательно, искомое значение параметра  .
.
Ответ:  .
.
Задача 8. Решите уравнение  при всех значениях параметров
при всех значениях параметров  и
и  , таких, что
, таких, что  .
.
Решение. По условию,  , поэтому
, поэтому
; ;  .
.
Ответ: для любых значений параметров  решением уравнения является число, равное 1.
решением уравнения является число, равное 1.
Задача 9. Найдите все значения параметра  , при каждом из которых решение уравнения больше 2.
, при каждом из которых решение уравнения больше 2.
Решение. ; .
Если  , то уравнение решений не имеет, при всех других значениях параметра уравнение будет иметь корень, задаваемых формулой . Таким образом, искомые значения параметра будут являться решением неравенства
, то уравнение решений не имеет, при всех других значениях параметра уравнение будет иметь корень, задаваемых формулой . Таким образом, искомые значения параметра будут являться решением неравенства
; ;  .
.
Ответ:  .
.
Упражнение 5. Найдите значение переменной  , которое не может быть решением уравнения ни при одном значении параметра.
, которое не может быть решением уравнения ни при одном значении параметра.
 3.
3. 
 4.
4. 
Ответы: 1) 0; 2) -4; 3) 0; 4) 1.
Упражнение 6.
Найдите все значения параметра  , при каждом из которых уравнение
, при каждом из которых уравнение  не имеет решений.
не имеет решений.
Ответ: 2.
Найдите все значения параметра  , при каждом из которых уравнение
, при каждом из которых уравнение  не имеет решений.
не имеет решений.
Ответ: -1.
Найдите все значения параметра  , при каждом из которых уравнение
, при каждом из которых уравнение  не имеет решений.
не имеет решений.
Ответ: 0.
Найдите все значения параметра  , при каждом из которых уравнение
, при каждом из которых уравнение  обращается в тождество.
обращается в тождество.
Ответ: 1.
Найдите все значения параметра  , при каждом из которых уравнение
, при каждом из которых уравнение  не имеет решений.
не имеет решений.
Ответ: -1.
Решение линейных неравенств.
Задача 10 . Решите неравенство  .
.
Решение.  ;
;  ;
;  .
.
Если  , то неравенство примет вид
, то неравенство примет вид  и его решением будет являться любое значение переменной
и его решением будет являться любое значение переменной  .
.
Если  , то
, то  ,
, 
Если  , то
, то  ,
,  .
.
Ответ: При  решением является любое значение
решением является любое значение  . При
. При  . При
. При  .
.
Задача 11. Решите неравенство .
Решение. . Умножим обе части неравенства на 6:
; ;
Если  , то неравенство приобретает вид ;
, то неравенство приобретает вид ;  , из чего следует, что решением не может являться ни одно значение переменной
, из чего следует, что решением не может являться ни одно значение переменной  . Таким образом, при
. Таким образом, при  неравенство решений не имеет.
неравенство решений не имеет.
Если  , то , .
, то , .
Если  , то , .
, то , .
Ответ: При  неравенство не имеет решений.. При
неравенство не имеет решений.. При  . При
. При  .
.
Задача 12. Решите неравенство .
Решение. Заметим, что в данном случае параметр  может принимать только значения, отличные от нуля. При
может принимать только значения, отличные от нуля. При  данное неравенство не имеет смысла.
данное неравенство не имеет смысла.
; ; ; ; ;  .
.
Типичная ошибка в данном случае – умножение на  обеих частей неравенства, так как параметр
обеих частей неравенства, так как параметр  может принимать как положительные, так и отрицательные значения.
может принимать как положительные, так и отрицательные значения.
Вспомним определение параметра как «управляющей переменной», что особенно наглядно проявляется при решении неравенств.
Если  , то неравенство имеет вид
, то неравенство имеет вид  , и его решением не может служить ни одно значение переменной
, и его решением не может служить ни одно значение переменной  .
.
Если  , т.е. когда
, т.е. когда  , получим, что
, получим, что  .
.
Если  , т.е.
, т.е.  , то .
, то .
Ответ: При  неравенство решений не имеет. При
неравенство решений не имеет. При  .
.
При  или
или 
Задача 13. Решите неравенство .
Решение. Из условия следует, что параметр  может принимать любые значения, кроме
может принимать любые значения, кроме  . Преобразуем неравенство следующим образом:
. Преобразуем неравенство следующим образом:
; ; ; ; .
Умножение обеих частей неравенства на  приведет к ошибке в решении.
приведет к ошибке в решении.
Если  , то неравенство имеет вид
, то неравенство имеет вид  и обращается в верное числовое неравенство при любом значении переменной
и обращается в верное числовое неравенство при любом значении переменной  .
.
Если  , т.е. если
, т.е. если  , неравенство .
, неравенство .
Если  или
или  , получим, что
, получим, что  и .
и .
Ответ: При  решением неравенства является любое значение переменной
решением неравенства является любое значение переменной  . При
. При  . При
. При  .
.
Системы линейных уравнений с двумя переменными.
Определение. Системой двух линейных уравнений с двумя переменными называется система вида , где  ,
,  ,
,  ,
, 
 ,
,  - действительные числа, причем
- действительные числа, причем  и
и  .
.
Определение. Решением системы двух линейных уравнений с двумя переменными называется упорядоченная пара значений этих переменных, обращающая в верное числовое равенство каждое уравнение системы.
Пусть пара чисел  - решение данной системы. Подставляя эти значения в уравнения системы, получим верные числовые равенства: . Числовое равенство не изменится, если обе его части одновременно умножить на любое, отличное от нуля число или к обеим частям прибавить равные числа
- решение данной системы. Подставляя эти значения в уравнения системы, получим верные числовые равенства: . Числовое равенство не изменится, если обе его части одновременно умножить на любое, отличное от нуля число или к обеим частям прибавить равные числа
Исключая  из первого уравнения, мы приводим систему равенств к виду , из которого следует, что пара чисел
из первого уравнения, мы приводим систему равенств к виду , из которого следует, что пара чисел  является решением системы . Исключая
является решением системы . Исключая  , получим , откуда следует, что та же пара чисел
, получим , откуда следует, что та же пара чисел  - решение системы . Очевидно, что если
- решение системы . Очевидно, что если  - решение одной из получившихся систем, то эта же пара чисел - решение исходной системы. Заметим, что коэффициент при остающейся переменной одинаков. Таким образом, мы приходим к методу Крамера или методу определителей решения систем линейных уравнений.
- решение одной из получившихся систем, то эта же пара чисел - решение исходной системы. Заметим, что коэффициент при остающейся переменной одинаков. Таким образом, мы приходим к методу Крамера или методу определителей решения систем линейных уравнений.
Определение. Определителем системы линейных уравнений называется число, равное  и записываемое в виде
и записываемое в виде .
.
При этом правые части уравнений, содержащих одну оставшуюся переменную, также можно записать в виде определителей:
 ;
;  .
.
Метод Крамера является наиболее удобным для исследования систем линейных уравнений.
Если  , то система имеет единственное решение .
, то система имеет единственное решение .
Эти формулы носят название формул Крамера.
Геометрический смысл единственности решения состоит в том, что прямые, задаваемые уравнениями системы, пересекаются в одной точке.
 . Если при этом
. Если при этом  , то система решений не имеет. Геометрически это означает, что прямые, задаваемые уравнениями системы, параллельны.
, то система решений не имеет. Геометрически это означает, что прямые, задаваемые уравнениями системы, параллельны.
Если  ,то система имеет бесконечное множество решений вида
,то система имеет бесконечное множество решений вида
.
В этом случае оба уравнения системы задают на плоскости одну прямую, координаты точек которой и являются решениями данной системы.
Если коэффициенты системы  ,
,  ,
,  ,
,  не равны нулю, то условие
не равны нулю, то условие 
 .
.
Если при этом  и
и  ,то
,то  ;
;

 .
.
Задача 14. Решите систему уравнений .
Решение.
 ; ; .
; ; .
 . Ответ:
. Ответ: 
Задача 15. Найдите все значения параметра  , при каждом из которых система уравнений имеет единственное решение.
, при каждом из которых система уравнений имеет единственное решение.
Решение. Найдем определитель системы. .
Искомые значения параметра задаются неравенством  .
.
 .
.
Ответ : При система имеет единственное решение.
Задача 16. Найдите все значения параметра  , при каждом из которых система уравнений не имеет решений.
, при каждом из которых система уравнений не имеет решений.
Решение. Найдем определители системы: ; ; .
Система не имеет решения в том случае, если определитель системы равен нулю, а хотя бы один из частных определителей системы отличен от нуля.
Искомые значения параметра задаются системой
Корни уравнения 
 . Подставим полученные значения в систему ;
. Подставим полученные значения в систему ;  . Таким образом, при
. Таким образом, при  система не имеет решений.
система не имеет решений.
Ответ: -4.
Задача 17. Найдите все значения параметра  , при каждом из которых система уравнений имеет бесконечно много решений.
, при каждом из которых система уравнений имеет бесконечно много решений.
Решение. ; ; .
Так как система должна иметь бесконечное множество решений, то искомые значения параметров задаются системой

Ответ: 3.
Упражнение 7. Найдите все значения параметра, при каждом из которых система уравнений не имеет решений.
1) 2)
3)  4)
4)
Ответы: 1) -4; 2)  ; 3) -1; 4) -2
; 3) -1; 4) -2
Упражнение 8. Найдите все значения параметра, при каждом из которых система уравнений имеет бесконечное множество решений.
1) 2)
3) 4)
Ответы: 1) 2; 2) 5; 3) -3; 4) 3.
Упражнение 9. Найдите все значения параметра, при каждом из которых система уравнений имеет единственное решение.
1) 2)
3) 4)
Ответы: 1) ; 2) ;
3) ; 4)  .
.
14







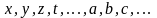

 еализация представленного разделения может отрабатываться в системе упражнений, подобных следующему:
еализация представленного разделения может отрабатываться в системе упражнений, подобных следующему: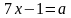 6)
6) 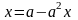
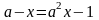 7)
7) 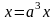
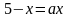 8)
8) 
 9)
9) 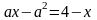
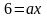 10)
10) 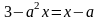
 . Укажите уравнения, содержащие и не содержащие параметры.
. Укажите уравнения, содержащие и не содержащие параметры. 6)
6) 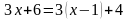
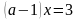 7)
7) 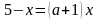
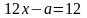 8)
8) 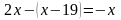
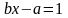 9)
9) 









