Применение метода рационализации для решения неравенств.
Тема «Неравенства» занимает важное место в курсе математики. Объяснить это можно тем, что с помощью неравенств решают многие математические задачи, в том числе – задачи прикладного характера. Поэтому методике решения различных неравенств уделяется особое внимание, отводится достаточно большое количество часов. Но как показывает анализ контрольных, экзаменационных работ, учащиеся средней школы испытывают затруднения при решении неравенств и их систем. Задача №15 ЕГЭ по математике предусматривает умение выпускниками решать различные неравенства. При решении этой задачи выпускник должен показать следующие умения: анализировать задачу, выбирать математическую модель, использовать рациональный метод решения, применять теоретические знания к решению задачи. Последние годы в контрольно-измерительных материалах ЕГЭ представлены логарифмические или показательные неравенства.
Являясь экспертом по оцениванию заданий с развернуым ответом, могу отметить основные ошибки:
- неверное определение области допустимых значений неравенства;
- неумение использовать равносильные преобразования и вычислительные ошибки;
- незнание алгоритма метода интервалов;
- незнание свойств логарифмов, логарифмической и показательной функций.
Поэтому, как учитель, ставлю задачу: спланировать изучение данной темы таким образом, чтобы как можно большее количество моих выпускников приступили к решению задачи №15 и получили за нее максимальный балл. Для этого необходимо расширить набор методов решения неравенств, закрепить навык решения на большом количестве примеров.
Изучив основные методы решения показательных неравенств, переходим к заданиям с параметром.
Решим неравенство: 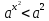 .
.
Решение:
Рассмотрим три случая.
Если 0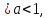 то
то 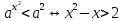
х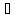 (-
(-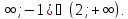
Если а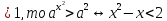
х
Если а=1, то неравенство не имеет решений.
Ответ: при 0 х
х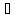 (-
(-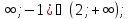
при а=1 нет решений;
при а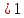 х
х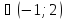 .
.
Учащиеся задают вопрос: « А нельзя ли решить это неравенство другим способом, более кратким, без рассмотрения трех случаев?»
Рассмотрим показательную функцию y= , где h
, где h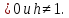
При h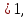 функция возрастает на области определения. Тогда знак выражения
функция возрастает на области определения. Тогда знак выражения 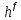 -
-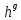 совпадает со знаком выражения f-g.
совпадает со знаком выражения f-g.
При 0 функция убывает на области определения. Тогда знак выражения
функция убывает на области определения. Тогда знак выражения 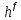 -
-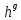 совпадает со знаком выражения(h-1)( f-g).
совпадает со знаком выражения(h-1)( f-g).
Решим данное неравенство, используя полученный выше вывод.
Решить неравенство: 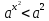 .
.
Решение:
Если а=1, то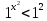 . Решений нет.
. Решений нет.
Если а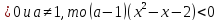
Х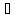 (-
(-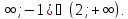
Если а

х
Аналогичным образом можно рассмотреть логарифмическое неравенство. Рассмотрим неравенство, которое приведено к стандартному виду , где символ V можно заменить одним из знаков сравнения:  Знак этого неравенства будет зависеть от множителей, входящих в неравенство. Если какой-либо множитель громоздкий, то его можно заменить другим множителем, равносильным (совпадающим по знаку) в области допустимых значений неравенства. Можно заменить некоторые множители, а можно заменить и все. Важно помнить, что неравенство должно быть представлено множителями, сравнимыми с нулем. Получили метод замены множителей, который еще называют методом рационализации. Метод рационализации позволяет перейти от неравенства, содержащего сложные логарифмические, показательные, иррациональные выражения, выражения с модулями, к равносильному ему более простому рациональному неравенству на области допустимых значений.
Знак этого неравенства будет зависеть от множителей, входящих в неравенство. Если какой-либо множитель громоздкий, то его можно заменить другим множителем, равносильным (совпадающим по знаку) в области допустимых значений неравенства. Можно заменить некоторые множители, а можно заменить и все. Важно помнить, что неравенство должно быть представлено множителями, сравнимыми с нулем. Получили метод замены множителей, который еще называют методом рационализации. Метод рационализации позволяет перейти от неравенства, содержащего сложные логарифмические, показательные, иррациональные выражения, выражения с модулями, к равносильному ему более простому рациональному неравенству на области допустимых значений.
Приемы рационализации:
| 
|  0 0
|
|  1 1
|  0 0
|
|  0 0
|  0 0
|
|  0 0
|  0 0
|
|  
|  0 0
|
| 

| ( 0 0
|
| 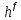 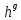
|  0 0
|
| 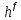 1 1
| 
|
|  
|  *h0 *h0
|
|  
|  0 0
|
|  
|  
|
Где f 0, g 0, h 1,p 0,p
1,p 0,p 
f, g - функции от х
h, p - функция или число
- один из знаков , ,, и обязательно учитываем ОДЗ исходного неравенства.
Рассмотрим примеры решения неравенств с применением метода рационализации.
Решите неравенство: 0
Решение:
Ответ: -7;-6) -5,-1; x=1
Решите неравенство:
Решение:
Ответ: [-2; -1), [3; 4)
Решите неравенство:
Решение:



При  , тогда
, тогда

Ответ: x=-5, -3x 0,5x 1, 3x
1, 3x 7
7
Решите неравенство:
Решение:
Решите неравенство:  1
1
Решение:
ОДЗ: 

 t
t
t 

x+1 
x  -1
-1
x 
Используя метод рационализации, получим:
 x(x-1)0
x(x-1)0
 x
x 0
0
Ещё раз рационализируем:
(2-1)(x+1)x(x-1)0
(x+1)x(x-1)0
Ответ: -1x0; x1
Решите неравенство:
Решение:
Применяя метод замены множителей:
Ответ: [ -36, -2), ( -2; -1), ( - ; 0)
; 0)
Решите неравенство:
Решение:



x=6 удовлетворяет неравенству
1
Пусть
=
Так как
- это знак 
При  исходное неравенство примет вид:
исходное неравенство примет вид:
, где  ;
; 
Используя рационализацию, получим:
Ответ: (- ; -2); (-2; 2-
; -2); (-2; 2- ); [6; +
); [6; +
МГУ(Экономический факультет),2013г
Решите неравенство:
Решение:
Пусть  = t
= t
 0
0
Разложим на множители 2
t = 3 2*27-19*3+3=0 верно
По схеме Горнера
|
| 2 | 0 | -19 | 3 |
|  =3 =3
| 2 | 6 | -1 | 0 |


-  или 3
или 3
-  3
3
1

-2 2
2
Ответ: , 
Решите неравенство:  -8-
-8-

Решение:
 =a
=a
a-8-

a-8
a-8
a-8
a-8 , где a
, где a
Еще раз замена множителей:
0 , x






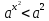 .
.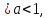 то
то 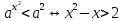
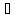 (-
(-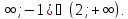
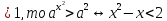

 х
х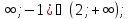
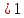 х
х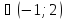 .
. , где h
, где h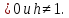
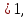 функция возрастает на области определения. Тогда знак выражения
функция возрастает на области определения. Тогда знак выражения 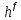 -
-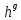 совпадает со знаком выражения f-g.
совпадает со знаком выражения f-g.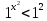 . Решений нет.
. Решений нет.