МЕТОДИЧЕСКАЯ РАЗРАБОТКА
студенческой олимпиады
по учебной дисциплине
«Математика»
для студентов 1 курса
специальностей
34.02.01 Сестринское дело и
31.02.02 Акушерское дело
|
| Разработчик: Киреева Н.В.
|
2023
Пояснительная записка
Методическая разработка предназначена для проведения олимпиады по учебной дисциплине «Математика» (далее – Олимпиада) для обучающихся 1 курса специальностей 34.02.01 Сестринское дело и 31.02.02 Акушерское дело.
Олимпиада по учебной дисциплине «Математика» проводится с целью активизация и повышения качества учебно-познавательной деятельности обучающихся, выявление научного и творческого потенциала обучающихся, повышение интереса к математике.
Предполагается, что при подготовке к участию в Олимпиаде, обучающиеся повторят базовые знания школьной математики, узнают новые интересные научные факты, которые позволят им успешно приступить к изучению новых тем дисциплины Математика.
Методическая разработка включает в себя: пояснительную записку, положение об Олимпиаде, задания для студентов, оценочные ведомости, протокол, список использованных источников, фотоотчёт, приложения.
Положение о проведении
студенческой олимпиады по дисциплине «Математика»
для студентов 1 курса,
специальностей 34.02.01 Сестринское дело, 31.02.02 Акушерское дело.
Общее положения
Настоящее положение определяет правила организации и проведения олимпиады по учебной дисциплине «Математика» (далее – Олимпиада), её организационно-методическое обеспечение, правила участия, определения победителей олимпиады.
Олимпиада проводится в соответствии с планом работы Государственного бюджетного профессионального образовательного учреждения «Ейский медицинский колледж» министерства здравоохранения Краснодарского края на 2023-2024 учебный год.
Организатором Олимпиады является преподаватель математики Киреева Н.В.
Основными целями и задачами Олимпиады являются: создание условий для развития у обучающихся интереса к изучаемой дисциплине, совершенствование профессиональной компетентности, распространение и популяризация знаний молодёжи, содействие профессиональной ориентации обучающихся, создание условий их интеллектуального развития.
Олимпиада проводится по заданиям, составленным на основе образовательных программ среднего профессионального образования.
Олимпиада способствует формированию у обучающихся общих компетенций: ОК 01, ОК 02, ОК 03, ОК 05, ОК 06.
Участники Олимпиады
В Олимпиаде на добровольной основе принимают индивидуальное участие обучающиеся 1 курса отделений «Сестринское дело» и «Акушерское дело». Каждую учебную группу представляют не менее 5 участников Олимпиады.
3. Порядок проведения Олимпиады
3.1. Форма проведения - очная.
3.2. Организатор Олимпиады:
разрабатывает, утверждает условия и требования к проведению Олимпиады, устанавливает сроки проведения Олимпиады;
разрабатывает материалы олимпиадных заданий;
разрабатывает критерии оценивания выполненных заданий;
утверждает список победителей и участников,
утверждает результаты Олимпиады, доводит их до сведения участников Олимпиады.
3.4. Членами жюри являются преподаватели цикловых комиссий общеобразовательных дисциплин и общепрофессиональных дисциплин.
3.5. Жюри Олимпиады:
проверяет и оценивает результаты выполнения олимпиадных заданий;
определяет и предоставляет для утверждения список победителей и участников Олимпиады.
4. Сроки и место проведения
4.1. Проведение Олимпиады планируется (дата) в (время) в аудитории (место). На выполнение заданий участникам отводится 1 час.
5. Критерии оценки выполнения заданий олимпиады
5.1. Олимпиада предусматривает выполнение задания, состоящего из 2 частей, первая часть состоит из 10 заданий, вторая часть – из 5. В 1 части каждое верно решённое задание оценивается в 1 балл, во 2 части каждое верно решённое задание оценивается в 2 балла. Во 2 части задания Олимпиады ответы без решения не принимаются!
5.2. Победители выявляются по результатам проверки выполненных заданий и количества набранных баллов.
5.3. Максимальное количество баллов составляет - 20.
6. Подведение итогов Олимпиады
6.1. Победителями Олимпиады признаются участники, набравшие по итогам определённое количество баллов.
6.2. Участники награждаются дипломами согласно следующим результатам:
набравшие 18-20 баллов - Диплом победителя I степени;
набравшие 16-17 баллов - Диплом победителя II степени;
набравшие 14-15 баллов - Диплом победителя III степени.
Набравшие менее14 баллов – сертификат участника Олимпиады.
7. Требования к оформлению
7.1. Верные варианты ответов на 1 часть заданий Олимпиады отмечаются в бланке с заданием путём обведения в кружок правильного варианта ответа, решения и ответы 2 части задания олимпиады оформляются на отдельном бланке. В каждом бланке указывается фамилия, имя, отчество участника, номер группы участника олимпиады.
Ответственный за проведение Олимпиады ФИО
Приложение 1
Часть 1. Тестовые задания для студенческой олимпиады
по учебной дисциплине «Математика»
Инструкция по выполнению
Вам представлено 10 тестовых заданий, правильно выполненное задание оценивается в 1 балл. Максимальное количество баллов – 10.
Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов. Внимательно прочитайте каждое задание и проанализируйте все варианты возможного решения.
ФИО участника________________________________номер группы____________
| Вопрос 1: Найдите значение функции 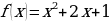 при х= -2 при х= -2 Варианты ответов: |
| Вопрос 2: Две стороны четырёхугольника равны 1 и 7. Одна из диагоналей, длина которой равна 3, делит его на два равнобедренных треугольника. Чему равен периметр этого четырёхугольника? Варианты ответов: |
| Вопрос 3: Сколько копеек в децисантикилорубле? Варианты ответов: |
| Вопрос 4: Чему равен угол ABC равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной CD углы, равные 20° и 100° соответственно. 
Варианты ответов: |
| Вопрос 5: Зная длину своего шага, человек может приближенно подсчитать пройденное им расстояние s по формуле s = nl, где n — число шагов, l — длина шага. Какое расстояние прошел человек, если l = 80 см, n = 1600? Ответ выразите в километрах.
Варианты ответов: |
| Вопрос 6: Чему равно значение выражения 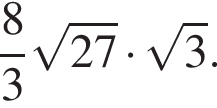
Варианты ответов: |
| Вопрос 7: Смешали некоторое количество 21-процентного раствора некоторого вещества с таким же количеством 95-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора? Варианты ответов: |
| Вопрос 8: В ходе биологического эксперимента в чашку Петри с питательной средой поместили колонию микроорганизмов массой 13мг. За каждые 30 минут масса колонии увеличивается в 3 раза. Найдите массу колонии микроорганизмов через 90 минут после начала эксперимента. Ответ дайте в миллиграммах.
Варианты ответов: |
| Вопрос 9: Найдите десятичную дробь, равную сумме
Варианты ответов: |
| Вопрос 10: Какие из следующих утверждений верны? 1) Если угол равен 45°, то вертикальный с ним угол равен 45°. 2) Любые две прямые имеют ровно одну общую точку. 3) Через любые три точки проходит ровно одна прямая. 4) Если расстояние от точки до прямой меньше 1, то и длина любой наклонной, проведенной из данной точки к прямой, меньше 1.
Варианты ответов: |
Часть 2. Задания для студенческой олимпиады
по учебной дисциплине «Математика»
Инструкция по выполнению
Вам представлено 5 заданий, правильно выполненное задание оценивается в 2 балла. Максимальное количество баллов – 10.
Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов. Внимательно прочитайте каждое задание, выполните его, и запишите решение в специальный бланк.
Задание 1. В книге Елены Молоховец «Подарок молодым хозяйкам» имеется рецепт пирога с черносливом. Для пирога на 10 человек следует взять 1/10 фунта чернослива. Сколько граммов чернослива следует взять для пирога, рассчитанного на 3 человек? Считайте, что 1 фунт равен 0,4 кг.
Задание 2.План местности разбит на клетки. Каждая клетка обозначает квадрат 1м × 1м.
Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных метрах.
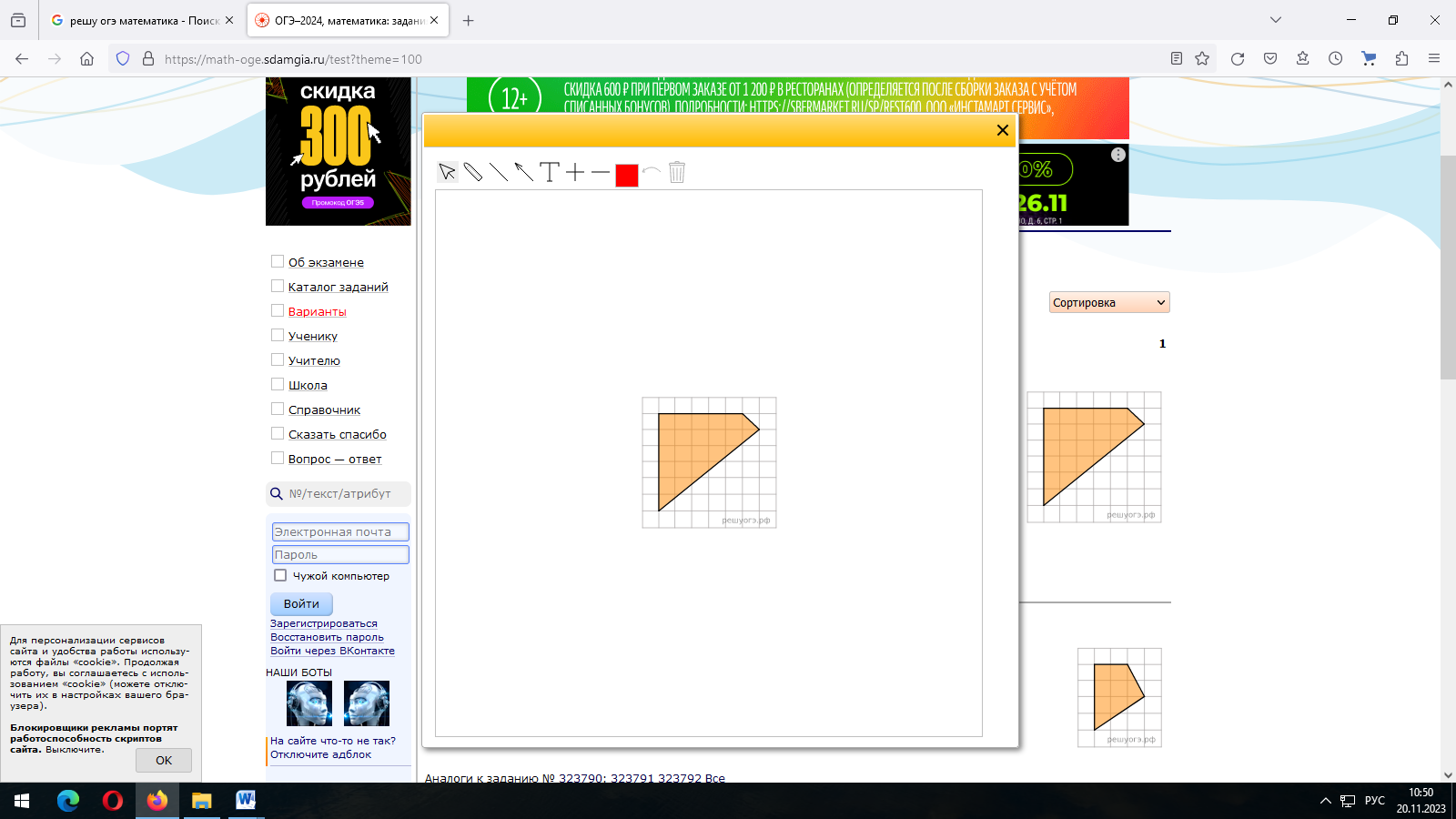
З
адание 3. Колесо имеет 25 спиц. Найдите величину угла (в градусах), который образуют две соседние спицы.
Задание 4. В таблице приведены данные о шести чемоданах.
| Номер чемодана | Длина, см | Высота, см | Ширина, см | Масса, кг |
| 1 | 105 | 54 | 42 | 25 |
| 2 | 78 | 68 | 56 | 24 |
| 3 | 98 | 67 | 45 | 25,5 |
| 4 | 83 | 62 | 50 | 21 |
| 5 | 94 | 69 | 45 | 22 |
| 6 | 101 | 59 | 42 | 19 |
По правилам авиакомпании сумма трёх измерений (длина, высота, ширина) чемодана, сдаваемого в багаж, не должна превышать 203 см, а масса не должна быть больше 23 кг. Какие чемоданы можно сдать в багаж по правилам этой авиакомпании? В ответе укажите номера всех выбранных чемоданов без пробелов, запятых и других дополнительных символов.
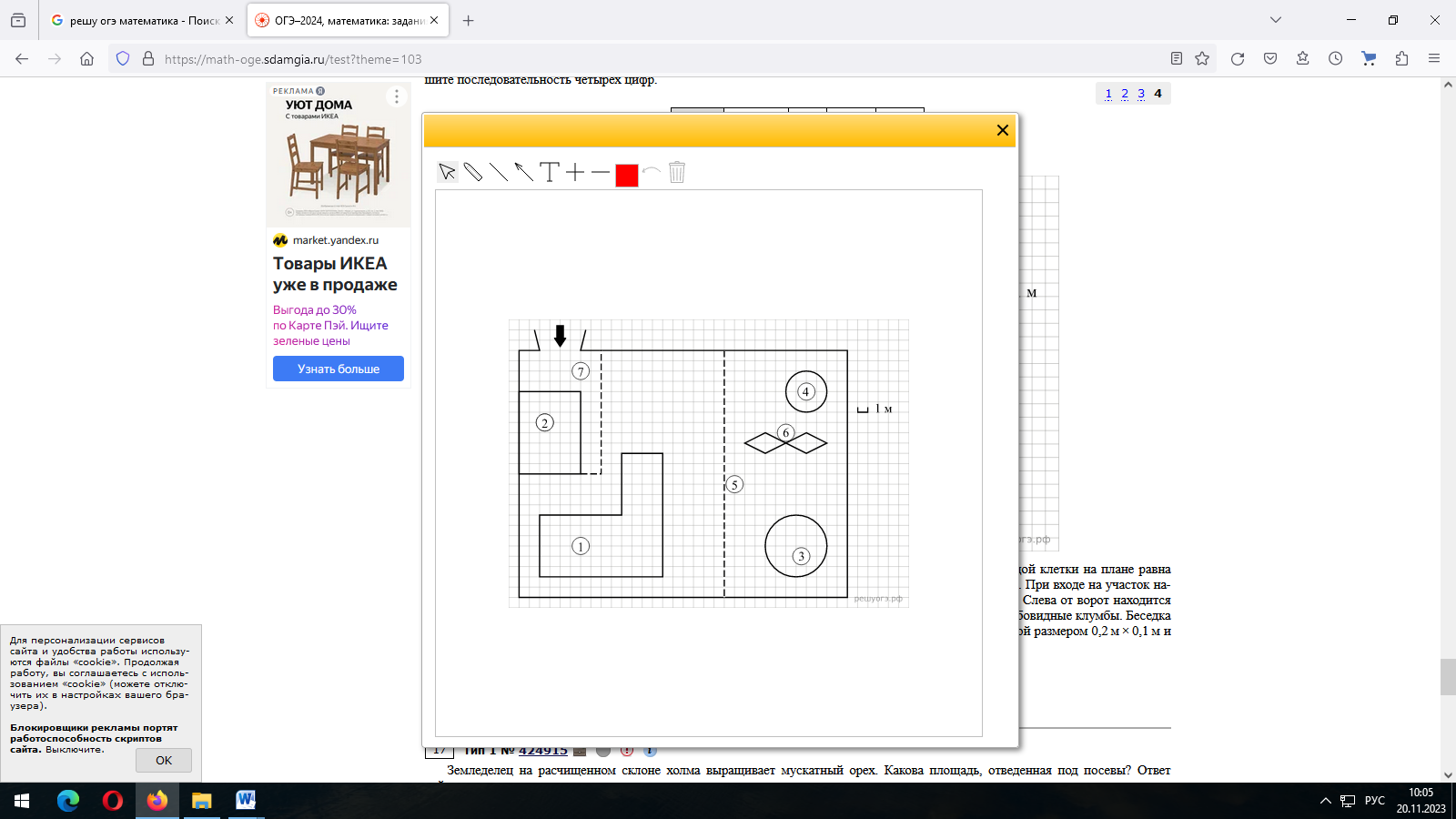
Задание 5. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в ответ запишите последовательность четырех цифр.
| объекты | жилой дом | гараж | бассейн | клумбы |
| цифры |
|
|
|
|
На плане изображено домохозяйство по адресу с. Сергеево, 8-й Кленовый пер, д. 1 (сторона каждой клетки на плане равна 1 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота. При входе на участок напротив ворот находится гараж, а за гаражом — жилой дом. Площадь, занятая гаражом, равна 48 кв. м. Слева от ворот находится большой газон, отмеченный на плане цифрой 5. На газоне имеются круглый бассейн, беседка и две ромбовидные клумбы. Беседка отмечена на плане цифрой 4. При въезде на участок имеется площадка, вымощенная тротуарной плиткой размером 0,2 м × 0,1 м и обозначенная на плане цифрой 7.
Приложение 2
Эталон ответов на часть 1. Тестовые задания для студенческой олимпиады
по учебной дисциплине «Математика»
| № вопроса | Текст вопроса | Правильный ответ |
| Вопрос 1: | Найдите значение функции 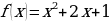 при х= -2 при х= -2 | 1 |
| Вопрос 2: | Две стороны четырёхугольника равны 1 и 7. Одна из диагоналей, длина которой равна 3, делит его на два равнобедренных треугольника. Чему равен периметр этого четырёхугольника? | 18 |
| Вопрос 3: | Сколько копеек в децисантикилорубле? | 100 |
| Вопрос 4: | Чему равен угол ABC равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной CD углы, равные 20° и 100° соответственно. 
| 40° |
| Вопрос 5: | Зная длину своего шага, человек может приближенно подсчитать пройденное им расстояние s по формуле s = nl, где n — число шагов, l — длина шага. Какое расстояние прошел человек, если l = 80 см, n = 1600? Ответ выразите в километрах. | 1,28 |
| Вопрос 6: | Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в ответ запишите последовательность четырех цифр. На плане изображено домохозяйство по адресу с. Сергеево, 8-й Кленовый пер, д. 1 (сторона каждой клетки на плане равна 1 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота. При входе на участок напротив ворот находится гараж, а за гаражом — жилой дом. Площадь, занятая гаражом, равна 48 кв. м. Слева от ворот находится большой газон, отмеченный на плане цифрой 5. На газоне имеются круглый бассейн, беседка и две ромбовидные клумбы. Беседка отмечена на плане цифрой 4. При въезде на участок имеется площадка, вымощенная тротуарной плиткой размером 0,2 м × 0,1 м и обозначенная на плане цифрой 7. 
| объекты | жилой дом | гараж | бассейн | клумбы | | цифры |
|
|
|
|
| 1236 |
| Вопрос 7: | Смешали некоторое количество 21-процентного раствора некоторого вещества с таким же количеством 95-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора? | 58 % |
| Вопрос 8: | В ходе биологического эксперимента в чашку Петри с питательной средой поместили колонию микроорганизмов массой 13мг. За каждые 30 минут масса колонии увеличивается в 3 раза. Найдите массу колонии микроорганизмов через 90 минут после начала эксперимента. Ответ дайте в миллиграммах. | 155 |
| Вопрос 9: | Найдите десятичную дробь, равную сумме | 0,3105 |
| Вопрос 10: | Какие из следующих утверждений верны? 1) Если угол равен 45°, то вертикальный с ним угол равен 45°. 2) Любые две прямые имеют ровно одну общую точку. 3) Через любые три точки проходит ровно одна прямая. 4) Если расстояние от точки до прямой меньше 1, то и длина любой наклонной, проведенной из данной точки к прямой, меньше 1. | 1 |
Эталоны ответов на часть 2. Задания для студенческой олимпиады
по учебной дисциплине «Математика»
Задание 1. В книге Елены Молоховец «Подарок молодым хозяйкам» имеется рецепт пирога с черносливом. Для пирога на 10 человек следует взять 1/10 фунта чернослива. Сколько граммов чернослива следует взять для пирога, рассчитанного на 3 человек? Считайте, что 1 фунт равен 0,4 кг.
Решение. Поскольку на 10 человек следует взять 0,1 фунта чернослива, на одного человека следует взять 0,01 фунта чернослива. Тогда на трех человек потребуется 0,03 фунта чернослива, что составляет 0,03 · 0,4 = 0,012 кг или 12 граммов.
Ответ: 12.
Задание 2.План местности разбит на клетки. Каждая клетка обозначает квадрат 1м × 1м.
Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных метрах.

Решение.
Найдем площадь данной фигуры по формуле Пика:
S = В + Г/2 − 1,
где В — число узлов сетки внутри фигуры, Г — число узлов сетки на границе фигуры, включая вершины. Получаем:
S = 15 + 13/2 − 1 = 20,5.
Ответ: 20,5.
Второй вариант решения.
Площадь данной фигуры равна разности площади квадрата и двух треугольников:
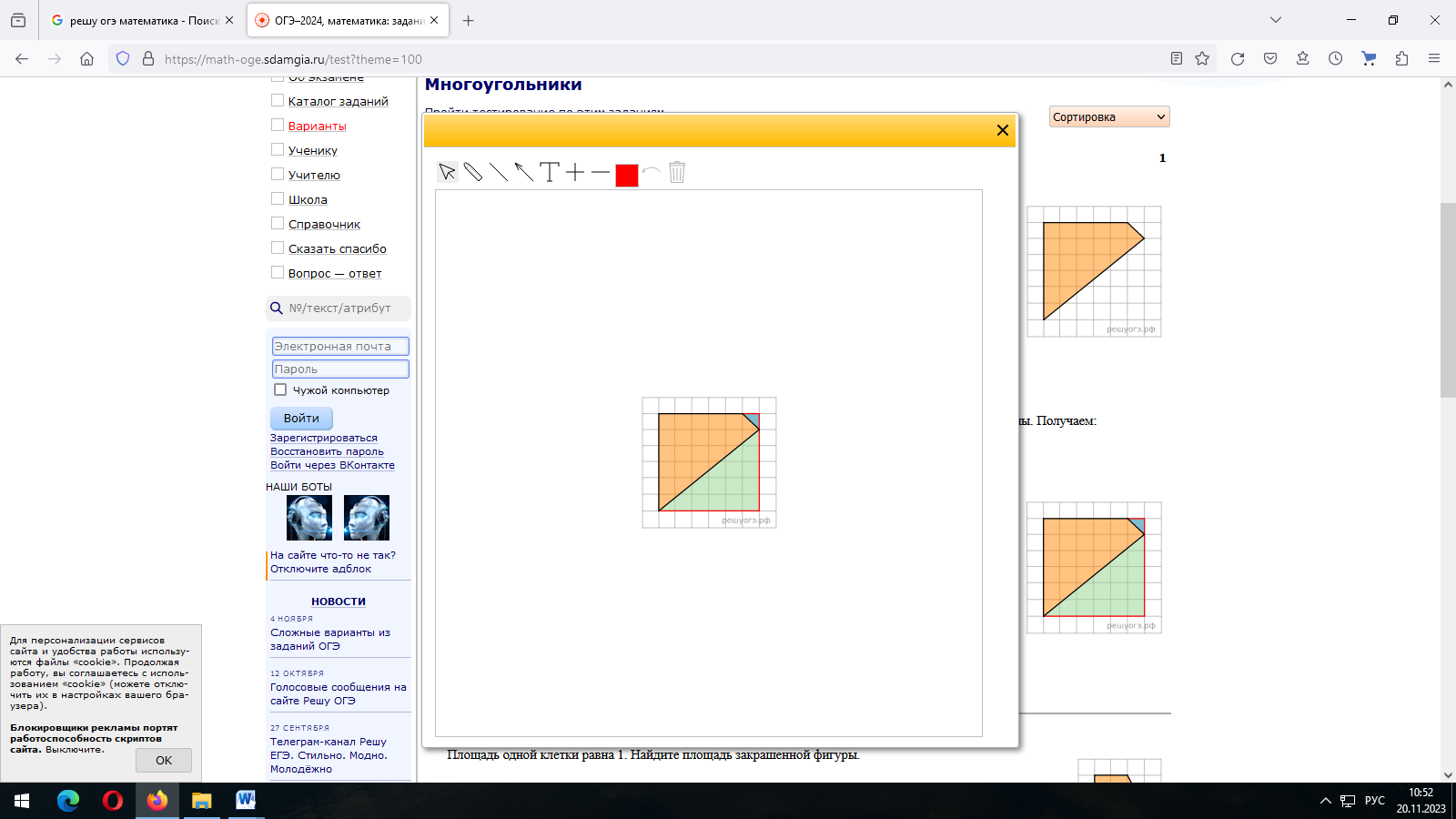
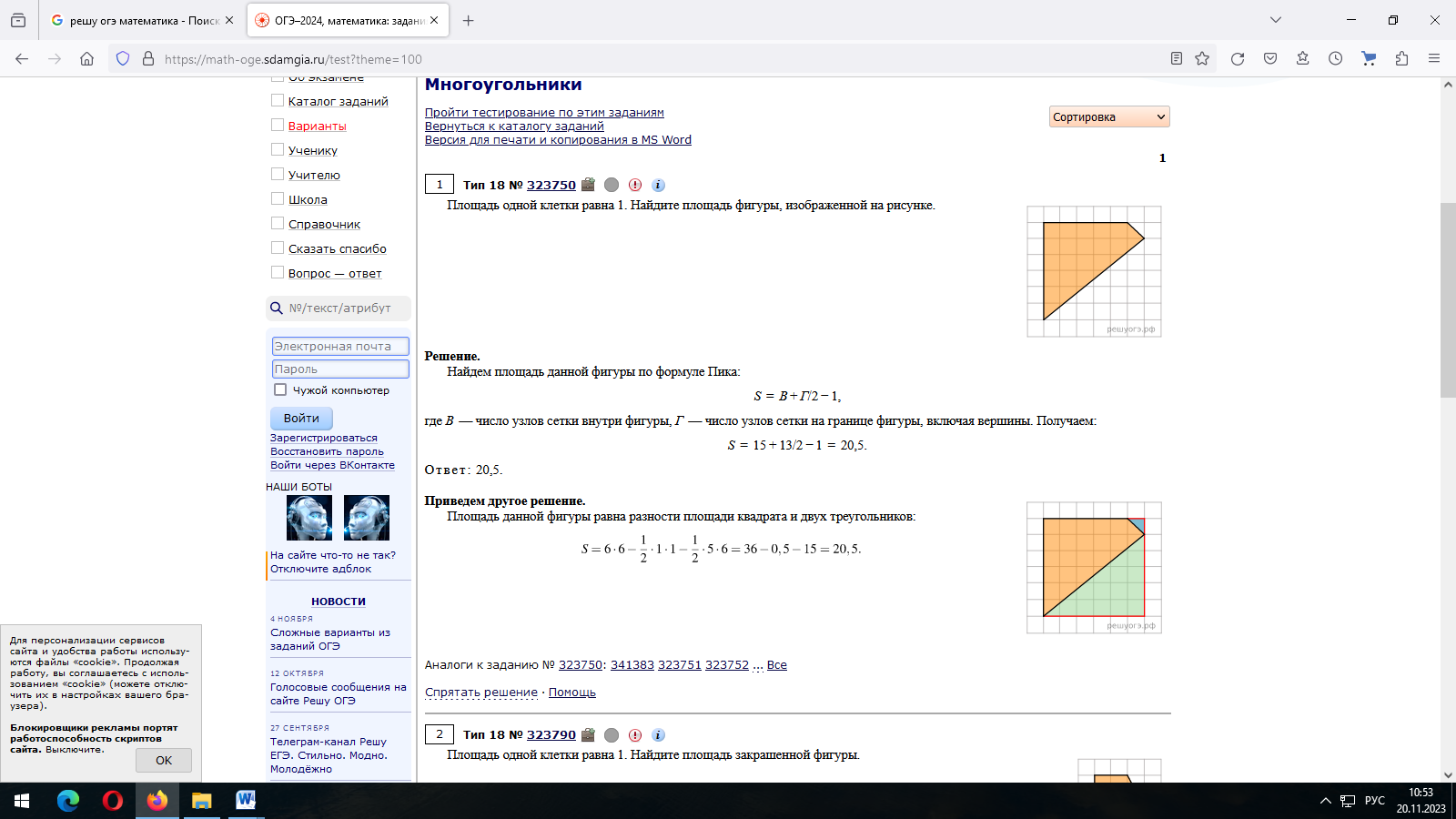
Ответ: 20,5.
З
адание 3. Колесо имеет 25 спиц. Найдите величину угла (в градусах), который образуют две соседние спицы.
Решение. Спицы делят колесо на двадцать пять равных секторов, а значит, делят полный угол 360° на 25 равных углов по 14,4° каждый.
Ответ: 14,4.
Задание 4. В таблице приведены данные о шести чемоданах.
| Номер чемодана | Длина, см | Высота, см | Ширина, см | Масса, кг |
| 1 | 105 | 54 | 42 | 25 |
| 2 | 78 | 68 | 56 | 24 |
| 3 | 98 | 67 | 45 | 25,5 |
| 4 | 83 | 62 | 50 | 21 |
| 5 | 94 | 69 | 45 | 22 |
| 6 | 101 | 59 | 42 | 19 |
По правилам авиакомпании сумма трёх измерений (длина, высота, ширина) чемодана, сдаваемого в багаж, не должна превышать 203 см, а масса не должна быть больше 23 кг. Какие чемоданы можно сдать в багаж по правилам этой авиакомпании? В ответе укажите номера всех выбранных чемоданов без пробелов, запятых и других дополнительных символов.
Решение. Масса первого чемодана превышает норму провоза.
Масса второго чемодана превышает норму провоза.
Масса третьего чемодана превышает норму провоза.
Сумма трех измерений для четвертого чемодана соответствует требованием компании.
Сумма трех измерений для пятого чемодана не соответствует требованием компании.
Сумма трех измерений для шестого чемодана соответствует требованием компании.
Ответ: 46.
Задание 5. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в ответ запишите последовательность четырех цифр.
| объекты | жилой дом | гараж | бассейн | клумбы |
| цифры |
|
|
|
|
На плане изображено домохозяйство по адресу с. Сергеево, 8-й Кленовый пер, д. 1 (сторона каждой клетки на плане равна 1 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота. При входе на участок напротив ворот находится гараж, а за гаражом — жилой дом. Площадь, занятая гаражом, равна 48 кв. м. Слева от ворот находится большой газон, отмеченный на плане цифрой 5. На газоне имеются круглый бассейн, беседка и две ромбовидные клумбы. Беседка отмечена на плане цифрой 4. При въезде на участок имеется площадка, вымощенная тротуарной плиткой размером 0,2 м × 0,1 м и обозначенная на плане цифрой 7.

Решение.
При входе на участок напротив ворот находится гараж, а за гаражом — жилой дом. Значит, гараж отмечен цифрой 2, а жилой дом — цифрой 1. Слева от ворот находится большой газон, отмеченный на плане цифрой 5. На газоне имеются круглый бассейн, беседка и две ромбовидные клумбы. Беседка отмечена на плане цифрой 4. Следовательно, бассейн отмечен цифрой 3, а клумбы — цифрой 6.
Ответ: 1236.
Приложение 3
Бланк ответов на часть 2. Задания студенческой олимпиады
по учебной дисциплине «Математика»
ФИО участника_________________________________группа____________
Допустимо заполнять бланк ответов не печатными буквами, а своим обычным почерком, аккуратно и разборчиво, не выходя за границы.
| № задания | решение | ответ |
| Задание 1 |
|
|
| Задание 2 |
|
|
| Задание 3 |
|
|
| Задание 4 |
|
|
| Задание 5 |
|
|
Приложение 4
протокол студенческой олимпиады
по учебной дисциплине «Математика»
Дата:_______________________
Оцениваемые компетенции:
- овладение общими компетенциями: ОК 01, ОК 02, ОК 03, ОК 05, ОК 06.
Специальность: 34.02.01 Сестринское дело, 31.02.02 Акушерское дело.
| № | ФИО студента | Группа | Количество баллов | Результат участия |
| 1 |
|
|
|
|
| 2 |
|
|
|
|
| 3 |
|
|
|
|
| 4 |
|
|
|
|
| 5 |
|
|
|
|
| 6 |
|
|
|
|
| 7 |
|
|
|
|
| 8 |
|
|
|
|
| 9 |
|
|
|
|
| 10 |
|
|
|
|
| 11 |
|
|
|
|
| 12 |
|
|
|
|
| 13 |
|
|
|
|
| 14 |
|
|
|
|
| 15 |
|
|
|
|
| 16 |
|
|
|
|
| 17 |
|
|
|
|
| 18 |
|
|
|
|
| 19 |
|
|
|
|
| 20 |
|
|
|
|
Жюри:
__________________ФИО;
__________________ФИО
Приложение 5
Список участников студенческой олимпиады
по учебной дисциплине «Математика»







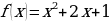 при х= -2
при х= -2















