Департамент охраны здоровья населения Кемеровской области
Государственного бюджетного профессионального образовательного учреждения
«Кемеровский областной медицинский колледж»
Новокузнецкий филиал
Методическая разработка теоретического занятия
Дисциплины «Математика»
Раздел I. Связь математики с медициной
Для специальности 34.02.01 Сестринское дело
Занятие № 6
Раздел 3. Теория вероятности. Тема 3.1. Основные понятия теории вероятности
Составлена преподавателем
Шилепиной Н. И.
2018
Рассмотрен на заседании МОП
гуманитарных и социально – экономических дисциплин
Протокол № _________________________
от __________________________________
Председатель
________________________ Е. В. Златкус
Утвержден на методическом совете
Протокол № _________________________
от __________________________________
Председатель
______________________ Н.Б. Красина
Составитель: Н. И. Шилепина, преподаватель математики
Обучающая цель:
Студент должен знать: основные понятия и методы теории вероятностей и математической статистики.
Студент должен уметь: решать прикладные задачи в области профессиональной деятельности.
Развивающая цель:
ОК 8. Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать и осуществлять повышение квалификации.
Воспитательная цель:
ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.
ОК 9. Ориентироваться в условиях смены технологий в профессиональной деятельности.
Тип занятия: изучения нового материала
Вид занятия: теоритическое
Оснащение занятия:
Литература:
Основная литература:
1. Омельченко, В. П. Математика: компьютерные технологии в медицине [Текст]: учебн. для студентов / В. П. Омельченко, А. А. Демидова. – Ростов н/Д. : Феникс, 2012. – 588 с.
Дополнительная литература:
1. Пехлецкий И. Д. Математика. – М. : Мастерство, 2001. – 367 с.
2. Лисичкин В. Т., Соловейчик И. Л. Математика. – М. : Высшая школа, 1991. – 480 с.
3. Баврин И. И. Высшая математика : учебник для студентов. – М. : Высшая школа, 2000. – 544 с.
Структура занятия
1. Организационный момент
2. Постановка целей и задач занятия
3. Мотивация
4. Изложение нового материала
5. Закрепление нового материала
6. Подведение итогов занятия
7. Домашнее задание
Ход занятия
| № п/п | Элементы занятия, учебные вопросы | (мин) примерное | Методы и приемы обучения |
| 1.
| Организационный момент | 4 |
|
| 1.1. Приветствие обучающихся. 1.2. Проверка отсутствующих: | организации и осуществления учебно-познавательной деятельности, вступительное слово |
| 1.3. Освещение плана занятия Тема нашего занятия «Основные понятия теории вероятностей».
|
|
| 2. | Постановка структуры, целей и задач занятия Обучающая цель: Студент должен знать: основные понятия и методы теории вероятностей и математической статистики. Студент должен уметь: решать прикладные задачи в области профессиональной деятельности. Развивающая цель: ОК 8. Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать и осуществлять повышение квалификации. Воспитательная цель: ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес. ОК 9. Ориентироваться в условиях смены технологий в профессиональной деятельности. | 2 | методы организации и осуществления учебно-познавательной деятельности, сообщающее слово |
| 3. | Мотивация - «В жизни мы часто сталкиваемся со случайными явлениями. Чем обусловлена их случайность – нашим незнанием истинных причин происходящего или случайность лежит в основе многих явлений? Споры на эту тему не утихают в самых разных областях науки. Случайным ли образом возникают мутации, насколько зависит историческое развитие от отдельной личности, можно ли считать Вселенную случайным отклонением от законов сохранения? В дальнейшем мы не будем касаться природы понятия случайности, но при каждом конкретном применении теории вероятностей нужно сначала внимательно проанализировать суть происходящих явлений. Попробуем ознакомиться с основными закономерностями случайных процессов.» | 5 | методы стимулирования и мотивации учебной деятельности, сообщающее слово |
| 4. | Изложение нового материала (приложение 1) 4.1. Понятие случайного события. 4.2. Определение вероятности события. 4.3. Основные теоремы и формулы теории вероятности. | 67 | Словесный метод |
| 5. | Физкультминутка (Приложение 2) | 5 | Здоровьесберегающие технологии |
| 6. | Подведение итогов занятия Поблагодарить группу за хорошую работу на занятии. | 5 | методы организации и осуществления учебно-познавательной деятельности, заключительное слово |
| 7. | Домашнее задание 1. Конспект лекции; 2.Работа с учебником: Омельченко, В. П. Математика: компьютерные технологии в медицине [Текст] :учебн. для студентов / В. П. Омельченко, А. А. Демидова. – Ростов н/Д. : Феникс, 2012. – 588 с. | 2 | методы организации и осуществления учебно-познавательной деятельности, сообщающее слово |
Приложение 1
Тема: Основные понятия теории вероятности
Понятие случайного события
История развития.
Первые работы, в которых зарождались основные понятия теории вероятностей, представляли собой попытки создания теории азартных игр (Кардано, Гюйгенс, Паскаль, Ферма и другие в XVI-XVII вв.).
Следующий этап развития теории вероятностей связан с именем Якоба Бернулли (1654 - 1705). Доказанная им теорема, получившая в последствии название «Закона больших чисел», была первым теоретическим обоснованием накопленных ранее фактов.
Дальнейшими успехами теория вероятностей обязана Муавру, Лапласу, Гауссу, Пуассону и др.
Новые наиболее плодотворные периоды связаны с именем П. Л. Чебышева (1821 - 1894) и его учеников.
Невозможные достоверные и случайные события.
Под событием в теории вероятностей понимают любой факт, который может произойти или не произойти в результате опыта со случайным исходом. Самый простой результат такого опыта (например, появление «орла» или «решки» при бросании монеты, попадание в цель при стрельбе, появление туза при вынимании карты из колоды, случайное выпадение числа при бросании игральной кости и т.д.) называется элементарным событием.
Множество всех элементарных событий Е называется пространством элементарных событий.
Например. При бросании игральной кости это пространство состоит из шести элементарных событий, а при вынимании карты из колоды – из 52.
Событие может состоять из одного или нескольких элементарных событий, например, появление двух тузов подряд при вынимании карты из колоды, или выпадение одного и того же числа при трёхкратном бросании игральной кости. Тогда можно определить событие как произвольное подмножество пространства элементарных событий.
Основным понятием теории вероятностей является понятие случайного события. Случайным называется событие, которое в результате данного испытания оно может произойти или не произойти (т.е. результат события нельзя прогнозировать).
Например. Попадание в цель при выстреле из орудия.
Достоверным событием называется всё пространство элементарных событий. Таким образом, достоверное событие – это событие, которое обязательно должно произойти в результате данного опыта.
Например. При бросании игральной кости таким событием является её падение на одну из граней.
Невозможным событием называется пустое подмножество пространства элементарных событий. То есть, невозможное событие не может произойти в результате данного опыта.
Например. Так, при бросании игральной кости невозможным событием является её падение на ребро.
Совместные и несовместные события.
События А и В называются несовместными ( А В = ), если их одновременное появление невозможно.
Например, выпадение и "решки", и "орла" при бросании монеты.
События A и B называются совместными, если появление одного из них не исключает возможности появления другого.
Например, при бросании игральной кости появление двух очков и появление четного числа очков совместны.
Событие называется противоположным событию А, если не произошло событие А.
Например, промах и попадание при стрельбе – противоположные события.
Если при проведении опыта могут произойти несколько событий и каждое из них по объективным условиям не является более возможным, чем другое, то такие события называются равновозможными.
Например, появление двойки, туза и валета при вынимании карты из колоды, выпадение любого из чисел от 1 до 6 при бросании игральной кости и т.п.
События А и В называются тождественными ( А = В ), если событие А происходит тогда и только тогда, когда происходит событие В .
Говорят, что событие А влечёт за собой событие В ( А В ), если из условия "произошло событие А" следует "произошло событие В".
Операции над событиями.
Событие С называется суммой событий А и В ( С = А+В ), если событие С происходит тогда и только тогда, когда происходит либо А , либо В.
Событие С называется произведением событий А и В ( С = А В ), если событие С происходит тогда и только тогда, когда происходит и А , и В.
Событие С называется разностью событий А и В ( С = А – В ), если событие С происходит тогда и только тогда, когда происходит событие А , и не происходит событие В.
Определение вероятности события
Вероятностью события A называют отношение числа m благоприятствующих этому событию исходов к общему числу n всех равновозможных несовместных элементарных исходов, образующих полную группу  .
.
Основные свойства вероятности случайного события
Свойство 1. Вероятность достоверного события равна единице.
Действительно, поскольку каждое событие пространства элементарных исходов удовлетворяет достоверному событию, то получим  .
.
Свойство 2. Вероятность невозможного события равна нулю.
Поскольку число благоприятных невозможному событию исходов равно 0, то получим  .
.
Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.
Итак, вероятность любого события удовлетворяет двойному неравенству:

Пример. В урне 10 пронумерованных шаров с номерами от 1 до 10. Вынули один шар. Какова вероятность того, что номер вынутого шара не превосходит 10?
Решение. Пусть событие А = (Номер вынутого шара не превосходит 10). Число случаев благоприятствующих появлению события А равно числу всех возможных случаев m=n=10. Следовательно, Р(А) =1. Событие А достоверное.
Основные теоремы и формулы теории вероятностей
Теорема о произведении вероятностей
Пусть, например, одновременно бросают два кубика. Количество очков, выпавших на кубиках, можно считать независимыми событиями. Поэтому вероятность того, что на обоих кубиках выпадет 6 очков, равна  .
.
Вероятность произведения двух зависимых событий A и B равна произведению вероятности одного из них на условную вероятность другого, найденную в предположении, что первое событие уже наступило: P(A·B)=P(A)·P(B|A).
Пример: пары событий, для которых выполняется формула P(A·B)=P(A)·P(B|A), но не выполняется формула P(A·B)=P(A)·P(B). Для любого дня в октябре вероятность того, что в Лондоне идет дождь, равна 0,3. При этом если в какой-то день шел дождь, то вероятность того, что на следующий день пойдет дождь, равна 0,7. Найдем вероятность того, что и 1-го и 2-го октября следующего года в Лондоне будет идти дождь: она равна P(A·B)=P(A)·P(B|A)=0,3·0,7=0,21. В последнем равенстве события A и B соответственно означают, что 1-го и 2-го октября следующего года будет идти дождь.
Легко видеть, что если вычислять вероятность по формуле P(A·B)=P(A)·P(B), то мы получим заниженную оценку: 0,09. Это связано с тем, что события A и B — зависимые, поскольку вероятность дождя 2-го октября зависит от того, был ли дождь 1-го октября.
Теорема о сумме вероятностей
Пример: вероятность того, что на кубике выпало число очков, кратное трем равно сумме вероятностей того, что на кубике выпало 3 очка и 6 очков.
Пример: пусть событие A состоит в том, что число очков на кубике кратно 3, а B в том, что оно кратно двум. Событие A состоит из двух результатов, а B — из трех: A=3,6, B=2,4,6. Сумма событий A+B состоит из четырех результатов: 2,3,4,6, а пересечение — из одного результата: A·B=6. Тогда последнее равенство выполняется:
P(A+B)=  =P(A)+P(B)−P(A·B).
=P(A)+P(B)−P(A·B).
Формула полной вероятности
Если B1, B2,…, — несовместные события и в сумме дают достоверное событие, то вероятность события A можно вычислить, зная вероятности событий B1, B2,…,
— несовместные события и в сумме дают достоверное событие, то вероятность события A можно вычислить, зная вероятности событий B1, B2,…, , а также условные вероятности этого события в предположении событий B1, B2,…,
, а также условные вероятности этого события в предположении событий B1, B2,…,  . Выполняется следующая формула:
. Выполняется следующая формула:
P(A)=P(A|B1)·P(B1)+P(A|B2)·P(B2)+…+P(A| )·P(
)·P( ).
).
Пример: во время испытания смешали шарики из двух ваз и вытащили случайный шарик.
Рассмотрим события:
A: шарик белого цвета,
B1: шарик из первой вазы,
B2: шарик из второй вазы.
Поскольку доля белых шариков в первой вазе равна
 , а во второй вазе равна
, а во второй вазе равна  , то условные вероятности равны P(A|B1) =
, то условные вероятности равны P(A|B1) = и P(A|B2) =
и P(A|B2) =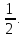
В первой вазе 24 шарика, а во второй — 12 шариков. Поэтому вероятности событий B1 и B2: P(B1) =  , P(B2)=
, P(B2)= .
.
Тогда вероятность вытащить белый шарик:
P(A)=P(A|B1)·P(B1)+P(A|B2)·P(B2) =  .
.
Можно проверить результат: всего в двух вазах 36 шариков, из них 14 белых. Поэтому P(A) =  .
.







 .
. .
. .
.
 .
. =P(A)+P(B)−P(A·B).
=P(A)+P(B)−P(A·B). — несовместные события и в сумме дают достоверное событие, то вероятность события A можно вычислить, зная вероятности событий B1, B2,…,
— несовместные события и в сумме дают достоверное событие, то вероятность события A можно вычислить, зная вероятности событий B1, B2,…, , а во второй вазе равна
, а во второй вазе равна  , то условные вероятности равны P(A|B1) =
, то условные вероятности равны P(A|B1) =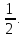
 , P(B2)=
, P(B2)= .
. .
.









