| Билет 1. Сформулируйте и докажите теорему, выражающую второй признак равенства треугольников. Какой отрезок называется высотой треугольника? Сколько высот имеет треугольник? Сформулируйте теорему о медиане равнобедренного треугольника. Задача на оценку «3» Треугольники АВС и KLM равны. Известно, что угол АВС равен углу KLM, угол ВСА равен углу LMK, АВ = 9 см, АС = 12 см. Чему равны соответствующие стороны треугольника KLM? Задача на оценку «4» На рисунке отрезок ВО является биссектрисой угла АВС. АВ=ВС. Найдите отрезок DC, если отрезок DA=5 см 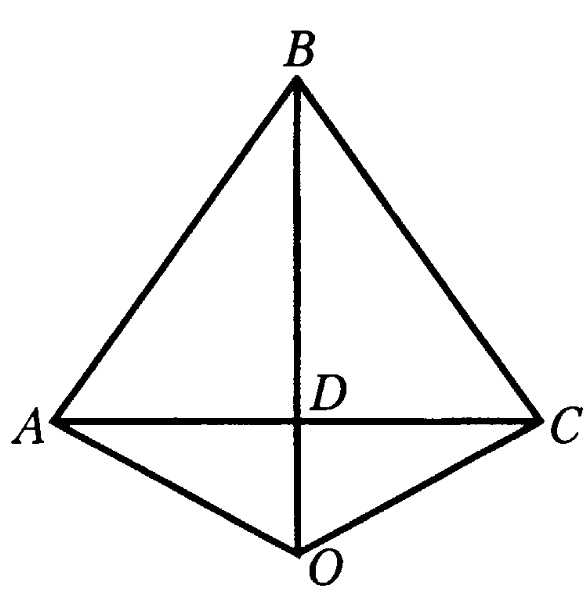
Задача на оценку «5» На отрезке АС как на основании построены по разные стороны от него два равнобедренного треугольника АВС и АDС. Докажите, что ВD┴АС. |
| Билет 2. Сформулируйте и докажите теорему, выражающую первый признак равенства треугольников. Сформулируйте теорему о высоте равнобедренного треугольника. Какой отрезок называется биссектрисой треугольника? Сколько биссектрис имеет треугольник? Задача на оценку «3» Треугольники АВС и KLM равны. Известно, что KL = АВ, LM = ВС. Найдите соответствующие углы треугольника KLM, если угол АВС = 730, угол ВСА = 370. Задача на оценку «4» На рисунке соответственные стороны АD и ВС треугольников АDC и АВС равны, а угол DАС равен углу АСВ. Найдите угол ВАС, если угол DCA =105°. 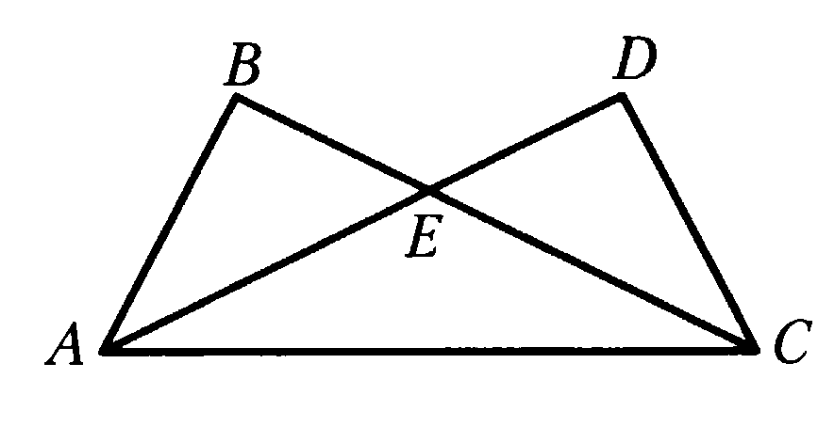
Задача на оценку «5» На рисунке ⦟ВАС=⦟F, ⦟1=⦟2, АD=CF, ⦟Е=90°, ЕF=15 дм. Найдите высоту треугольника АМС, проведенную из вершины А. 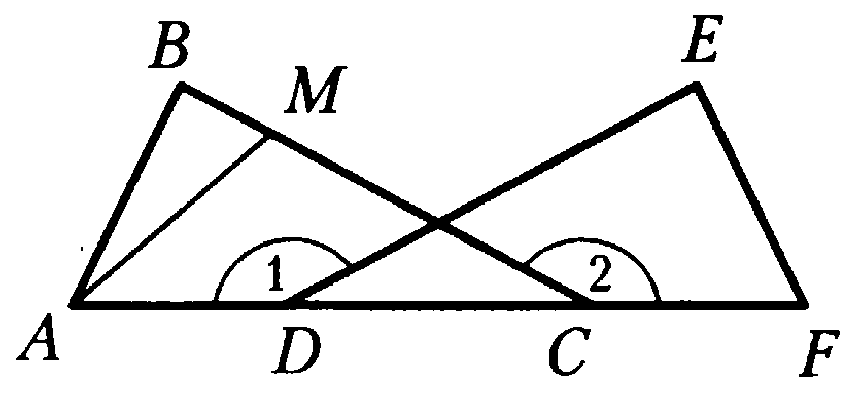
|
| Билет 3. Сформулируйте и докажите теорему, выражающую третий признак равенства треугольников (первый случай). Какой треугольник называется равнобедренным? Как называются его стороны? Какой отрезок называется медианой треугольника. Сколько медиан имеет треугольник? Задача на оценку «3» На рисунке АО=СО, ВО=DO, АВ=5 см. Найдите СD. 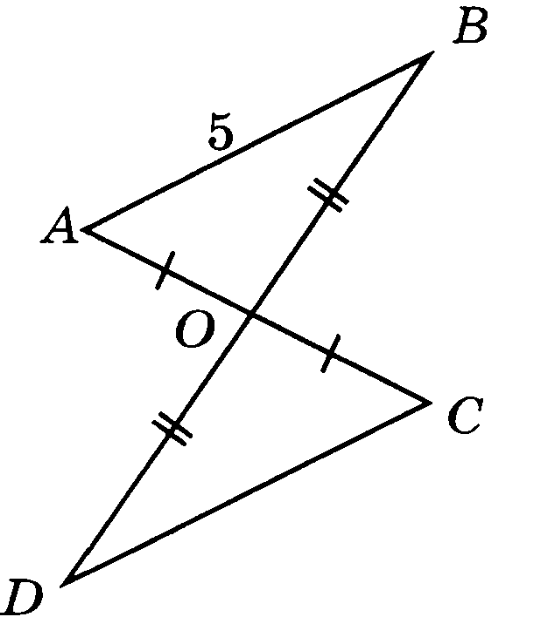 Задача на оценку «4» Две стороны треугольника равны 5 см и 3 см. Медиана, проведённая к третьей стороне, делит данный треугольник на два. Найдите разность периметров этих треугольников. Задача на оценку «5» На Рисунке АЕ=ЕС и ВЕ=ЕD. Докажите, что ⦟АСD=⦟САВ. 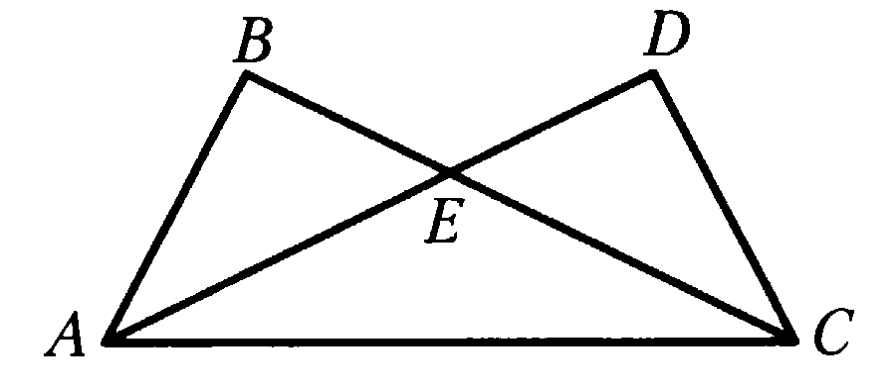
|
| Билет 4. Сформулируйте и докажите теорему, выражающую третий признак равенства треугольников (второй случай). Объясните, какой отрезок называется перпендикуляром, проведённым из данной точки к данной прямой. Какой треугольник называется равносторонним? Начертите треугольник и покажите его стороны, вершины и углы. Задача на оценку «3» Может ли высота треугольника находиться вне его? Задача на оценку «4» На рисунке ВD=BF, AD=CF. Докажите, что 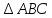 -равнобедренный -равнобедренный 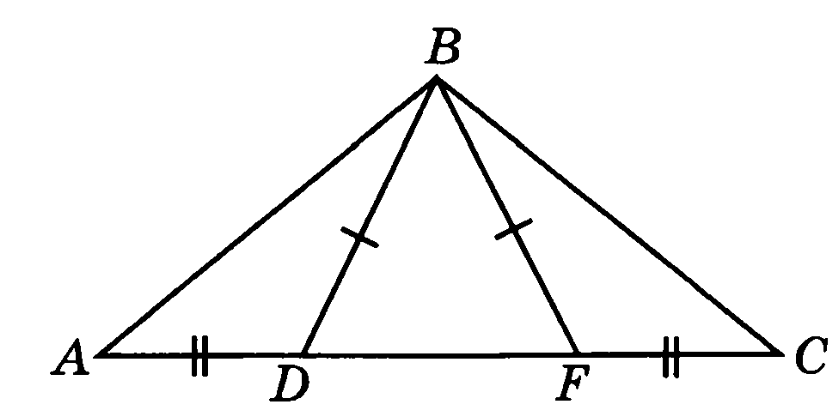
Задача на оценку «5» На рисунке ∆ВСN=∆DAM, DM-медианы треугольника АDO, BN-медиана треугольника СВО. Докажите, что ∆АВN=∆CDM. 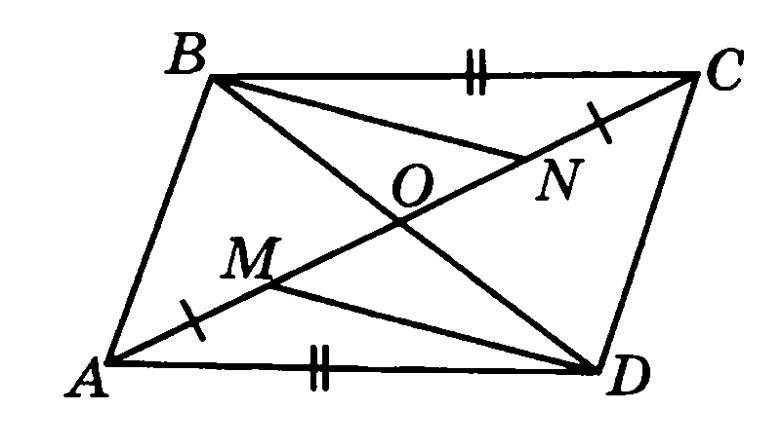
|
| Билет 5. Сформулируйте и докажите теорему, выражающую третий признак равенства треугольников (третий случай). Сформулируйте теорему о биссектрисе равнобедренного треугольника. Объясните, какая фигура называется треугольником. Начертите треугольник и покажите его стороны, вершины и углы. Что такое периметр треугольника? Задача на оценку «3» В равнобедренном треугольнике боковая сторона равна 7 см, а основание – 4 см. Вычислите периметр треугольника. Задача на оценку «4» Отрезки АF и СЕ – биссектрисы углов САВ и АСВ соответственно, угол САВ равен углу АСВ. Докажите равенство треугольников АFС и САЕ 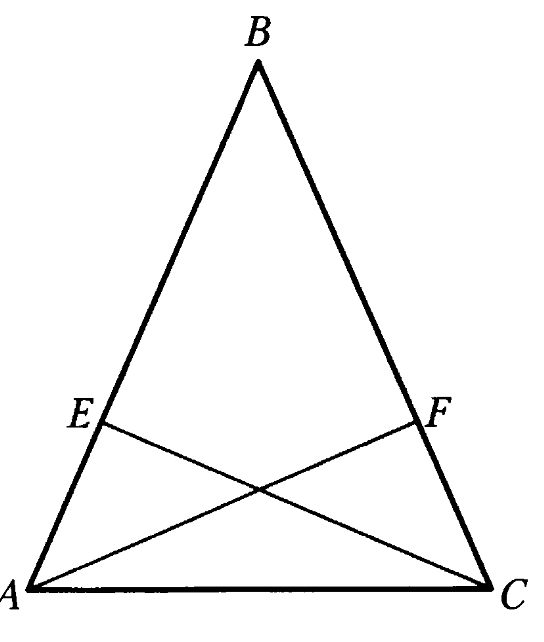
Задача на оценку «5» В треугольнике АВС угол А = 380, угол В = 1100, угол С = 320. На стороне АС отмечены точки D и Е так, что точка D лежит на отрезке АЕ, ВD = DА, ВЕ = ЕС. Найдите угол DВЕ. |
| Билет 6. Сформулируйте и докажите теорему о биссектрисе равнобедренного треугольника. Какие треугольники называют равными? Сформулируйте теорему, выражающую первый признак равенства треугольников. Задача на оценку «3» В равностороннем треугольнике сторона равна 7 см. Вычислите периметр треугольника. Задача на оценку «4» ![]() На сторонах угла А отложены равные отрезки АВ и АС, а на биссектрисе угла А отмечена точка D. Докажите, что треугольник DСВ равнобедренный. Укажите его основание. Задача на оценку «5» Внутри равнобедренного треугольника АВС с основанием АС отмечена точка О так, что АО = ВО = СО. Прямая ВО пересекает сторону АС в точке D. а) Докажите, что отрезок ВD является медианой, биссектрисой и высотой данного треугольника. б) Определите угол ВАО и угол ВСО, если угол АВС = 800.
|
| Билет 7 Докажите, что углы при основании равнобедренного треугольника равны. Сформулируйте теорему, выражающую второй признак равенства треугольников. Объясните, какой отрезок называется перпендикуляром, проведённым из данной точки к данной прямой. Задача на оценку «3»     ∆СDЕ =∆ КFМ – равносторонние. Найдите периметр ∆ КFМ, если сторона СD = 10 см. Задача на оценку «4» Периметр треугольника АВС равен 15 см. Сторона ВС больше стороны АВ на 2 см, а сторона АВ меньше стороны АС на 1 см. Найдите стороны треугольника. Задача на оценку «5» Треугольники АВD и DВС – равнобедренные с равными основаниями АD и СD. Докажите, что: а) АВD = СВD; б) медианы ВМ и ВК этих треугольников равны.
|
|   Билет 8 Билет 8
Сформулируйте и докажите теорему о перпендикуляре, проведённом из данной точки к данной прямой. Сформулируйте теорему, выражающую третий признак равенства треугольников. Какими свойствами обладает равнобедренный треугольник? Задача на оценку «3» 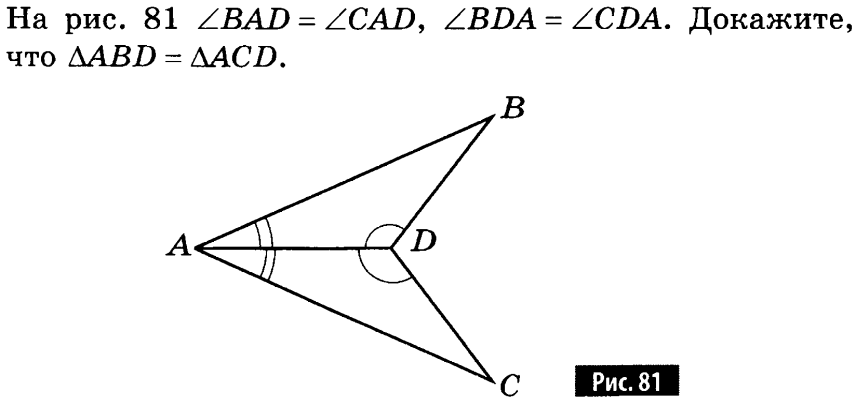
Задача на оценку «4» Периметр треугольника равен 165 см, а его стороны относятся как 3:7:5. Найдите стороны треугольника. Задача на оценку «5» По одну сторону от прямой АВ отмечены точки С и D так, что угол САВ равен углу DВА и DВ = СА. Докажите равенство треугольников АDВ и ВСА.
|
| Билет 9 Сформулируйте и докажите теорему о медиане равнобедренного треугольника. Какой треугольник называется равнобедренным? Как называются его стороны? Объясните, какой отрезок называется перпендикуляром, проведённым из данной точки к данной прямой. Задача на оценку «3» В треугольниках АВС и ВАD ⦟CAB=⦟DBA, ⦟CBA=⦟DAB, AD=2 см. Найдите ВС. Задача на оценку «4» Найдите стороны равнобедренного треугольника, периметр которого равен 127 см, а боковая сторона на 5 см больше основания. Задача на оценку «5» К прямой а проведены перпендикулярные прямые АС и ВD, причём АС = ВD. Точки С и D принадлежат прямой а. Докажите, что АDВ = ВDС.
|












 -равнобедренный
-равнобедренный