Урок № ____ Дата: __.__.___ Класс: 7 Предмет: алгебра
Тема урока: Прямая пропорциональность и ее график
Цели урока
Образовательные: уметь правильно употреблять функциональную терминологию, ввести понятие прямой пропорциональности.
Развивающие: способствовать развитию умений ставить перед собой цели и добиваться их решения; развивать интеллектуальную сферу: внимание, память, речь, мышление; развивать эмоциональную сферу: уверенность в себе; развивать мотивационную сферу: стремление добиться успехов; развивать коммуникативную сферу: навыки работы в парах и группах.
Воспитательные: способствовать развитию у обучающегося заботливого отношения к своему здоровью; воспитывать целостное восприятие мира; формировать познавательный интерес к предмету.
Планируемые результаты урока:
Предметные: уметь правильно употреблять функциональную терминологию, изучить понятие прямой пропорциональности.
Личностные: осознавать значимость знаний, формировать адекватную самооценку, уметь видеть и признавать свои ошибки, развитие готовности к решению творческих задач, умения находить адекватные способы поведения и взаимодействия с партнёрами во время учебной деятельности, способности оценивать проблемные ситуации и оперативно принимать ответственные решения в различных продуктивных видах деятельности.
Метапредметные:
Регулятивные УУД: сформировать умения самостоятельно формулировать учебную проблему, определять цель учебной деятельности, выдвигать версии решения проблемы, работать по алгоритму с правилами по формированию общих приемов учебной деятельности по усвоению химических понятий.
Коммуникативные УУД: сформировать умение организовывать учебное сотрудничество с учителем и сверстниками; умение самостоятельно организовывать свою работу по закреплению материала; умение владеть устной речью.
Познавательные УУД: сформировать умение ориентироваться в своей системе знаний, находить и использовать нужную информацию, строить логическое рассуждение, включающее установление причинно-следственных связей, анализировать и обобщать изученную информацию, сравнивать, делать выводы, применение новых знаний в жизненной ситуации.
Тип урока: Комбинированный урок
Оборудование: тетради, учебник, дид. материалы, чертежные принадлежности
Ход урока
1.Организационный момент.
2. Мотивация учебной деятельности учащихся.
Мы хорошо поработали над предыдущей темой! Теперь мы знаем, что такое функция. И теперь мы переходим к изучению еще одной важной темы: сегодня мы узнаем, как строить график прямой пропорциональности.
3. Целеполагание
Итак, дети, какая цель нашего урока?
4. Актуализация накопленного опыта и опорных знаний учащихся, проверка домашнего задания.
- Что такое функция? Дайте определение независимой переменной или аргументу. А зависимой переменной или функции?
- Дайте определение области определения функции. (Все значения, которые может принимать независимая переменная)
- Задайте формулой какую-нибудь функцию, область определения которой:
а) все действительные числа; б) только положительные числа;
- Графиком функции называется множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции.
- По точкам можно построить график любой функции, заданной таблично или аналитически (с помощью формулы).
– Как по графику найти значение функции, соответствующее данному значению аргумента?
– Как по графику найти значения аргумента, которым соответствует данное значение функции?
– Как, не строя график, выявить принадлежность ему точки с данными координатами?
– Как, не строя график, определить, в каких точках он пересекает ось абсцисс; ось ординат?
5. Восприятие и усвоение учащимися нового учебного материала.
Введение понятия основывается на рассмотрении конкретных практических примеров. Желательно их привести несколько.
Пример. Прямо пропорциональное отношение: цена - сумма
Чем выше цена товара, тем большую сумму нужно за одно и то же его количество заплатить.
Например: Вы хотите купить 1 кг конфет.
При цене 70 рублей за 1 кг заплатите 210 рублей. При цене 200 руб. за 1 кг заплатите 600 рублей. Чем выше цена, тем выше необходимая сумма.
Кроме того, представить уже знакомую учащимся задачу: «Вычислить площадь прямоугольника, основание которого равно 3, а высота равна х». Если искомую площадь обозначить буквой у, то ответ можно записать формулой: у = 3х.
Если основание прямоугольника равно k, то зависимость между высотой х и площадью у выразится формулой у = kх.
Каждое заданное значение числа k определяет некоторую функцию
у = kх. Затем формулируем четкое определение:
Прямой пропорциональностью называется функция, которую можно задать формулой вида у = kх, где х – независимая переменная, k – не равное нулю число или коэффициент прямой пропорциональности.
График прямой пропорциональности – это прямая, проходящая через начало координат.
2. Просим учащихся привести примеры прямой пропорциональности и примеры функций, не являющихся прямой пропорциональностью.
График прямой пропорциональности.
1) График прямой пропорциональности является прямой, проходящей через начало координат.
2) Если коэффициент пропорциональности k 0, то график расположен в первой и третьей координатных четвертях.
3) Если коэффициент пропорциональности k
На основе этого учащиеся выводят алгоритм построения графика ПП:
1-й шаг. Для х1 0 вычислить у1 по формуле у = kх.
2-й шаг. Отметить в координатной плоскости точки с координатами (0; 0) и (х1; у1).
3-й шаг. Провести прямую через построенные точки.
Первичное применение приобретенных знаний
Так, следует рассмотреть пример со с. 69 учебника; Примеры 1,2,3 стр. 70. - устно
Физминутка.
6. Применение учащимися знаний и действий в стандартных условиях с целью усвоения навыков (тренировочные упражнения).
Решить № 297, 301. - письменно
7. Творческий перенос знаний и навыков в новые условия с целью формирования умений (творческие упражнения).
1.Найдите область определения функции.
а) y = 3x + 2; б) y = 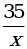 ; в) y =
; в) y = 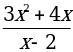 ;г) y =
;г) y = 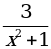 ; д) y =
; д) y = 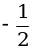 x;
x;
е) y = 2x2 + 6x + 1.
Дополнительно:
2.Является ли функция прямой пропорциональностью:
б) y = 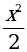 ; в) y =
; в) y = 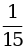 x д) y =
x д) y = 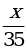 ;
;
г) y = –17x2; е) y = 3x + 11 а) y = 182x;
3.Функция задана формулой у = kх. Найдите коэффициент прямой пропорциональности k, если:
а) х = 2; у = 4; б) x = 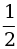 ; y = –4; в) х = 3; у =
; y = –4; в) х = 3; у = 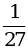 ; г) х = 0; у = 0.
; г) х = 0; у = 0.
4.Затем заполнить таблицу значений функции при –4 ≤ х ≤ 4 с шагом 0,5.
При выполнении этого задания повторяем с учащимися правило нахождения по графику значения функции по данному значению аргумента и наоборот (отмечаем точку на оси абсцисс; проводим прямую, перпендикулярную оси абсцисс, до пересечения с графиком функции; из полученной точки опускаем перпендикуляр на ось ординат и находим соответствующее числовое значение ординаты).
Также на этом примере показываем, что очень важен выбор правильной величины единичного отрезка. Если взять в качестве единицы измерения одну клеточку, то будет очень неудобно строить график, точки будут «слипаться», чертеж будет грязным и нефункциональным.
При больших значениях аргумента или функции (у = –150) удобнее работать с формулой и выполнять действия аналитически (решить уравнение; вычислить по формуле).
Индивидуальные задания
Карточка 1
1.Ответить письменно.
– Сформулируйте определение прямой пропорциональности.
– Приведите примеры прямой пропорциональности.
– Как называется число k в записи формулы прямой пропорциональности у = kх? Какое это число?
– Почему данная функция получила свое название?
2. Выберите прямую пропорциональность.
а) y = 3x + 11 б) y = 182*x;
3. Постройте график функции, заданной формулой у = 2х + 1
4. Постройте в координатной плоскости прямую проходящую через точки
(–4; 3) и (3; –1). Найдите координаты точек, в которых эта прямая пересекает ось х и ось у.
5. Решите уравнение. а) 3х = 12; б) х + 2 = х.
Карточка 2
1.Ответить письменно.
– Сформулируйте определение прямой пропорциональности.
– Приведите примеры прямой пропорциональности.
– Как называется число k в записи формулы прямой пропорциональности у = kх? Какое это число?
– Почему данная функция получила свое название?
2. Выберите прямую пропорциональность (несколько вариантов ответов)
а) y = 3x + 11 б) y = 182*x;
в) y = 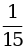 x д) y =
x д) y = 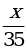 ; г) y =
; г) y = 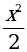 ;
;
3. Построить график функции у = - 0,8х и найти по графику:
а) значение функции, если значение аргумента равно - 2;
б) значение аргумента, если значение функции равно 4.
4. Постройте в координатной плоскости прямую, проходящую через точки А (3; 4) и В (–5; –1). Найдите координаты точек, в которых эта прямая пересекает ось х и ось у.
5. 3. Решите уравнение. а) –2х + 14 = 0; б) х – 15 = 2;
Карточка 3
1.Ответить письменно.
– Сформулируйте определение прямой пропорциональности.
– Приведите примеры прямой пропорциональности.
– Как называется число k в записи формулы прямой пропорциональности у = kх? Какое это число?
– Почему данная функция получила свое название?
2. Найдите значение функции у = 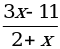 для следующих значений аргумента:
для следующих значений аргумента:
а) 0; б) 4; в) –4; г) –2.
3. Выберите прямую пропорциональность (несколько вариантов ответов)
а) y = 3x + 11 б) y = 182*x;
в) y = 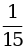 x д) y =
x д) y = 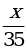 ; г) y =
; г) y = 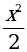 ;
;
4. Решите уравнение.
а) 3х +12 = – 2х + 14 в) х – 16 = 2х + 2
5. Задайте прямую пропорциональность формулой, если известно, что её график проходит через точку В(-3; 7).
6. Подведение итогов урока (рефлексия) и сообщение домашнего задания
П. 15 № 298, 308,309






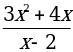 ;г) y =
;г) y = 









