
Свойства биссектрисы угла
(четыре замечательные точки треугольника)

Третья замечательная точка треугольника – точка пересечения высот (или их продолжений) – ортоцентр.
Последняя замечательная точка – точка пересечения медиан.
три медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершины.

В С П О М Н И:
- Что называется :
- Медианой треугольника;
- Биссектрисой треугольника;
- Высотой треугольника;
- Серединным перпендикуляром к отрезку

- Медианой треугольника называется отрезок, соединяющий любую вершину треугольника с серединой противоположной стороны.
- Биссектрисой треугольника называется отрезок биссектрисы любого угла от вершины до пересечения с противоположной стороны
- Высотой треугольника называется перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на ее продолжение.
- Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярно к нему.

Теорема
Каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон.
Oбратно: каждая точка, лежащая внутри угла и равноудалённая от сторон угла, лежит на его биссектрисе.
Дано: ВАС, A Е – биссектриса угла
М ∈ A Е, МК ⊥ АВ , М L ⊥ АС
Доказательство:
1) ∆АКМ = ∆А L М по гипотенузе и острому углу
(АМ – общая, КАМ = L АМ ) КМ = L М ч.т.д.
2) Точка М лежит внутри САВ , МК ⊥ АВ, М L ⊥ АС, КМ = L М ,∆АКМ = ∆А L М по общей гипотенузе АМ и катету ( КМ = L М), поэтому КАМ = L АМ , тогда
AL – биссектриса ВАС ч.т.д.
Е

Теорема
Каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон.
Oбратно: каждая точка, лежащая внутри угла и равноудалённая от сторон угла, лежит на его биссектрисе.
Дано: ВАС, A Е – биссектриса угла
М ∈ A Е, МК ⊥ АВ, М L ⊥ АС
Доказательство:
1) ∆АКМ = ∆А L М по гипотенузе и острому углу
(АМ – общая, КАМ = L АМ ) КМ = L М ч.т.д.
2) Точка М лежит внутри САВ , МК ⊥ АВ, М L ⊥ АС, КМ = L М ,∆АКМ = ∆А L М по общей гипотенузе АМ и катету ( КМ = L М), поэтому КАМ = L АМ, тогда
AL – биссектриса ВАС ч.т.д.
Е

Дано: ВАС, A Е – биссектриса угла
М ∈ A Е, МК ⊥ АВ, М L ⊥ АС
Доказательство:
1) ∆АКМ = ∆А L М по гипотенузе и острому углу
(АМ – общая, КАМ = L АМ ) КМ = L М ч.т.д.
2) Точка М лежит внутри САВ , МК ⊥ АВ, М L ⊥ АС, КМ = L М ,∆АКМ = ∆А L М по общей гипотенузе АМ и катету ( КМ = L М), поэтому КАМ = L АМ, тогда
AL – биссектриса ВАС ч.т.д.
Е

Cледствие 1
Геометрическим местом точек плоскости, лежащих внутри неразвёрнутого угла и равноудалённых от сторон угла, является биссектриса этого угла.
Cледствие 2
Биссектрисы треугольника пересекаются в одной точке.
 OL=OM = O лежит на биссектрисе С (на СС₁) = AA1 ∩ BB1 ∩ CC1 = O ч.т.д. " width="640"
OL=OM = O лежит на биссектрисе С (на СС₁) = AA1 ∩ BB1 ∩ CC1 = O ч.т.д. " width="640"
Cледствие 2
Биссектрисы треугольника пересекаются в одной точке.
Дано : Δ ABC,
AA₁, BB₁, CC₁ – биссектрисы Δ ABC
Доказать : AA₁ ∩ BB₁ ∩ CC₁ = O.
Доказательство :
Пусть AA₁ ∩ BB₁ = O, тогда если OK, OM, OL – перпендикуляры из O к сторонам Δ ABC, то OK=OM, OK=OL – по свойству биссектрисы неразвернутого угла = OL=OM = O лежит на биссектрисе С (на СС₁) =
AA1 ∩ BB1 ∩ CC1 = O ч.т.д.

Задание
Внимательно посмотрите видео с доказательством следствия: биссектрисы треугольника пересекаются в одной точке .
Ответьте на вопросы.
- Что называется биссектрисой треугольника?
- Сколько биссектрис в треугольнике?
- Что называется расстоянием от точки до прямой?
- Назовите свойство биссектрисы неразвернутого угла.
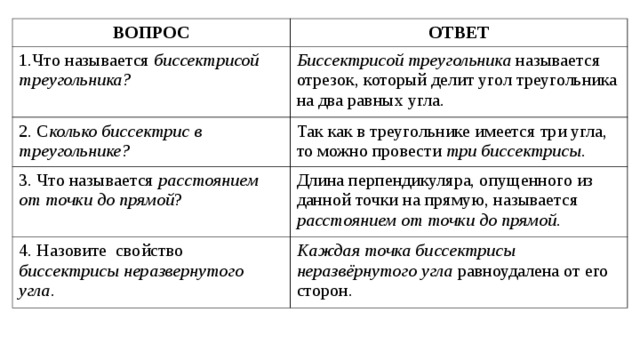
ВОПРОС
ОТВЕТ
1.Что называется биссектрисой треугольника?
Биссектрисой треугольника называется отрезок, который делит угол треугольника на два равных угла.
2. С колько биссектрис в треугольнике?
Так как в треугольнике имеется три угла, то можно провести три биссектрисы .
3. Что называется расстоянием от точки до прямой ?
Длина перпендикуляра, опущенного из данной точки на прямую, называется
расстоянием от точки до прямой.
4. Назовите свойство биссектрисы неразвернутого угла.
Каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон.
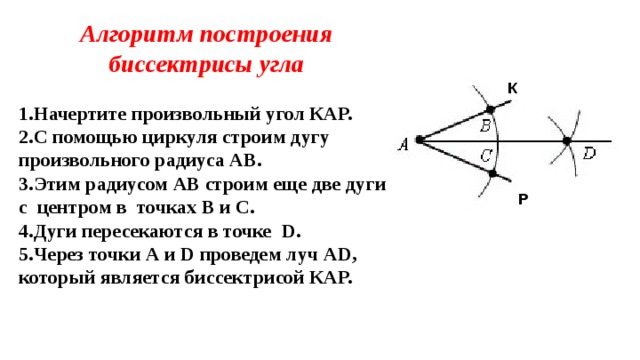
Алгоритм построения биссектрисы угла
- Начертите произвольный угол КАР.
- С помощью циркуля строим дугу произвольного радиуса АВ.
- Этим радиусом АВ строим еще две дуги с центром в точках В и С.
- Дуги пересекаются в точке D .
- Через точки А и D проведем луч А D , который является биссектрисой КАР.
К
Р

Задача 1
Биссектрисы углов А и С треугольника АВС пересекаются в точке М. Найдите угол АВМ, если ∠𝑀𝐴𝐶=30°, ∠𝑀𝐶𝐴=20°
М

Задача 1
Биссектрисы углов А и С треугольника АВС пересекаются в точке М. Найдите угол АВМ, если ∠𝑀𝐴𝐶=30°, ∠𝑀𝐶𝐴=20°
Ответьте на вопросы:
- Почему ВМ-биссектриса АВС ?
- Чему равна сумма углов Δ ?
М

П Р О В Е Р Ь Р Е Ш Е Н И Е
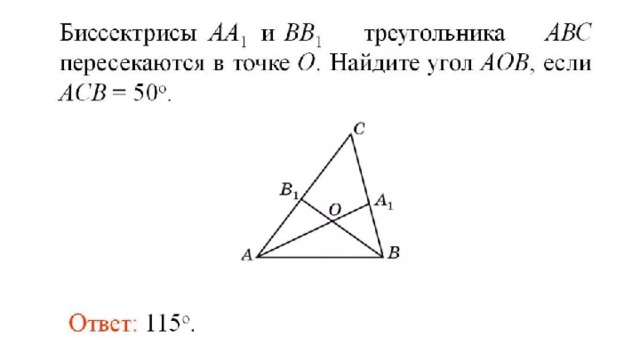

Задание для самостоятельной работы
- Биссектрисы углов А и В треугольника ABC пересекаются в точке М. Найдите ∠AMB, если ∠A= 58°, ∠B = 96°.
- В треугольнике со сторонами 5см, 6 см и 7см постройте точку, равноудаленную от сторон трегольника.
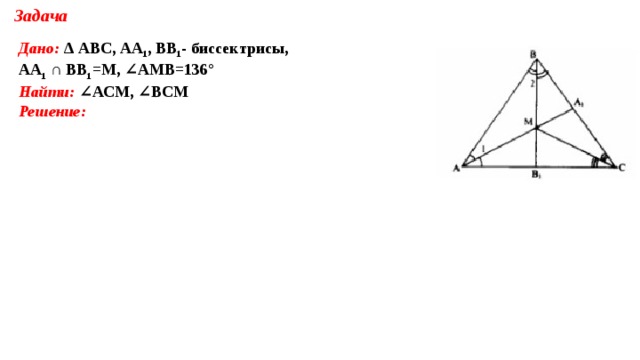
Задача
Дано: Δ АВС, АА 1 , ВВ 1 - биссектрисы,
АА 1 ∩ ВВ 1 =М, ∠АМВ=136°
Найти: ∠АСМ, ∠ВСМ
Решение:
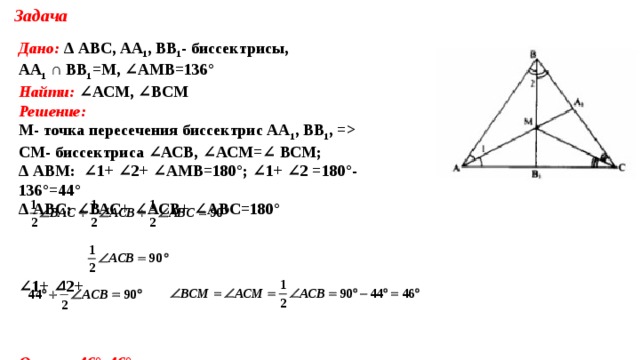 CM- биссектриса ∠АСВ, ∠АСМ=∠ ВСМ; Δ АВМ: ∠1+ ∠2+ ∠АМВ=180°; ∠1+ ∠2 =180°-136°=44° Δ АВС: ∠ВАС+ ∠АСВ+ ∠АВС=180° ∠ 1+ ∠2+ Ответ: 46°, 46° " width="640"
CM- биссектриса ∠АСВ, ∠АСМ=∠ ВСМ; Δ АВМ: ∠1+ ∠2+ ∠АМВ=180°; ∠1+ ∠2 =180°-136°=44° Δ АВС: ∠ВАС+ ∠АСВ+ ∠АВС=180° ∠ 1+ ∠2+ Ответ: 46°, 46° " width="640"
Задача
Дано: Δ АВС, АА 1 , ВВ 1 - биссектрисы,
АА 1 ∩ ВВ 1 =М, ∠АМВ=136°
Найти: ∠АСМ, ∠ВСМ
Решение:
M - точка пересечения биссектрис АА 1 , ВВ 1 , =
CM- биссектриса ∠АСВ, ∠АСМ=∠ ВСМ;
Δ АВМ: ∠1+ ∠2+ ∠АМВ=180°; ∠1+ ∠2 =180°-136°=44°
Δ АВС: ∠ВАС+ ∠АСВ+ ∠АВС=180°
∠ 1+ ∠2+
Ответ: 46°, 46°

Задача в формате ОГЭ(задание 26)
Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 40:1, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 12.
План решения задачи:
1. постройте чертеж и запишите свойство биссектрисы AL в ∆ABL;
2. запишите свойство биссектрисы СL в ∆BLC;
3. введите обозначения AL=x, LC=y и выразите из равенств(пункт 1,2) АВ и СВ через х, у;
4. выразите периметр ∆ABС через переменные х, у;
5. выразите АС=12 см через переменные х, у;
6. вычислите периметр ∆ABС.
 P = 41(x+y) = 41∙12 = 492 Ответ: 492 " width="640"
P = 41(x+y) = 41∙12 = 492 Ответ: 492 " width="640"
Задача в формате ОГЭ(задание 26)
Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 40:1, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 12.
Решение:
Рассмотрим треугольники ∆ ABL и ∆ BLC .
AI - биссектриса ∆ ABL.
По свойству биссектрисы Δ :
Пусть AL=x, тогда AB=40x.
CI – биссектриса ∆ LBC.
По свойству биссектрисы Δ :
Пусть LC=y, тогда CB=40y.
P = AB + CB + AC = 40x + x + y + 40y = 41(x+y)
Заметим, что AC = x+y = 12 .
= P = 41(x+y) = 41∙12 = 492
Ответ: 492

ИТОГИ УРОКА
- Каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон.
- Каждая точка, лежащая внутри угла и равноудалённая от сторон угла, лежит на его биссектрисе.
- Геометрическим местом точек плоскости, лежащих внутри неразвёрнутого угла и равноудалённых от сторон угла, является биссектриса этого угла.
- Биссектрисы треугольника пересекаются в одной точке.

Итак, с каждым треугольником связаны четыре точки:
- точка пересечения медиан,
- точка пересечения биссектрис,
- точка пересечения серединных перпендикуляров к сторонам и точка пересечения высот (или их продолжений).
Эти четыре точки называются замечательными точками треугольника.

З А П О М Н И !
- 1. Точка пересечения биссектрис является центром вписанной окружности.
- 2. Точка пересечения серединных перпендикуляров к сторонам треугольника является центром описанной окружности.
- 3.Точка пересечения медиан, называется центром тяжести треугольника. (Центроид). .
- 4. Точка пересечения высот называется ортоцентр.














 OL=OM = O лежит на биссектрисе С (на СС₁) = AA1 ∩ BB1 ∩ CC1 = O ч.т.д. " width="640"
OL=OM = O лежит на биссектрисе С (на СС₁) = AA1 ∩ BB1 ∩ CC1 = O ч.т.д. " width="640"









 CM- биссектриса ∠АСВ, ∠АСМ=∠ ВСМ; Δ АВМ: ∠1+ ∠2+ ∠АМВ=180°; ∠1+ ∠2 =180°-136°=44° Δ АВС: ∠ВАС+ ∠АСВ+ ∠АВС=180° ∠ 1+ ∠2+ Ответ: 46°, 46° " width="640"
CM- биссектриса ∠АСВ, ∠АСМ=∠ ВСМ; Δ АВМ: ∠1+ ∠2+ ∠АМВ=180°; ∠1+ ∠2 =180°-136°=44° Δ АВС: ∠ВАС+ ∠АСВ+ ∠АВС=180° ∠ 1+ ∠2+ Ответ: 46°, 46° " width="640"

 P = 41(x+y) = 41∙12 = 492 Ответ: 492 " width="640"
P = 41(x+y) = 41∙12 = 492 Ответ: 492 " width="640"













