Методическая разработка урока по геометрии по теме "Теорема Пифагора"

Теорема

Пифагора

О ней писали в своих произведениях римский архитектор и инженер Витрувий, греческий писатель-моралист Плутарх, математик 5 века Прокл и другие. Легенда о том, что в честь своего открытия Пифагор принес в жертву быка или, как рассказывали другие, сто быков, послужила поводом для рассказов писателей и стихов поэтов.

Пребудет Вечной истина, как скоро

Все познает слабый человек!

И ныне теорема Пифагора

Верна, как и в его далекий век.

Обильно было жертвоприношение

Богам от Пифагора. Сто быков

Он отдал на закланье и сожженье

За свет луча, пришедший с облаков.

Поэтому всегда с тех самых пор

  Чуть истина рождается на свет,

Быки ревут, ее почуя, вслед.

Они не в силах свету помешать,

А могут лишь, закрыв глаза, дрожать

  От страха, что вселил в них Пифагор.

Долгое время считали, что до Пифагора эта теорема не была известна. В настоящее время установлено, что эта величайшая теорема встречается в вавилонских текстах, написанных за 1200 лет до Пифагора.

О том, что треугольник со сторонами 3, 4 и 5 есть прямоугольный, знали за 2000 лет до н.э. египтяне, которые, вероятно, пользовались этим отношением для определения прямых углов при построении зданий. На протяжении веков были даны многочисленные доказательства теоремы Пифагора, их существует более 150.

c

b

a

Прямоугольные треугольники с целочисленными сторонами называют египетскими , а тройки целых чисел, для которых выполняется соотношение, связывающее стороны прямоугольного треугольника, – пифагоровыми тройками .

Проверь, являются ли пифагоровыми следующие тройки чисел:    3, 4, 5    5, 12, 13    7, 24, 25?    Придумай два-три примера египетских треугольников, стороны которых образуют пифагоровы тройки.

Доказательство теоремы Пифагора учащиеся средних веков считали очень трудным и называли его Dons asinorum- ослиный мост , или elefuga- бегство “убогих” ,так как некоторые “убогие” ученики, не имевшие серьезной математической подготовки, бежали от геометрии. Слабые ученики, заучившие теоремы наизусть, без понимания, и прозваны по этому “ослами”, были не в состоянии преодолеть теорему Пифагора, служившую для них вроде непреодолимого моста. Из-за чертежей, сопровождающих теорему Пифагора, учащиеся называли ее так же “ветряной мельницей”, составляли стихи вроде “Пифагоровы штаны на все стороны равны”, рисовали карикатуры.

       Н ад озером тихим,        С полфута размером, высился лотоса цвет.        О н рос одиноко. И ветер порывом        О тнес его в сторону. Нет        Б оле цветка над водой,        Н ашел же рыбак его ранней весной        В двух футах от места, где рос.        И так, предложу я вопрос:        К ак озера вода        З десь глубока?

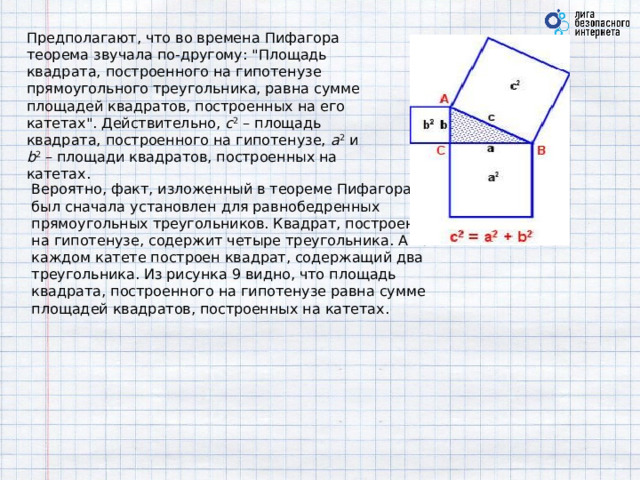
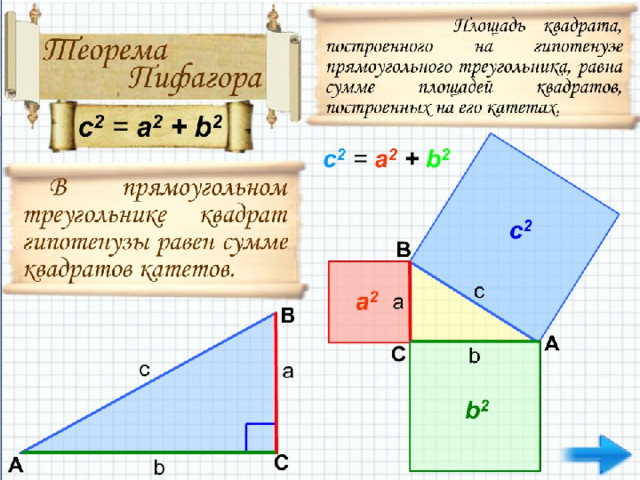
Предполагают, что во времена Пифагора теорема звучала по-другому: "Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах". Действительно, с 2 – площадь квадрата, построенного на гипотенузе, а 2 и b 2 – площади квадратов, построенных на катетах.

Вероятно, факт, изложенный в теореме Пифагора, был сначала установлен для равнобедренных прямоугольных треугольников. Квадрат, построенный на гипотенузе, содержит четыре треугольника. А на каждом катете построен квадрат, содержащий два треугольника. Из рисунка 9 видно, что площадь квадрата, построенного на гипотенузе равна сумме площадей квадратов, построенных на катетах.

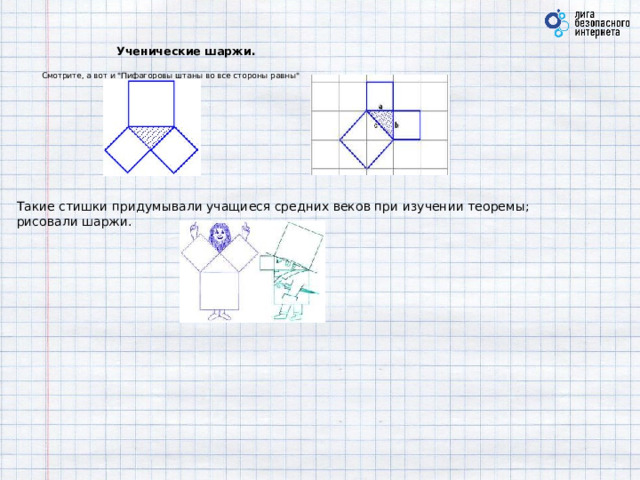
Ученические шаржи. Смотрите, а вот и "Пифагоровы штаны во все стороны равны"

Такие стишки придумывали учащиеся средних веков при изучении теоремы; рисовали шаржи.

Стихи о Пифагоре. Немецкий писатель-романист А. Шамиссо, который в начале Xl X в. Участвовал в кругосветном путешествии на русском корабле «Рюрик», написал следующие стихи: Пребудет вечной истина, как скоро Её познает слабый человек! И ныне теорема Пифагора Верна, как и его далёкий век. Обильно было жертвоприношение Богам от Пифагора. Сто быков Он отдал на закланье и сожженье За света луч, пришедший с облаков. Поэтому всегда с тех самых пор, Чуть истина рождается на свет, Быки ревут, её почуя, вслед. Они не в силах свету помешать, А могут лишь, закрыв глаза, дрожать От страха, что вселил в них Пифагор

В III- IV вв. до н. э. появилась компиляция высказываний Пифагора, известная под названием «Священное слово», из которой позднее возникли так называемые «Золотые стихи».  Заключительный отрывок из «Золотых стихов» в переводе И. Петер: Ты же будь твёрдым: божественный род присутствует в смертных, Им, возвещая, священная всё открывает природа. Если не чуждо это тебе, ты наказы исполнишь, Душу свою исцелишь и от множества бедствий избавишь. Яства, сказал я, оставь те, что я указал в очищеньях. И в избавленье души ко всему подходи с размышленьем. И руководствуйся подлинным знанием — лучшим возничим. Если ты, тело покинув, в свободный эфир вознесёшься, Станешь нетленным, и вечным, и смерти не знающим богом.

Cпособ доказательства теоремы Пифагора.

Т е о р е м а. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Д а н о: Δ АВС , ∠ С = 90°.

Д о к а з а т ь: АВ 2 = АС 2 + ВС 2 .

Д о к а з а т е л ь с т в о

Проведём высоту CD из вершины прямого угла С .

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе, поэтому в Δ ACD    cos A = AD / AC , а в Δ АВС    cos А = AC / AB .

Так как равны левые части этих равенств, то равны и правые, следовательно, AD / AC = AC / AB.

  Отсюда, по свойству пропорции, получаем: АС 2 = AD · АВ .(1)

Аналогично, в Δ ВCD    cos В = BD / BC , а в Δ АВС    cos В = BC / AB .

  Так как равны левые части этих равенств, то равны и правые, следовательно, BD / BC = BC / AB .

  Отсюда, по свойству пропорции, получаем: ВС 2 = ВD · АВ .(2)

Сложим почленно равенства (1) и (2), и вынесем общий множитель за скобки: АС 2 + ВС 2 = AD · AB + BD · AB = AB · ( AD + BD ).

Так как AD + BD = АВ , то АС 2 + ВС 2 = AB · AB = AB 2 .

Получили, что АВ 2 = АС 2 + ВС 2 .

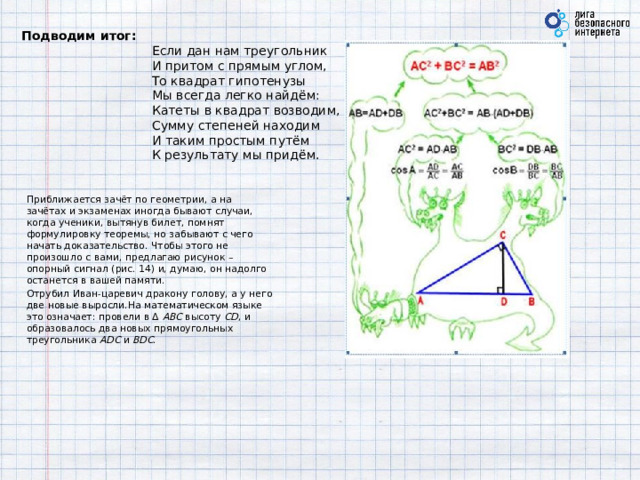
Подводим итог: Если дан нам треугольник И притом с прямым углом, То квадрат гипотенузы Мы всегда легко найдём: Катеты в квадрат возводим, Сумму степеней находим И таким простым путём К результату мы придём.

Приближается зачёт по геометрии, а на зачётах и экзаменах иногда бывают случаи, когда ученики, вытянув билет, помнят формулировку теоремы, но забывают с чего начать доказательство. Чтобы этого не произошло с вами, предлагаю рисунок – опорный сигнал (рис. 14) и, думаю, он надолго останется в вашей памяти.

Отрубил Иван-царевич дракону голову, а у него две новые выросли.На математическом языке это означает: провели в Δ АВС высоту CD , и образовалось два новых прямоугольных треугольника ADC и BDC .

«Не делай никогда того, чего не знаешь, но научись всему, что нужно знать». Пифагор

• В современных учебниках теорема сформулирована так:

«В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов».

Во времена же Пифагора она звучала так:

«Доказать, что квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на катетах».

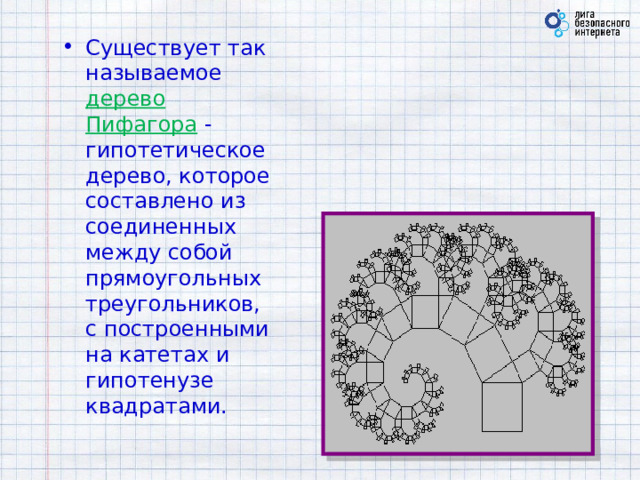
• Существует так называемое дерево Пифагора - гипотетическое дерево, которое составлено из соединенных между собой прямоугольных треугольников, с построенными на катетах и гипотенузе квадратами.

• Существует три формулировки теоремы Пифагора: 1. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. 2. Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на катетах. 3. Квадрат, построенный на гипотенузе прямоугольного треугольника, равносоставлен с квадратами, построенными на катетах.

История открытия теоремы

• Интересна история теоремы Пифагора. Хотя эта теорема и связана с именем Пифагора, она была известна задолго до него.
• В вавилонских текстах эта теорема встречается за 1200 лет до Пифагора, а в Египте это соотношение использовалось для построения прямого угла еще пять тысяч лет назад.
• Возможно, что тогда еще не знали ее доказательства, а само соотношение между гипотенузой и катетами было установлено опытным путем на основе измерений.

Пифагор, по-видимому, нашел доказательство этого соотношения.

• О теореме Пифагора в своих работах писали многие учёные: греческий писатель-моралист Плутарх , математик 5 века Прокл и другие. Возможно, кто-то из вас читал сонет немецкого писателя - романиста Шамиссо:

Пребудет вечной истина, как скоро    Ее познает слабый человек!    И ныне теорема Пифагора    Верна, как и в его далекий век.    Обильно было жертвоприношенье    Богам от Пифагора. Сто быков    Он отдал на закланье и сожженье    За света луч, пришедший с облаков.    Поэтому всегда с тех самых пор,    Чуть истина рождается на свет,    Быки ревут, ее почуя, вслед.    Они не в силах свету помешать ,    А могут лишь закрыв глаза дрожать    От страха, что вселил в них Пифагор.

Способы доказательства теоремы

• Доказательство теоремы считалось в кругах учащихся средних веков очень трудным и называлось "ослиным мостом" или "бегством убогих", а сама теорема - "ветряной мельницей" или "теоремой невест". Учащиеся даже рисовали карикатуры и составляли стишки вроде этого:                Пифагоровы штаны               Во все стороны равны.

ШАРЖИ

Доказательства, основанные на использовании понятия равновеликости фигур

• Древние индусы, которым принадлежит это рассуждение, обычно не записывали его, а сопровождали чертеж лишь одним словом: «Смотри!». Вполне возможно, что такое же доказательство предложил и Пифагор.

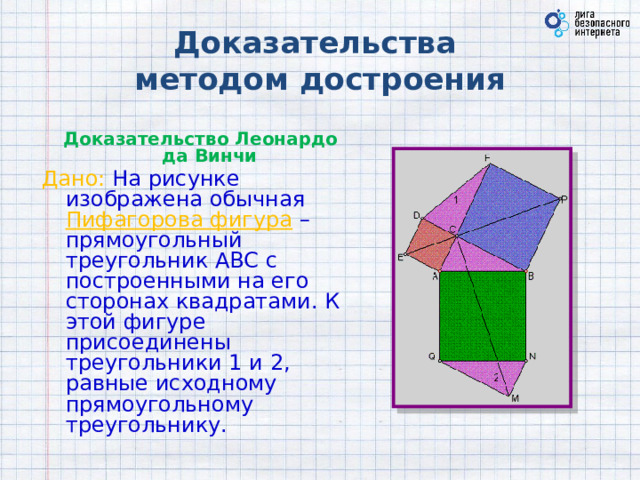
Доказательства методом достроения

Доказательство Леонардо да Винчи

Дано: На рисунке изображена обычная Пифагорова фигура – прямоугольный треугольник ABC с построенными на его сторонах квадратами. К этой фигуре присоединены треугольники 1 и 2, равные исходному прямоугольному треугольнику.

• Доказательство:
• Доказательство:
• Доказательство:
• Доказательство:

• Справедливость теоремы Пифагора вытекает из равновеликости шестиугольников AEDFPB и ACBNMQ. Здесь прямая EP делит шестиугольник AEDFPB на два равновеликих четырехугольника, прямая CM делит шестиугольник ACBNMQ на два равновеликих четырехугольника; поворот плоскости на 90° вокруг центра A отображает четырехугольник AEPB на четырехугольник ACMQ. Поворот четырехугольника CBNM вокруг точки В на 90° по часовой стрелке отображает его на четырехугольник EPBA, который в свою очередь равен четырехугольнику EDFP.

• Теорема доказана.
• Теорема доказана.
• Теорема доказана.
• Теорема доказана.
• Теорема доказана.

Доказательства методом разложения

Доказательство Перигаля

Доказательство Перигаля очень легкое. Два квадрата, построенные на катетах, расположены рядом. Надо разделить эту фигуру всего на 3(!) части, чтобы сложить из них квадрат на гипотенузе. На иллюстрации наглядно дано это разрезание.

Существуют также задачи на теорему Пифагора в стихах.

• Задача Бхаскари

«На берегу реки рос тополь одинокий. Вдруг ветра порыв его ствол надломал. Бедный тополь упал. И угол прямой С теченьем реки его ствол составлял. Запомни теперь, что в этом месте река В четыре лишь фута была широка Верхушка склонилась у края реки. Осталось три фута всего от ствола, Прошу тебя, скоро теперь мне скажи: У тополя как велика высота?»

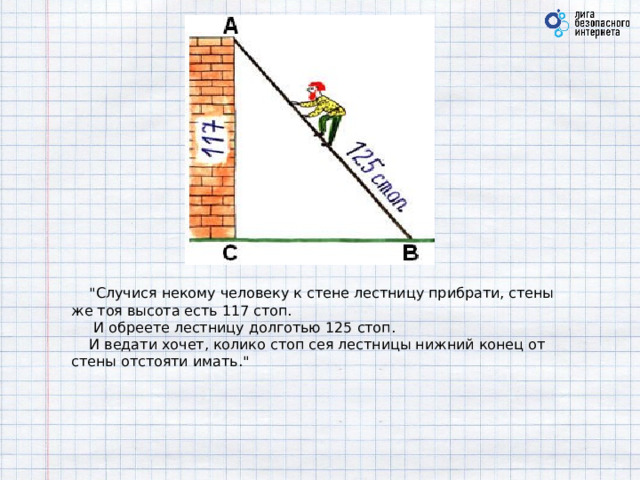
    "Случися некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп.

И обреете лестницу долготью 125 стоп.

    И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать."

    " Имеется водоем со стороной в 1 чжан = 10 чи.

В центре его растет камыш, который выступает над водой на 1 чи.

Если потянуть камыш к берегу, то он как раз коснётся его.

    Спрашивается: какова глубина воды и какова длина камыша?"

ОБЛАСТИ ПРИМЕНЕНИЯ

• Строительство
• Астрономия
• Мобильная связь

Мобильная связь

• Какую наибольшую высоту должна иметь антенна мобильного оператора, чтобы передачу можно было принимать в радиусе R=200 км? (радиус Земли равен 6380 км.)
• Решение:
•        Пусть AB= x , BC=R=200 км , OC= r =6380 км.
• OB=OA+AB OB=r + x.
• Используя теорему Пифагора, получим Ответ: 2,3 км.

Строительство

• Окна
• Крыши
• Молниеотводы

Молниеотвод

• Известно, что молниеотвод защищает от молнии все предметы, расстояние которых от его основания не превышает его удвоенной высоты. Необходимо определить оптимальное положение молниеотвода на двускатной крыше, обеспечивающее наименьшую его доступную высоту.
• Решение:
•        По теореме Пифагора h2≥ a2+b2 , значит h≥(a2+b2)1/2 .

Окна

• В зданиях готического и романского стиля верхние части окон расчленяются каменными ребрами, которые не только играют роль орнамента, но и способствуют прочности окон. На рисунке представлен простой пример такого окна в готическом стиле. Способ построения его очень прост: Из рисунка легко найти центры шести дуг окружностей, радиусы которых равны
• ширине окна (b) для наружных дуг
• половине ширины, (b/2) для внутренних дуг
• Остается еще полная окружность, касающаяся четырех дуг. Т. к. она заключена между двумя концентрическими окружностями, то ее диаметр равен расстоянию между
• этими окружностями, т. е. b/2 и, следовательно,
• радиус равен b/4. А тогда становится ясным и
• положение ее центра.

• В романской архитектуре часто встречается мотив, представленный на рисунке. Если b по-прежнему обозначает ширину окна, то радиусы полуокружностей будут равны R = b / 2 и r = b / 4. Радиус p внутренней окружности можно вычислить из прямоугольного треугольника, изображенного на рис. пунктиром. Гипотенуза этого треугольника, проходящая через точку касания окружностей, равна b/4+p, один катет равен b/4, а другой b/2-p. По теореме Пифагора имеем:
• (b/4+p)=( b/4)+( b/4-p)
• или
• b/16+ bp/2+p=b/16+b/4-bp+p,
• откуда
• bp/2=b/4-bp.
• Разделив на b и приводя подобные члены, получим:
• (3/2)p=b/4, p=b/6.

Астрономия

• На этом рисунке показаны точки A и B и путь светового луча от A к B и обратно. Путь луча показан изогнутой стрелкой для наглядности, на самом деле, световой луч - прямой.
• Какой путь проходит луч? Поскольку свет идет туда и обратно одинаковый путь, спросим сразу: чему равно расстояние между точками?

• На этом рисунке показан путь светового луча только с другой точки зрения, например из космического корабля. Предположим, что корабль движется влево. Тогда две точки, между которыми движется световой луч, станут двигаться вправо с той же скоростью. Причем, в то время, пока луч пробегает свой путь, исходная точка A смещается и луч возвращается уже в новую точку C.

• В конце девятнадцатого века высказывались разнообразные предположения о существовании обитателей Марса подобных человеку. В шутку, хотя и не совсем безосновательно , было решено п ередать обитателям Марса сигнал в виде теоремы Пифагора . Неизвестно, как это сделать; но для всех очевидно, что математический факт, выражаемый теоремой Пифагора имеет место всюду и поэтому похожие на нас обитатели другого мира должны понять такой сигнал.

Строительство крыши

         При строительстве домов и коттеджей часто встает вопрос о длине стропил для крыши, если уже изготовлены балки. Например: в доме задумано построить двускатную крышу (форма в сечении). Какой длины должны быть стропила, если изготовлены балки AC=8 м., и AB=BF.

      Решение:

      Треугольник ADC - равнобедренный AB=BC=4 м., BF=4 м. Если предположить, что FD=1,5 м., тогда:

      А) Из треугольника DBC: DB=2,5 м.,

      Б) Из треугольника ABF:

Теорема

Пифагора

Пифагор Самосский

(ок. 580 – ок. 500 г. до н.э.)

Открытия пифагорейцев

Пифагорейцами было сделано много важных открытий в арифметике и геометрии, в том числе:

• теорема о сумме внутренних углов треугольника;
• построение правильных многоугольников и деление плоскости на некоторые из них;
• геометрические способы решения квадратных уравнений;
• деление чисел на чётные и нечётные, простые и составные; введение фигурных, совершенных и дружественных чисел;
• доказательство того, что корень из 2 не является рациональным числом;
• создание математической теории музыки и учения об арифметических, геометрических и гармонических пропорциях и многое другое.

Поворотная симметрия 5 -го порядка

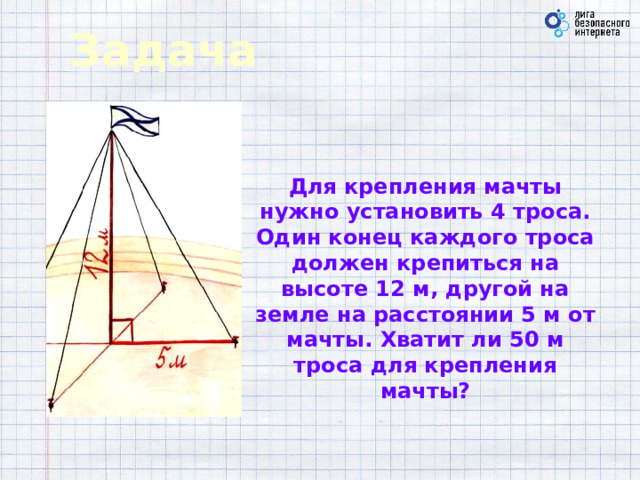
Задача

Для крепления мачты нужно установить 4 троса. Один конец каждого троса должен крепиться на высоте 12 м, другой на земле на расстоянии 5 м от мачты. Хватит ли 50 м троса для крепления мачты?

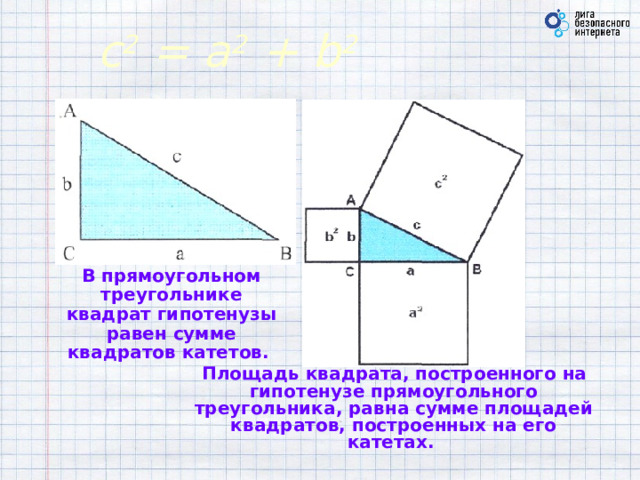
c 2 = a 2 + b 2

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах.

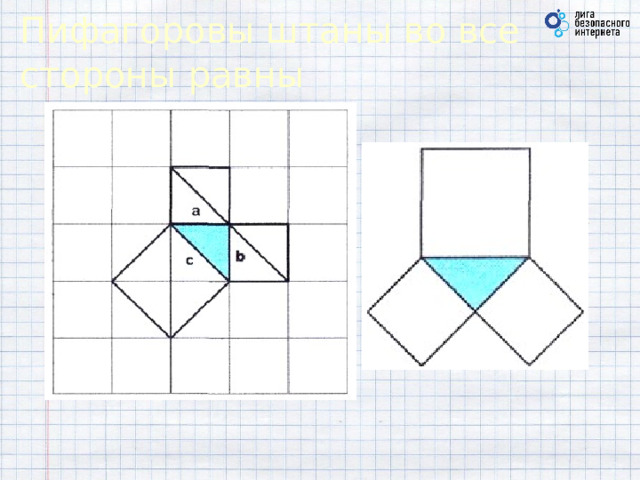
Пифагоровы штаны во все стороны равны

Шаржи

Теорема. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Теорема в стихах

Итак,

Если дан нам треугольник

И притом с прямым углом,

То квадрат гипотенузы

Мы всегда легко найдём:

Катеты в квадрат возводим,

Сумму степеней находим –

И таким простым путём

К результату мы придём.

Ч.т.д.

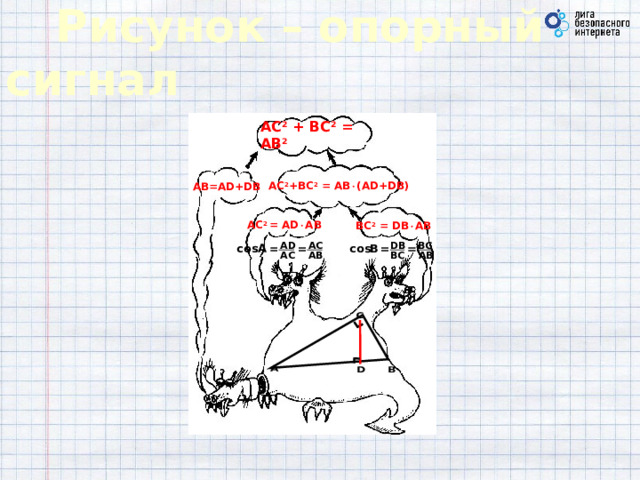
Рисунок – опорный сигнал

АС 2 + ВС 2 = АВ 2

АВ=AD+DB

AC 2 +BC 2 = AB  (AD+DB)

AC 2 = AD  AB

BC 2 = DB  AB

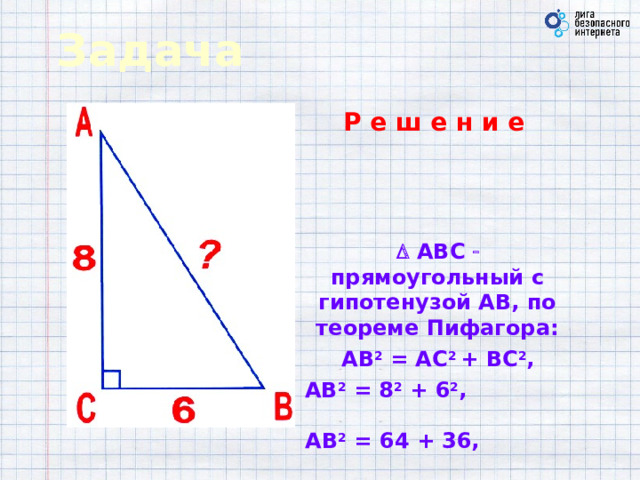
Задача

Р е ш е н и е

 АВС  прямоугольный с гипотенузой АВ, по теореме Пифагора:

АВ 2 = АС 2 + ВС 2 ,

АВ 2 = 8 2 + 6 2 , АВ 2 = 64 + 36, АВ 2 = 100,

АВ = 10 .

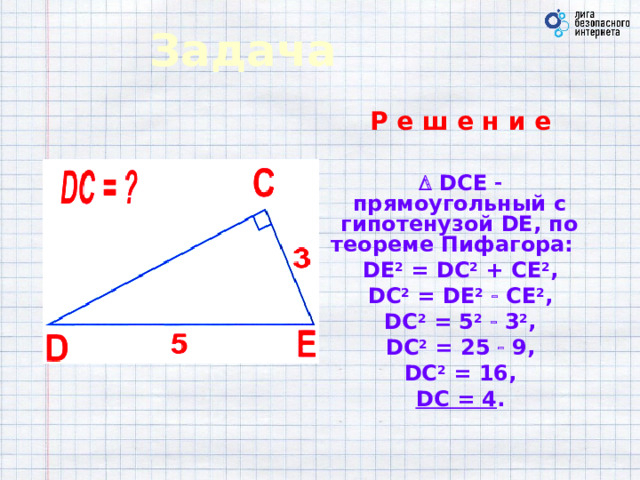
Задача

Р е ш е н и е

 DCE  прямоугольный с гипотенузой DE, по теореме Пифагора:

DE 2 = DС 2 + CE 2 ,

DC 2 = DE 2  CE 2 ,

DC 2 = 5 2  3 2 ,

DC 2 = 25  9,

DC 2 = 16,

DC = 4 .

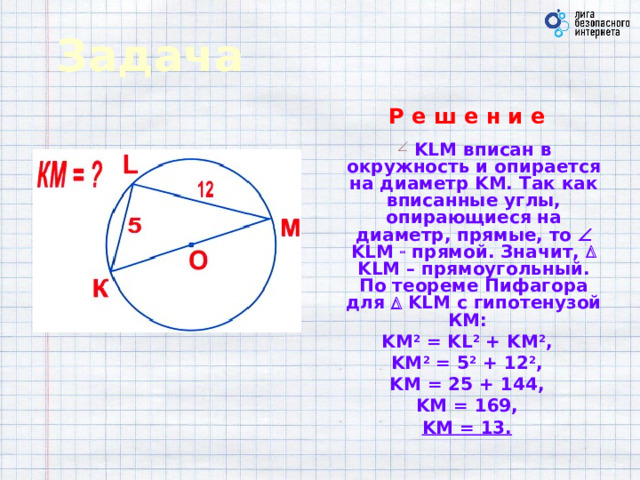
Задача

Р е ш е н и е

• KLM вписан в окружность и опирается на диаметр KM. Так как вписанные углы, опирающиеся на диаметр, прямые, то  KLM  прямой. Значит,  KLM – прямоугольный. По теореме Пифагора для  KLM с гипотенузой КМ:

KM 2 = KL 2 + KM 2 ,

KM 2 = 5 2 + 12 2 ,

KM = 25 + 144,

KM = 169,

KM = 13.

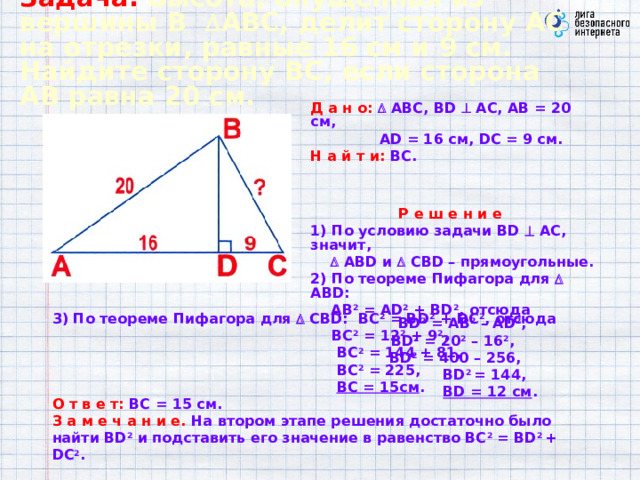
Задача. Высота, опущенная из вершины В  АВС, делит сторону АС на отрезки, равные 16 см и 9 см. Найдите сторону ВС, если сторона АВ равна 20 см.

Д а н о:  АВС, BD  АС, АВ = 20 см,

AD = 16 см, DC = 9 см.

Н а й т и: ВС.

Р е ш е н и е

1) По условию задачи BD  АС, значит,

 ABD и  CBD – прямоугольные.

2) По теореме Пифагора для  ABD:

АВ 2 = AD 2 + BD 2 , отсюда BD 2 = AB 2 – AD 2 ,

BD 2 = 20 2 – 16 2 ,

BD 2 = 400 – 256,

BD 2 = 144,

BD = 12 см .

3) По теореме Пифагора для  СBD: ВС 2 = ВD 2 + DС 2 , отсюда BC 2 = 12 2 + 9 2 , BC 2 = 144 + 81, BC 2 = 225, BC = 15см . О т в е т: ВС = 15 см. З а м е ч а н и е. На втором этапе решения достаточно было найти BD 2 и подставить его значение в равенство ВС 2 = ВD 2 + DС 2 .

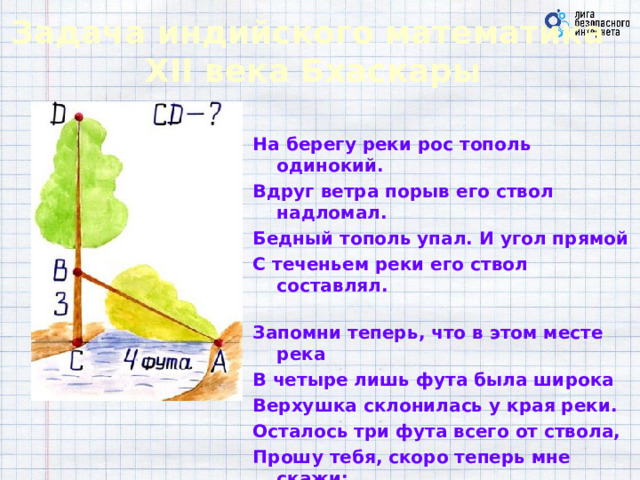
Задача индийского математика XII века Бхаскары

На берегу реки рос тополь одинокий.

Вдруг ветра порыв его ствол надломал.

Бедный тополь упал. И угол прямой

С теченьем реки его ствол составлял.

Запомни теперь, что в этом месте река

В четыре лишь фута была широка

Верхушка склонилась у края реки.

Осталось три фута всего от ствола,

Прошу тебя, скоро теперь мне скажи:

У тополя как велика высота?»

Задача из китайской «Математики в девяти книгах»

Имеется водоем со стороной в 1 чжан = 10 чи. В центре его растет камыш, который выступает над водой на 1 чи. Если потянуть камыш к берегу, то он как раз коснётся его. Спрашивается: какова глубина воды и какова длина камыша?

Задача из учебника «Арифметика» Леонтия Магницкого

Случися некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать.

Пентаграмма

Мефистофель: Нет, трудновато выйти мне теперь,

Тут кое-что мешает мне немного:

Волшебный знак у вашего порога.

Фауст: Не пентаграмма ль этому виной?

Но как же, бес, пробрался ты за мной?

Каким путем впросак попался?

Мефистофель: Изволили ее вы плохо начертить,

И промежуток в уголку остался,

Там, у дверей, - и я свободно мог вскочить.

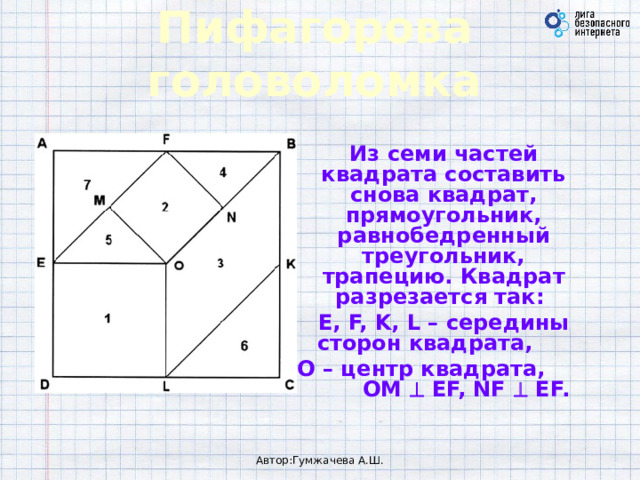
Пифагорова головоломка

Из семи частей квадрата составить снова квадрат, прямоугольник, равнобедренный треугольник, трапецию. Квадрат разрезается так:

E, F, K, L – середины сторон квадрата,

О – центр квадрата, ОМ  EF, NF  EF.

Автор:Гумжачева А.Ш.

Мыслитель,

математик,

философ.

Пифагор

Фрагмент фрески Рафаэля

«Афинская школа».

1511 г.

«Геометрия владеет

двумя сокровищами:

одно из них –

это теорема Пифагора»

Иоганн Кеплер

Теорема Пифагора!

Без преувеличения можно сказать, что это самая известная теорема геометрии, ибо о ней знает подавляющее большинство населения планеты, хотя доказать ее способна лишь очень незначительная его часть.

Теорема Пифагора – одна из самых главных теорем геометрии. Из нее или с ее помощью можно вывести большинство теорем. Сама же теорема Пифагора замечательна тем, что она проста, но не очевидна. Это сочетание двух противоречивых начал и придает ей особую притягательную силу, делает ее красивой. Но, кроме того, теорема Пифагора имеет огромное практическое значение: она применяется в геометрии буквально на каждом шагу.

В чем же причина такой популярности

«пифагоровых штанов»?

Знатоки утверждают, что причин здесь три:

а) красота,

б) простота,

в) значимость.

Знаменитый греческий философ и математик Пифагор Самосский, именем которого названа теорема, жил около 2,5 тысяч лет тому назад. Дошедшие до нас биографические сведения о Пифагоре отрывочны и далеко недостоверны. С его именем связано много легенд.

Пифагор – древнегреческий ученый ( VI в. до н.э.)

Как утверждают все античные авторы, Пифагор первый дал полноценное доказательство теоремы, носящей его имя. К сожалению, мы не знаем, в чем оно состояло, потому что древние математики и писатели об этом умалчивают, а от самого Пифагора и ранних пифагорейцев до нас не дошло ни одного письменного документа.

          Доказательство теоремы считалось в кругах учащихся средних веков очень трудным и называлось:

“ Dons asinorum” -

« ослиный мост»

или

“ elefuga” -

«бегство убогих»

а сама теорема –

«ветряной мельницей»,

«теоремой – бабочкой»

или

«теоремой невесты»

Сейчас известно около 150 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.)

"Dons asinorum"

Теорему называли «мостом ослов», так как слабые ученики, заучивающие теоремы наизусть, без понимания, и прозванные поэтому «ослами», были не в состоянии преодолеть теорему Пифагора, служившую для них вроде непреодолимого моста.

Или «бегство убогих», так как некоторые «убогие» ученики, не имевшие серьезной математической подготовки, бежали от геометрии.

"elefuga"

Не подлежит, однако, сомнению, что эту теорему знали за много лет до Пифагора. Так, за 1500 лет до Пифагора древние египтяне знали о том, что треугольник со сторонами 3, 4 и 5 является прямоугольным, и пользовались этим свойством (т. е. теоремой, обратной теореме Пифагора) для построения прямых углов при планировке земельных участков и сооружений зданий.

Да и поныне сельские строители и плотники, закладывая фундамент избы, изготовляя ее детали, вычерчивают этот треугольник, чтобы получить прямой угол.

Это же самое проделывалось тысячи лет назад при строительстве великолепных храмов в Египте, Вавилоне, Китае, вероятно, и в Мексике.

Как свидетельствуют летописи, в Древнем Китае уже около 2200 года до н.э. для треугольника со сторонами 3, 4, 5 было найдено правило «гоу-гу», с помощью которого можно было по известным гипотенузе и одному из катетов находить другой неизвестный катет, а также гипотенузу, если известны оба катета.

Таким образом, теорема Пифагора в виде простейших угломерных приспособлений, частных и общих математических задач и чертежей обнаружена в памятниках культуры древних египтян, вавилонян, китайцев и индийцев задолго до Пифагора. Но среди этих памятников нет ни одного, за исключением китайского математического трактата, в котором имелись бы хотя бы указания на доказательство теоремы.

К теореме Пифагора его ученики составляли стишки, вроде:

«Пифагоровы штаны

во все стороны равны»,

А также рисовали такие карикатуры:

Шарж из учебника XVI века.

С глубокой древности математики находят все новые и новые доказательства теоремы Пифагора, все новые и новые замыслы ее доказательств. Таких доказательств – более или менее строгих, более или менее наглядных – известно более полутора сотен (по другим источникам, более пятисот), но стремление к преумножению их числа сохранилось. Поэтому теорема Пифагора занесена в «Книгу рекордов Гиннеса». Самостоятельное «открытие» доказательства теоремы Пифагора будет полезно и современным школьникам.

В самом древнем индийском геометрическом сборнике «Сульвасутра» («Правила веревки», 600 год до н.э.), представляющем собой своеобразную инструкцию по сооружению алтарей в храмах, даются правила построения прямых углов при помощи веревки с узлами, расстояния между которыми равны 15, 36 и 39 падас (мера длины). Алтари по священному предписанию должны иметь строгую геометрическую форму, ориентированную относительно четырех сторон горизонта.

5

4

3

Различные способы

доказательства теоремы

• Доказательства, основанные на использовании понятия равновеликости фигур
• Аддитивные доказательства (основаны на разложении квадратов, построенных на катетах, на фигуры, из которых можно сложить квадрат, построенный на гипотенузе
• Доказательства методом достроения
• Алгебраический метод доказательства
• И т.д.

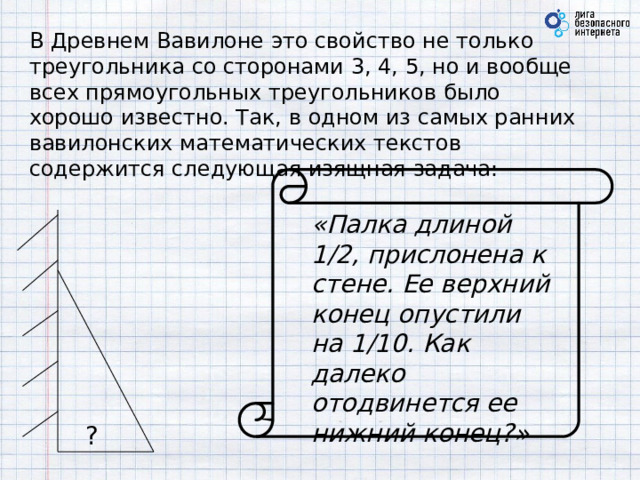
В Древнем Вавилоне это свойство не только треугольника со сторонами 3, 4, 5, но и вообще всех прямоугольных треугольников было хорошо известно. Так, в одном из самых ранних вавилонских математических текстов содержится следующая изящная задача:

«Палка длиной 1/2, прислонена к стене. Ее верхний конец опустили на 1/10. Как далеко отодвинется ее нижний конец?»

?

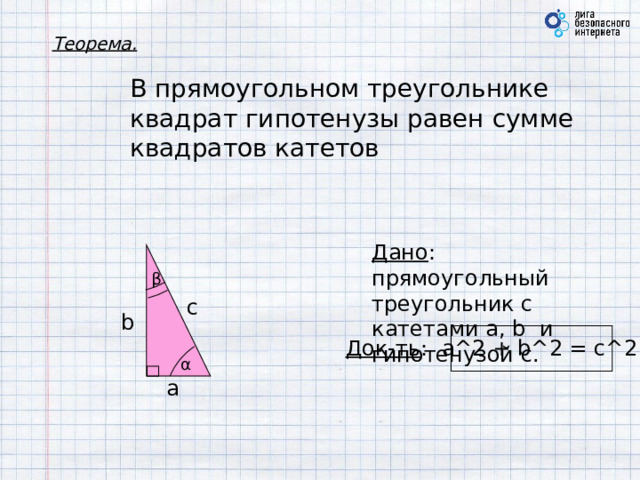
Теорема.

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов

Дано : прямоугольный

треугольник с катетами a, b и гипотенузой c.

β

c

b

Док-ть : a^2 + b^2 = c^2

α

a

b

α

β

α

β

α

β

a

Доказательство:

a

Достроим данный треугольник до квадрата со стороной (a + b) так, как показано на рисунке.

c

b

с

β

c

b

c

a

α

b

a

Sкв. = (a + b)^2 или Sкв. = 4Sтр. + S`кв.

Sтр. = 1/2ab; S`кв. = c^2, тогда

Sкв. = 4 *1/2ab + c^2

Т.о., (a + b)^2 = 4 *1/2ab + c^2

a^2 + 2ab + b^2 = 2ab + c^2

a^2 + b^2 = c^2

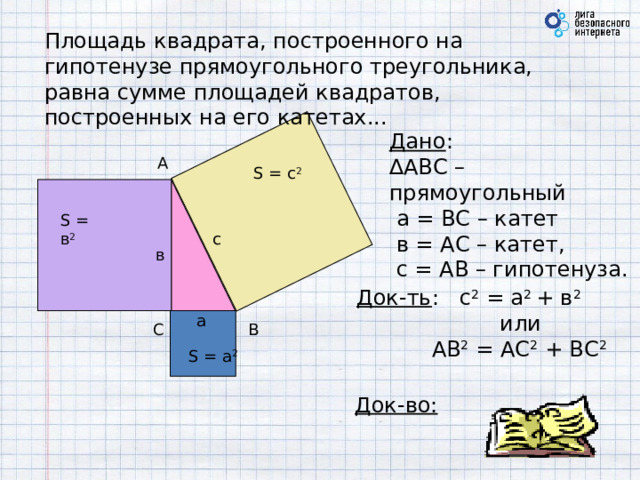
Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах...

Дано :

∆ АВС – прямоугольный

а = ВС – катет

в = АС – катет,

с = АВ – гипотенуза.

A

S = c 2

S = в 2

с

в

Док-ть : с 2 = а 2 + в 2

или

АВ 2 = АС 2 + ВС 2

a

B

C

S = a 2

Док-во:

В некоторых списках «Начал» Евклида теорема Пифагора называлась теоремой Нимфы, «теорема – бабочка», по-видимому из-за сходства чертежа с бабочкой, поскольку словом «нимфа» греки называли бабочек. Нимфами греки называли еще и невест, а также некоторых богинь.

При переводе с греческого арабский переводчик, вероятно, не обратил внимания на чертеж и перевел слово «нимфа» не как «бабочка», а как «невеста». Так и появилось ласковое название знаменитой теоремы – «Теорема Невесты».

«Нимфа» - бабочка, невеста

Теорема Пифагора

pptcloud.ru

Содержание

Биография Пифагора

Пифагорейская школа

Открытия Пифагора

Пифагор и музыка

Теорема Пифагора

Проверь себя

Остров Самос

Пифагор и музыка

Примечательно, что отправным

пунктом в пифагорейском учении о

числе была музыка. По преданию, сам

Пифагор установил, что приятные

слуху созвучия получаются лишь в том

случае, когда длина струн, издающих

эти звуки, относятся как целые числа

первой четверки

1 : 2 2 : 3 3 : 4

Появилась музыкальная октава и гамма.

Пифагор со своими учениками. Иллюстрация из книги Франкино Гафурио «Теория музыки». Милан.1492 г. Гравюра изображает акустические опыты Пифагора на сосудах и трубах, находящихся в отношениях 4 : 6 : 8 : 9 : 12 : 16

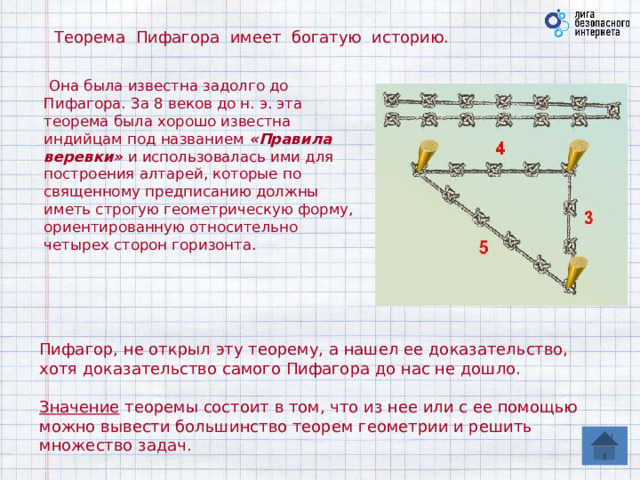
Теорема Пифагора имеет богатую историю.

Она была известна задолго до Пифагора. За 8 веков до н. э. эта теорема была хорошо известна индийцам под названием «Правила веревки» и использовалась ими для построения алтарей, которые по священному предписанию должны иметь строгую геометрическую форму, ориентированную относительно четырех сторон горизонта.

Пифагор, не открыл эту теорему, а нашел ее доказательство, хотя доказательство самого Пифагора до нас не дошло.

Значение теоремы состоит в том, что из нее или с ее помощью можно вывести большинство теорем геометрии и решить множество задач.

В зданиях готического и романского стиля верхние части окон расчленяются каменными ребрами, которые не только играют роль орнамента, но и способствуют прочности окон. На рисунке представлен простой пример такого окна в готическом стиле. Способ построения его очень прост: Из рисунка легко найти центры шести дуг окружностей, радиусы которых равны

1.ширине окна (b) для наружных дуг

2. половине ширины, (b/2) для внутренних дуг

Остается еще полная окружность, касающаяся четырех дуг. Т. к. она заключена между двумя концентрическими окружностями, то ее диаметр равен расстоянию между этими окружностями, т. е. b/2 и, следовательно, радиус равен b/4. А тогда становится ясным и положение ее центра.

В рассмотренном примере радиусы находились без всяких затруднений. В других аналогичных примерах могут потребоваться вычисления; покажем, как применяется в таких задачах теорема Пифагора.

В романской архитектуре часто встречается мотив, представленный на рисунке. Если b по-прежнему обозначает ширину окна, то радиусы полуокружностей будут равны R = b/2 и r= b/4. Радиус p внутренней окружности можно вычислить из прямоугольного треугольника, изображенного на рис. пунктиром. Гипотенуза этого треугольника, проходящая через точку касания окружностей, равна b/4 + p, один катет равен b/4, а другой b/2 - p. По теореме Пифагора имеем:

(b/4 + p) ² = (b/4)² + (b/2 - p)²

или b²/16 + bp/2 + p² = b²/16 +b²/4 - bp + p²,

откуда

bp/2 = b²/4 - bp.

Разделив на b и приводя подобные члены, получим:

(3/2)p = b/4, p = b/6

В конце девятнадцатого века высказывались разнообразные предположения о существовании обитателей Марса подобных человеку, это явилось следствием открытий итальянского астронома Скиапарелли (открыл на Марсе каналы которые долгое время считались исскуственными) и др.

Естественно, что вопрос о том, можно ли с помощью световых сигналов объясняться с этими гипотетическими существами, вызвал оживленную дискуссию. Парижской академией наук была даже установлена премия в 100000 франков тому, кто первый установит связь с каким-нибудь обитателем другого небесного тела; эта премия все еще ждет счастливца. В шутку, хотя и не совсем безосновательно , было решено передать обитателям Марса сигнал в виде теоремы Пифагора.

Неизвестно, как это сделать; но для всех очевидно, что математический факт, выражаемый теоремой Пифагора имеет место всюду и поэтому похожие на нас обитатели другого мира должны понять такой сигнал.

Значение теоремы Пифагора.

Кроме этого, практическое значение теоремы Пифагора и обратной ему теоремы заключается в том, что с их помощью можно найти длины отрезков, не измеряя самих отрезков. Это как бы открывает путь от прямой к плоскости, от плоскости к объемному пространству и дальше. Именно по этой причине теорема Пифагора так важна для человечества, которое стремится открывать все больше измерений и создавать технологии в этих измерениях. Например в Германии недавно открылся кинотеатр, где показывают кино в шести измерениях: первые три даже перечислять не стоит, а также время, запах и вкус. Это наглядно говорит о том, насколько быстро увеличивается количество измерений, используемых человечеством. Ведь еще три года назад никто и не заикался о более чем трех измерениях в кино. Вы спросите: а как связаны между собой теорема Пифагора и запахи, вкусы? А все очень "просто": ведь при показе кино надо рассчитать куда и какие запахи направлять и т.д. Представьте: на экране показывают джунгли, и вы чувствуете запах листьев, показывают обедающего человека, а вы чувствуете вкус еды...

Но не надо думать, что теорема Пифагора больше не имеет других значений. Из того, что я уже сказал, надо сделать вывод, что все эти технологии используются также и в других отраслях. Например, при строительстве любого сооружения, рассчитывают расстояния, центры тяжести, размещение опор, балок и т.д. В целом, значение теоремы, кроме вышесказанного, заключается в том, что она применяется практически во всех современных технологиях, а также открывает простор для создания и придумывания новых.

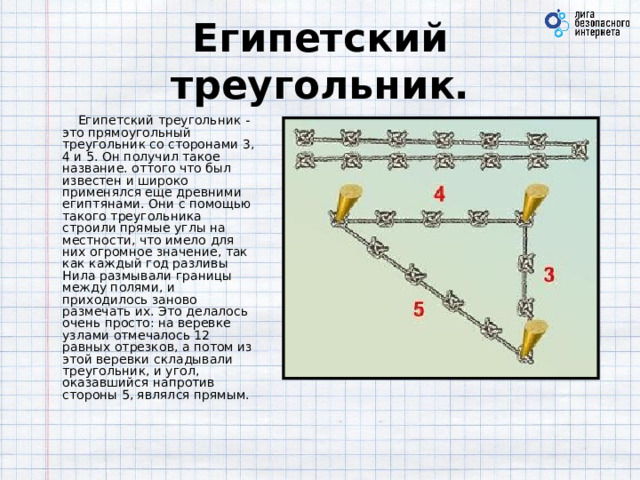
Египетский треугольник.

Египетский треугольник - это прямоугольный треугольник со сторонами 3, 4 и 5. Он получил такое название. оттого что был известен и широко применялся еще древними египтянами. Они с помощью такого треугольника строили прямые углы на местности, что имело для них огромное значение, так как каждый год разливы Нила размывали границы между полями, и приходилось заново размечать их. Это делалось очень просто: на веревке узлами отмечалось 12 равных отрезков, а потом из этой веревки складывали треугольник, и угол, оказавшийся напротив стороны 5, являлся прямым.

Исторические задачи .

Исторические задачи

Предлагаю несколько задач, найденных в исторических книгах. Они настолько легкие, что я не буду объяснять их решение.

Задача Бхаскари

«На берегу реки рос тополь одинокий. Вдруг ветра порыв его ствол надломал. Бедный тополь упал. И угол прямой С теченьем реки его ствол составлял. Запомни теперь, что в этом месте река В четыре лишь фута была широка Верхушка склонилась у края реки. Осталось три фута всего от ствола, Прошу тебя, скоро теперь мне скажи: У тополя как велика высота?»

Задача из китайской «Математики в девяти книгах»

«Имеется водоем со стороной в 1 чжан = 10 чи.

В центре его растет камыш, который выступает

над водой на 1 чи.

Если потянуть камыш к берегу, то

он как раз коснётся его.

Спрашивается: какова глубина воды и

какова длина камыша?».

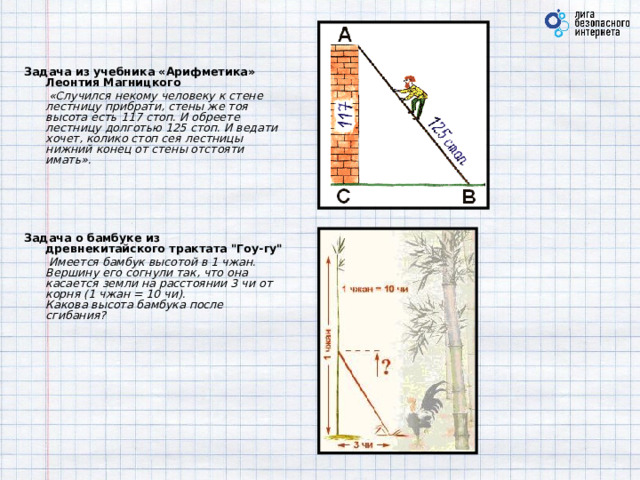
Задача из учебника «Арифметика» Леонтия Магницкого

«Случился некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать».

Задача о бамбуке из древнекитайского трактата "Гоу-гу"

Имеется бамбук высотой в 1 чжан. Вершину его согнули так, что она касается земли на расстоянии 3 чи от корня (1 чжан = 10 чи). Какова высота бамбука после сгибания?

Ни один человек ещё не научился думать, читая в готовом виде записанные мысли другого человека. Научиться думать можно, лишь размышляя самостоятельно.

Михай Эминеску

04/28/2024

81

04/28/2024

81

04/28/2024

81

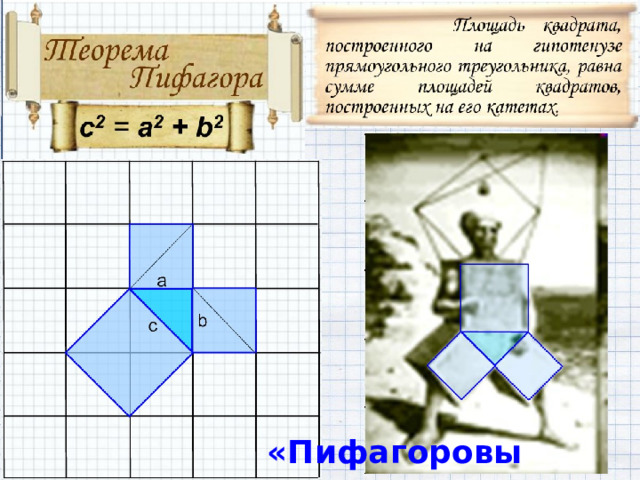
«Пифагоровы штаны»

04/28/2024

81

81

04/28/2024

81

04/28/2024

81

Пифагор Самосский

04/28/2024

81

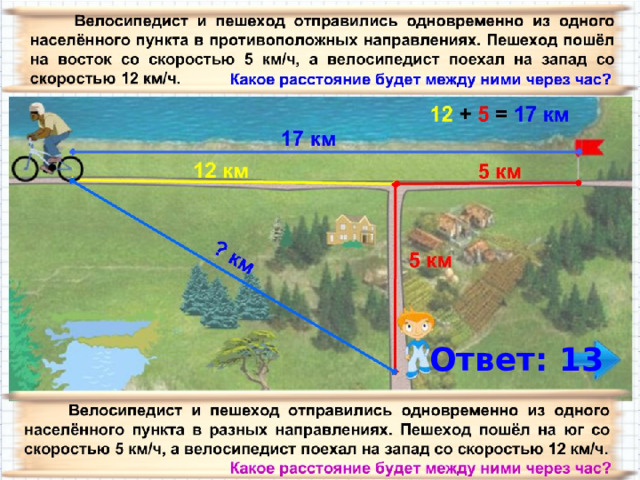
Ответ: 13

04/28/2024

81

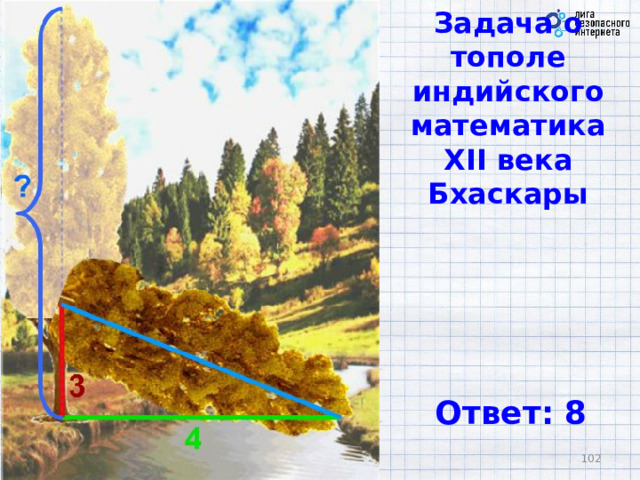
Задача о тополе

индийского математика

XII века Бхаскары

Ответ: 8

04/28/2024

81

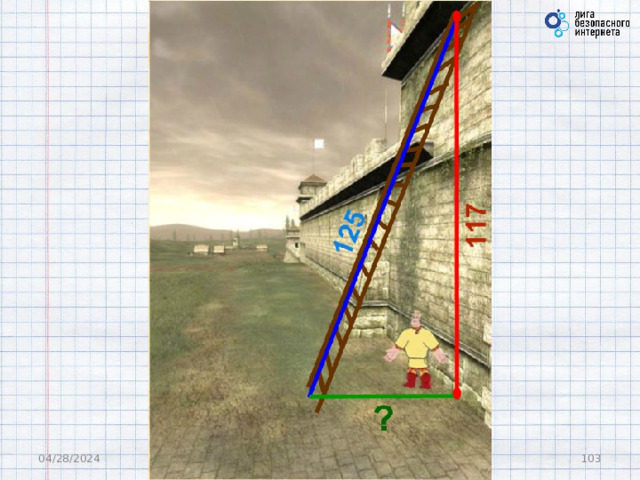
04/28/2024

81

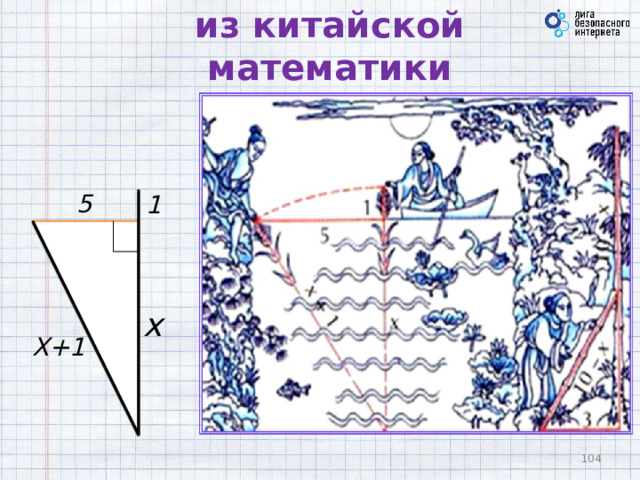
Задача о камыше

из китайской математики

5

1

x

X+1

81

Итоги урока

81

Высказывание Пифагора:

Из двух человек одинаковой силы сильнее тот, кто прав.

Спасибо за урок!

81