Методическая разработка урока по математике "Пирамида и её элементы" (СПО)

преподавателя

Деятельность

учащихся

Планирование

времени (мин.≈)

1

2

3

1.Организационный момент.

Цель: мотивирование студентов к учебной деятельности, создание благоприятного психологического настроя на работу (ОК1).

2

2. Постановка темы, целей урока.

Цель: создание условий для возникновения у обучающихся внутренней потребности включения в учебную деятельность (ОК 2).

3.Актуализация опорных знаний

Цель: организовать актуализацию умений и навыков (ОК1-ОК6).

На предыдущих занятиях мы с вами изучали многогранники, решали задачи. Сегодня повторим полученные знания, но на этом уроке рассмотрим многогранники с другой стороны – как геометрическое тело, которое очень часто встречается в выбранной вами профессии «Мастер общестроительных работ». Применим навыки вычисления площади поверхности и объема призмы при решении задач производственного содержания.

6

Вопросы по теме «Многогранники, площади их поверхностей и объёмы».

3.1.Какое тело называют многогранником?

Поверхность которого состоит из конечного числа плоских многоугольников.

3.2.Назовите виды многогранников.

Выпуклый, невыпуклый.

3.3.Назовите отличия выпуклого многогранника.

Выпуклый многогранник это тот многогранник, который расположен по одну сторону от плоскости любой его грани.

3.4. Перечислите виды многогранников, которые мы с вами изучили.

Пирамида, усеченная пирамида, прямоугольный параллелепипед, призма.

3.5. Какой многогранник называют призмой?

Призмой называется многогранник, который состоит из двух плоских многоугольников, лежащих в разных плоскостях и совмещаемые параллельным переносом, и всех отрезков, соединяющих точки этих многоугольников.

3.6.Назовите виды призм.

Прямая, наклонная, правильная.

3.7.Чемотличаются эти виды призм?

Прямая призма – боковые ребра призмы перпендикулярны основанию. Наклонная призма – боковые ребра призмы не перпендикулярны. Правильная призма – если в основании лежит правильный многоугольник.

3.8.Назовите элементы прямой призмы.

Высота призмы – его боковое ребро, длина - стороны основания.

3.9.Назовите формулу S полной и боковой поверхности призмы.

S_п.п.= 2S_о+S_б.п.; площадь полной поверхности равна сумме площадей боковой поверхности и удвоенной площади основания; S_б.п.=P·h, площадь боковой поверхности равна произведению периметра основания на высоту.

3.10.Как найти V призмы?

V=S_o·h, объём равен произведению площади основания на высоту.

3.11.Где в быту и на производственном обучении вы встречали призму?

Дом имеет форму прямоугольной четырехугольной призмы, шкаф, кирпичные стены, бетонные перемычки, фундаментные блоки, балки.

Вопросы по теме «Основы строительного материаловедения»

3.12. Какие строительные материалы в форме призмы или ее элементов чаще всего используются при возведении шатровых крыш и какие их свойства важны для обеспечения прочности и долговечности кровли?

Брус и доска: эти пиломатериалы в форме призмы используются для стропильной системы и обрешетки. Важны их прочность на изгиб и растяжение, влагостойкость (если они не обработаны антисептиками), а также правильная сушка для предотвращения деформаций;

Металлический профиль (уголок, профиль): используется в стропильной системе для усиления или создания сложных геометрических форм. Важна прочность на изгиб и коррозионная стойкость;

Кровельные материалы (металлочерепица, профнастил): хотя сами листы не являются призмами, их укладка и крепление к обрешетке формируют плоскости кровли, а расчет их необходимого количества основывается на площади поверхности пирамидальной формы. Важны их водонепроницаемость, устойчивость к атмосферным воздействиям, долговечность.

3.13. Предположим, что при расчете объема котлована в форме усеченной пирамиды вы получили значение 200 м³. Какие факторы, связанные со свойствами грунта, могут повлиять на фактическое количество вывозимого грунта и стоимость работ?

Плотность, влажность, состав и разбухание грунта.

3.14. Для возведения кирпичной колонны в форме правильной призмы необходимо рассчитать количество кирпича. Какие характеристики кирпича (как строительного материала) и призматической формы колонны необходимо учитывать для точного расчета?

Размеры кирпича, размеры колонны, плотность кирпича, вид кирпича, толщина шва и вид перевязки кладки.

4. Изучение нового материала

Цель: дать определение пирамиды и её элементов, используя профессиональную терминологию (основание, высота, боковые грани, апофема, рёбра), познакомить с видами пирамид, акцентируя внимание на примерах из строительной практики (шатровые крыши, купольные конструкции).

20

4.1. Определение «Пирамида»

Пирамидой называется многогранник, который состоит из плоского многоугольника — основания пирамиды, точки, не лежащей в плоскости основания, — вершины пирамиды и всех отрезков, соединяющих вершину пирамиды с точками основания. (представьте, что у вас есть многоугольник (треугольник, четырёхугольник, пятиугольник и т. д.). Теперь возьмите точку вне плоскости этого многоугольника и соедините эту точку отрезками со всеми вершинами многоугольника. Полученная фигура — это и есть пирамида. Многоугольник — это её основание, а образовавшиеся треугольники — это её боковые грани)

4.2. Основание пирамиды

Основание пирамиды — это многоугольник, который не является боковой гранью. (Основание — это плоская фигура (многоугольник). Именно по форме основания различают пирамиды (треугольные, четырёхугольные и т. д.))

4.3. Боковые грани

Боковые грани - треугольные грани, сходящиеся в вершине. (Каждая боковая грань «опирается» на одну сторону основания пирамиды)

4.4. Вершина пирамиды

Вершина пирамиды — общая точка боковых граней, не лежащая в плоскости основания. (Вершина — это «верхняя» точка пирамиды, где сходятся все боковые грани. Она не лежит в плоскости основания пирамиды.)

4.5. Боковые ребра пирамиды

Боковые ребра пирамиды — это отрезки, соединяющие вершину пирамиды с вершинами основания. (Боковые рёбра — это «линии», по которым боковые грани «соединяются» между собой. Это отрезки, которые идут от вершины пирамиды к углам основания.)

4.6. Высота пирамиды

Высота пирамиды — это перпендикуляр, опущенный из вершины пирамиды на плоскость ее основания. (Высота — это кратчайший путь от вершины пирамиды к ее основанию. Она перпендикулярна (образует прямой угол) плоскости основания. В строительстве высота пирамиды (например, крыши) важна для расчета объемов и углов наклона.)

4.7. Апофема

Апофема — это высота боковой грани правильной пирамиды, проведенная из ее вершины. (Апофема — это отрезок, проведенный из вершины пирамиды к середине стороны основания по боковой грани. Она является высотой боковой грани и часто используется для вычисления площади поверхности правильной пирамиды.)

4.8. Виды пирамид по форме основания

Пирамиды различаются по форме многоугольника, лежащего в основании. Самые распространенные виды:

треугольная пирамида (тетраэдр): основанием является треугольник

четырехугольная пирамида: основанием является четырёхугольник (квадрат, прямоугольник, параллелограмм и т. д.)

пятиугольная пирамида: основанием является пятиугольник и т.д.

4.9. Правильная пирамида

Правильная пирамида — это пирамида, основанием которой является правильный многоугольник, а высота пирамиды опускается в центр этого многоугольника. (Правильная пирамида — это особый вид пирамиды, основание которой представляет собой правильную фигуру (все стороны и углы равны). Высота таких пирамид всегда направлена в центр основания. В строительстве шатровые крыши часто имеют форму правильной пирамиды.)

4.10. Площадь боковой поверхности пирамиды

Площадь боковой поверхности пирамиды — это сумма площадей всех ее боковых граней. (В правильной пирамиде все боковые грани равны, и площадь боковой поверхности вычисляется проще. В строительстве эти знания нужны, например для расчёта количества материала для облицовки пирамидальных конструкций.)

Площадь боковой поверхности правильной пирамиды равна: Sбок=121/2*Ра, где Р — периметр основания, а — апофема (Площадь боковой поверхности правильной усечённой пирамиды равна произведению полусуммы периметров оснований на апофему)

4.11. Площадь полной поверхности пирамиды

Площадь полной поверхности пирамиды - называется сумма площадей всех её граней (основания и боковых граней) Sполн=Sбок+Sосн.

4.12. Объем пирамиды

Объем пирамиды вычисляется по формуле: V = (1/3) * Sосн * h, где Sосн — площадь основания, а h — высота пирамиды.

5. Формирование практических навыков и навыков умственного труда

10

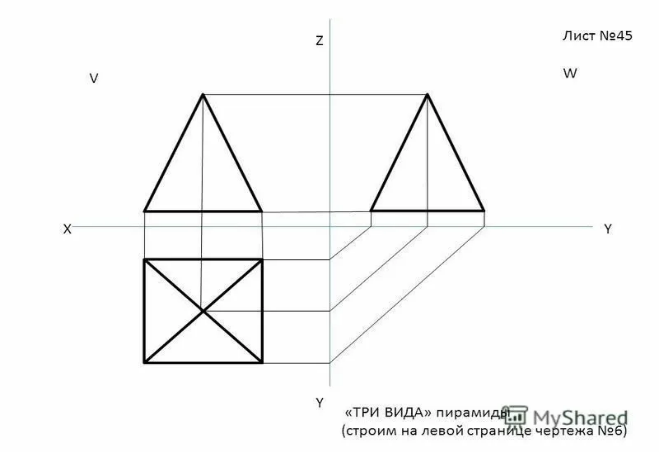
5.1. Даны линейные размеры пирамиды (например, высота 5 метров, основание — квадрат со стороной 4 метра. Задание: выполните простейший чертёж этой пирамиды в виде сверху и сбоку (без учёта масштаба, схематично, главное — соблюсти форму и основные элементы).

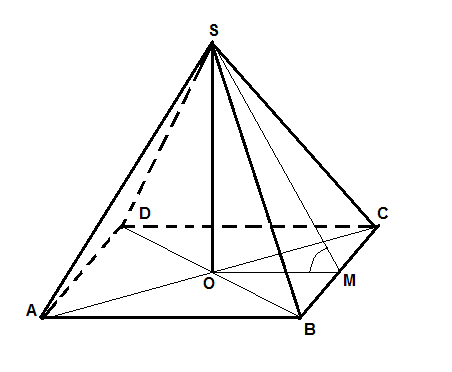
5.2. Крыша имеет форму правильной четырехугольной пирамиды. Угол между боковой гранью пирамиды и основанием равен 45 гр. Длина основания крыши 4,5 м. Сколько металлических листов понадобиться, чтобы покрыть крышу, если размеры листа 70 см на 140 см. (необходимый резерв материала 10% от площади крыши).

Пирамида ABCDS, в оcновании лежит квадрат ABCD, AB = BC = CD = AD = 4,5 м.
O – центр квадрата, M – середина BC, угол SMO = 45°.
Размер мет. листа 140х70 см. Необходимый резерв равен 10% от площади крыши.
Сколько надо листов, чтобы покрыть крышу?
Решение.
Найдем площадь боковой поверхности крыши.
OM = AB/2 = 4,5/2 = 2,25 м.
Угол SMO = 45°, значит, треугольник SMO – прямоугольный и равнобедренный.
Поэтому высота SO = OM = 2,25 м. а апофема SM = 2,25·√2 ≈ 3,18 м
Площадь одной боковой грани:
S(гр) = a·h/2 = BC·SM/2 = 4,5·3,18/2 ≈ 7,16 м²
Всего граней 4, общая площадь крыши:
S = 4·S(гр) = 4·7,16 = 28,64 м²
Добавляем 10% необходимого резерва:
S(R) = S + 0,1·S = 28,64 + 2,864 = 31,504 м²
Площадь 1 мет. листа S(л) = 140·70 см² = 1,4·0,7 м² = 0,98 м²
На всю крышу вместе с резервом нужно:
S(R)/S(л) = 31,504/0,98 = 32,147 = 33 листа.
Ответ: 33 листа.

Учащиеся самостоятельно решают задачу в тетрадях.

5

5.3. Возможно, кому-нибудь из вас придется решать такую или аналогичную задачу в дальнейшем, ведь математика очень тесно связана с выбранной Вами профессией.

Закрепление и обобщение материала.

6. Подведение итогов урока. Рефлексия.

Цель: дать качественную оценку работы группы и наиболее активных обучающихся. Сформировать рефлексивную самооценку деятельности на уроке (ОК-8).

5

Подобные измерения, расчеты и вычисления вы будете выполнять в своих выпускных экзаменационных работах.

А теперь давайте вернемся к листам настроения и оценим свое участие в уроке.

Учащиеся оценивают свое настроение (прил.1).

Учитель комментирует общее настроение. Оценивает ответы учащихся.

7. Домашнее задание. Постановка дальнейшей перспективы

2

Математика — это тот предмет, который тесно связан с изучением таких дисциплин как: основы строительного черчение, основы строительного материаловедения, производственная практика, необходимых для овладения вашей будущей профессией «Мастер общестроительных работ».

Домашнее задание: выполните чертёж (вид сверху и вид сбоку) строительной конструкции, имеющей пирамидальную форму. Это может быть: шатровая крыша, купол, пирамидальный навес, декоративный элемент фасада. Укажите все размеры (длину, высоту), используя профессиональные обозначения (h, l, a и т. д.). Используйте линейку, карандаш, ластик, соблюдайте точность.