Методические рекомендации по изучению темы "Решение задач на нахождение элементов призмы"

Занятие 96. Тема «Решение задач на нахождение элементов призмы»

План занятия:

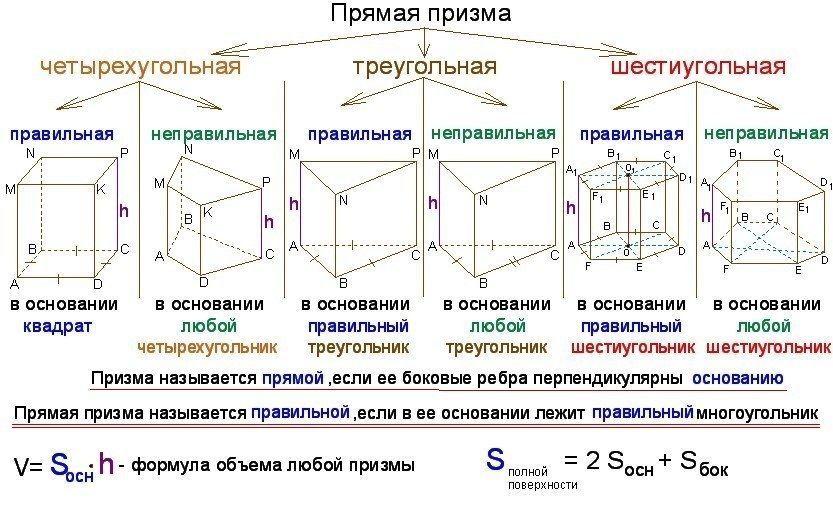
1. Повторить понятие призмы, прямой призмы, правильно й призмы.

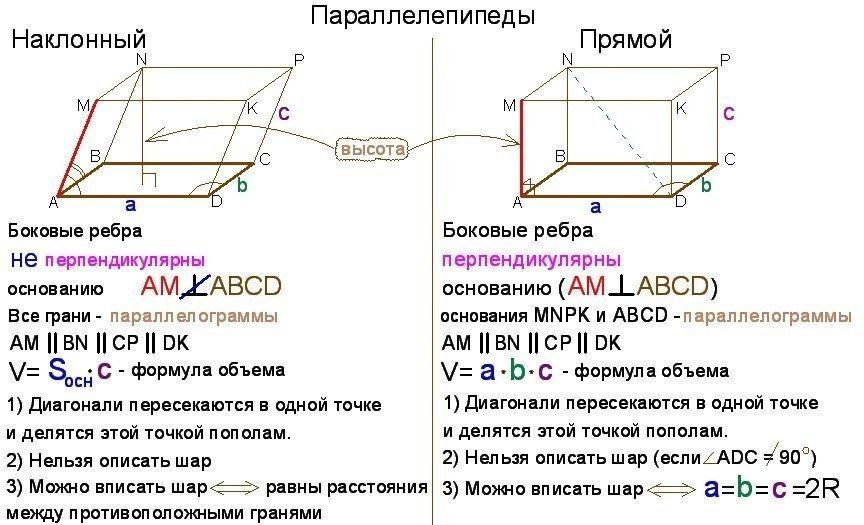
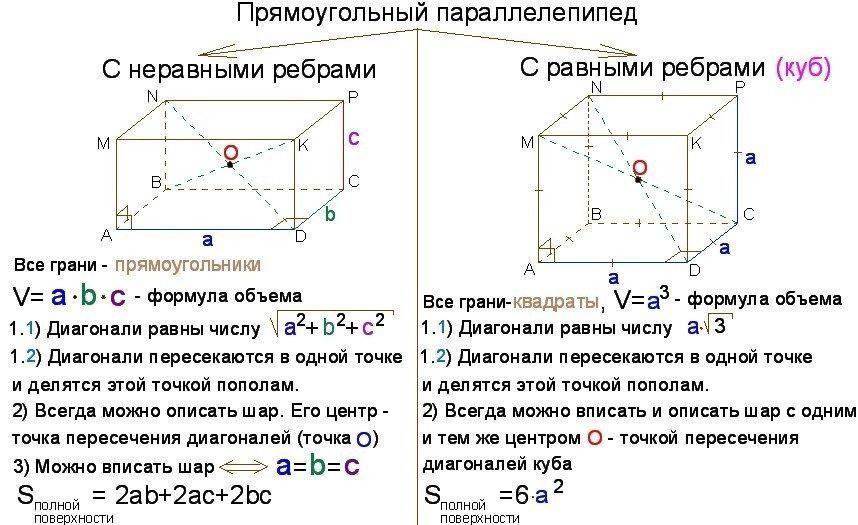
2. Повторить понятие параллелепипеда, прямоугольного параллелепипеда.

3. Повторить формулы для вычисления площади поверхности призмы.

Решить задачу:

1. Основанием прямой треугольной призмы является прямоугольный треугольник с катетами 5 см и 12 см. Площадь большей боковой грани равна 104 см². Вычисли те высоту призмы.

1. В прямоугольном параллелепипеде стороны основания равны 12 см и 5 см. Диагональ параллелепипеда образует с плоскостью основания угол в 45⁰. Найдите боковое ребро параллелепипеда.

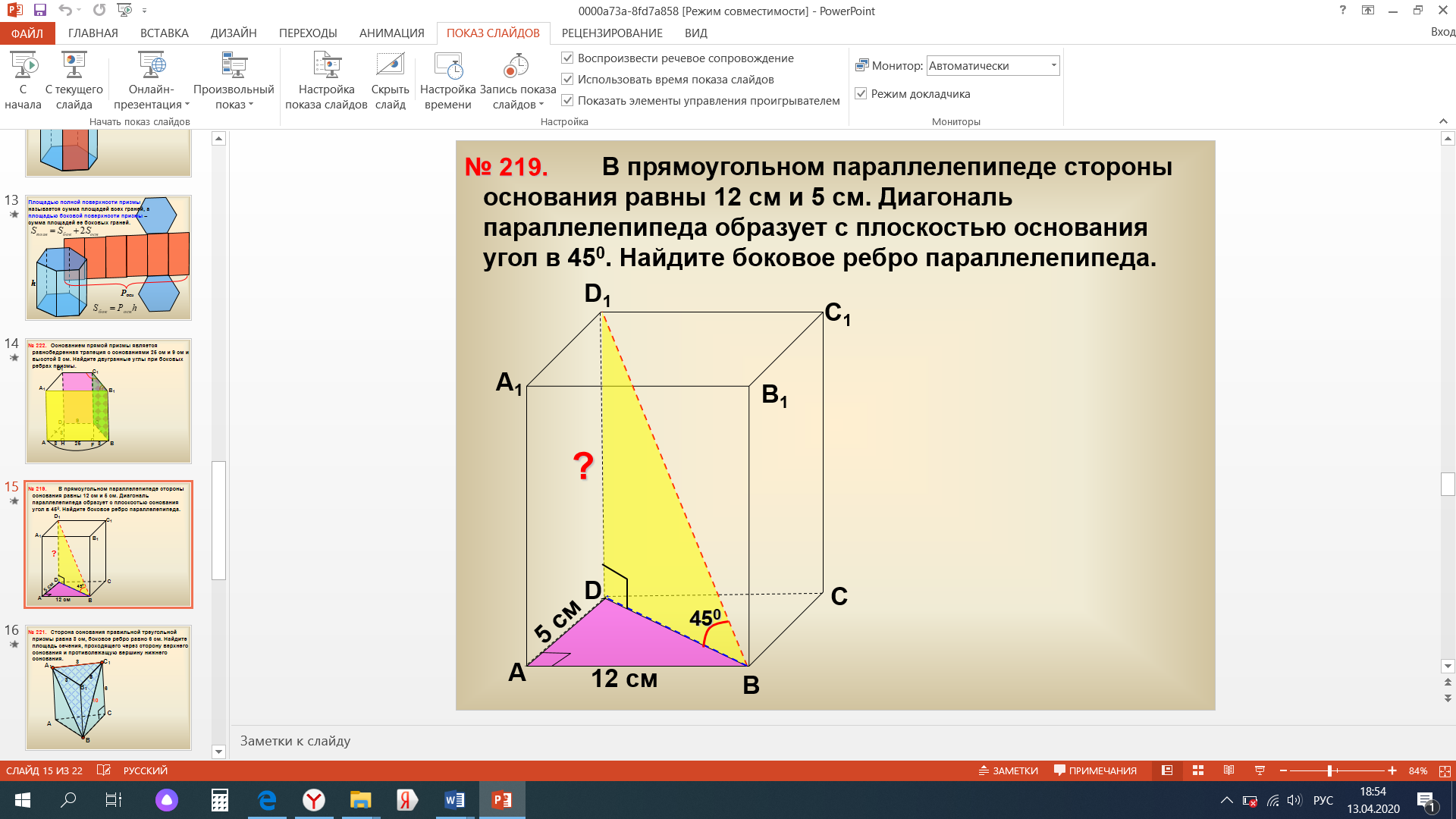
Искомым боковым ребром являются ребра: DD₁, BB₁, CC₁, AA₁. Т.к. параллелепипед прямоугольный, то все боковые ребра равны. Найдем DD_1. Искомый отрезок DD_1, очевидно будем находить из треугольника ВDD_1. Данный треугольник прямоугольный, угол D равен 90⁰. Кроме этого треугольник является равнобедренным, т.к. один из углов равен 45⁰. Следовательно, DD₁= DB. Отрезок DB найдем из прямоугольного треугольника АDB, в котором он является гипотенузой. По теореме Пифагора

DD₁= DB=13 см.

Ответ: DD₁=13 см.

1. Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 15, а площадь полной поверхности равна 930.

В основании правильной четырехугольной призмы – квадрат и боковое ребро призмы перпендикулярно основанию.

Площадь полной поверхности правильной четырехугольной призмы состоит из двух площадей основания (площадей квадратов) и четырех площадей боковых граней (площадей прямоугольников)

 , где  H – длина бокового ребра призмы.

480=60 H

H=8 см.

Ответ: 8. 

1. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 25 и 60, и боковым ребром, равным 25.

Задание для самостоятельного выполнения

Учебник «Геометрия 10-11 класс», А.В. Погорелов, размещен на сайте

Задание 1. Сделать краткий конспект по данной теме.

Задание 2. Выучить все формулировки определений и теорем.

Задание 3. Решить задачи: №10 стр. 83, №17 стр. 84, №33 стр. 85.

Выполненные задания и вопросы по выполнению работ отправить на адрес электронной почты преподавателя: [email protected]. Имя файла – фамилия студента и номер занятия. (например, Петров-96)

ВНИМАНИЕ! С 20.04 оценка будет выставляться одна за два занятия (на первом занятии изучается новая тема, составляется конспект (ставится зачет по конспекту), на втором занятии решаются задачи по новой теме. Задачи, списанные друг у друга или с интернета не оцениваются. Работы необходимо присылать до 15³⁰ (т.к. есть категория студентов, присылающих работы ночью. Оценки за несвоевременно выполненные задания без уважительной причины будут снижены).