Просмотр содержимого документа
«Методические рекомендации по выполнению практической работы по теме:"Вычисление производной"»
3
Практическая работа
Определение производной. Простейшие правила вычисления производных.
Основные понятия:
Приращение функции.
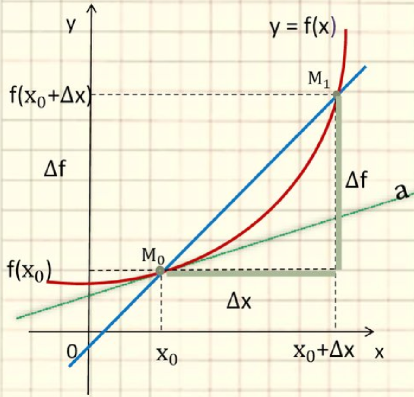
Рассмотрим функцию 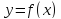 .
. 
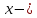 независимая переменная, аргумент.
независимая переменная, аргумент.
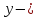 зависимая переменная, функция.
зависимая переменная, функция.
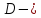 область определения функции.
область определения функции.
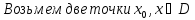
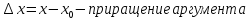
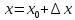 – переменная
– переменная 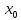 получила приращение
получила приращение 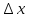
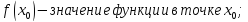
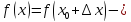 значение функции в точке
значение функции в точке 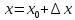
При изменении аргумента функция также изменяется, т.е. получает приращение:
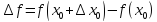 – приращение функции.
– приращение функции.
Определение производной функции.
Производной функции 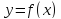 в точке
в точке 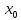 называется предел отношения приращения функции
называется предел отношения приращения функции 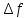 в точке
в точке 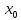 к приращению аргумента
к приращению аргумента 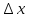 в этой же точке, когда приращение аргумента в этой точке стремится к нулю.
в этой же точке, когда приращение аргумента в этой точке стремится к нулю.
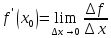
или
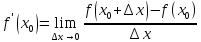
Если функция имеет в некоторой точке производную, то она называется дифференцируемой в этой точке.
Пусть 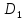 - множество точек в которых функция
- множество точек в которых функция 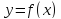 дифференцируема. Сопоставляя каждому числу
дифференцируема. Сопоставляя каждому числу 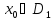 число
число 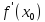 , получим функцию, определенную на множестве
, получим функцию, определенную на множестве 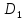 . Эта функция называется производной функцией данной функции
. Эта функция называется производной функцией данной функции 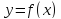 и обозначается
и обозначается  .
.
Нахождение производной данной функции называется дифференцированием.
Правила вычисления производных.
Если функции  и
и  дифференцируемы в точке
дифференцируемы в точке 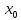 , c – постоянная величина, то выполняются следующие свойства:
, c – постоянная величина, то выполняются следующие свойства:




Производные некоторых элементарных функций:
Производная сложной функции.
Рассмотрим функцию . Это сложная функция. Представляет собой композицию функций  и
и  .
.
Т.е. 
Производную сложной функции  вычисляют по правилу:
вычисляют по правилу:
.
Например.Продифференцируем функцию
.
Задания. Пример выполнения практической работы.
Задание 1. Найдите производную по определению производной.
| а) | 
| Находим значение функции в точке 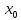  Находим значение функции в точке 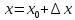 ; Находим приращение функции 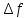 в точке в точке 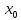 : : Находим производную функции 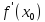 : :
|
|
| б) | 
| Самостоятельно дома |
| в) | 
| Находим значение функции в точке 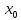  Находим значение функции в точке 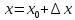 ; Находим приращение функции 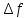 в точке в точке 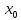 : : Находим производную функции 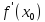 : :
|
| г) | 
| Самостоятельно дома |
| д) | 
| Находим значение функции в точке 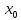 Находим значение функции в точке 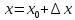 ; Находим приращение функции 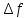 в точке в точке 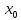 : :
Находим производную функции 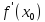 : :
|
| е) | 
| Самостоятельно дома |
Задание 2. Найдите производные следующих функций.
| а) | 
| 
|
| б) | 
| 
|
| в) | 
| 
|
| г) | 
| 
|
| д) | 
| ; |
| е) | |
|
| ж) | 
| |
| з) | 
| |
Задание 3.
| а) | 
| |
| б) | | |
| в) | 
| |
| г) | 
| Самостоятельно дома |
| д) | 
| Самостоятельно дома |
Задание 4.
| а) | 
| |
| б) | 
| Самостоятельно дома |
| в) | 
| |
| г) | 
| Самостоятельно дома |
| д) | 
| |
| е) | 
| |
Задание 5.
| а) | 
| |
| б) | 
| |
| в) | 
| ; |
| г) | 
| Самостоятельно дома |
| д) | 
| |
Задание 6.
| а) | 
| ; |
| б) | 
| |
| в) | 
| |
| г) | 
| Самостоятельно дома |
| д) | 
| |
| е) | 
| Самостоятельно дома |
| ж) | 
| |
| з) | 
| |
| и) | 
| |
| к) | 
| |
| л) | 
| |
| м) | 
| Самостоятельно дома |
| н) | 
| Самостоятельно дома |
Задание 7.
| а) | 
| |
| б) | 
| |
| в) | 
| |
| г) | 
| |
| д) | 
| |
| е) | 
| Самостоятельно дома |
| ж) | 
| |
| з) | 
| |
| и) | 
| .
|






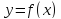 .
. 
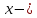 независимая переменная, аргумент.
независимая переменная, аргумент.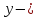 зависимая переменная, функция.
зависимая переменная, функция.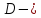 область определения функции.
область определения функции. 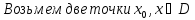
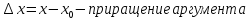
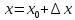 – переменная
– переменная 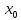 получила приращение
получила приращение 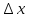
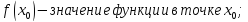
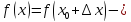 значение функции в точке
значение функции в точке 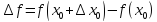 – приращение функции.
– приращение функции.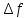 в точке
в точке 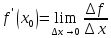
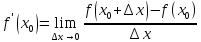
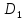 - множество точек в которых функция
- множество точек в которых функция 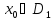 число
число 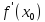 , получим функцию, определенную на множестве
, получим функцию, определенную на множестве 









