Министерство образования Пензенской области
ГАПОУ ПО «Кузнецкий колледж электронных технологий»
Методические рекомендации
практического занятия
по учебной дисциплине
ЕН. 01 Математика
на тему: «Матрицы. Действия над матрицами»
Кузнецк 2019
Пояснительная записка.
Методические рекомендации к практическому занятию по учебной дисциплине ЕН.01 Математика на тему «Матрицы. Действия над матрицами» предназначено для студентов 2 курса специальности 13.02.01 «Техническое обслуживание электрического и электромеханического оборудования». Рекомендации содержат теоретический материал и примеры выполнения, что позволяет студентам легко выполнить все поставленные задачи.
Выполнение практического занятия направлено на обобщение, систематизацию, углубление теоретических знаний учебной дисциплины; формирование умений применять полученные знания в практической деятельности; на развитие аналитических, проектировочных, конструктивных умений; выработку самостоятельности, ответственности и творческой инициативы.
Для выполнения работы, студент обязан знать:
- определение матрицы;
- основные понятия матрицы;
- действия над матрицами.
Уметь:
- применять полученные знания на сложение, вычитание и произведение матриц;
- верно производить арифметические расчеты.
Тема: Матрицы. Операции над матрицами.
Цель: сформировать умение выполнять основные операции над матрицами.
Теоретические сведения к практической работе
Определение. Матрицей размером nm называется прямоугольная таблица, составленная из n m чисел и имеющая n строк и m столбцов. Числа ij, составляющие матрицу, называются элементами матрицы
А=(ij)= 
Определение. Матрицу Аt называют транспонированной по отношению к матрице А, если она получена из матрицы А заменой строк этой матрицы её столбцами, и, наоборот, столбцов строками.
 .
.
Пример,  ,
,  .
.
Определение. Квадратная матрица называется треугольной, если все ее элементы, размещенные над главной диагональю (под ней), равны нулю, т.е.
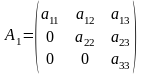 - верхняя треугольная матрица,
- верхняя треугольная матрица,
 – нижняя треугольная матрица.
– нижняя треугольная матрица.
Определение. Матрица, все элементы которой равны нулю, называется нуль-матрицей.
Матрица-строка  , матрица-столбец
, матрица-столбец  .
.
Операции над матрицами.
1) Пусть матрицы  и
и  одинаковой размерности. Суммой матриц
одинаковой размерности. Суммой матриц  и
и  называется матрица
называется матрица  той же размерности, каждый элемент которой равен сумме соответствующих элементов матрицы
той же размерности, каждый элемент которой равен сумме соответствующих элементов матрицы  и
и  .
.
 для всех
для всех  и
и  .
.
2) Разностью матриц  и
и  одинаковой размерности называется матрица
одинаковой размерности называется матрица  той же размерности, каждый элемент которой рамен разности соответствующих элементов матрицы
той же размерности, каждый элемент которой рамен разности соответствующих элементов матрицы  и
и  .
.
 для всех
для всех  и
и  .
.
3) Произведением матриц  на число
на число  называется матрица
называется матрица  , каждый элемент которой равен
, каждый элемент которой равен  .
.
4) Матрицу  можно умножить на матрицу
можно умножить на матрицу  (
( ) лишь в то случае, когда число столбцов первой матрицы
) лишь в то случае, когда число столбцов первой матрицы  равно число строк второй матрицы
равно число строк второй матрицы  , т.е.
, т.е.  . При этом каждый элемент матрицы-произведения
. При этом каждый элемент матрицы-произведения  определяется так:
определяется так:
, для всех  и
и  .
.
Т.е., элемент  равен сумме произведений элементов
равен сумме произведений элементов  -й строки матрицы
-й строки матрицы  на соответствующие элементы
на соответствующие элементы  -го столбца матрицы
-го столбца матрицы  .
.
Найти произведение матрицы-строки и матрицы-столбца:
Пример 1.
1) ,
2) ,
3) ,
4) ,
5) .
Пример 2
Для заданных матриц  ,
,  ,
,  найти матрицы
найти матрицы  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
, , .
Решение
1.1)
;
1.2) ;
1.3)
;
1.4)
;
1.5)
.
Подчеркнем еще раз, что  .
.
1.6)
;
Содержание практической работы:
Задание 1. Для матриц  ,
,  ,
,  вычислить:
вычислить:
1)  , 2)
, 2)  , 3)
, 3)  ,
,
4)  , 5)
, 5)  , 6)
, 6)  , если
, если
, , .
Задание 2. Для матриц  ,
,  ,
,  вычислить:
вычислить:
1)  , 2)
, 2)  ,
,
3)  , 4)
, 4)  , если
, если
, , .
Задание 3. Найти произведение матриц:
1) ; 2)  ;
;
3) ; 4) ;
5) ; 6) ;
7) ; 8)
Ссылки на используемые источники:
https://multiurok.ru/files/metodicheskie-rekomendatsii-prakticheskogo-zaniati.html?login=ok
https://nsportal.ru/npo-spo/estestvennye-nauki/library/2018/10/23/prakticheskoe-rabota-po-matematike-po-teme-matritsy








 .
. ,
,  .
. 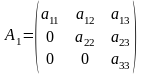 - верхняя треугольная матрица,
- верхняя треугольная матрица, – нижняя треугольная матрица.
– нижняя треугольная матрица. , матрица-столбец
, матрица-столбец  .
. и
и  одинаковой размерности. Суммой матриц
одинаковой размерности. Суммой матриц  и
и  называется матрица
называется матрица  той же размерности, каждый элемент которой равен сумме соответствующих элементов матрицы
той же размерности, каждый элемент которой равен сумме соответствующих элементов матрицы  для всех
для всех  и
и  .
. для всех
для всех 









