Методические советы при подготовке школьников к выполнению задания 22 ОГЭ по математике
(Слайд №1)
Задание 22 ОГЭ по математике (2022).
Задание 22 ОГЭ па математике – задание высокого уровня сложности. Для его выполнения от выпускников основной школы требуется свободное владение изученным материалом раздела «Функции и их графики». Это задание рассчитано на обучающихся, изучающих математику основательно (углубленно). Выполнение этих заданий предполагает наличие у обучающегося исследовательских навыков, владения специальными приемами преобразования выражений, умений строить графики функций с помощью преобразований (параллельного переноса, симметрий и деформаций) и т.п.
Требования к выполнению этого задания такие же, как и к прочим задания с развернутым ответом. Решение должно быть математически грамотным, полным, лаконичным. В этом случае оно оценивается 2 баллами. Если в решении допущена вычислительная ошибка, погрешность в терминологии или символике, не влияющая на правильность общего хода решения (даже при неверном ответе) и позволяющая сделать вывод о владении материалом, то задание оценивается 1 баллом. При невыполнении предыдущих требований, решение задания 22 оценивается 0 баллов.
(Слайд №2) При выполнении задания 22 рекомендуется придерживаться следующего алгоритма:
-
преобразование формулы, задающей функцию, и нахождение области ее определения;
-
определение вида и характерных точек графика на каждом промежутке области определения;
-
изображение графика функции на координатной плоскости;
-
исследование графика функции в соответствии с вопросом к заданию;
-
запись ответа.
В ходе подготовки к ГИА для выполнения заданий №11 организуется повторение изученных в основной школе элементарных функций, их графиков и способов построения. Эти знания, конечно же, необходимы и для успешного выполнения.
Подготовка к выполнению заданий 22 проводится, в основном, на консультациях, т.к. в урочное время на эти задания времени, как правило, не достает.
При выполнении этого задания впервые и на нескольких последующих занятиях используем программу ГИС GeoGebra для того, чтобы ученик мог понять суть задания.
В дальнейшем GeoGebra применяется для проверки полученных результатов.
Приведем примеры выполнения задания 22 с использованием ГИС GeoGebra. (Слайд №3)
Пример 1
Постройте график функции 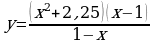 и определите, при каких значениях k прямая
и определите, при каких значениях k прямая  имеет с графиком ровно одну общую точку.
имеет с графиком ровно одну общую точку.
Действуем по приведенному приведённому выше алгоритму.
Преобразуем формулу, задающую функцию, и найдем область ее определения. Для преобразования формулы воспользуемся тождеством 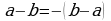 .
.
(Слайд №4) Формула, задающая функцию, представлена в виде дроби, знаменатель которой не может принимать нулевое значение. Значит, в область определения не входит аргумент, обращающий знаменатель в 0, т.е.  . Таким образом, область определения функции
. Таким образом, область определения функции 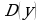 – все числа, кроме 1.
– все числа, кроме 1.
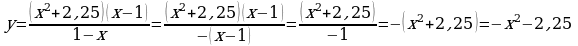
В программе GeoGebra строим график  в виде пунктирной прямой, подразумевая тем самым, что все ее точки не принадлежат графику исследуемой функции.
в виде пунктирной прямой, подразумевая тем самым, что все ее точки не принадлежат графику исследуемой функции.
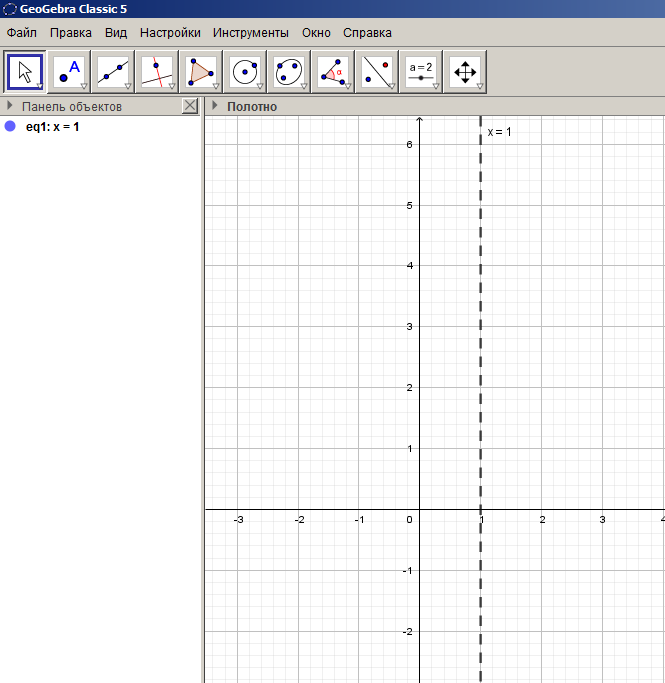
Выполняем второй шаг алгоритма (определение вида и характерных точек графика на каждом промежутке области определения).
Преобразованная формула заданной функции имеет вид:  . По ее виду определяем, что графиком функции является парабола, ветви которой направлены вниз (
. По ее виду определяем, что графиком функции является парабола, ветви которой направлены вниз (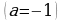 , вершина находится в точке
, вершина находится в точке 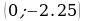 , т.к.
, т.к.  . Этой параболе не принадлежит точка
. Этой параболе не принадлежит точка 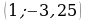 , так как
, так как  не входит в область определения функции, и
не входит в область определения функции, и 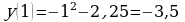 . График функции
. График функции  может быть получен из известного графика функции
может быть получен из известного графика функции  путем параллельного переноса на
путем параллельного переноса на  единичных отрезков вниз (или на вектор
единичных отрезков вниз (или на вектор  ).
).
Шаг 3 (изображение графика функции на координатной плоскости). Демонстрируем эти действия на координатной плоскости (обучающиеся сначала выполняют построения в тетради, затем в GeoGebra) (Слайд №5).
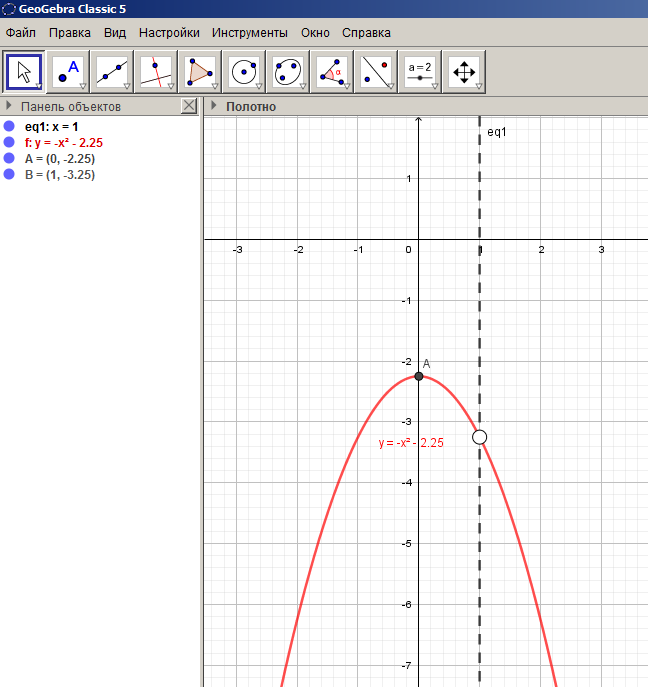
Шаг 4 (исследование графика функции в соответствии с вопросом к заданию).
Чтобы прямая  имела с построенным графиком одну общую точку, нужно чтобы или прямая
имела с построенным графиком одну общую точку, нужно чтобы или прямая  была касательной к графику
была касательной к графику  (и точка касания не равна 1), или прямая
(и точка касания не равна 1), или прямая  пересекает график
пересекает график  в точке
в точке  и в какой-то второй точке.
и в какой-то второй точке.
Случай касания реализуется, когда дискриминант квадратного уравнения 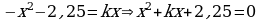 .
. 
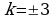 .
.
При этом, если  , точка касания
, точка касания 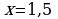 , а если
, а если 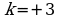 , точка касания
, точка касания 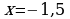 .
.
Для рассмотрения второго случая подставим  в уравнение
в уравнение 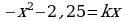 . Получим
. Получим 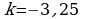 . При этом дискриминант этого уравнения будет больше нуля, значит, еще одно решение точно есть (Слайд №6).
. При этом дискриминант этого уравнения будет больше нуля, значит, еще одно решение точно есть (Слайд №6).
После получения результатов аналитическим путем продемонстрируем их с помощью ИГС.
Строим график прямой пропорциональности с  . Для задания разных значений параметра
. Для задания разных значений параметра 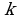 создадим ползунок, с помощью которого будем менять значения параметра, и наблюдать взаимное расположение прямой и параболы (Слайд №7).
создадим ползунок, с помощью которого будем менять значения параметра, и наблюдать взаимное расположение прямой и параболы (Слайд №7).
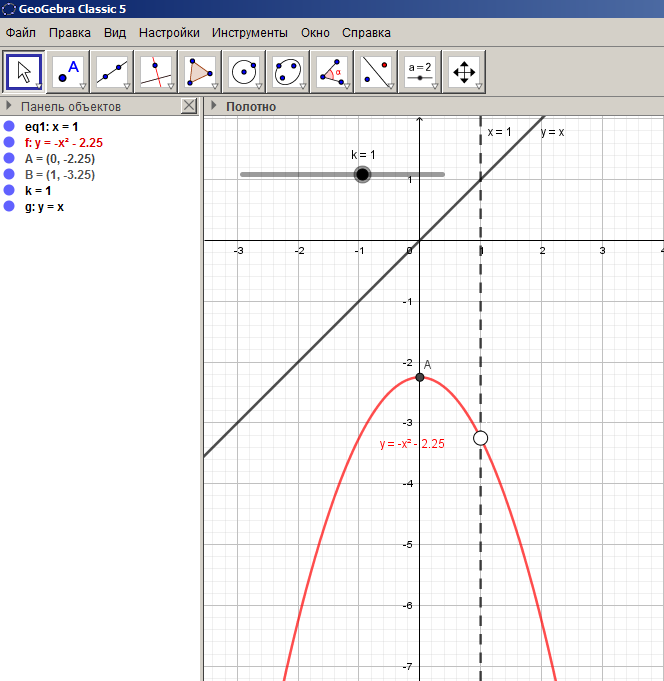
Далее меняем значения параметра, и наблюдаем за взаимным расположением прямой и параболы (Слайд №8) . В тот момент, когда параметр 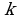 достигает значения
достигает значения 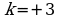 , прямая касается параболы, т.е. графики имеют одну общую точку (Слайд №9) .
, прямая касается параболы, т.е. графики имеют одну общую точку (Слайд №9) .
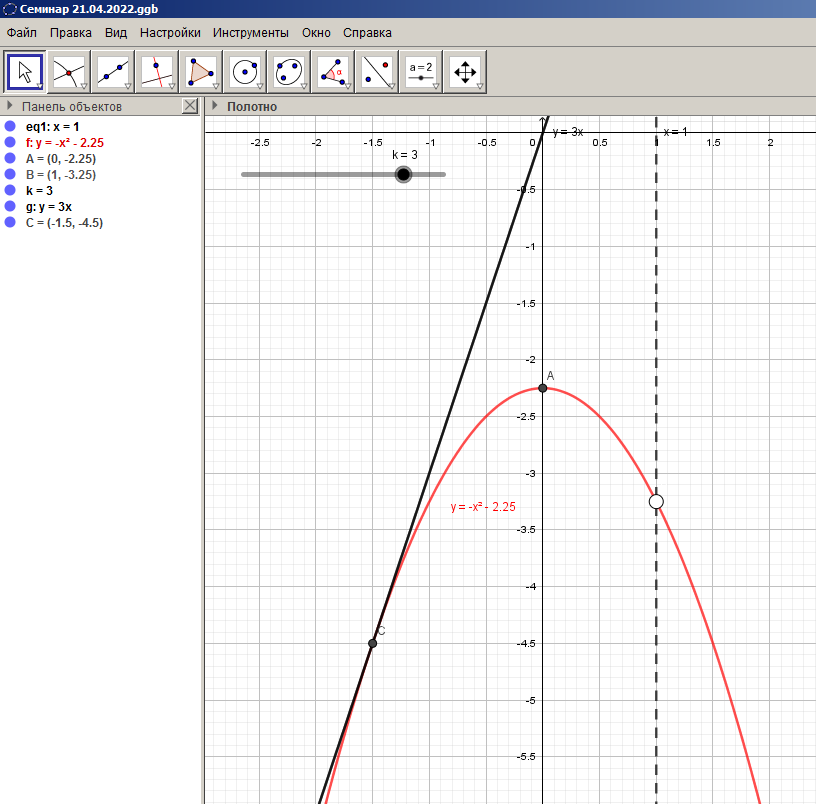
Когда параметр 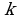 достигает значения
достигает значения  , прямая вновь касается параболы, т.е. графики имеют одну общую точку (Слайд №10) .
, прямая вновь касается параболы, т.е. графики имеют одну общую точку (Слайд №10) .

В тот момент, когда аргумент принимает значение равное единице ( ),
), 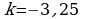 , прямая с параболой имеют одну общую точку (Слайд №11) .
, прямая с параболой имеют одну общую точку (Слайд №11) .

Пятый шаг (запись ответа). Ответ записываем традиционным образом, предварительно прочитав еще раз вопрос задания. Ответ:  .
.
Наглядная демонстрация поиска ответа на вопрос задания приводит к полному пониманию зависимости значений коэффициентов в формуле, задающей функцию, и расположения графика на координатной плоскости, а также того, что от обучающегося требуется в конкретном задании. С моей точки зрения, параллельное решение задания аналитическим способом и с применением какой-либо ГИС полезно для осмысления школьником хода решения и его результатов.
Рассмотрим еще один пример.
Пример 1
Постройте график функции  , и определите, при каких значениях параметра
, и определите, при каких значениях параметра 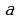 он имеет ровно две общие точки с прямой
он имеет ровно две общие точки с прямой  . (Слайд №12)
. (Слайд №12)
Вновь действуем по алгоритму.
Шаг первый (преобразование формулы, задающей функцию, и нахождение области ее определения).
Сначала преобразуем каждое уравнение отдельно.

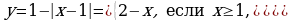 .
.
Тогда функция примет вид:  . Область определения
. Область определения  (все числа). Точками
(все числа). Точками 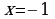 и
и  она разбивается на три промежутка, в которых функция задается разными формулами (Слайд №13).
она разбивается на три промежутка, в которых функция задается разными формулами (Слайд №13).
Шаги второй и третий (определение вида и характерных точек графика на каждом промежутке области определения; изображение графика функции на координатной плоскости).
На промежутке 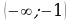 функция задана формулой
функция задана формулой  (квадратичная). График (парабола) может быть получен из графика функции
(квадратичная). График (парабола) может быть получен из графика функции  путем сдвига на 2 единицы влево, т.е. параллельным переносом на вектор
путем сдвига на 2 единицы влево, т.е. параллельным переносом на вектор 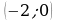 . Учащиеся строят этот фрагмент графика в тетради. Затем тот же фрагмент графика искомой функции строят в программе GeoGebra (Слайд №14).
. Учащиеся строят этот фрагмент графика в тетради. Затем тот же фрагмент графика искомой функции строят в программе GeoGebra (Слайд №14).

Далее на промежутке 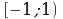 строят график линейной функции
строят график линейной функции 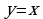 (фрагмент биссектрисы 1 и 3 координатных углов). Продолжают построение и в GeoGebra (Слайд №15).
(фрагмент биссектрисы 1 и 3 координатных углов). Продолжают построение и в GeoGebra (Слайд №15).
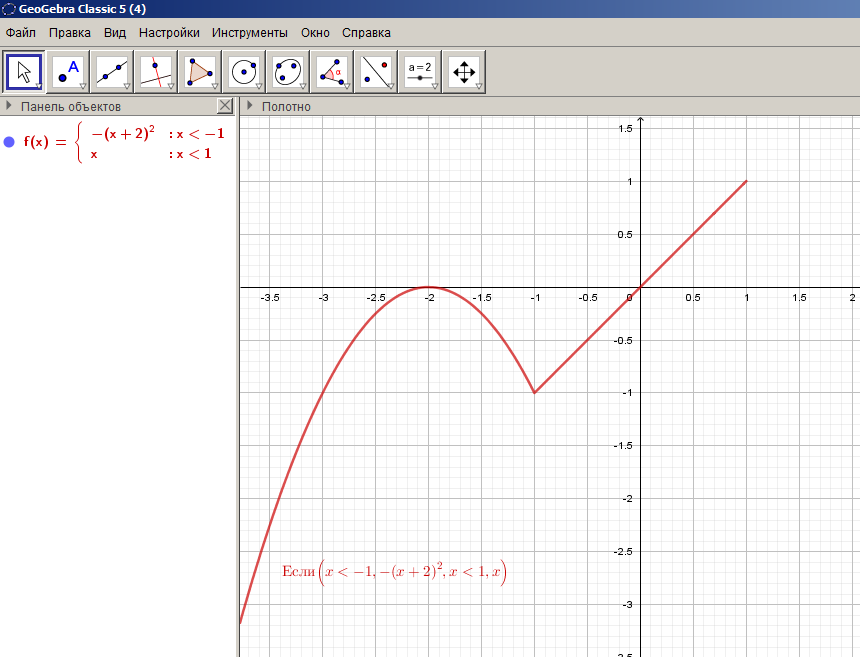
Завершаем построение графика еще одного фрагмента линейной функции 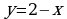 на промежутке
на промежутке  в тетради и ГИС (Слайд №16).
в тетради и ГИС (Слайд №16).
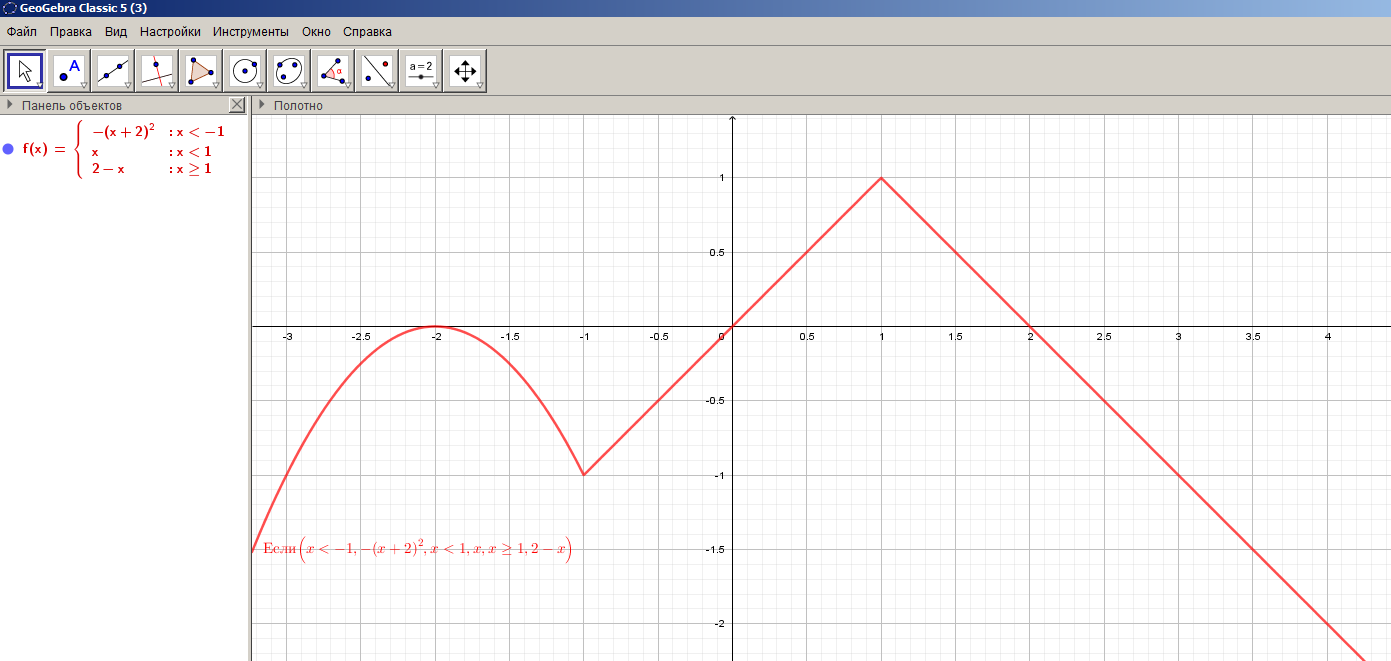
Шаг 4 (исследование графика функции в соответствии с вопросом к заданию).
Логичнее начать исследование в программе GeoGebra, так как после этого обучающимся становится понятно требование, содержащееся в вопросе (Слайд №17).
Детальнее процесс исследования с помощью GeoGebra представлен на следующих слайдах.
Если значение параметра 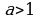 , то график функции и прямая
, то график функции и прямая  не имеют общих точек (Слайд №18) .
не имеют общих точек (Слайд №18) .

При достижении параметра значения, равного единицы ( ) график функции и прямая
) график функции и прямая  имеют одну общую точку (слайд 19).
имеют одну общую точку (слайд 19).
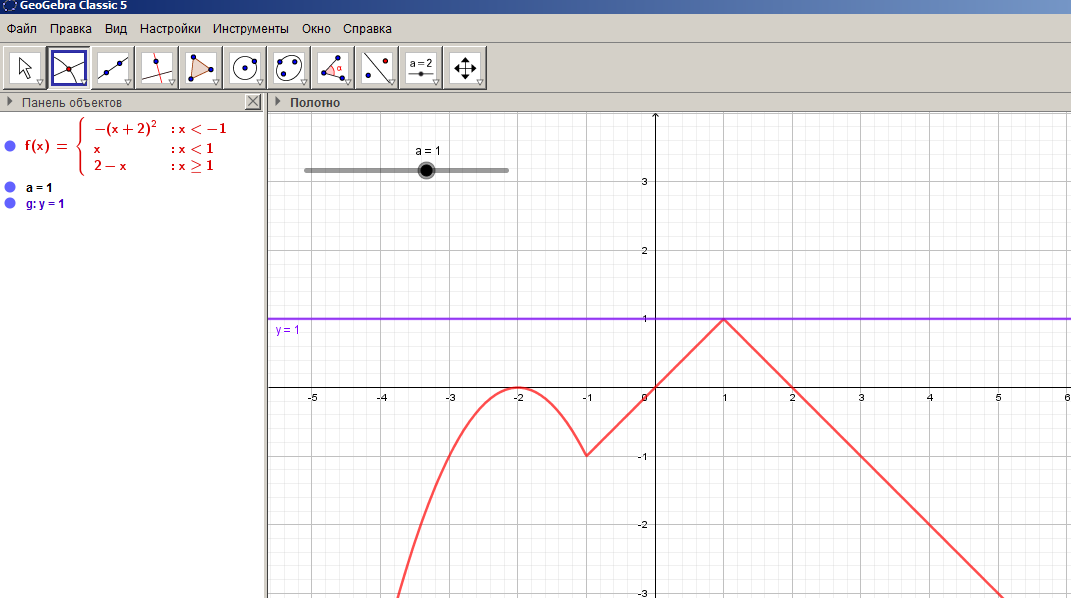
При  график функции и прямая
график функции и прямая  имеют две общих точки (слайд 20).
имеют две общих точки (слайд 20).
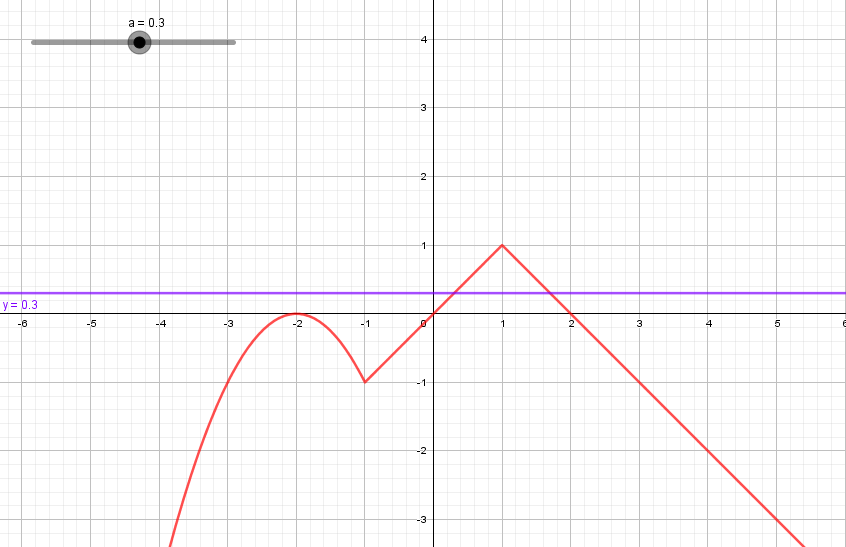
При 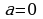 график функции и прямая
график функции и прямая  имеют три общих точки (слайд 21).
имеют три общих точки (слайд 21).

При 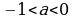 график функции и прямая
график функции и прямая  имеют четыре общих точки (слайд 22).
имеют четыре общих точки (слайд 22).
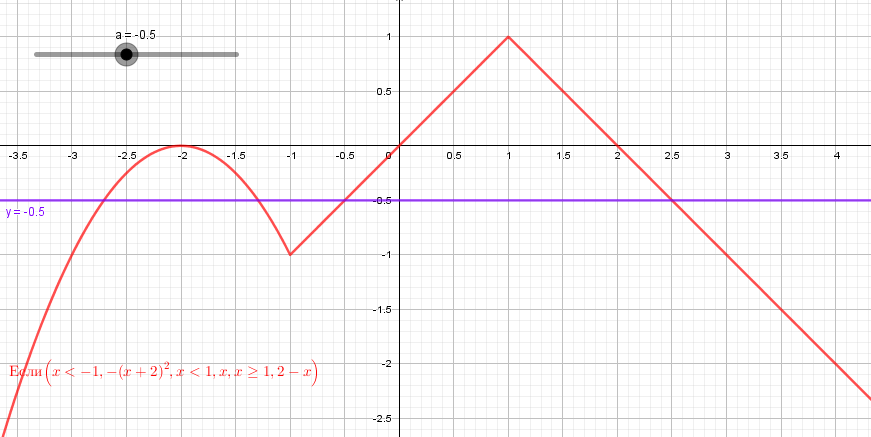
При 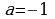 график функции и прямая
график функции и прямая  вновь имеют три общих точки (слайд 23).
вновь имеют три общих точки (слайд 23).

И, наконец, при  график функции и прямая
график функции и прямая  вновь имеют две общих точки (слайд 24).
вновь имеют две общих точки (слайд 24).

После исследования графика функции в соответствии с вопросом к заданию с помощью ГИС, переходим к решению вопроса задания по ими построенному в тетради графику.
Шаг пятый (запись ответа). Ответ:  ;
;  .
.
Решения подобных заданий с помощью GeoGebra более аккуратны, точны, иногда помогают сформулировать гипотезу для определения способа решения. Накапливая, таким образом, опыт решения задач с параметром с помощью построения графиков уравнений и неравенств, обучающиеся по виду задания представляют графики использованных в заданиях уравнений (неравенств), понимают суть вопроса к заданию (слайд 25) .





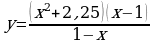 и определите, при каких значениях k прямая
и определите, при каких значениях k прямая  имеет с графиком ровно одну общую точку.
имеет с графиком ровно одну общую точку.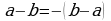 .
. . Таким образом, область определения функции
. Таким образом, область определения функции 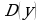 – все числа, кроме 1.
– все числа, кроме 1.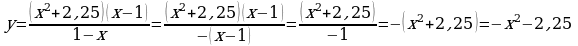
 в виде пунктирной прямой, подразумевая тем самым, что все ее точки не принадлежат графику исследуемой функции.
в виде пунктирной прямой, подразумевая тем самым, что все ее точки не принадлежат графику исследуемой функции.
 . По ее виду определяем, что графиком функции является парабола, ветви которой направлены вниз (
. По ее виду определяем, что графиком функции является парабола, ветви которой направлены вниз (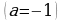 , вершина находится в точке
, вершина находится в точке 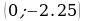 , т.к.
, т.к.  . Этой параболе не принадлежит точка
. Этой параболе не принадлежит точка 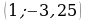 , так как
, так как 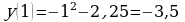 . График функции
. График функции  путем параллельного переноса на
путем параллельного переноса на  единичных отрезков вниз (или на вектор
единичных отрезков вниз (или на вектор  ).
). 
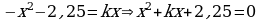 .
. 
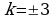 .
. , точка касания
, точка касания 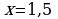 , а если
, а если 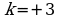 , точка касания
, точка касания 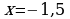 .
. 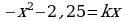 . Получим
. Получим 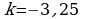 . При этом дискриминант этого уравнения будет больше нуля, значит, еще одно решение точно есть (Слайд №6).
. При этом дискриминант этого уравнения будет больше нуля, значит, еще одно решение точно есть (Слайд №6).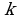 создадим ползунок, с помощью которого будем менять значения параметра, и наблюдать взаимное расположение прямой и параболы (Слайд №7).
создадим ползунок, с помощью которого будем менять значения параметра, и наблюдать взаимное расположение прямой и параболы (Слайд №7).



 .
. , и определите, при каких значениях параметра
, и определите, при каких значениях параметра 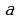 он имеет ровно две общие точки с прямой
он имеет ровно две общие точки с прямой  . (Слайд №12)
. (Слайд №12)
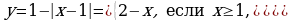 .
.  . Область определения
. Область определения  (все числа). Точками
(все числа). Точками 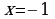 и
и 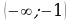 функция задана формулой
функция задана формулой  (квадратичная). График (парабола) может быть получен из графика функции
(квадратичная). График (парабола) может быть получен из графика функции 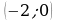 . Учащиеся строят этот фрагмент графика в тетради. Затем тот же фрагмент графика искомой функции строят в программе GeoGebra (Слайд №14).
. Учащиеся строят этот фрагмент графика в тетради. Затем тот же фрагмент графика искомой функции строят в программе GeoGebra (Слайд №14).
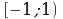 строят график линейной функции
строят график линейной функции 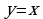 (фрагмент биссектрисы 1 и 3 координатных углов). Продолжают построение и в GeoGebra (Слайд №15).
(фрагмент биссектрисы 1 и 3 координатных углов). Продолжают построение и в GeoGebra (Слайд №15).
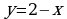 на промежутке
на промежутке  в тетради и ГИС (Слайд №16).
в тетради и ГИС (Слайд №16).
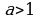 , то график функции и прямая
, то график функции и прямая 
 ) график функции и прямая
) график функции и прямая 
 график функции и прямая
график функции и прямая 
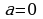 график функции и прямая
график функции и прямая 
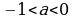 график функции и прямая
график функции и прямая 
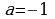 график функции и прямая
график функции и прямая 
 график функции и прямая
график функции и прямая 




















