Методическое пособие для подготовки к олимпиадам по физике. Задачи олимпиады Физтех 9 класс

1 . Камень брошен с поверхности Земли под углом к горизонту со скоростью V₀  10м/с. В верхней точке траектории скорость камня оказалась V  6 м/с. Сопротивление воздуха не учитывать. Принять ускорение свободного падения g  10м/с² . 1) Найти вертикальную составляющую скорости камня при броске. 2) Найти время полета камня до верхней точки траектории.

2. Бруски с массами m, 2m , 3m и 4m , соединенные легкими пружинами и нитью (см. рис.), удерживаются неподвижно с помощью упора на гладкой наклонной поверхности с углом наклона к горизонту  (sin  1/ 6 ). 1) Найти силу натяжения нити. 2) Найти ускорение (направление и модуль) бруска с массой 2m сразу после пережигания нити.

3 . Небольшой по размерам шарик массой m движется по окружности в горизонтальной плоскости, находясь от вертикальной оси вращения на расстоянии R. Шарик удерживается двумя нитями, угол между которыми 90⁰ (см. рис.). Верхняя нить составляет с осью вращения угол  (cos  4/ 5 ). Сила натяжения верхней нити в 3 раза больше, чем нижней. 1) Найти силу натяжения верхней нити. 2) Найти угловую скорость вращения.

4 . Тонкая трубка запаяна с одного конца, заполнена жидкостью плотностью  и закреплена на горизонтальной платформе (см. рис.). Открытое колено трубки вертикально и заполнено жидкостью до высоты H . Платформа вращается с угловой скоростью  вокруг вертикальной оси. Вертикальное колено находится на расстоянии R , а конец горизонтального - на расстоянии 7R от оси вращения. Атмосферное давление P₀ 1) Найти давление жидкости в месте изгиба трубки. 2) Найти давление жидкости в горизонтальном колене на расстоянии 2R от оси вращения.

5 . Клин массой 2m находится на шероховатой горизонтальной поверхности стола (см. рис.). Через блок, укреплённый на вершине клина, перекинута лёгкая нерастяжимая нить, связывающая грузы, массы которых m₁  3m и m ₂2 m . Грузы удерживают, затем отпускают. После этого грузы движутся, а клин покоится. Гладкая наклонная поверхность клина образует с горизонтом угол  (sin  0, 6 ). 1) Найдите ускорение грузов. 2) Найдите силу трения, действующую на клин со стороны стола.

4. Маленький шарик, брошенный под углом α к горизонту с начальной скоростью V₀  20 м/с, упруго ударяется о вертикальную стену, находящуюся на расстоянии L= 15 м от места броска. После удара шарик падает на горизонтальную поверхность земли на расстоянии l ₀  5м от стены. Плоскость стены перпендикулярна плоскости траектории шарика. 1) Найдите модуль скорости шарика при ударе о землю. 2) Найдите угол α, под которым был брошен шарик. Ускорение свободного падения принять равным g  10 м/с² . Известно, что при любых углах α справедливо sin2 2sin  cos .

1. Фейерверк массой m = 2 кг стартует после мгновенной работы двигателя с горизонтальной поверхности, летит вертикально вверх и разрывается в высшей точке траектории на множество осколков, которые летят во всевозможных направлениях с одинаковыми по величине скоростями. Высота точки разрыва H = 65 м. На землю осколки падают в течение  =10 с. 1) Найдите начальную скорость V₀ фейерверка. 2) Найдите суммарную кинетическую энергию K осколков сразу после взрыва. Ускорение свободного падения g=10 м/с² . Сопротивление воздуха считайте пренебрежимо малым.

2. На гладкой горизонтальной поверхности расположен клин. Гладкая наклонная поверхность клина образует с горизонтом угол  = 30⁰ . Шайбе, находящейся на наклонной поверхности клина, сообщают начальную скорость V₀ = 2 м/с (см. рис.), далее шайба безотрывно скользит по клину. Массы шайбы и клина одинаковы. Ускорение свободного падения g=10 м/с² . 1) На какую максимальную высоту H над точкой старта поднимется шайба на клине? 2) Найдите скорость V клина, в тот момент, когда шайба вернется в точку старта на клине. Массы шайбы и клина одинаковы. Ускорение свободного падения g=10 м/с² .

3. По внутренней поверхности проволочной металлической сферы радиуса R =1,2 м равномерно со скоростью V₀ = 3,7 м/с движется модель автомобиля. Движение происходит в горизонтальной плоскости большого круга. Масса модели m = 0,4 кг. Модель приводится в движение двигателем. Силу сопротивления считайте пренебрежимо малой. 1) С какой по величине силой P модель действует на сферу? 2) Рассмотрим модель автомобиля равномерно движущуюся по окружности в плоскости большого круга, составляющей с горизонтом угол  = . Вычислите минимальную допустимую скорость V_MIN такого равномерного движения. Коэффициент трения скольжения шин по поверхности сферы  = 0,9. Ускорение свободного падения g=10 м/с² .

1 . Камень брошен с некоторой скоростью V₀ под углом = 45⁰ к горизонту (см. рис.). Максимальная высота полета камня H =10 м. В конце полета камень падает на горизонтальную крышу, высота которой над точкой старта h = 7 м. 1) Найдите начальную скорость V₀ камня. 2) Найдите cos (см. рис.), здесь  - угол, который вектор скорости образует с горизонтом в момент завершения полета. Ускорение свободного падения g =10 м/с² . Силу сопротивления воздуха считайте пренебрежимо малой.

3. На гладкой горизонтальной поверхности вплотную к вертикальной стенке стоит брусок, в бруске сделано гладкое углубление в форме полусферы радиуса R (см. рис.). Из точки А с нулевой начальной скоростью скользит шайба массы m . Через некоторое время шайба достигает максимальной высоты H = , отсчитанной от нижней точки полусферы. 1) Найдите массу M бруска. 2) Найдите максимальную скорость V_MAX бруска при дальнейшем движении системы. 3) С какой по величине силой P брусок действует на горизонтальную поверхность в тот момент, когда его скорость V_MAX ? Ускорение свободного падения g .

1 . Мальчик бросает вертикально вверх мяч. В момент, когда мяч достиг максимальной высоты, мальчик бросает вертикально вверх второй мяч, с того же места и с той же скоростью, что и первый. В результате мячи столкнулись на высоте H от места броска. Сопротивление воздуха не учитывать. 1. Найти время полёта второго мяча до столкновения. 2. Найти начальную скорость мячей. 3. Какой путь прошёл первый мяч до столкновения?

2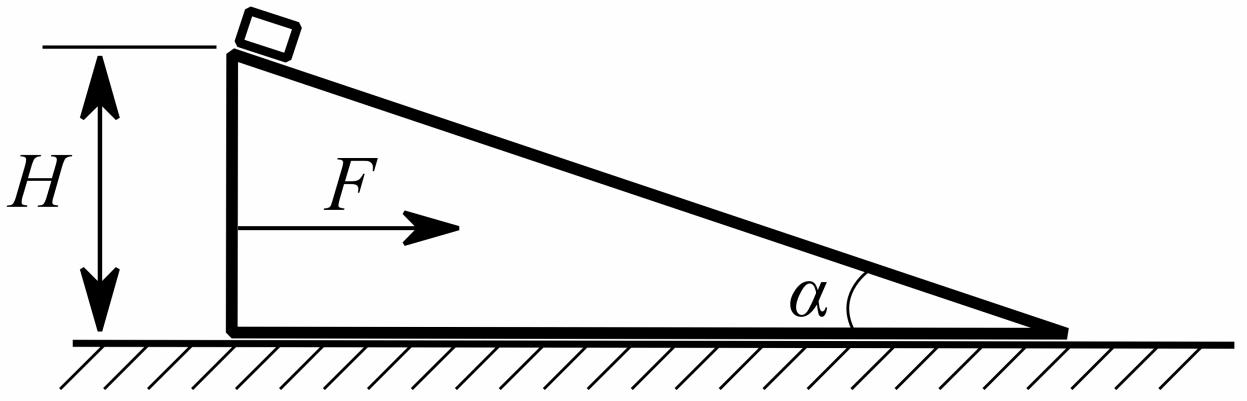 . Конический сосуд с водой и шаром, лежащим на дне сосуда, вращается вокруг вертикальной оси OO₁ с угловой скоростью ω (см. рис.). Плотность воды ρ, плотность шара 3ρ. Радиус шара R, центр шара находится на расстоянии 2R от оси вращения. Угол между горизонтальным дном и боковой стенкой сосуда α (tg α = 2). Внутренняя поверхность сосуда гладкая. 1. С какой силой N₁ шар давил бы на дно, если бы сосуд не вращался? 2. Найти силу N₂ давления шара на дно при вращении сосуда.

4. На гладкой горизонтальной поверхности стола находится клин. Гладкая поверхность клина составляет угол α (cos α = 4/5) с горизонтом (см. рис.). На вершине клина на высоте H удерживают небольшую по размерам шайбу массой m. Масса клина 3m. 1. За какое время шайба съедет с клина, если клин удерживать, а шайбу отпустить? На покоившийся вначале клин стали действовать с постоянной горизонтальной силой F = 2mg, а шайбу отпустили. В результате клин стал двигаться поступательно по столу, а шайба вниз по клину. 2. Найти ускорение клина. 3. Через какое время шайба достигнет стола? Направления всех движений в одной вертикальной плоскости

1. Дальность полёта камня, брошенного под углом α = 60^◦ к горизонту, равна S = 17 м. 1. Найдите начальную скорость V₀ камня. Через некоторое время по траектории камня летит модель самолёта массой m = 1 кг с постоянной по величине скоростью V = V₀/4. 2. В высшей точке траектории найдите вертикальную составляющую силы F, с которой воздух действует на модель самолёта. Ускорение свободного падения g = 10 м/с² . Силу сопротивления воздуха в процессе полёта камня считайте пренебрежимо малой. Точки старта и окончания полёта лежат в одной горизонтальной плоскости

2 . Маленькая коробка съезжает по наклонной плоскости, образующей угол α = 30^◦ с горизонтом. Коэффициент трения скольжения коробки по поверхности на высотах меньших h = 2 м равен µ₁ = 0,81, на больших высотах коэффициент трения скольжения равен µ₂ = 0,11. Начальная скорость коробки нулевая. У основания наклонной плоскости коробка останавливается. 1. Найдите продолжительность T движения коробки на участке торможения. 2. С какой высоты H съехала коробка? Ускорение свободного падения g = 10 м/с² .

3. Однородный шар радиуса R = 5 см подвешен на нерастяжимой нити длиной l = 15 см к гладкой вертикальной стенке сосуда (см. рис.). Масса шара m = 0,8 кг. 1. С какой по величине N силой шар действует на стенку сосуда? Сосуд заполняют водой и приводят во вращение вокруг вертикальной оси, проходящей через точку крепления нити к стенке. Угловая скорость вращения ω = 10 рад/с, шар находится полностью в воде вдали от стенок. 2. Какой угол α нить образует с вертикалью? Ускорение свободного падения g = 10 м/с² .

1 . Камень бросают с вышки со скоростью V₀ = 8 м/с под углом α = 60^◦ к горизонту. В полете камень все время приближался к горизонтальной поверхности Земли и упал на нее со скоростью 2,5V₀. 1. Найти вертикальную компоненту скорости камня при падении на Землю. 2. Найти время полета камня. 3. Найти горизонтальное смещение камня за время полета. Ускорение свободного падения принять g = 10 м/с² . Сопротивление воздуха не учитывать.

2 . Человеку, упирающемуся в ящик ногами, надо передвинуть ящик из состояния покоя по горизонтальному полу на расстояние S к стене (см. рис.). Массы человека и ящика равны соответственно m и M = 5m. Натянутые части каната, не соприкасающиеся с блоком, горизонтальны. Массами каната, блока и трением в оси блока можно пренебречь. Коэффициент трения между ящиком и полом µ. 1. С какой силой ящик с человеком давят на пол при движении ящика? 2. С какой минимальной постоянной силой F₀ надо тянуть человеку канат, чтобы осуществить задуманное? 3. Какой скорости достигнет ящик, если человек осуществит задуманное, приложив постоянную силу F (F F₀) к канату?

3. Однородный шар массой m и радиусом R находится на гладкой поверхности клина, наклоненной под углом α к горизонту (см. рис.). Шар удерживается нитью длиной L, привязанной к вертикальной оси, проходящей через вершину клина. Нить параллельна поверхности клина. 1. Найти силу натяжения нити, если система покоится. 2. Найти силу натяжения нити, если система вращается с угловой скоростью ω вокруг вертикальной оси, проходящей через вершину клина, а шар не отрывается от клина.

4 . Трубка, изогнутая под прямым углом, расположена в вертикальной плоскости и заполнена маслом (см. рис.). Угол α = 45^◦ . При равноускоренном движении трубки в горизонтальном направлении уровни масла в коленах трубки устанавливаются на высотах h₁ = 8 см и h₂ = 12 см. 1. Найдите ускорение a трубки. 2. С какой максимальной скоростью V будет двигаться жидкость относительно трубки после того как трубка внезапно станет двигаться равномерно (ускорение «исчезнет»)? Ускорение свободного падения g = 10 м/с². Действие сил трения пренебрежимо мало

2. На противоположных концах тележки массы M, находящейся на гладкой горизонтальной поверхности, стоят два ученика одинаковой массы m каждый. Длина тележки L. Вначале система неподвижна. Один ученик бросает мяч, а другой ловит. Масса мяча m₁. В процессе полета горизонтальная составляющая скорости мяча относительно поверхности, на которой находится тележка, равна V₀. 1. Найдите скорость V₁ тележки после броска. 2. Найдите продолжительность T полета мяча. 3. Найдите скорость V₂ тележки после того, как второй ученик поймает мяч. Силу сопротивления воздуха считайте пренебрежимо малой

4 . Тонкая Γ-образная трубка с горизонтальным коленом, закрытым с одного конца, и вертикальным коленом высотой H = 40 мм, открытым в атмосферу, заполнена полностью ртутью (см. рис.). Если трубку двигать (в плоскости рисунка) с ускорением, не большим некоторого a₀, то ртуть из трубки не выливается. 1. Найти давление P₁ внутри трубки в точке A, находящейся от вертикального колена на расстоянии 1/3 длины горизонтального колена, если трубка движется с ускорением a₀. 2. Найти давление P₂ в точке A, если трубка движется с ускорением 0,6a₀. 3. Найти давление P₃ вблизи закрытого конца трубки, если она движется с ускорением 0,8a₀. Атмосферное давление P₀ = 740 мм рт. ст. Давлением насыщенных паров ртути в условиях опыта пренебречь. Ответы дать в «мм рт. ст.».

1. Пушка установлена на плоском склоне горы, образующем угол α = 30◦ с горизонтом. При выстреле «вверх» по склону снаряд падает на склон на расстоянии S₁ = 700 м от места выстрела. В момент падения скорость снаряда перпендикулярна поверхности склона. Пушку разворачивают на 180◦ и производят второй выстрел «вниз» по склону. Затем пушку перемещают на горизонтальную поверхность и производят третий выстрел. Ускорение свободного падения g = 10 м/с² . Силу сопротивления воздуха считайте пренебрежимо малой. Угол наклона ствола к поверхности, с которой стреляют, при всех выстрелах одинаков. 1. На каком расстоянии S₂ от места второго выстрела снаряд упадет на склон? 2. Найдите дальность L стрельбы при третьем выстреле.

2. На шероховатой горизонтальной поверхности стола покоится чаша. Внутренняя поверхность чаши — гладкая полусфера радиуса R. На дне чаши лежит небольшая шайба массы m. Масса чаши 3m. Ударом шайбе сообщают горизонтальную скорость V₀ = , здесь g — ускорение свободного падения. Скольжение чаши начинается в тот момент времени, когда вектор скорости шайбы повернется на угол α = . 1. С какой силой P шайба действует на чашу в этот момент? 2. Вычислите коэффициент µ трения скольжения чаши по столу

3. Гладкая упругая шайба радиуса R, движущаяся со скоростью V₀, упруго сталкивается с такой же шайбой, покоящейся на гладкой горизонтальной поверхности. В результате столкновения скорость налетающей шайбы уменьшается вдвое. 1. Найдите расстояние d от центра покоившейся шайбы до прямой, по которой двигался центр налетающей шайбы. 2. Через какое время T после соударения расстояние между центрами шайб будет равно S?

1. Теннисист тренируется на горизонтальной площадке, посылая мяч к вертикальной стенке. В первом случае мяч летит практически с уровня земли с начальной скоростью V₀ = 22 м/с под углом α = 30◦ к горизонту и ударяется в стенку. Во втором случае мяч стартует из той же точки со скоростью под углом 2α к горизонту и ударяется в ту же точку стенки. Соударения мяча со стенкой абсолютно упругие. Мяч движется в вертикальной плоскости перпендикулярной стенке. Силой сопротивления воздуха пренебречь. Ускорение свободного падения g = 10 м/с² . 1. На какой максимальной высоте H находился мяч в полете в первом случае? 2. На какой высоте h мяч ударяется в стенку? 3. Через какое время τ после удара о стенку мяч упадет на площадку во втором случае?

2 . Тонкостенный полый шар радиуса R = 0,1 м зажат между двумя горизонтальными параллельными пластинами, одна из которых движется вправо со скоростью V₁ = 0,6 м/с, а вторая — влево со скоростью V₂ = 0,4 м/с. Проскальзывания между пластинами и шаром нет. На внутренней поверхности полого шара сидит жук массы m = 1 г. Ускорение свободного падения g = 10 м/с² . 1. Найдите скорость V центра шара. 2. Найдите максимальную силу P_max, с которой жук действует на шар.

3. Две одинаковые гладкие упругие шайбы движутся по гладкой горизонтальной поверхности. Скорость первой шайбы V , скорость второй ( −2V) . Для каждой шайбы прямая, сонаправленная с вектором скорости и проходящая через центр шайбы, касается другой шайбы. Происходит абсолютно упругое соударение. 1. Найдите скорость V₁ (по модулю) первой шайбы после соударения. 2. На какой угол α повернется вектор скорости первой шайбы в результате соударения?

1 . Систему из бруска массой m₁ = m и доски массой m₂ = 2m, находящихся на горизонтальном столе, приводят в движение, прикладывая к доске горизонтальную силу F (см. рис.). Коэффициент трения между столом и доской и между горизонтальной поверхностью доски и бруском равен µ. Массой горизонтально натянутой нити, массой блока и трением в его оси пренебречь. 1) Найти ускорение a₁ доски, если бы не было трения. 2) Найти ускорение a₂ доски, если есть трение и параметры F, m, µ подобраны так, что есть движение.

2. Пустую стеклянную бутылку опускают в цилиндрический сосуд с водой с вертикальными стенками. Бутылка стала плавать, а уровень воды в сосуде поднялся на H₁ = 3 см. Затем в бутылку медленно наливают воду. Когда масса налитой воды достигает некоторой величины, бутылка начинает тонуть. Уровень воды в сосуде за время наливания поднялся ещё на H₂ = 1 см. Плотность стекла ρ₀ = 3 г/см³ , плотность воды ρ = 1 г/см³ . Площадь внутреннего сечения сосуда S = 250 см² . 1) Найти массу пустой бутылки. 2) Найти массу воды, налитой в бутылку. 3) Найти вместимость пустой бутылки.

3. Ракета стартует вертикально. К t₁ = 30 секунде полёта вес выводимого на орбиту спутника увеличился в k₁ = 1,5 раза (относительно веса перед стартом), к t₂ = 60 секунде полёта вес спутника был уже в k₂ = 2,0 раза больше, чем перед стартом. Считать массовый расход топлива постоянным. Сопротивлением воздуха и изменением ускорения свободного падения с высотой пренебречь. Принять g = 10 м/с² . 1) Найти ускорение ракеты в момент времени t₁. 2) Определите скорость u вытекания продуктов сгорания относительно сопла, считая её постоянной.

1. Шарик, скользящий по гладкой горизонтальной поверхности, догоняет брусок, который движется в том же направлении по этой поверхности. Грань бруска, о которую ударяется шарик, перпендикулярна вектору скорости шарика. Масса бруска много больше массы шарика. После упругого столкновения шарик скользит в первоначальном направлении с кинетической энергией, которая в 4 раза меньше его начальной кинетической энергии. Найти отношение начальных скоростей скольжения шарика и бруска.