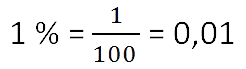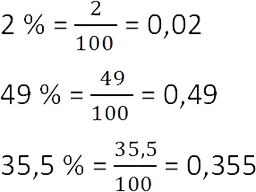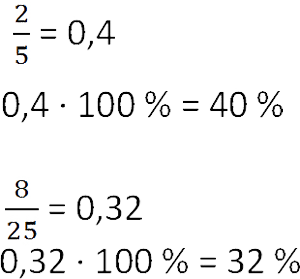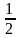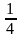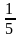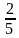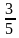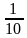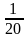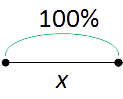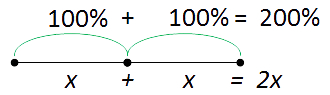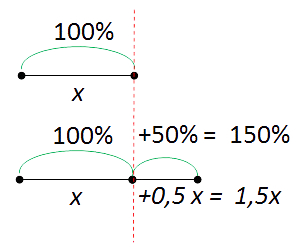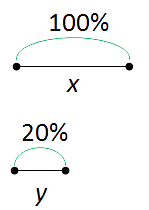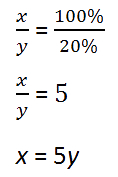ОТДЕЛ ОБРАЗОВАНИЯ МАРТУКСКОГО РАЙОНА
РАЙОННЫЙ МЕТОДИЧЕСКИЙ КАБИНЕТ
Методическое пособие
по математике по теме: «Проценты»

Составитель: учитель математики
Дәніш Ә.Е.
Мартук, 2021 год
Рассмотрено на заседании районного методического совета
«___» ___________20___г
Заведующий методическим кабинетом отдела образования Мартукского района: __________________ Балмагамбетова С.Х.
Составитель: учитель математики Казанской общеобразовательной основной школы Дәніш Әсем Еділқызы
Рецензент: Антипова Райля Абдулловна – методист отдела образования Мартукского района
В данном пособии собраны материалы по решению задач на нахождения процента от числа, числа по его проценту, а также практических задач на применение свойств процента.
Пояснительная записка.
«Числа управляют миром», – говорили пифагорейцы.
Но числа дают возможность человеку управлять миром,
и в этом нас убеждает весь ход развития науки и техники наших дней.
(А. Дородницын)
Современные дети растут в условиях интенсивно формирующейся рыночной экономики страны. Для них необходимыми стали знания таких областей наук, как экономика, маркетинг, управление, потому что профессии, которые они получат на основе этих знаний, будут не только престижны, но и высокооплачиваемые.
Тема «Проценты» изучается в курсе математики 5, 6 классов. Для усвоения данной темы школьникам необходимо иметь достаточный уровень развития абстрактного мышления, но в возрасте 10-11 лет абстрактное мышление еще недостаточно развито, поэтому учащиеся 5, 6 классов усваивают проценты с трудом. В последующих классах в действующих учебниках алгебры проценты встречаются крайне редко, и каждый раз вызывают большие затруднения у школьников. Это особенно становится заметным при организации повторения в процессе подготовки к итоговой аттестации за курс девятого класса: даже стандартные задачи, взятые из «Экзаменационного сборника» вызывают затруднения у большинства учащихся.
Велика также роль процентов в повседневной жизни, очень часто приходится решать задачу типа «Товар стоит а рублей, потом его цену снизили на р %, затем еще на b %. Сколько стал стоить товар? Решение даже этой простейшей задачи на проценты у многих вызывает затруднение.
В программу старших классов по математике тема «Проценты» не входит, навыки работы с процентами забываются. В основном с задачами на проценты учащиеся сталкиваются на уроках химии и решают их с помощью пропорций, поэтому учащиеся не видят универсальность процентов и не могут решать простейшие задачи на проценты, встречающиеся в другой сфере деятельности человека.
Требование вузов к математической подготовке с каждым годом возрастают. Экзамен по математике в любой вуз всегда содержит задачи на проценты. Уровень требований, предъявляемый к абитуриентам по данной теме, высок. На вступительных экзаменах по математике предлагаются задачи на «сплавы», «смеси», «концентрации», задачи экономического содержания, которые решаются с помощью сложных процентов, а школьная программа не содержит задач такого типа.
Введение.
Слово процент от латинского слова pro centum, что буквально означает «за сотню» или «со ста». Идея выражения частей целого постоянно в одних и тех же долях, вызванная практическими соображениями, родилась еще в древности у вавилонян. Ряд задач клинописных табличек посвящен исчислению процентов, однако вавилонские ростовщики считали не «со ста», а «с шестидесяти».
Проценты были особенно распространены в Древнем Риме. Римляне называли процентами деньги, которые платил должник заимодавцу за каждую сотню. От римлян проценты перешли к другим народам Европы. Долгое время под процентами понимались исключительно прибыль или убыток на каждые сто рублей. Они применялись только в торговых и денежных сделках. Затем область их применения расширилась, проценты встречаются в хозяйственных и финансовых расчетах, статистике, науке и технике.
Ныне процент — это частный вид десятичных дробей, сотая доля целого (принимаемого за единицу). Знак % происходит, как полагают, от итальянского слова cento (сто), которое в процентных расчетах часто писалось сокращенно cto. Отсюда путем дальнейшего упрощения в скорописи буква t превратилась в наклонную черту (/), возник современный символ для обозначения процента. В школьном учебнике "Математика, 5 «авторов Н.Я. Виленкина и др. дана еще одна любопытная версия возникновения знака %. Там, в частности, говорится, что этот знак произошел в результате нелепой опечатки, совершенной наборщиком. В 1685 г. в Париже была опубликована книга-руководство по коммерческой арифметике, где по ошибке наборщик вместо cto напечатал %.
Современная жизнь делает задачи на проценты актуальными, так как сфера практического приложения процентных расчетов расширяется. Вопросы инфляции, повышение цен, рост стоимости акций, снижение покупательской способности касаются каждого человека в нашем обществе. Планирование семейного бюджета, выгодного вложения денег в банки, невозможны без умения производить несложные процентные вычисления.
Сами проценты не дают экономического развития, но их знание помогает в развитии практических способностей, а также умение решать экономические задачи. Обдуманное изучение процентов может способствовать развитию таких навыков как экономичность, расчетливость.
В вариантах вступительных экзаменов встречаются задачи на проценты, и эти задачи часто вызывают затруднения у школьников. Причина в том, что тема «Проценты» изучается в младших 5-6 классах.
Решение задач на проценты и процентное содержание, концентрацию, смеси и сплавы с преимущественным использованием основных правил действия с десятичными и обыкновенными дробями.
Цель работы: Составить практическое пособие по решению задач на проценты для школьников.
Задачи:
-
Изучить исторический и теоретический материал по интересующему вопросу.
-
Систематизировать задачи на проценты по типам.
-
Составить практические рекомендации по решению задач на проценты.
-
Выявить практическое применение таких задач.
-
Определить план дальнейшей работы над темой.
Практическая значимость работы. Данное пособие по решению задач на проценты будет интересно не только школьникам 5-6 класса, которым интересна математика. Здесь найдут много полезного и выпускники школ, и абитуриенты при подготовке к выпускным и вступительным экзаменам.
Основные типы задач по теме «Проценты».
В данной главе приводятся примеры задач, которые решаются с применением определения, что такое один процент, как выразить дробь в процентах и правилам нахождения части (дроби) от числа, и числа по значению его части (дроби), т.е. это те темы и задачи, которые рассматриваются в школе.
Обращаем внимание, что существуют и другие способы решения простейших задач на проценты, например, составляют пропорции на каждом шаге, но в этом случае решение становится на несколько шагов длиннее. Мы же видим свою задачу в нахождении более быстрых способов решения таких задач, в связи с тем, что в настоящее время редкий тест по математике для абитуриентов, обходится без задач, в которых не упоминались бы проценты.
1.1. Решение задач на применение основных понятий о процентах.
Сотая часть метра — это сантиметр, сотая часть рубля — копейка, сотая часть центнера — килограмм. Люди давно замети, что сотые доли величин удобны в тактической деятельности. Потому для них было придумано специальное название — процент. Значит одна копейка — один процент от одного рубля, а один сантиметр — один процент от одного метра.
Один процент — это одна сотая доля числа. Математическими знаками один процент записывается так: 1%.
Определение одного процента можно записать равенством: 1 % = 0,01 * а
5%=0,05, 23%=0,23, 130%=1,3 и т. Д
Как найти 1% от числа? Раз 1% это одна сотая часть, надо число разделить на 100. Деление на 100 можно заменить умножением на 0,01. Поэтому, чтобы найти 1% от данного числа, нужно умножить его на 0,01. А если нужно найти 5% от числа, то умножаем данное число на 0,05 и т.д.
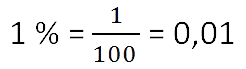
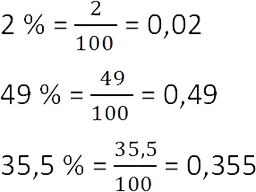
Чтобы перевести десятичную дробь в проценты, нужно дробь умножить на 100 и добавить знак «%».
0,14 = 0,14 · 100% = 14%
0,07 = 0,07 · 100% = 7%
0,565 = 0,565 · 100% = 56,5%
Чтобы перевести обыкновенную дробь в проценты, нужно сначала превратить её в десятичную дробь.
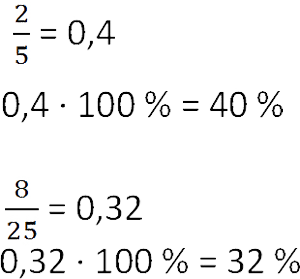
Как вы поняли, проценты тесно связаны с обыкновенными и десятичными дробями. Поэтому стоит запомнить несколько простых равенств.
В повседневной жизни нужно знать о числовой связи дробей и процентов. Так, половина — 50%, четверть — 25%, три четверти — 75%, одна пятая — 20%, а три пятых — 60%.
Знание наизусть соотношений из таблицы внизу облегчит вам решение многих задач.
1 = 100%
| Картинка | Обыкновенная дробь | Десятичная дробь | Процент |
| 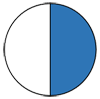
| 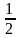
| 0,5 | 50% |
| 
| 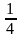
| 0,25 | 25% |
| 
|
| 0,75 | 75% |
| 
| 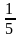
| 0,2 | 20% |
| 
| 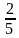
| 0,4 | 40% |
| 
| 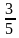
| 0,6 | 60% |
| 
| 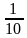
| 0,1 | 10% |
| 
| 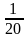
| 0,05 | 5% |
Пример. Найти: 35% от 120.
Решение:
1) 35% = 0,35;
2) 120 * 0,35 = 42.
Ответ: 42.
Правило 1. Чтобы найти данное число процентов от числа, нужно проценты записать десятичной дробью, а затем число умножить на эту десятичную дробь
Пример. Токарь вытачивал за час 40 деталей. Применив резец из более прочной стали, он стал вытачивать на 10 деталей в час больше. На сколько процентов повысилась производительность труда токаря?
Решение:
Чтобы решить эту задачу, надо узнать, сколько, процентов составляют 10 деталей от 40. Для этого найдем сначала, какую часть составляет число 10 от числа 40. Мы знаем, что нужно разделить 10 на 40. Получится 0,25. А теперь запишем в процентах — 25%.
Получаем ответ: производительность труда токаря повысилась на 25%.
Правило 2. Чтобы найти, сколько процентов одно число составляет от другого, нужно разделить первое число на второе и полученную дробь записать в виде процентов.
Пример. При плановом задании 60 автомобилей в день завод выпустил 66 автомобилей. На сколько процентов завод выполнил план?
Решение: Какую часть составляют изготовленные автомобили от количества автомобилей по плану. Запишем в процентах =110%
Ответ: 110%
Сложение и вычитание процентов
Проценты складываются и вычитаются друг с другом как обычные числа.
Примеры:
1% + 37% − 25% = 38% − 25% = 13%
70% − (42% + 3%) = 70% − 45% = 25%
В повседневной жизни полезно знать разные формы выражения одного и того же изменения величин, сформулированных без процентов и с помощью процентов.
Например, увеличить в 2 раза, значит увеличить на 100%. Разберёмся, почему это так. Пусть «x» — это 100%.
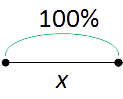
Тогда, увеличив «x» в 2 раза, получим «2x».
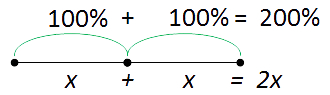
Сравним полученные результаты.

Получилось, что общее количество процентов равно 200%. Увеличить в 2 раза означает увеличить на 100% и наоборот.
Рассуждая, таким же образом, докажем, что увеличить на 50%, значит увеличить в 1,5 раза .
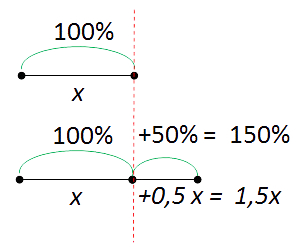
Уменьшение числа также может быть выражено в процентах.
Пусть «x» — 100%. Известно, что «x» уменьшилось на 80%. Найдём, во сколько раз уменьшилось «x». Вначале найдём, сколько процентов от x осталось.
100% − 80% = 20%
20% осталось от «x». Обозначим остаток «x» за «y».
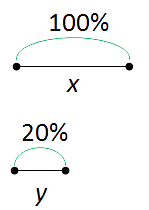
Составим пропорцию. По числовому коэффициенту определяем, во сколько раз уменьшился «x».
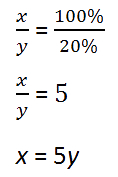
Таким образом, мы установили, что уменьшить на 80%, значит уменьшить в 5 раз.
Поняв связь между процентами и «разами», вы без труда сможете понимать, о чём так часто говорят в новостях и в газетах, приводя различные статические данные.
Значение фраз «увеличить и уменьшить на … процентов»
Увеличить на 50%, значит увеличить в 1,5 раза.
на 100% → в 2 раза
на 150% → в 2,5 раза
на 200% → в 3 раза
на 300% → в 4 раза
Уменьшить на 80%, значит уменьшить в 5 раз.
на 75% → в 4 раза
на 50% → в 2 раза
на 25% → в ≈ 1,33 раза
на 20% → в 1,25 раза
Пример.
1. На сколько процентов 10 больше 6?
2. На сколько процентов 6 меньше 10?
Решение:
1. ((10 — 6)*100%)/6 = 66 2/3 %
2. ((10 — 6)*100%)/10 = 40%
Ответ: 66 2/3 %, 40 %.
Пример. Бронза является сплавом олова и меди. Сколько процентов сплава составляет медь в куске бронзы, состоящем из 6 кг олова и 34 кг меди?
Решение: 1) 6+ 34 =40 (кг) масса всего сплава.
2) = 85% сплава составляет медь.
Ответ. 85%.
Пример. Что произойдет с ценой товара, если сначала ее повысить на 25%, а потом понизить на 25%?
Решение: Пусть цена товара х руб, тогда после повышения товар стоит 125% прежней цены, т.е. 1,25х;, а после понижения на 25% , его стоимость составляет 75% или 0, 75 от повышенной цены, т.е. 0,75 *1,25х= 0,9375х, тогда цена товара понизилась на 6, 25 %, т.к. х — 0,9375х = 0,0625х ; 0,0625х/х . 100% = 6,25%
Ответ: первоначальная цена товара снизилась на 6,25%.
Правило 3. Чтобы найти процентное отношение двух чисел А и В, надо отношение этих чисел умножить на 100%, то есть вычислить (а/в)*100%.
Пример. Найти число, если 15% его равны 30.
Решение:
1) 15% = 0,15;
2) 30 : 0,15 = 200.
Или через уравнение:
х — данное число; 0,15.х = 300;
х = 200.
Ответ: 200.
Пример. Из хлопка-сырца получается 24% волокна. Сколько надо взять хлопка-сырца, чтобы получить 480кг волокна?
Решение. Запишем 24% десятичной дробью 0,24 и получим задачу о нахождении числа по известной ему части (дроби). 480 : 0,24= 2000 кг = 2 т
Ответ: 2 т
Пример. Сколько кг белых грибов надо собрать для получения 1 кг сушеных, если при обработке свежих грибов остается 50% их массы, а при сушке остается 10% массы обработанных грибов?
Решение. 1кг сушеных грибов — это 10% или 0,01 часть обработанных, т.е.
1 кг : 0,1=10 кг обработанных грибов, что составляет 50% или 0,5 собранных грибов, т.е. 10 кг : 0,05=20 кг
Ответ: 20 кг
Пример. Свежие грибы содержали по массе 90% воды, а сухие 12%. Сколько получится сухих грибов из 22 кг свежих?
Решение:
1) 22 . 0,1 = 2,2 (кг) — грибов по массе в свежих грибах; (0,1 это 10% сухого вещества)
2) 2,2 : 0,88 = 2,5 (кг) — сухих грибов, получаемых из свежих (количество сухого вещества не изменилось, но изменилось его процентное содержание в грибах и теперь 2,2 кг это 88% или 0,88 сухих грибов).
Ответ: 2,5 кг.
Правило 4. Чтобы найти число по данным его процентам, надо выразить проценты в виде дроби, а затем значение процентов разделить на эту дробь.
1.2. Решение задач на понятия «процентное содержание», «концентрация», «%-й раствор».
Процентное содержание. Процентный раствор.
Пример. Сколько кг соли в 10 кг соленой воды, если процентное содержание соли 15%.
Решение. 10 . 0,15 = 1,5 (кг) соли.
Ответ: 1,5 кг.
Процентное содержание вещества в растворе (например, 15%), иногда называют %-м раствором, например, 15%-й раствор соли.
Пример. Сплав содержит 10 кг олова и 15 кг цинка. Каково процентное содержание олова и цинка в сплаве?
Решение: Процентное содержание вещества в сплаве — это часть, которую составляет вес данного вещества от веса всего сплава.
-
10 + 15 = 25 (кг) — сплав;
-
10/25 . 100% = 40% — процентное содержание олова в сплаве;
-
15/25 . 100% = 60% — процентное содержание цинка в сплаве;
Ответ: 40%, 60%.
Концентрация.
Если концентрация вещества в соединении по массе составляет р%, то это означает, что масса этого вещества составляет р% от массы всего соединения.
Пример. Концентрация серебра в сплаве 300 г составляет 87%. Это означает, что чистого серебра в сплаве 261 г.
Решение. 300 . 0,87 = 261 (г).
В этом примере концентрация вещества выражена в процентах.
Отношения объема чистой компоненты в растворе ко всему объему смеси называется объемной концентрацией этой компоненты.
Сумма концентраций всех компонент, составляющих смесь, равна 1.
Если известно процентное содержание вещества, то его концентрация находится по формуле: К=р/100% к — концентрация вещества; р — процентное содержание вещества (в процентах).
Пример. Имеется 2 сплава, в одном из которых, содержится 40%, а в другом 20% серебра. Сколько кг второго сплава нужно добавить к 20 кг первого, чтобы после сплавления вместе получить сплав, содержащий 32% серебра?
Решение: Пусть к 20 кг первого сплава нужно добавить х кг второго сплава. Тогда получим (20 + х) кг нового сплава. В 20 кг первого сплава содержится 0,4 . 20 = 8 (кг) серебра, в х кг второго сплава содержится 0,2х кг серебра, а в (20+х) кг нового сплава содержится 0,32 . (20+х) кг серебра. Составим уравнение:
8 + 0,2х = 0,32 . (20 +х); х = 13 1/3.
Ответ: 13 1/3 кг второго сплава нужно добавить к 20 кг первого, чтобы получить сплав, содержащий 32% серебра.
Пример. К 15 л 10%-ного раствора соли добавили 5%-ный раствор соли и получили 8%-ный раствор. Какое количество литров 5%-ного раствора добавили?
Решение. Пусть добавили х л 5%-ного раствора соли. Тогда нового раствора стало (15 + х) л, в котором содержаться 0,8 . (15 + х) л соли. В 15 л 10%-ного раствора содержится 15 * 0,1 = 1,5 (л) соли, в х л 5%-ного раствора содержится 0,05х (л) соли.
Составим уравнение.
1,5 + 0,05х = 0,08 . (15 + х);
х = 10.
Ответ: добавили 10 л 5%-ного раствора
1.3. Решение задач с использованием понятия коэффициента увеличения.
Чтобы увеличить положительное число а на р процентов, следует умножить число а на коэффициент увеличения к=(1+0,01р).
Чтобы уменьшить положительное число а на р процентов, следует умножить число а на коэффициент уменьшения к= (1-0,01р).
Пример. Вклад, вложенный в сбербанк два года назад, достиг суммы, равной 13125 руб. Каков был первоначальный вклад при 25% годовых?
Решение. Если а (рублей) — размер первоначального вклада, то в конце первого года вклад составит 1,25а а в конце второго года размер вклада составит 1,25 *1,25а. Решая уравнение 1,25* 1,25а=13125, находим а=8400.
Ответ: 8400 руб.
Пример. В феврале цена на нефть увеличилась на 12% по сравнению с январской. В марте цена нефти упала на 25%. На сколько процентов мартовская цена изменилась по сравнению с январской?
Решение. Если х — январская цена нефти, то февральская цена нефти равна
(1 +0,01*12)х = 1,12х. Чтобы вычислить мартовскую цену у на нефть, следует умножить февральскую цену 1,12х на (1-0,01*25)=0,75, т.е. у=0,75 1,12х=0,84х , мартовская цена отличается от январской на (0,84х)/х100 —100=84-100= −16(%), т.е. цена упала на 16 %
Ответ: цена упала на 16%.
Правило 5. Чтобы найти, на сколько % положительное число у отличается от положительного числа а, следует вычислить, сколько % у составляет от а, а затем от полученного числа отнять а.
Глава 2. Разные задачи на проценты (с решениями).
В данной главе рассматривается выборка задач из различных источников, которые охватывают весь теоретический материал, который излагался выше, предлагаем свои решения. Отметим, что предложенный способ решения не является единственным.
2.1 Тестовые задания на проценты.
Задача 1.Товар стоил тысячу рублей. Продавец поднял цену на 10%, а через месяц снизил её на 10%.Сколько стал стоить товар?
Решение. Пусть товар стоил 1000руб., после повышения цены на 10% он стал стоить 1,1*1000 руб. После понижения этой цены на 10%, он стал стоить 0,9*1,1*1000=990 руб.
Ответ. 990 руб.
Задача 2.Собрали 100 кг грибов. Оказалось, что их влажность 99%. Когда грибы подсушили, влажность снизилась до 98%. Какой стала масса этих грибов после подсушивания?
Решение. Так как влажность грибов составляет 99%, это означает, что на так называемое «сухое вещество приходится 1% грибов, т.е 1 кг, после сушки влажность составляет 98%, т.е. на «сухое вещество» приходится 2%, т.е 1кг это 0,02 подсушенных грибов, 1 кг : 0,02=50 кг.
Ответ. 50 кг.
Задача 3. Цена входного билета на стадион была 1 рубль 80 копеек. После снижения входной платы число зрителей увеличилось на 50% , а выручка выросла на 25% .Сколько стал стоить билет после снижения?
Решение. Пусть зрителей, до понижения цены, на стадион приходило А чел. и выручка составляла 1,8А руб. После понижения цены, цена 1,8*р, зрителей стало 1,5А, выручка составляет 1,8*р*1,5*А руб. С другой стороны, выручка повысилась на 25%, т.е. составляет 1,25*1,8А. Получаем 1,8*р*1,5*А=1,25*1,8А., откуда р=12,5/15, тогда билет стоит 1,8*12,5/15=1,5 руб.
Ответ. 1руб. 50 коп
Задача 4. По дороге идут два туриста. Первый из них делает шаги на 10% короче и в то же время на 10% чаще, чем второй. Кто из туристов идет быстрее и почему?
Решение. Пусть второй турист делает а шагов, каждый из которых равен в, тогда ав это длина пройденного пути. А первый турист тогда прошел1,1*а*0,9*в=0,99*ав, что меньше ав.
Ответ. Второй турист идет быстрее.
Задача 5. Цену за товар уменьшили на 10%, а затем еще на 10%. Стоит ли он дешевле, если цену сразу снизить на 20%?
Решение. Если товар стоил А руб, после двух понижений он стал стоить 0,9*0,9*А=0,81А. А цену товара сразу понизить на 20%, то он станет стоить 0,8*А , что дешевле.
Ответ. Да.
Задача 6. Числитель дроби увеличили на 20%. На сколько процентов надо уменьшить её знаменатель, чтобы в итоге дробь возросла вдвое?
Решение. Пусть данная дробь, новая дробь, откуда К=0,6, что означает, что знаменатель нужно уменьшить на 40%
Ответ. 40%
Задача 7. Матроскин продает молоко через магазин и хочет получать за него 25 рублей за литр. Магазин удерживает 20% стоимости проданного товара. По какой цене будет продаваться молоко в магазине?
Решение. Пусть молоко продает магазин по А руб, тогда после удержания 20% стоимости товара, Матроскину остается 0,8*А=25, откуда А=31, 25 руб.
Ответ. 31 руб. 25 коп.
Задача 8. Один покупатель купил 25% имевшегося куска полотна, второй покупатель 30% остатка, а третий — 40% нового остатка. Сколько (в процентах) полотна осталось непроданным?
Решение. Пусть полотна было р . Первый купил 0,25р,, осталось (1-0,25)р полотна, второй покупатель купил 0,3*0,75р=0,225р, осталось 0,75р —0,225р=0,525р, третий купил 0,4*0,525р=0,21р, осталось 0,525р-0,21р=0,315р, что составляет 31,5% от р.
Ответ. 31,5%
Задача 9. Бригада косарей в первый день скосила половину луга и еще 2 га, а во второй день 25% оставшейся части и последние 6 га. Найти площадь луга.
Решение. 6 га составляют 75% или 0,75=3/4 от оставшейся части после 1 дня работы, т.е.6: 0,75=6 га 8+2=10 га — это половина луга, весь луг 20 га
Ответ. 20 га
Задача 10. Как изменится в процентах площадь прямоугольника, если его длина увеличится на 30%, а ширина уменьшится на 30%?
Решение. АВ- площадь исходного прямоугольника, 1,3*А*0,7*В=0,91АВ — площадь нового прямоугольника, что составляет 91% исходного.
Ответ. Уменьшится на 9%
Задача 11. В драматическом кружке число мальчиков составляет 80% от числа девочек. Сколько процентов составляет число девочек в этом кружке от числа мальчиков?
Решение. Девочек А чел, мальчиков 0,8*А, девочки составляют от мальчиков А/(0,8А)= 1,25, т.е. 125 % от числа мальчиков
Ответ. 125%
Задача 12. В бассейн проведена труба. Вследствие засорения её приток воды уменьшился на 60%. На сколько процентов вследствие этого увеличится время, необходимое для заполнения бассейна
Решение. Пусть Х — объем воды, который должен поступить за время Т при притоке А в ед времени., т.е. Х=АТ. Так как приток уменьшился на 60%, т.е. стал составлять 0,4А, тогда время стало ТК. Получим АТ=0,4А*КТ, откуда К = 2,5, что составляет 250% от времени, необходимого на заполнение бассейна до засорения, т.е. время увеличилось на 150%
Ответ. 150%
Задача 13. 5 литров сливок с содержанием жира 35% смешали с 4 литрами 20%-ных сливок и к смеси добавили 1 литр чистой воды. Какой жирности получилась смесь?
Решение. 0,35*5+0,2*4=р*(5+4+1), откуда р=0,255, что составляет 25,5%
Ответ. 25,5%
2.2. Избранные задачи на нахождение процентов.
Задача №1. Предприятие изготовило за квартал 500 насосов, из которых 60% имели высшую категорию качества. Сколько насосов высшей категории качества изготовило предприятие?
Решение:
Найдем 60% от 500 (общее количество насосов).
60 % = 0,6
500 · 0,6 = 300 насосов высшей категории качества.
Ответ: 300 насосов высшей категории качества.
Задача №2. Банк предлагает вклад «студенческий». По этому вкладу, сумма, имеющаяся на 1 января, ежегодно увеличивается на одно и то же число процентов. Вкладчик положил 1 января 1000 руб. и в течение 2 лет не производил со своим вкладом никаких операций. В результате вложенная им сумма увеличилась до 1210 руб. На сколько процентов ежегодно увеличивалась сумма денег, положенная на этот вклад?
Решение. Используя формулу увеличения положительного число на p%, получим, что через год сумма вклада составит 1000*(1+0,01р), а через два года 1000*(1+0,01р)2=1210, т.е. (1+0,01р)2=1,21, 1+0,01р=1,1, 0,01р=0,1, откуда р=10%
Ответ: сумма ежегодно увеличивалась на 10%.
Задача №3. Владелец дискотеки имел стабильный доход. В погоне за увеличением прибыли он повысил цену на билеты на 25%. Количество посетителей резко уменьшилось, и он стал нести убытки. Тогда он вернулся к первоначальной цене билетов. На сколько процентов, владелец дискотеки снизил новую цену билетов, чтобы она стала равна первоначальной?
Решение. Пусть цена билета была А руб. После повышения на 25% цена стала 1,25А, после понижения цена билета стала р*1,25А. Т.к. цена билета вернулась к первоначальной, то получим р*1,25А=А, откуда р=1/1,25 = 0,8, что означает, что новая цена составляет 80% цены после повышения., значит владелец дискотеки снизил цену на 20%.
Ответ: 20%
Задача №4. Ученик прочитал 138 страниц, что составляет 23% числа всех страниц в книге. Сколько страниц в книге?
Решение:
Итак, нам неизвестно сколько всего страниц в книге. Но мы знаем, что часть, которую прочитал ученик (138 страниц) составляет 23% от общего количества страниц в книге.
Так как 138 стр. — это всего лишь часть, само количество страниц, естественно, будет больше 138. Это поможет нам при проверке.
Проверка: 600 138 (это означает, что 138 является частью 600).
Ответ: 600 (стр.) — общее количество страниц в книге.
Задача №5. Из 200 арбузов 16 оказались незрелыми. Сколько процентов всех арбузов составили незрелый арбузы?
Решение:
О чем спрашивают? О незрелых арбузах. Значит, 16 делим на общее количество арбузов и умножаем на 100%.
Ответ: 8% — составляют незрелые арбузы от всех арбузов.
Задача №6. Предприятие уменьшило выпуск продукции на 20%. На сколько процентов, необходимо теперь увеличить выпуск продукции, чтобы достигнуть его первоначального уровня?
Решение. Пусть А количество продукции, выпускаемое предприятием, 0,8А-количество продукции, которое стало выпускать предприятия после уменьшения на 20%. Из условия задачи следует уравнение р*0,8А=А, где р —коэффициент увеличения, откуда р=1/0,8=1,25, что означает, что необходимо увеличить выпуск продукции на 25%.
Ответ: 25%
Задача №7. К 120 г раствора, содержащего 80% соли, добавили 480 г раствора, содержащего 20 % той же соли. Сколько процентов соли содержится в получившемся растворе?
Решение. 1) 0,8*120=96(г)-соли в первоначальном растворе;
2) 480*0,2=96(г) соли во втором растворе;
3) ((96+96)/(120+480))*100%=32%-процентное содержание соли в получившемся растворе.
Ответ: 32%
Задача №8. За год стипендия студента увеличилась на 32%. В первом полугодии стипендия увеличилась на 10%. Определить, на сколько процентов увеличилась стипендия во втором полугодии?
Решение. Пусть А- первоначальный размер стипендии, 1,1А — размер стипендии после повышения в 1 полугодии, р*1,1А- размер стипендии после увеличения во 2 полугодии, где р- коэффициент увеличения. Так как за год стипендия увеличилась на 32%, получим уравнение р*1,1А=1,32А, р=132/110=1,2, что означает , что стипендия во 2 полугодии составляет 120% стипендии 1 полугодия., т.е. стипендия во 2 полугодии увеличилась на 20%
Ответ: на 20%.
Задача №9. Имеются два слитка сплава золота с медью. Первый слиток содержит 230 г золота и 20 г меди, а второй слиток — 240 г золота и 60 г меди. От каждого слитка взяли по куску, сплавили их и получили 300 г сплава, в котором оказалось 84 % золота. Определить массу ( в граммах) куска, взятого от первого слитка.
Решение. Определим процентное содержание золота в обоих слитках. 1) 230+20=250(г)-масса 1 слитка, 230/250=0,92 (92%)процентное содержание золота в 1 слитке.
2) 240+60=300(г) —масса 2 слитка, 240/300=0,8 (80%)- процентное содержание золота во 2 слитке. Пусть х масса куска, взятого от 1 слитка, (300-х)- масса куска, взятого от 2 слитка, получим уравнение 0,92х+0,8(300-х)=0,84*300, откуда х=100
Ответ: 100г.
Задача №10. Первый сплав серебра и меди содержит 70 г меди, а второй сплав — 210 г серебра и 90 г меди. Взяли 225 г первого сплава и кусок второго сплава, сплавили их и получили 300 г сплава, который содержит 82 % серебра. Сколько граммов серебра содержалось в первом сплаве?
Решение. Пусть х г серебра содержится в 1 сплаве., тогда 70/(х+70)-какую часть 1 сплава составляет медь, 90/(210+90)-такую часть составляет медь во 2 сплаве., кусок второго сплава 300-225=75г, тогда получаем уравнение.
225*(70/(х+70))+75*(90/300)=(1-0,82)*300, откуда х=430г
Ответ: 430г
Задача №11. В колбе было 200 г 80% -го спирта. Провизор отлил из колбы некоторое количество этого спирта и затем добавил в нее столько же воды, чтобы получить 60% — ый спирт. Сколько граммов воды добавил провизор?.
Решение. 200*0,8=160(г)-масса чистого спирта в колбе, их колбы отлили х г раствора, осталось (200-х)г раствора, в котором чистого спирта 0,8*(200-х). Когда к раствору добавили х г воды, то масса раствора снова стала 200 г, а концентрация
[(0,8*(200-х))/200]*100%=60%, откуда х=50(г).
Ответ: провизор добавил 50г воды.
Задача №12. В колбе было 800 г 80% -ного спирта. Провизор отлил из колбы 200 г этого спирта и добавил в нее 200 г воды. Определить концентрацию ( в процентах) полученного спирта.
Решение. После того, как провизор отлил 200 г раствора, стало 600г, в котором чистого спирта 0,8*600=480г, когда добавили200г воды, то раствор снова 800г, а концентрация чистого спирта в растворе (480/800)*100%=60%
Ответ: 60%
Задача №13. Численность населения в городе Таганроге в течение двух лет возрастала на 2 процента ежегодно. В результате число жителей возросло на 11312 человек. Сколько жителей было в Таганроге первоначально?
Решение. А- первоначальное количество жителей Таганрога. Используя формулу коэффициента увеличения, получаем
А(1+0,02)2=А+11312, откуда А=280000
Ответ: 280000 чел
Задача №14. Из сосуда, доверху наполненного 94% -м раствором кислоты, отлили 1,5 л жидкости и долили 1,5 л 70% -го раствора этой же кислоты. После этого в сосуде получился 86% раствор кислоты. Сколько л раствора вмещает сосуд?
Решение. Пусть х л вмещает сосуд, тогда из условий задачи следует уравнение 0,94(х-1,5)+0,7*1,5=0,86х, откуда х=4,5 л.
Ответ: 4,5 л
Задача №15. Денежный вклад в банк за год увеличивается на 11 %. Вкладчик внес в банк 7000 рублей. В конце первого года он решил увеличить сумму вклада и продлить срок действия договора еще на год, чтобы в конце второго года иметь на счету не менее 10000 рублей. Какую наименьшую сумму необходимо дополнительно положить на счет по окончании первого года, чтобы при той же процентной ставке (11 %) реализовать этот план? (Ответ округлите до целых.)
Решение. 1,11* 7000=7770руб-будет на счете в конце 1 года. Пусть х руб. положили дополнительно на счет, из условия задачи получаем неравенство 1,11(7770+х) 10000, получим х1239, 1/111, что означает, чтобы на счету было не менее 10000 руб, нужно положить не менее12 40руб.
Ответ: 1240 руб.
Задача №16. Организм взрослого человека на 70% состоит из воды. Какова масса воды в теле человека, который весит 76 кг?
Решение
1) 76 : 100 = 0,76 (кг) 1% от массы человека;
2) 0,76 * 70 = 53,2(кг).
Ответ: масса воды 53,2 кг.
Задача №17. Металлический конструктор состоит из 300 деталей. 12% этих деталей гайки. Сколько гаек в металлическом конструкторе?
Решение
1) 300 : 100 = 3(детали) 1% всех деталей конструктора;
2) 3 * 12 = 36 (гаек).
Ответ: в конструкторе 36 гаек.
Задача №18. В грушах сладких сортов содержится сахара 15% от их массы. Сколько кг сахара будет содержаться в 6 кг груш?
Решение
1) 6 : 100 = 0,06 (кг) 1% от шести килограмм;
2) 0,06 * 15 = 0,9 (кг).
Ответ: в шести кг груш будет содержаться 0,9 кг сахара.
Задача №19. В классе 30 человек, из них девочек – 18. Сколько процентов мальчиков в классе?
Решение
1) 30 : 100 = 0,3 - 1% процент всех детей класса;
2) 30 – 18 = 12 – мальчиков в классе;
3) 12 : 0,3 = 40%.
Ответ: в классе учится 40% мальчиков.
Задача №20. Если высушить свежие груши, то их масса уменьшится на 80%. Сколько понадобится свежих груш для приготовления 8 кг сушеных?
Решение
1) 100 – 80 = 20% - составляет масса сухих груш относительно свежих;
2) 8 : 20 = 0,4 (кг) 1% свежих груш для приготовления 8 кг сушеных;
3) 0,4 * 100 = 40 (кг).
Ответ: понадобится 40 кг свежих груш.
Задача №21. 1% процент книги, которую читал Сережа, составляет 4 страницы. Сколько страниц осталось прочитать Сереже, если он уже прочитал 30%?
Решение
1) 30 * 4 = 120 (стр.) прочитал Сережа;
2) 4 * 100 = 400 (стр.) все страницы книги;
3) 400 – 120 = 280 (стр.).
Ответ: Сереже осталось прочесть 280 страниц.
Задача №22. Количество сливок, получаемых из молока, равно 21%. Сколько сливок получиться, если использовать 48 литров молока?
Решение
1) 48 : 100 = 0,48 (л) 1% от 48 литров;
2) 0,48 * 21 = 10,08 (л).
Ответ: сливок получится 10,08 литров.
Задача №23. Периметр прямоугольника равен 80 см. 60% этого периметра – сумма длин прямоугольника. Чему равна ширина прямоугольника?
Решение
1) 80 : 100 = 0,8 (см) 1% от периметра прямоугольника;
2) 100 – 60 = 40% - часть суммы ширин в периметре;
3) 0,8 * 40 = 32 (см);
4) 32 : 2 = 16 (см).
Ответ: ширина прямоугольника равна 16 см.
Задача №25. Одна из сторон треугольника равна 15 см, длина второй равна 80% первой, а длина третей – 150% второй. Чему равен периметр этого треугольника?
Решение
1) 12 : 100 = 0,15 (см) 1% от длины первой стороны;
2) 0,15 * 80 = 12 (см) длина второй стороны;
3) 12 : 100 = 0,12 (см) 1% от длины второй стороны;
4) 0,12 * 150 = 18 см (см) длина третьей стороны.
5) 12 + 15 + 18 = 45 (см).
Ответ: периметр треугольника равен 45 см.
Задача №26. На приготовление ужина у мамы ушло 2 часа. Для приготовления мясных блюд понадобилось 40% времени, десерт занял 20%, все остальное время было затрачено на приготовление салатов. Сколько времени понадобилось маме для приготовления каждого из блюд?
Решение
1) 40 + 20 = 60% времени ушло у мамы на приготовление мясных блюд и десерта;
2) 100 – 60 = 40% времени заняло приготовление салатов;
2 часа = 120 мин.
3) 120 : 100 = 1,2 (мин) 1% от 2 часов;
4) 40 * 1,2 = 48 (мин);
5) 20 * 1,2 = 24 (мин).
Ответ: на приготовление салатов 48 мин, на приготовление мясных блюд 48 минут, на приготовление десерта 24 минуты.
Задача №27. В течении месяца Саша играл с папой в шахматы. За это время было сыграно 25 партий, из которых 80% выиграл папа. Сколько партий в шахматы выиграл за месяц Саша?
Решение
1) 100 – 80 = 20% партий выиграл Саша;
2) 25 : 100 = 0,25 – 1% процент от всех партий;
3) 20 * 0,25 = 5 (партий).
Ответ: Саша выиграл 5 партий.
Задача №28. У Лены в аквариуме 8 меченосцев, что составляет 40% всех ее рыбок. Сколько всего рыбок у Лены в аквариуме?
Решение
1) 8 : 40 = 0,2 - 1% от всех рыбок;
2) 0,2 * 100 = 20 (рыбок).
Ответ: всего у Лены 20 рыбок в аквариуме.
Задача №29. За зиму медведь Вини Пух съел 16 горшочков меда. Сколько горшочков меда заготовил Вини Пух, если у него осталось 20% всех его запасов?
Решение
1) 100 – 20 = 80% - меда съел за зиму Вини Пух;
2) 16 : 80 = 0,2 (меда) 1% от всего меда;
3) 0,2 * 100 = 20.
Ответ: на зиму Вини Пух заготовил 20 горшочков меда.
Задача №30. Грибы теряют при сушке 75% своей массы. Сколько понадобится свежих грибов для приготовления 4 кг сушеных?
Решение
1) 100 – 75 = 25% масса сушеных грибов от массы свежих;
2) 4 : 25 = 0,16 1% от массы свежих грибов;
3) 0,16 * 100 = 16 (кг).
Ответ : понадобится 16 кг свежих грибов.
Задача №31. На олимпиаде школьная команда набрала 72 очка. Сколько очков можно набрать на олимпиаде, если набранные командой очки составляют 80% из всех возможных?
Решение
1) 72 : 80 = 0,9(очков) 1% от всех возможных очков;
2) 0,9 * 100 = 90 (очков).
Ответ: на олимпиаде можно набрать 90 очков.
Задача №32. Вкладчик внес в банк 1200 р. В какую сумму вклад превратится через год, если банк начисляет доход в размере 4% годовых?
Решение:Найдем какое вознаграждение банк доложит вкладчику. Для этого умножим 1200 р. на процент годовых 4%.
-
4% = 0,04
-
1200 · 0, 04 = 48 р. — такое вознаграждение доложит банк вкладчику через год.
-
Теперь найдем общую сумму, которую заберет вкладчик через год.
1200 + 48 = 1248 р. — в такую сумму превратится вклад через год.
Ответ: 1248 р. — в такую сумму превратится вклад через год.
Задача №33. Цена изделия составляет 5000 р. На изделие предложена скидка 10%. Найти цену товара с учетом скидки.
Решение:
Найдем скидку в рублях.
-
10% = 0,1
-
5000 · 0,1 = 500 р. — скидка в рублях.
-
Теперь найдем цену товара с учетом скидки.
5000 − 500 = 4500 р. — цена товара с учетом скидки.
Ответ: 4500 р. — цена товара с учетом скидки.
Задача №34. Килограмм соли растворили в 9 л воды. Чему равна концентрация полученного раствора? (Масса 1 л воды составляет 1 кг)
Решение:
1 кг — масса растворённого вещества (соли)
9 кг — масса воды в растворе (не путать с общей массой раствора)
9 + 1 = 10 кг — общая масса раствора.
Ответ:
10% — концентрация раствора.
Задача №35. В растворе 40% соли. Если добавить 120 г соли, то процентное содержание соли станет равным 70. Сколько грамм соли было первоначально в растворе?
Решение: Для составления пропорции обозначим за «x» первоначальную массу соли в растворе, а за «y» массу воды в растворе. Так как концентрация соли в исходном растворе 40%, то соответственно вода составляет
100% − 40%= 60%
Изобразим графически условия задачи.
Составим пропорцию, связывающую эти величины до добавления соли.
Для решения задачи нам надо определить какая из неизвестных («x» или «y») остаётся неизменной после добавления соли.
Этой величиной является масса воды в растворе «y».
Выразим её, учитывая изменения в растворе после добавления соли.
(x + 120) г — масса соли в новом растворе
(100% − 70% = 30% — процентное содержание воды в новом растворе.
Составим пропорцию аналогично предыдущей, но с учётом изменений произошедших после добавления соли.
Так как масса воды осталось неизменной после добавления соли, приравняем её значения до и после добавления соли и решим уравнение.
Ответ: 48 г — масса соли в первоначальном растворе.
Задача №36 В нашей школе добросовестно учатся 540 учеников, а еще 60 человек валяют дурака. Сколько всего учеников в школе и какой процент из них валяют дурака?
Решение:
1). 540 + 60 = 600 (чел.) – учится в школе.
2). 60 : 600 = 0,10 =10% - валяют дурака.
Ответ: 600чел., 10%
Задача №37. 40 бабушек вошли в автобус. 70% бабушек купили билеты, а остальные закричали, что у них проездной. Контролер проверил. На самом деле оказалось, что проездной был у семи бабушек. Сколько бабушек ехали “зайцами”?
Решение:
1) 40 : 100 * 70 = 28 (б.) – купили билеты. (иначе 40 : 10 * 7 = 28)
2) 40-28=12 (б.) – с проездными.
3) 12 – 7 = 5 (б.)
Ответ: 5 бабушек ехали “зайцами”.
Задача №38. Доктор Айболит со своими друзьями плыл на корабле в страну Лимпопо, чтобы вылечить больных зверей. Когда они проплыли 60% пути, на них напали пираты во главе с Бармалеем и посадили корабль на мель. Но друзья обманули злых пиратов и оставшиеся
80 км пути проделали на пиратском корабле. Сколько километров преодолели друзья, чтобы попасть в страну Лимпопо?
1). 100 – 60 = 40 (%) пути осталось.
2). 80 : 40 * 100 = 200 (км.)
Ответ: 200 км преодолели друзья, чтобы попасть в страну Лимпопо.
Задача №39. Матроскин продает молоко через магазин и хочет иметь по 32 рубля за литр. Но, магазин удерживает 20% стоимости проданного товара. По какой цене нужно продавать молоко?
Решение. Прием цену 1 л молока, по которой Матроскин должен сдавать его в магазин за100%, тогда 26 рублей составляет 80%. Отсюда
32 : 8 * 10 = 40 рублей.
Ответ: молоко нужно продавать по 40 рублей.
Задача №40. В этом году среднестатистический житель города Мурманска платит за коммунальные услуги 7 000 рублей. Известно, что ежегодно коммунальные услуги дорожают примерно на 8%. Какова будет стоимость коммунальных услуг в начале 4-го года.
Решение:
1 год оплачивается по 7 000 рублей ежемесячно. 2 год с учетом увеличения на 8% оплачивается 7000*1,08=7560 рублей ежемесячно.
3 год с учетом увеличения прошлогодней оплаты на 8% оплачивается 7560*1,08=8164,8 рублей ежемесячно.
Начало 4-го года и весь 4-ый год 8164,8*1,08=8817,984 рублей
Это же решение выражением
7000 * 1,08 * 1,08 * 1,08 = 8817,984 рублей
Ответ: в начале 4-го года стоимость коммунальных услуг станет 8817,984 рублей.
Задача №41. Олег Владимирович собирается взять в банке кредит 1,2 миллион рублей под 11% годовых. Условия выплаты такие: каждый год ровно в день взятия кредита банк начисляет процент, после чего возможна выплата. За сколько лет Олег Владимирович выплатит этот кредит, если он готов выплачивать не более 390 тысяч рублей в год?
Решение. После взятия кредита долг банку будет составлять 1200000 р., через год банк начислит процент и долг до выплаты будет составлять 1200000 + 132000 = 1332000 р., а после выплаты
1332000 – 390000 = 942000 р. и т.д.
Запишем все выплаты и начисления в таблицу:
| Время | Долг банку | Остаток после выплаты |
| Первый год | 1200000 | выплаты не было |
| Конец первого года | 1332000 | 942000 |
| Конец второго года | 1045620 | 655620 |
| Конец третьего года | 727738,2 | 337738,2 |
| Конец четвёртого года | 374889,5 | 374889,5 |
Ответ: 4.
Задача №42. Среди 45000 жителей города 40% не интересуется футболом. Среди футбольных болельщиков 70% смотрело по телевизору финал Чемпионата мира. Сколько жителей города смотрело этот матч?
Решение:
45 000*0,6*0,7=18900 (чел.)
Ответ: 18900 жителей города смотрело этот матч.
Задача №43. Банк предложил вкладчику следующие варианты процентной ставки по вкладу. Два раза в год по 10% или 1 раз в год 20%. Равноценны ли эти предложения. Если нет, то какое предложение выгоднее.
Решение. Примем за х рублей сумму вклада и запишем выражением оба варианта.
-
вариант. 1,1 * 1,1 * х = 1,21 х рублей.
-
вариант. 1,20 х рублей.
Ответ: нет, выгоднее 1 вариант.
Задача №44. Имеется 2 раствора соли массой 80 г и 120 г. В первом растворе содержится 12 г соли, а во втором – 15 г соли. Какова концентрация каждого раствора? Какова будет концентрация,
если оба раствора смешать?
1) 12 : 80 = 0,15 = 15 (%) концентрация 1-го раствора.
2) 15 : 120 = 0,125 = 12,5 (%) концентрация 2-го раствора.
3) 27 : 200 = 0,135 = 13,5 (%) концентрация смеси.
Ответ: 15%, 12,5%, 13,5%
Задача №45. В банк на депозит на 3 года положили 30000 рублей под 10% годовых.
а) Найдите насколько прибыльнее был бы вариант, когда годовой доход добавлять к счету, на который в будут начисляться проценты, чем вариант, когда проценты каждый год забираются клиентом?
б) Какая будет разница через 10 лет?
Решение:
а) Для первого случая используем формулу для вычисления сложных процентов:
| 30000(1 + | 10% | )3 = 30000 · 1.13 = 39930 |
| 100% |
прибыль в этом случае равна
39930 - 30000 = 9930
Во втором случае годовой доход будет равен
соответственно прибыль за три года будет равна
3000 · 3 = 9000
Первый метод будет выгоднее второго на
9930 - 9000 = 930 рублей
б) Для первого случая используем формулу для вычисления сложных процентов:
| 30000(1 + | 10% | )10 = 30000 · 1.110 ≈ 77812.27 |
| 100% |
прибыль в этом случае равна
77812.27 - 30000 = 47812.27
Во втором случае годовой доход будет равен
соответственно прибыль за десять лет будет равен
3000 · 10 = 30000
Первый метод будет выгоднее второго на
47812.27 - 30000 = 17812.27 рублей
Ответ: а) 900 рублей;
б) 17812.27 рублей.
Раздаточный материал (карточки) по теме: Проценты
| КАРТОЧКА № 1.1 Запишите в виде десятичной дроби 3 %, 15 %, 123 %. Найдите 1%, 10 %, 50 % от числа 300. Сколько процентов суток составляют 12 часов? Найдите число, 25 % которого равны 50. |
| КАРТОЧКА № 1.2 Запишите в виде десятичной дроби 5% , 24 %, 136 %. Найдите 1 %, 10 %, 50 % от числа 200. Сколько процентов суток составляют 18 часов? Найдите число, 25 % которого равны 40. |
| КАРТОЧКА № 1.3 Запишите в виде десятичной дроби 7 %, 48 %, 135 %. Найдите 1%, 10%, 50% от числа 500. Сколько процентов суток составляют 6 часов? Найдите число, 25 % которого равны 60. |
| КАРТОЧКА № 2.1 В магазине баскетбольные мячи составляют 14% всех мячей. Сколько процентов составляют оставшиеся мячи? Найти числа, 20 %, 25%, 50% которых равны 60 Сколько процентов от 1 м составляет 4 дм ? В парке растет 600 деревьев. Сколько деревьев составляют от всех деревьев: 30 % |
| КАРТОЧКА № 2.2 Девочки составляют 78% всех участников соревнований. Сколько процентов всех участников составляют мальчики? Найти числа, 20 %, 25 %, 50 % которых равны 40. Сколько процентов от 1 м составляет 5 дм ? В парке растет 600 деревьев. Сколько деревьев составляют от всех деревьев: 25 % ? |
| КАРТОЧКА № 2.3 В автопарке машины марки «Жигули» составляют 23% всех машин. Сколько процентов всех машин составляют остальные машины? Найти числа, 20 %, 25 %, 50 % которых равны 20. Сколько процентов от 1 м составляет 2 дм ? В парке растет 600 деревьев. Сколько деревьев составляют от всех деревьев: 20 % ? |
| КАРТОЧКА № 3.1 Укажите запись в виде десятичной дроби 3 % Ответы: А) 0, 3 Б) 0,003 В) 0, 03 Г) 300 Что меньше: четверть дороги или 20 % дороги? Найдите 45 % от 6 км Вспахали 30 % поля, что составило 48 га. Найдите площадь всего поля. |
| КАРТОЧКА № 3.2 Укажите запись в виде десятичной дроби 7 % Ответы: А) 0, 7 Б) 0,007 В) 0, 07 Г) 700 Что больше: 53% населения или половина населения? Найдите 64 % от 5 кг. Посадили 60 саженцев, что составило 20 % всех саженцев. Сколько всего саженцев? |
| КАРТОЧКА № 3.3 Укажите запись в виде десятичной дроби 9 % Ответы: А) 0, 9 Б) 0,009 В) 0, 09 Г) 900 Что меньше: четверть суши или 24 % суши? Найдите 70 % от 85 т. Отремонтировали 40 % дороги, что составило 160 м. Найдите длину всей дороги. |
| |
| КАРТОЧКА № 4.1 Запишите в виде процентов числа 0,084; 0,84; 8,4. Запишите в виде обыкновенной и десятичной дробей 3%, 17%, 131%. Найти 1 % от 5 м, 50 м, 500 м. Морская вода содержит 6 % соли. Сколько морской воды надо взять, чтобы получить 42 кг соли? |
| КАРТОЧКА № 4.2 Запишите в виде процентов числа 0,032; 0,32; 3,2 Запишите в виде обыкновенной и десятичной дробей 7%, 13 %, 123%. Найти 1 % от 3 м, 30 м, 300 м. Медная руда содержит 8 % меди. Сколько руды надо взять, чтобы получить 18 т меди? |
| КАРТОЧКА № 4.3 Запишите в виде процентов числа 0,056; 0,56; 5,6. Запишите в виде обыкновенной и десятичной дробей 9%, 19%, 191%. Найти 1 % от 7 м, 70м, 700м. Руда содержит 70 % железа. Сколько надо взять руды, чтобы получить 42 т железа? |
| КАРТОЧКА № 5.1 Переведите в проценты 0,06; 1,17;  . . Найдите 8 % от числа 16, 75, 400. Найдите число, если 36 % этого числа равны 180. Сплав содержит 35 % железа. Сколько килограммов железа содержится в 970 кг сплава? |
| КАРТОЧКА № 5.2 Переведите в проценты 0,05; 1,24;  . . Найдите 9 % от числа 18, 24, 300. Найдите число, если 24 % этого числа равны 60. Сплав содержит 6 % олова. Сколько килограммов олова содержится в 520 кг сплава? |
| КАРТОЧКА № 5.3 Переведите в проценты 0,03; 1,46;  . . Найдите 6 % от числа 12, 75, 400. Найдите число, если 28 % этого числа равны 126. Сплав содержит 8 % железа. Сколько тонн меди содержится в 260 т сплава? |
Тестовые задания
-
1. 3% - это
1) 0,3
2) 0,03
3) 0,0003
4) 3
-
0,273 – это
1) 27,3%
2) 2,73%
3) 273%
4) 0,273%
-
20% избирателей – это
1) двадцатая часть избирателей
2) половина избирателей
3) четверть избирателей
4) пятая часть избирателей
-
А4. При помоле пшеницы получается 80% муки. Сколько муки получится из 90 тонн пшеницы?
1) 112,5 т.
2) 10 т.
3) 72 т.
4) 7200 т.
-
А5. За первую половину урока Петя выполнил 60% задания, а за вторую – 27%. Сколько процентов задания не выполнил Петя?
1) 13%
2) 33%
3) 23%
4) 87%
6. Найдите длину пути,75% которого равны 30 км
1) 35
2) 75
3)40
4)45
7. На полке 60 книг. Сколько книг составляет 20% этих книг?
1) 12
2) 15
3)17
4) 21
8. Сколько получится, если к 17% числа 810 прибавить 146?
1)246,6
2) 1377,7
3)283,7
4)270
9. Закончите предложение 25% класса – это:
1) десятая часть класса;
2) четверть учеников класса;
3) пятая часть класса;
4) двадцать пятая часть класса
10. Закончите предложение 1/5- это:
1) 20%
2) 0,2%
3)2 %
4) 0,02%
11.Найди число, если 5% его равно 240.
1) 4000
2) 4200
3)4800
4) 4600
12.Найди 15% от 300.
1) 55
2) 65
3)85
4) 45
13.Площадь поля 120 га. Пшеницей засеяно 45% поля. Какую площадь занимают посевы пшеницы?
1) 54га
2) 45га
3)56га
4) 64га
14. В библиотеке 16% всех книг – для детей. Сколько книг в библиотеке, если книг для детей в ней 720?
1) 4500
2) 4600
3)4800
4) 4700
15.Смешали 6кг сушеных яблок и 9 кг сушеных груш. Сколько процентов полученной смеси составляют яблоки?
1) 35%
2) 25%
3)20%
4) 40%
16. Из 76 м² площади квартиры кухня занимает 12 %. Найти площадь кухни.
1) 12, 08 м²
2) 24, 24 м²
3) 36, 4 м²
4) 9,12 м²
17. Содержание песка в земляной смеси составляет 20 %. Какова масса земляной смеси, если песка в ней 34 кг ?
1) 34 кг
2) 170 кг
3) 210 кг
4) 17 кг
18.Туристу нужно пройти 80 км. К концу первого дня он уже прошел 20 км. Сколько процентов пути прошел турист?
1) 25 %
2) 20 %
3) 40%
4) 10%
19. Сравните: 2% от 6 и 6% от 2
1) 2% от 6
2) 2% от 6 6% от 2
3) 2% от 6 = 6% от 2
4) сравнить нельзя
20. В сплаве есть медь, содержание которой составляет 25 %. Сколько килограммов меди содержится в сплаве массой 76 кг?
1) 38 кг
2) 19 кг
3) 7, 6 кг
4) 18 кг
21. Сколько страниц в книге, если рассказ в 12 страниц составляет 15 % книги?
1) 8 страниц
2) 36
3) 80
4) 64
22. Ученик решил 17 задач из 68. Сколько процентов задач он решил?
1) 15 %
2) 20 %
3) 40%
4) 25 %
23. Сравните: 15 % от 40 и 40 % от 10
1) 15% от 40
2) 15 % от 40 40% от 10
3) сравнить нельзя
24. Найдите 70% числа, 25% которого равно 40.
1) 112
2)120
3)102
4)160
25. Сколько квадратных метров в 24 % от 3 га
1) 800 м
2)7200м
3)4800м
4)250м
Заключение.
Данное практическое пособие позволит развить и закрепить навыки решения задач по теме: «Проценты» у учащихся 5-6 классов, может быть интересно учащимся, увлеченным математикой, а также полезно выпускникам школ и абитуриентам при подготовке к экзаменам. В дальнейшем на факультативных и кружковых занятиях возможны изучение вопроса применения процентов в экономике, в банковском деле. Можно провести сравнительный анализ банковских процентных ставок по потребительским кредитам и ипотечному кредитованию населения.
Литература.
1. .Быков А.А. и др В помощь поступающим в ГУ — ВШЭ, Математика, М: ГУ-ВШЭ, 2004
2.Денищева Л.О., Глазков Ю.А. и др., Учебно-тренировочные материалы для подготовки к ЕГЭ. Математика, М: Интеллект- Центр, 2003.
3. Потапов М.К., Олехник С.Н., Нестеренко Ю.В., Конкурсные задачи по математикеМ: Наука, 1992.
4. Семенко Е.А. и др., Готовимся к ЕГЭ по математике, Краснодар, Просвещение-Юг, 2005.
5. Алгебра, 9, под ред. Теляковского С.А., М: Просвещение, 2001
6. Алгебра и начала анализа, 10-11, под ред. Колмогорова А.Н., М: Просвещение, 2003.
7. Математика. Контрольные измерительные материалы единого государственного экзамена в 2004 г. М: Центр тестирования, 2004.
8. Экзаменационные материалы для подготовки к единому государственному экзамену. ЕГЭ 2006, М: Центр тестирования, 2005.
[1] «Математика, 5», Виленкин Н.Я. и др., «Мнемозина», 2003, с. 337
[2] «Алгебра, 9», под ред. Теляковского С.А., М: Просвещение, 2001, с.215, 223
[3] «Алгебра и начала анализа, 10-11», под ред. Колмогорова А.Н., М: Просвещение, 2003, с.306,330.
[4] «Учебно-тренировочные материалы для подготовки к ЕГЭ. Математика», Денищева Л.О., Гдазков Ю.А. и др., М: Интеллект- Центр, 2003.
«Математика. Контрольные измерительные материалы единого государственного экзамена в 2004 г.» М: Центр тестирования, 2004.
«Экзаменационные материалы для подготовки к единому государственному экзамену. ЕГЭ 2006», М: Центр тестирования, 2005.
[5] «Конкурсные задачи по математике», Потапов М.К., Олехник С.Н., Нестеренко Ю.В., М: Наука, 1992, с330-332.
«В помощь поступающим в ГУ — ВШЭ, Математика», Быков А.А. и дрМ: ГУ-ВШЭ, 2004, с 53-64
«Готовимся к ЕГЭ по математике», Семенко Е.А. и др., Краснодар, Просвещение-Юг, 2005, с. 46-51