Муниципальное бюджетное общеобразовательное учреждение основная общеобразовательная школа №1 г.Слюдянка
МЕТОДИЧЕСКОЕ ПОСОБИЕ
ОБУЧЕНИЕ МЕТОДУ ПЛОЩАДЕЙ ОБУЧАЮЩИХСЯ 9 КЛАССОВ НА ЭЛЕКТИВНОМ КУРСЕ
Составитель: Еремина Дарья Алексеевна,
учитель математики
Слюдянка 2022
СОДЕРЖАНИЕ
Введение 3
Глава 1. ПОДХОД К ПРОБЛЕМЕ РЕШЕНИЯ ЗАДАЧ С ИСПОЛЬЗОВАНИЕМ МЕТОДА ПЛОЩАДЕЙ 6
1.1.Суть, определение метода площадей 6
1.2. Основные свойства площадей 9
1.3. Решение опорных задач методом площадей……………………...……13
1.3. Сравнительный анализ школьных учебников математики…………….16
1.4. Определение элективного курса математики…………………………...17
Глава 2. ОБУЧЕНИЕ МЕТОДУ ПЛОЩАДЕЙ ОБУЧАЮЩИХСЯ 9 КЛАССОВ НА ЭЛЕКТИВНОМ КУРСЕ………………………………………19
2.1. Разработка приемов использования метода площадей………………..19
2.2 Содержание занятий по теме: «Метод площадей»…………………….20
2.2.1. Тематическое планирование…………………………..…………20
2.2.2. Занятие 1 ………………………………………………………….23
2.2.3. Занятие 2…………………………………………………………..32
2.2.4. Занятие 3…………………………………………………………..37
2.2.5. Занятие 4…………………………………………………………..44
2.2.6. Занятие 5…………………………………………………………..48
2.2.7. Итоговая контрольная работа………………………………….53
Заключение 55
Список литературы 56
Введение
Геометрия – это математическая область научного знания, которая занимается расчетом форм, расположенных на плоскости и в пространстве. Наука геометрия, как и любая математическая наука, анализирует объекты, которые представлены в реальном мире. При этом геометрия, хотя и относится к естественнонаучной сфере, существенно отличается от таких наук, как химия, биология, экономика, география и др. Главное различие состоит в том, что геометрия (да и все другие математические науки) строит абстрактную модель какого-либо объекта, не вдаваясь в его состав и содержание. Использование геометрической абстракции дает возможность при решении геометрических задач использовать метод дедукции, другими словами, на основании имеющихся аксиом, законов и свойств получать новый геометрический закон или свойство. При этом другие наук естественнонаучного толка зачастую используют методы индукции, при котором из ряда частных свойств исследуемого объекта делается обобщение, которое в дальнейшем распространяется на другие аналогичные объекты.
Геометрическая наука использует для решения своих задач широкий спектр методов и научных подходов, к которым относят синтетический, векторно-координатный, преобразовательный метод и метод ключевых задач. В каждой группе методов можно выделить алгебраические и геометрические методы. Из группы геометрических методов можно выделить метод треугольников, метод площадей, метод дополнительных фигур, координатно-векторный метод и прочие. В практике школьного курса геометрии наибольшую популярность, кроме синтетического метода, имеет координатно-векторный метод, так как он основан на представлении объекта исследования в координатном двумерном или трехмерном виде.
К сожалению, нет одного, подходящего метода для решения всех задач на определение площади плоской фигуры, однако, в геометрии есть различные математические инструменты, которые подходят к определенному блоку задач. Кроме того, важно отметить, что в ряде случаев для решения геометрической задачи требуется расчет площади фигуры, хотя в соответствии с условием такой задачи нужно найти другую величину. Таким образом, можно утверждать, что в геометрии существует метод площадей, позволяющий решать задачи определенного типа.
Отметим, что в научно-исследовательских и методических работах различных ученых, методологов и исследователей достаточно широко применяется метод площадей. При этом проведенный анализ таких работ позволяет утверждать, что при широкой практической освещенности этого метода его теоретическая составляющая рассмотрена слабо. Кроме того, отсутствует системный подход при раскрытии методических вопросов по обучению школьников рассматриваемому методу.
Объектом работы является математический метод площадей, который используется при решении задач на уроках геометрии в 9 классе.
Предмет работы – обучение методу площадей при решении задач в 9 классе.
Цель – разработка модуля элективного курса для обучения применению метода площадей к решению задач в 9 классе.
Задачи. Для достижения поставленной цели необходимо решить следующие задачи:
-
Анализ учебной и учебно-методической литературы по теме исследования.
-
Описание теоретического содержания элективного курса по обучению применению метода площадей.
-
Разработка практического содержания модуля элективного курса.
-
Создание содержания занятий элективного курса
Методы:
В процессе написания представленной работы были использованы различные методы исследования и научного познания, в том числе:
1) анализ и сравнение методической и учебной литературы;
2) разработка дидактических материалов практического и теоретического характера.
Глава 1. ПОДХОД К ПРОБЛЕМЕ РЕШЕНИЯ ЗАДАЧ С ИСПОЛЬЗОВАНИЕМ МЕТОДА ПЛОЩАДЕЙ
1.1 Суть, определение метода площадей
Характеристика метода.
Суть метода площадей состоит в том, что, произведя вычисление площади фигуры или ее составляющих, можно найти закономерность, описывающую характеристики исследуемого объекта, что в результате поможет получить ответ на вопрос, поставленный в геометрической задаче.
При этом метод площадей позволяет не только найти неизвестную изначально площадь фигуры, но и ответить на другие вопросы геометрической задачи, напрямую не связанные с этой геометрической характеристикой объекта исследования.
Далее рассмотрим перечень стандартных задач, в которых находит свое применение метод площадей. В процессе решения таких задач будет сделан вывод о видах и типах геометрических задач, в который рассматриваемый метод находит свое применение. Основные свойства данного метода, при накоплении практических навыков и теоретических знаний о методе площадей, по необходимости будут уточняться.
Суть данного метода состоит в том, что искомая величина входит в формулу площади фигуры и выражается из этих формул разными независимыми способами, впоследствии находится из уравнения [2].
Основополагающие понятия: уравнение, свойства площади (аддитивность и инвариативность), площадь и т.д.
Деятельностная сторона метода:
-
Нахождение площади фигуры различными способами;
-
Применение свойств площадей;
-
Составление и решение уравнения;
-
Соотнесение результата с исходными данными.
Форма метода, (зависят от типов задач, решаемых методом площадей) [1]:
-
Задачи на вычисление:
-
Известна площадь исходной фигуры (или её частей), необходимо найти площадь другой фигуры ( или её частей);
-
Известны элементы фигуры, найти её площадь;
-
Известна площадь фигуры, найти её элементы;
-
Известны элементы фигуры, найти другие её элементы.
-
Задачи на доказательство:
О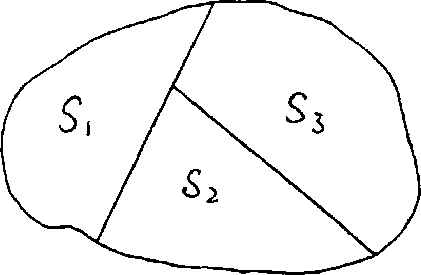
Рис. 1
дин из подходов, который используется при реализации метода площадей, заключается в том, что анализируемую фигуру в соответствии с условием задачи или по самостоятельному решению нужно разбить на несколько составных частей, при этом площадь целой фигуры будет равна сумме площадей фигур, образованных в процессе разделения изначальной фигуры :
S=S1+S2+S3
Такое свойство площади называют свойством аддитивности.
Таким образом, получаем уравнение, в котором с одной стороны из характеристик фигуры записывается формула для расчета площади целой фигуры, а с другой – сумма площадей ее поставляющих на основании их геометрических характеристик. При этом в данном уравнении должно соблюдаться условие одной переменной, в качестве которой может выступать длина стороны или отрезка.
Кроме того, в качестве примера можно рассмотреть задачу нахождения стороны или высоты треугольника. Как известно площадь такой фигуры может быть найдена несколькими способами. Если составить равенство, в левой части которого записать одну формулу площади, а в правой – другую, то из полученного равенства можно будет выразить неизвестную характеристику, например, длину стороны или высоту треугольника [3].
1.2. Основные свойства площадей
Свойство №1
При перемещении вершины заданного треугольника по прямой линии, параллельной его основанию, площадь вновь образованных треугольников не меняется и остается равной площади исходной фигуры.
Д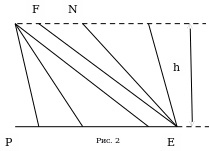 оказательство:
оказательство:
Для доказательства возьмем два произвольных треугольника (рис.2), например, PFE и PNE, которые имеют одно и тоже основание РЕ. Их высоты равны, так как
прямые AC и BD параллельны друг другу, примем длину высоты, равную h. Расчет площади треугольника производится по формуле 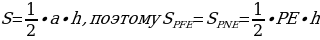 [1,5].
[1,5].
Свойство №2
Если два треугольника имеют одинаковые высоты, то отношение их площадей равно отношению длин оснований (сторон, на которые опущены эти высоты).
Д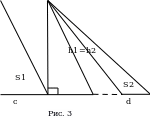 оказательство:
оказательство:
Пусть 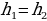 в двух треугольниках (Рис.3) с основаниями a и b. Рассмотрим отношение площадей этих треугольников
в двух треугольниках (Рис.3) с основаниями a и b. Рассмотрим отношение площадей этих треугольников
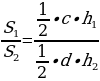
упростив, получим 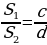 [5].
[5].
Свойство №3
Если два треугольника имеют общий угол, то их площади относятся как произведение сторон, заключающих этот угол.
Д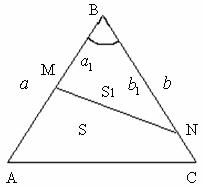 оказательство:
оказательство:
Рассмотрим треугольники ABC и MBN с общим углом B (Рис.4), где AB = a, BC = b, MB = a1 и NB = b1. Пусть 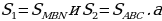
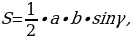 рассмотрим отношение площадей треугольников АВС и MBN.
рассмотрим отношение площадей треугольников АВС и MBN.
Т
Рис. 4
огда
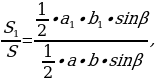
упростив получим
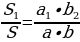
[5].
Свойство №4
Отношение площадей подобных треугольников равны квадрату коэффициента подобия [5].
Д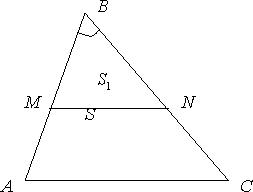 оказательство:
оказательство:
Рассмотрим треугольники ABC и MBN (Рис.5). Пусть AB = k∙MB, BC = k∙NB и ∠ABC=∠MBN.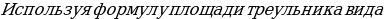
Рис. 5
рассмотрим отношение подобных площадей треугольников АВС и MBN. В результате получаем, что
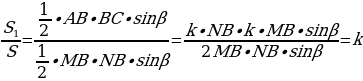
.
Свойство №5
Медиана треугольника делит его на две равновеликие части [5].
Д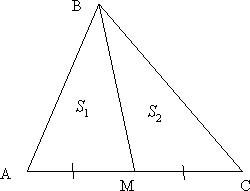
Рис. 6
оказательство:
Рассмотрим треугольник ABС (Рис.6). Пусть ВМ - медиана, тогда 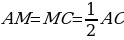 . Медиана делит треугольник на два с одинаковой высотой. Найдем площади треугольников АВМ и МВС по формуле
. Медиана делит треугольник на два с одинаковой высотой. Найдем площади треугольников АВМ и МВС по формуле  . Получим
. Получим 
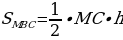 значит
значит
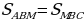 .
.
Свойство №6
Медианы треугольника делят его на три равновеликие части [5].
Д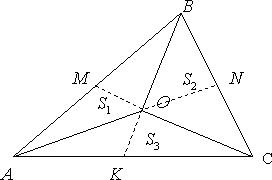
Рис. 7
оказательство:
Рассмотрим треугольник ABC (Рис.7). Проведем медианы из всех вершин, которые пересекаются в точке O. Получим треугольники AOB, BOC, AOC. Пусть их площади соответственно равны 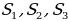 , а площадь треугольника АВС равна S. Рассмотрим треугольники АВК и
, а площадь треугольника АВС равна S. Рассмотрим треугольники АВК и
СВК, их площади равны, так как ВК – медиана. В треугольнике АОС, ОК – медиана, значит площади треугольников АОК и СОК равны. Отсюда следует, что 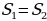 , аналогично доказывается, что
, аналогично доказывается, что 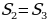 и
и 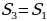 .
.
Свойство №7
Средние линии треугольника площади S отсекают от него треугольники площади 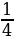 S [5].
S [5].
Д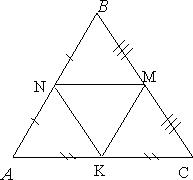
Рис. 8
оказательство:
Рассмотрим треугольник ABC (Рис.8). NM - средняя линия в треугольнике и она равна половине основания AC. Если 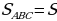 , то
, то 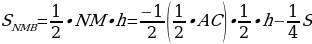 . Аналогично можно доказать, что площади всех треугольников равны одной четвертой части площади треугольника АВС.
. Аналогично можно доказать, что площади всех треугольников равны одной четвертой части площади треугольника АВС.
Свойство №8
Медианы треугольника делят его на 6 равновеликих частей [5].
Д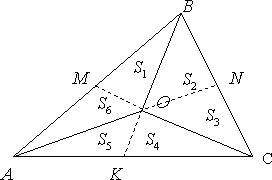
Рис. 9
оказательство:
По свойству №7 площади треугольников AOB, BOC, AOC равны (Рис.9). По свойству №5 площади треугольников AOM, BOM равны. Значит 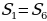 . Аналогично
. Аналогично 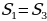 . Если
. Если  и так далее, в результате получим, что все шесть треугольника имеют равные площади и они составляют шестую часть от площади треугольника АВС.
и так далее, в результате получим, что все шесть треугольника имеют равные площади и они составляют шестую часть от площади треугольника АВС.
1.3. Решение опорных задач методом площадей.
Для того чтобы начать осваивать метод площадей, необходимо изучить решения, так называемых, опорных задач.
Е. Е. Овчинникова в своей работе [16] разделяет задачи, в которых применяется метод площадей, на 3 вида, а именно:
-
Использование двух разных способов для нахождения площади фигуры;
Задача 1. Задан треугольник АВС. К стороне СВ проведена высота АК, а к стороне АВ высота СН. Длина АВ составляет 9, СВ – 6, а СН – 4. Найдите длину высоты АК.
Решение:

Рис. 13
Найдем площадь треугольника (рис. 13), используя две формулы, и приравняем их:
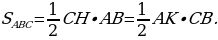
Тогда, 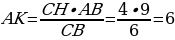
-
Задачи на применение свойства аддитивности;
Задача 2. На сторонах АВ, ВС и АС Δ ABC отмечены точки М, N и К таким образом, что выполняются следующие соотношения:
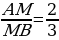
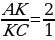
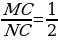
Необходимо рассчитать соотношение, в котором отрезок МК делит отрезок AN .
Решение:
О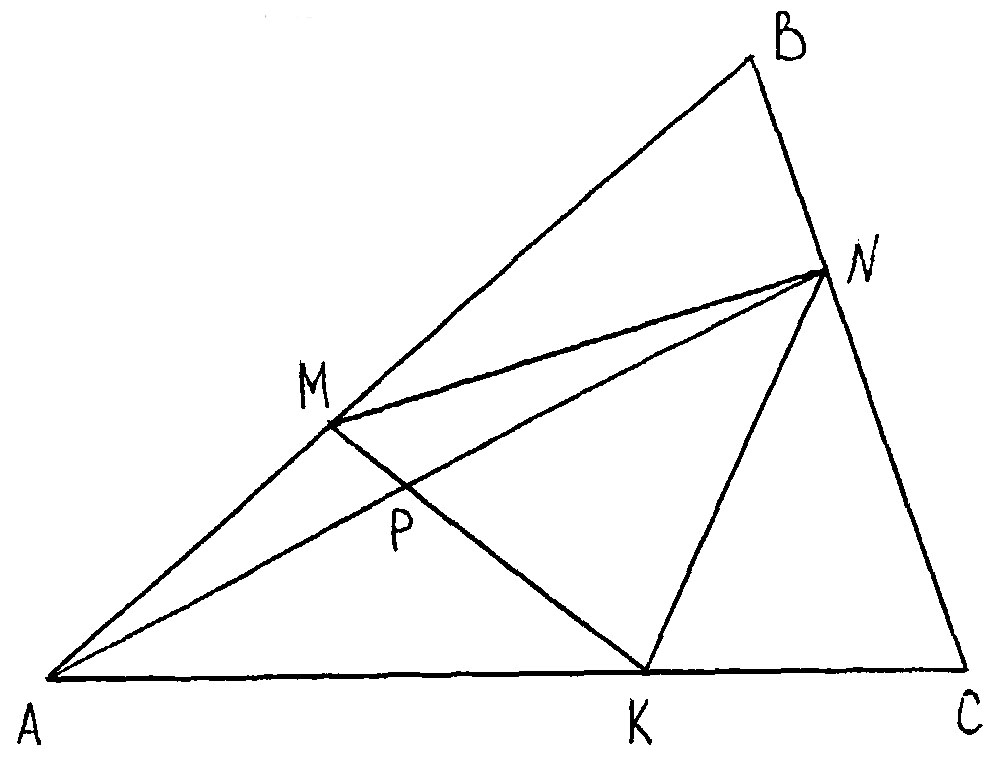
Рис. 14
бозначим в качестве точки пересечения отрезков
МК и
AN точку
P (Рис.14)
. Далее возьмем к рассмотрению получившийся четырёхугольник
AMNK. В соответствии со свойством 3,
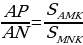
. На основании площади Δ
ABC найдем площади Δ
AMK и Δ
MNK . Таким образом, площадь Δ
MNK можно рассчитать на базе следующего соотношения:
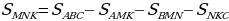 (1).
(1).
В Δ AMK и Δ ABC есть общий угол, поэтому можно отметить:
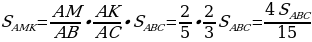
Аналогично находим
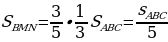
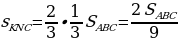
Подставляя в (1), получаем, что
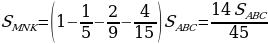
Следовательно,
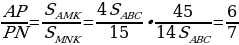
-
Задачи на применение свойств отношения площадей.
Задача 3. Дана трапеция ABCD, её основания ВС и AD равны 2 и 6 соответственно. Диагонали BD и АС пересекаются в точке О. Точка Р – середина OD. 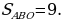 Найдите площадь четырехугольника АВСР.
Найдите площадь четырехугольника АВСР.
Р
B
C
ешение:
п
O
усть

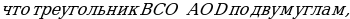
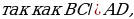
P
угол ВСА = углу САD как накрест лежащие и угол ВОС = углу AOD как вертикальные.
С
Рис. 15
D
A
ледовательно,
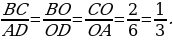
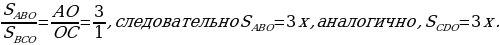
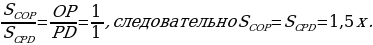
Площади подобных треугольников относятся как коэффициент подобия в квадрате, следовательно, 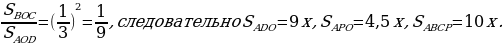 Так как 3х = 9, то х = 3 и, следовательно,
Так как 3х = 9, то х = 3 и, следовательно, 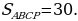
Ответ:30.
1.4. Сравнительный анализ школьных учебников математики.
В процессе написания представленной работы была проведена аналитическая работа, которая состояла в сравнении материалов, размещенных в теоретических источниках и практических решебниках на использование расчета площади плоских фигур и метода площадей. Сравнение производилось по следующим тематикам:
1. Измерение площади;
2. Расчет площади;
3. Метод площадей.
Целью аналитической работы являлись ответы на такие вопросы, как «Представлено ли описание данных тем?» и «Как описаны эти темы?»
Анализ проведен на основе двух учебников по геометрии: учебник Шлыкова В.В. , учебник Латотина Л.А., Чеботаревского Б.Д. и учебник Атанасян Л.С.
Изучение понятия «Площадь плоских фигур» в представленных материалах происходит в различные периоды школьной программы. В учебных материалах Шлыкова В.В. этой теме посвящено несколько уроков в начале 9 класса, у Атанасян Л.С. в середине 8 класса, в-третьем же случае в конце 8 и начале 9 класса. Отметим, что у Латотина Л.А., Чеботаревского Б.Д. тема «Площадь многоугольников» рассматривается только в последней главе «Четырехугольники», в то время как у Шлыкова В.В. и Атанасян Л.С. данной теме посвящено 4 параграфа, которые вынесены в отдельную главу «Площадь многоугольников».
Понятие «Площадь» во всех материалах вводится на основании примеров из жизни, что крайне важно, так как упрощает понимание нового материала. Так как учащиеся ранее на уроках математики касались понятия площади, то авторы учебников предлагают им самостоятельно привести жизненные примеры. В рассматриваемых учебных пособиях понятию «площадь» дается четкое определение, в котором указываются все ее ключевые характеристики и аспекты.
Измерение же площади в учебниках рассматривается по-разному. Латотин Л.А., Чеботаревский Б.Д. не рассматривают подробно данную тему, Шлыков В.В. же и Атанасян Л.С. дает подробное описание этого процесса.
Анализируя тему расчета площади плоских фигур, стоит отметить, что во всех учебниках этому вопросу посвящено достаточно много материалов: приводятся конкретные формулы, доказывается их состоятельность, описываются единицы расчета и т. д.
Если рассматривать практический материал в анализируемых учебниках, то можно отметить, что Латотин Л. А., Чеботаревский Б.Д. и Атанасян Л.С. предлагают разные по сложности задачи, которые должен уметь решать каждый школьник после прохождения темы «Площадь». Шлыков В. В. в своем учебнике предлагает к обязательному решению только простейшие задачи, а сложные рекомендуются к решению только по желанию учащегося (или усмотрению учителя). Кроме того, в данных учебных материалах содержится всего по 2-3 задачи на метод площадей, что явно недостаточно.
1.5. Определение элективного курса математики
Под понятием элективного курса следует понимать образовательный курс по выбору учащегося. Такие курсы являются новым элементом учебной программы, который в старших классах доказывает свою эффективность при профессиональном самоопределении школьника. Элективные курсы для учащихся старших классов должны проходить обязательно. Это и отличает их от факультативных курсов, посещение которых производится по желанию школьников [10].
Ключевая цель использования элективных курсов заключается в формировании устремлений школьников в дальнейшем заниматься определенной деятельностью или, другими словами, профессиональная ориентация.
Для курса школьной математики также предусмотрены элективные курсы следующих видов:
- продвинутый уровень, на этом уровне рассматриваются частные математические вопросы, решение которых выходит за рамки школьной программы;
- повышенный уровень, на котором производится детальный разбор тем, которые как могут входить в школьный курс, так и не рассматриваться в нем;
- прикладной уровень, на этом уровне рассматриваются прикладные задачи, в которых могут найти свое применение математические методы и инструменты;
- одинарный уровень, на котором рассматривается конкретная математическая задача.
Целями математических элективных курсов являются:
- формирование прочных знаний в сфере математики у школьников;
- тренировка и развитие математической логики у обучающихся;
- понимание сущности и прикладного значения поиска решения алгебраических и геометрических задач.
Разработка и внедрение в практическое использование элективного курса по математике для школьников 9-х классов позволит повысить их уровень подготовленности к сдаче ОГЭ, а также развить их знания, навыки и умения решения сложных математических задач.
Элективный курс школьной математики, посвящённый изучению методов и способов решения задач, нацеленный на успешную сдачу выпускниками школы ОГЭ, является в настоящее время наиболее востребованным. Составной частью такого курса может быть модуль по обучению старшеклассников использованию метода площадей при решении задач, создание которого является целью разрабатываемой ВКР.
Глава 2. ОБУЧЕНИЕ МЕТОДУ ПЛОЩАДЕЙ ОБУЧАЮЩИХСЯ 9 КЛАССОВ НА ЭЛЕКТИВНОМ КУРСЕ 2.1. Разработка приемов использования метода площадей.
В курсе геометрии существует множество приемов для применения к решению многих задач. Но для решения задач на нахождение площади многоугольников универсального метода нет. Мы можем пользоваться понятием «Площадь» даже в тех задачах, в которых нет упоминания площадей.
Изучение темы «Применение метода площадей при решении задач» рекомендуется после освоения учащимися материала курса планиметрии таких разделов как: «Площадь многоугольников».
Главной целью элективного курса должно быть формирование у школьников базовых представлений о методе площадей и навыков его использования при решении различных геометрических задач.
Для успешного изучения материала возможны различные формы работы с учащимися: лекционно – семинарские занятия, индивидуальные формы работы, при этом основной тип занятий – практические занятия.
Важно начинать знакомить с методом площадей с простейших задач, для формирования умений и навыков, которые помогут учащимся в решении более сложных задач. Учащиеся должны видеть применение метода от простейших до сложных задач. Сложность задач увеличивайте на основе темпа освоения материала.
Задача требует актуализации знаний через рассмотрение некоторых признаков данной фигуры, а затем на их основе выстраивается логическая последовательность мыслительных рассуждений по проверке рассматриваемой фигуры на наличие или отсутствие у нее основных признаков.
Ключевое свойство рассматриваемого метода – это использование такой характеристики геометрической фигуры, как площадь. Метод площадей позволяет на основании расчета площади объекта получить требуемую величину. В результате составляется уравнение, в которое входят формулы площади. И затем из этого уравнения находится неизвестная величина при помощи математических преобразований.
Если рассматривать применение метода площадей в виде конкретного алгоритма, то в него будут входить такие операции:
-
Выбираем фигуру или фигуры, для которых будем искать площадь;
-
Определяем формулы, на основании которых можно рассчитать площадь;
-
Записываем выбранные формулы с использованием искомого параметра;
-
Записываем уравнение, используя свойство аддитивности или приравнивая один расчет площади к другому (если рассматривается одна геометрическая фигура);
-
На основе математических операций выделяем неизвестную величину из уравнения и производим ее расчет на основании заданных по условию задачи величин [14].
Отметим тот факт, что задачи, которые решаются методом площадей, широко представлены на ЕГЭ по математике, поэтому рекомендуется на уроках геометрии данную тему рассматривать максимально широко, в том числе и с использованием элективного курса.
2.2. Содержание занятий «Метод площадей»
2.2.1. Тематическое планирование
На уроках геометрии уделяется недостаточно внимания целенаправленному обучению методу площадей. В учебниках данный метод рассматривается, как дополнение к главе. Зачастую, для экономии времени, учитель, подробно не рассматривает данную тему. Поэтому данная тема является обязательной для изучения на элективном курсе.
В разработанных занятиях представлено теоретическое и практическое содержание темы «Метод площадей». Занятия по данной теме рассчитаны на учащихся 9 классов. В рамках изучения данной темы рассмотрены различные типы задач, посвященные данной теме.
Цели занятий:
- освоить теоретическое и практическое содержание темы: «Метод площадей»;
- развивать умение применять знания курса на практике, при решении задач;
- отработать навык выполнения геометрических построений.
Задачи занятий:
- обеспечить наглядность, логическую строгость рассуждений и обоснованность выводов;
- создать условия для выдвижения различных гипотез при поиске решения задачи;
- развивать интерес и положительную мотивацию к изучению геометрии, создать условия для подготовки учащихся к успешному прохождению ОГЭ.
Основной тип занятий – практические занятия.
Для наиболее успешного изучения материала планируются различные формы работы с учащимися: лекционно – семинарские занятия, индивидуальные формы работы.
Содержательно – методическая часть: содержание занятий по теме «Метод площадей» планируется изучать согласно тематическому планированию (см. таблицу).
Тематическое планирование
Таблица 2
| № занятия | Содержание материала | Количество часов |
| 1 | Введение метода площадей. | 1 |
| 2 | Метод площадей и свойства 1-3. | 1 |
| 3 | Метод площадей и свойства 4-8. | 1 |
| 4 | Решение типовых задач из ОГЭ по теме Метод площадей | 2 |
| 5 | Итоговая контрольная работа по теме: «Метод площадей». | 1 |
| Итого: | 6 |
2.2.2. Занятие 1 по теме: «Метод площадей»
Занятие №1
Тема «Метод площадей (1 тип задач)»
Тип урока: комбинированный
Цели обучения:
Цель развития: формирование навыков работы с текстом, развитие внимания, памяти речи.
Цель воспитания: воспитание познавательной активности, культуры общения, ответственности.
Метод обучения: объяснительно – иллюстративный метод.
-
Подготовительный этап
Цель: актуализация знаний о понятии площадь многоугольников, вспомнить изученные формулы нахождения площади.
Приёмы обучения: предъявление обучающимся вопросов и заданий.
Учитель (У): Здравствуйте, ребята! Проверьте наличие на партах карандаша, ручки, линейки, циркуля, ластика, тетради и учебника. Присаживайтесь.
Обучающиеся (О): проверяют, садятся.
(У): Ребята, давайте вспомним что такое площадь многоугольников?
(О): Площадь многоугольников – это величина той части плоскости, которую занимает многоугольник.
(У): Верно. Давайте с вами вспомним, а сколько же формул нахождения площади многоугольников мы знаем? (учащиеся в парах опрашивают друг друга, 2 человека с обратной стороны доски записывают).
(У): Молодцы!
2. Мотивационный этап.
Цель: побуждение интереса к изучению метода.
Приём мотивации: показ необходимости знаний метода для решения задач.
(У): Сейчас давайте применим наши знания при решении задач (выдается индивидуальная работа на каждого учащегося).
Таблица 1.
| № | Задача | Решение |
| 1 | 
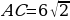 , угол , угол 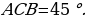
Н айти: айти:  |
|
| 2 |
Н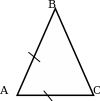 айти: айти:  |
|
| 3 |
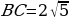 , угол , угол 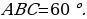
Найти: 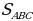 |
|
| 4 | 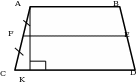
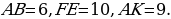
Найти: 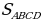 |
|
| 5 | 
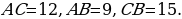
Н айти: айти:  |
|
| 6 |
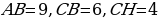 . .
Найти: 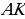 |
|
(У): Обсудим и проверим правильность решения данных задач (отвечают по 1).
(1 О): задача 1: 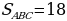 .
.
(2 О): задача 2: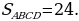
(3 О): задача 3: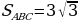 .
.
(4 О): задача 4: 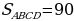 .
.
(5 О): задача 5: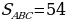 .
.
(У): Теперь давайте выполним задачу №6.
(О): Пытаются выполнить.
(У): Получилось решить?
(О): Нет.
(У): Как вы думаете, почему?
(О): Мы не знаем какого-то метода для решения 6 задачи.
3. Ориентировочный этап.
Цель: сформулировать метод.
Цель обучения: включение детей в доказательство выдвинутой гипотезы.
(У): Какова цель нашего урока?
(О): Мы должны найти какой-то метод, который поможет нам решить данную задачу.
(У): При решении задачи №6 у нас возникли трудности. Давайте попробуем вместе её разобрать. Для начала вспомним, а как мы можем найти площадь данного треугольника.
(О): 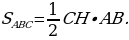
(У): Верно.
(О): Но, площадь данного треугольника мы ещё можем найти, как 
(У): Конечно, площадь треугольника АВС поменяется при изменении формулы?
(О): Нет, площадь останется неизменной.
(У): Верно, мы можем уровнять данные формулы? и выразить АК?
(О): Да (выполняют).
(У): А теперь давайте попробуем неизвестный элемент заменить на х и выразить его.
(О): (выполняют).
(У): Что у вас получилось?
(О): 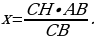
(У): Правильно, мы можем найти наш x?
(О): Да(выполняют).
(У): Что у вас получилось?
(О): 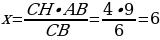
(У): Хорошо, правильно. При помощи чего мы смогли найти неизвестный элемент?
(О): Мы использовали 2 способа нахождения площади данной фигуры, затем выразили неизвестный элемент и нашли его значение.
(У): Про площадь что-то было дано в условии задачи?
(О): Нет.
(У): Так какой мы можем сделать вывод?
(О): Мы можем решить задачу, используя площадь, при этом в условии задачи про неё ничего не сказано.
(У): Верно, такой метод решения называется «Метод площадей».
(О): (записывают тему урока).
(У): Объяснение метода площадей:
Суть метода площадей состоит в том, что, произведя вычисление площади фигуры или ее составляющих, можно найти закономерность, описывающую характеристики исследуемого объекта, что в результате поможет получить ответ на вопрос, поставленный в геометрической задаче.
При этом метод площадей позволяет не только найти неизвестную изначально площадь фигуры, но и ответить на другие вопросы геометрической задачи, напрямую не связанные с этой геометрической характеристикой объекта исследования.
Данная задача демонстрирует задачи, при решении которых мы можем использовать метод площадей. Суть данного решения заключается в том, что мы:
-
Определяем формулы, на основании которых можно рассчитать площадь;
-
Записываем выбранные формулы с использованием искомого параметра;
-
Записываем уравнение приравнивая один расчет площади к другому;
-
На основе математических операций выделяем неизвестную величину из уравнения и производим ее расчет на основании заданных по условию задачи величин.
Далее рассмотрим перечень стандартных задач, в которых находит свое применение метод площадей.
4. Этап применения метода.
Цель: обучение применению метода площадей при решении задач.
(У): Ребята, давайте решим следующие задачи.
Задача 1. Катеты прямоугольного треугольника равны 3 и 4. Найти высоту, проведенную к гипотенузе данного треугольника.

Рис. 2
Решение:
По теореме Пифагора найдем гипотенузу данного прямоугольного (рис.2) треугольника: 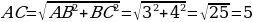
Площадь прямоугольного треугольника можно найти 2 различными способами: 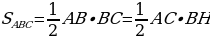 , из данного равенства выделим высоту:
, из данного равенства выделим высоту: 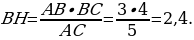
Ответ: 2,4.
Задача 2. Дана трапеция ABCD, её основания ВС и AD равны 2 и 6 соответственно. Диагонали BD и АС пересекаются в точке О. Точка Р – середина OD. 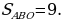 Найдите площадь четырехугольника АВСР.
Найдите площадь четырехугольника АВСР.
Р
B
C
ешение:
п
O
усть

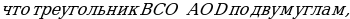
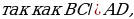
P
угол ВСА = углу САD как накрест лежащие и угол ВОС = углу AOD как вертикальные.
С
Рис. 3
D
A
ледовательно,
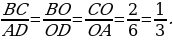
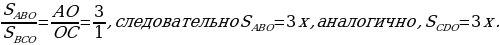
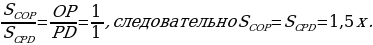
Площади подобных треугольников относятся как коэффициент подобия в квадрате, следовательно, 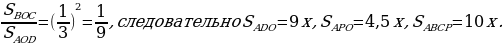 Так как 3х = 9, то х = 3 и, следовательно,
Так как 3х = 9, то х = 3 и, следовательно, 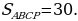
Ответ:30.
(У): Молодец. Приведем пример еще одной задачи.
Задача 3. Сторона основания равнобедренного треугольника равна 16, а боковые стороны равны 10. Найти высоту, приведенную к боковой стороне.

Рис. 3
Решение:
Проведем высоту ВК к основанию АС (рис.3), так как треугольник равнобедренный, то высота ВК является биссектрисой и медианной ( по свойству равнобедренного треугольника), следовательно АК=ЛС=8.
По теореме Пифагора найдем ВК: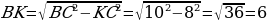
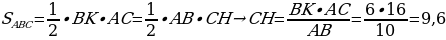
Ответ: 9,6.
Домашнее задание.
(У): Дома вам нужно повторить описание метода площадей, рассмотреть еще раз пройденные задачи.
Решить задачу: Сторона основания равнобедренного треугольника равна 6, а боковые стороны равны 5. Найти высоту, приведенную к боковой стороне.
Подведение итогов урока:
(У): Какой метод мы сегодня рассмотрели на уроке?
(О): Метод площадей .
(У): Сформулируйте особенности данного метода при решении задач.
(О): 1. Определяем формулы, на основании которых можно рассчитать площадь;
-
Записываем выбранные формулы с использованием искомого параметра;
-
Записываем уравнение приравнивая один расчет площади к другому;
-
На основе математических операций выделяем неизвестную величину из уравнения и производим ее расчет на основании заданных по условию задачи величин.
(У): Молодцы!
Занятие № 2
Тема «Метод площадей и свойства 1-3»
Тип урока: комбинированный
Цели урока:
Программа: «Геометрия. 9 класс»
-
Организационный этап.
Учитель приветствует класс, отмечают отсутствующих на уроке учащихся, проверяется готовность учеников к занятию.
-
Подготовительный этап
Проверка домашнего задания.
Учитель спрашивает желающих, кто готов выйти к доске и устно рассказать теоремы из домашнего задания.
-
Мотивационный этап
После проверки домашнего задания педагог пишет на доске и проговаривает вслух тему урока и кратко подводит учеников к тому, что сегодня будет рассматриваться и как это поможет в будущем.
-
Этап усвоения новых знаний
Объяснение метода площадей.
Суть метода площадей состоит в том, что, произведя вычисление площади фигуры или ее составляющих, можно найти закономерность, описывающую характеристики исследуемого объекта, что в результате поможет получить ответ на вопрос, поставленный в геометрической задаче.
При этом метод площадей позволяет не только найти неизвестную изначально площадь фигуры, но и ответить на другие вопросы геометрической задачи, напрямую не связанные с этой геометрической характеристикой объекта исследования.
Далее рассмотрим перечень стандартных задач, в которых находит свое применение метод площадей. В процессе решения таких задач будет сделан вывод о видах и типах геометрических задач, в который рассматриваемый метод находит свое применение. Основные свойства данного метода, при накоплении практических навыков и теоретических знаний о методе площадей, по необходимости будут уточняться.
После того, как учитель рассказал о том, что такое метод площадей, учащимся предлагается ответить на вопрос: «Как вы думаете, какие могут быть свойства у этого метода?»
После ответа учеников начинается изучение свойств метода площадей.
Первое свойство звучит следующим образом: если вершину треугольника передвигать по прямой, которая параллельна основанию, то площадь при этом не изменится.
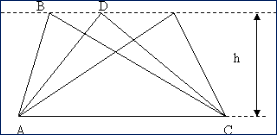
Рис. 16
Учитель: записываем доказательство данного свойства:
1. Мы рассмотрим треугольник ABC и треугольник ADC;
2. Они имеют общее основание и равные высоты;
3. Так как прямые AC и BD параллельные, то расстояние между ними равно h, - высоте треугольников ABC и ADC.
Второе свойство звучит так: если два треугольника имеют одинаковые высоты, то отношение их площадей равно отношению длин оснований, то есть сторон, на которые опущены эти высоты.
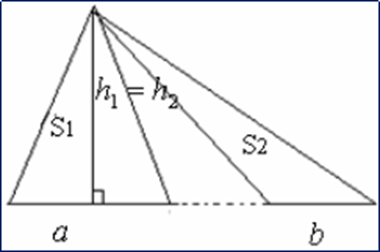
Рис. 17
Учитель: переходим к доказательству:
-
Пусть 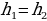 в двух треугольниках с основаниями a и b;
в двух треугольниках с основаниями a и b;
-
Рассмотрим отношение площадей этих треугольников и получим: 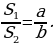
Третье свойство: Если два треугольника имеют общий угол, то их площади относятся как произведение сторон, заключающих этот угол.
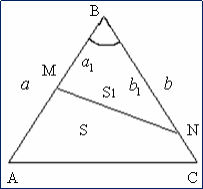
Рис. 18
Учитель: рассмотрим доказательство
-
Рассмотрим треугольник ABC и треугольник MBN;
-
Пусть 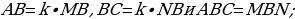
-
Используя формулу площади треугольника, получим: отношение подобных площадей треугольника ABC и треугольника MBN;
-
Тогда: 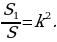
5. Этап закрепления новых знаний
Ученикам предлагается решить следующие задачи на применение изученных свойств:
З адача №1: через вершину треугольника ABC проведена прямая m, параллельная стороне АВ. Докажите, что все треугольники с вершинами на прямой m и основанием АВ имеют равные площади.
адача №1: через вершину треугольника ABC проведена прямая m, параллельная стороне АВ. Докажите, что все треугольники с вершинами на прямой m и основанием АВ имеют равные площади.
Рис. 18
Решение:
-
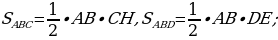
-
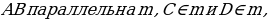
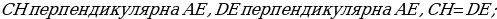
-
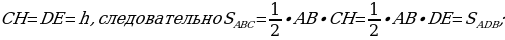
-
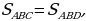 что и требовалось доказать.
что и требовалось доказать.
Задача 2. Треугольник ABC – равнобедренный. Точка М лежит на основании треугольника. KM и PM – перпендикуляры, опущенные на боковые стороны треугольника. Их длины равны соответственно n и m. 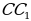 – высота, опущенная на боковую сторону. Докажите, что сумма длин n и m равна высоте
– высота, опущенная на боковую сторону. Докажите, что сумма длин n и m равна высоте 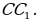
Доказательство:
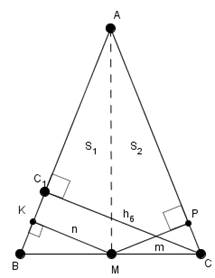
Рис. 19
Рассмотрим  : так как треугольник ABC равнобедренный, то основания у треугольников BAM и MAC – одинаковы, MK – высота первого треугольника, MP – высота второго треугольника. Имеем:
: так как треугольник ABC равнобедренный, то основания у треугольников BAM и MAC – одинаковы, MK – высота первого треугольника, MP – высота второго треугольника. Имеем:
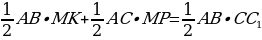
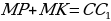
Ч.т.д.
6. Подведение итогов. Рефлексия. Домашнее задание.
Обсуждение с обучающимися результатов занятия, оценка ими новизны и полезности полученной информации, оценка доступности и качества усвоения новых знаний и умений, самооценка своих результатов.
Предлагается записать домашнее задание:
Выучить свойства метода площадей, их доказательства. Быть готовым к устному опросу.
Занятие № 3
Тема: «Метод площадей и свойства 4-8»
Тип урока: комбинированный
Цели урока:
Программа: «Геометрия. 9 класс»
-
Организационный этап.
Учитель приветствует класс, отмечают отсутствующих на уроке учащихся, проверяется готовность учеников к занятию.
-
Подготовительный этап
Проверка домашнего задания.
Учитель спрашивает желающих, кто готов выйти к доске и устно рассказать свойства метода площадей из домашнего задания.
-
Мотивационный этап
После проверки домашнего задания педагог пишет на доске и проговаривает вслух тему урока и кратко подводит учеников к тому, что сегодня будет рассматриваться и как это поможет в будущем.
-
Этап усвоения новых знаний
Свойство четвертое:
Отношение площадей подобных треугольников равны квадрату коэффициента подобия.
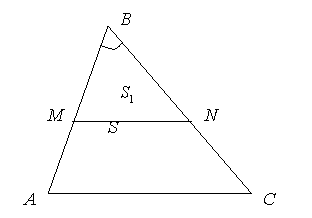
Рис. 20
Доказательство:
Рассмотрим треугольники ABC и MBN. Пусть AB = k∙MB, BC = k∙NB и ∠ABC=∠MBN.
 рассмотрим отношение подобных площадей треугольников АВС и MBN. В результате получаем, что
рассмотрим отношение подобных площадей треугольников АВС и MBN. В результате получаем, что 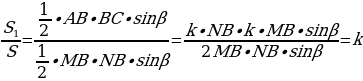 .
.
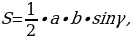 рассмотрим отношение подобных площадей треугольников АВС и MBN. В результате получаем, что
рассмотрим отношение подобных площадей треугольников АВС и MBN. В результате получаем, что 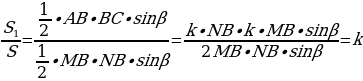
.
Свойство пятое:
Медиана треугольника делит его на две равновеликие части.
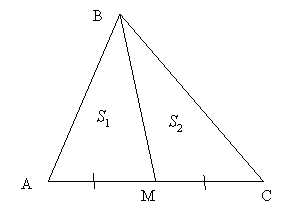
Рис. 21
Доказательство:
Рассмотрим треугольник ABС. Пусть ВМ - медиана, тогда
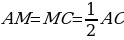 . Медиана делит треугольник на два с одинаковой высотой. Найдем площади треугольников АВМ и МВС по формуле
. Медиана делит треугольник на два с одинаковой высотой. Найдем площади треугольников АВМ и МВС по формуле 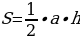 . Получим
. Получим 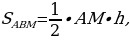
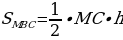 значит
значит
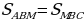 .
.
Свойство шестое:
Медианы треугольника делят его на три равновеликие части.
Рис. 22
Доказательство:
Доказательство. Рассмотрим треугольник ABC. Проведем медианы из всех вершин, которые пересекаются в точке O. Получим треугольники AOB, BOC, AOC. Пусть их площади соответственно равны 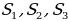 , а площадь треугольника АВС равна S. Рассмотрим треугольники АВК и
, а площадь треугольника АВС равна S. Рассмотрим треугольники АВК и
СВК, их площади равны, так как ВК – медиана. В треугольнике АОС, ОК – медиана, значит площади треугольников АОК и СОК равны. Отсюда следует, что 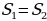 , аналогично доказывается, что
, аналогично доказывается, что 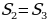 и
и 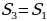 .
.
Свойство седьмое:
Средние линии треугольника площади S отсекают от него треугольники площади.
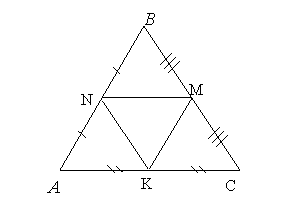
Рис. 23
Доказательство:
Рассмотрим треугольник ABC. NM - средняя линия в треугольнике и она равна половине основания AC. Если  , то
, то
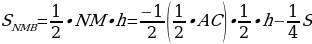 .
.
Аналогично можно доказать, что площади всех треугольников равны одной четвертой части площади треугольника АВС.
Восьмое свойство
Медианы треугольника делят его на 6 равновеликих частей.
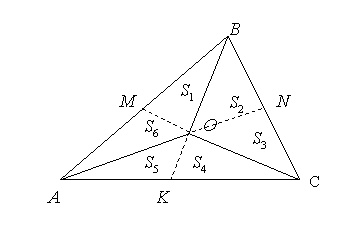
Рис. 24
Доказательство:
По свойству №7 площади треугольников AOB, BOC, AOC равны. По свойству №5 площади треугольников AOM, BOM равны. Значит 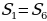 . Аналогично
. Аналогично 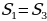 . Если
. Если  и так далее, в результате получим, что все шесть треугольника имеют равные площади и они составляют шестую часть от площади треугольника АВС.
и так далее, в результате получим, что все шесть треугольника имеют равные площади и они составляют шестую часть от площади треугольника АВС.
5. Этап закрепления новых знаний
Ученикам предлагается решить задачи письменно на оценку:
З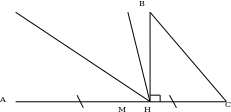 адача №1: Треугольник АВС разделен медианной МВ на два треугольника. Сравните площади этих треугольников.
адача №1: Треугольник АВС разделен медианной МВ на два треугольника. Сравните площади этих треугольников.
Рис. 25
Решение:
-
Проведем высоту ВН
-
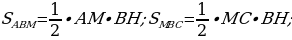
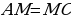 (так как ВМ – медианна)
(так как ВМ – медианна)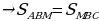 .
.
Задача №2: Точка пересечения медиан прямоугольного треугольника удалена от катетов на расстояния соответственно 3 и 4. Найдите расстояние от этой точки до гипотенузы (рис. 24).
Решение:
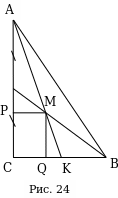
Поскольку медианы треугольника делятся точкой пересечения в отношении 2:1 , считая от вершины треугольника, то 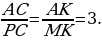
Поэтому 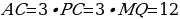
Аналогично 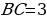 . Тогда
. Тогда 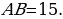
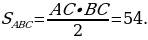
C другой стороны, 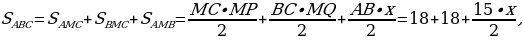 где х – искомое расстояние. Следовательно, х=2,4.
где х – искомое расстояние. Следовательно, х=2,4.
Задача для решения у доски:
Через точку K, данную на стороне AB треугольника ABC, проведите прямую так, чтобы она разделила площадь треугольника пополам.
Рис. 27
Решение:
-
Если точка K совпадает с серединой P стороны AB, то искомая прямая — это прямая CP, т. к. медиана треугольника делит его на два равновеликих треугольника;
-
Пусть точка K не совпадает с P;
-
Через точку P проведём прямую, параллельную CK;
-
Если K лежит между точками A и P, то проведённая прямая пересекает сторону BC;
-
Пусть M — точка пересечения, O — точка пересечения диагоналей CP и KM трапеции CKPM;
-
Тогда 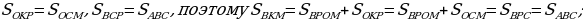
-
Следовательно, прямая KM делит треугольник ABC на две равновеликие части. Если K лежит между точками B и P, то прямая, проведённая через точку P параллельно CK, пересекает сторону AC.
6. Подведение итогов. Рефлексия. Домашнее задание.
Обсуждение с обучающимися результатов занятия, оценка ими новизны и полезности полученной информации, оценка доступности и качества усвоения новых знаний и умений, самооценка своих результатов.
Предлагается записать домашнее задание:
Выучить свойства метода площадей, их доказательства. Быть готовым к устному опросу.
Занятие № 4
Тема «Решение типовых задач из ОГЭ по теме Метод площадей»
Тип урока: применения знаний и умений
Цели урока:
-
Рассмотреть типовые задачи из заданий ОГЭ;
-
Понять, как решать типовые задачи из ОГЭ с помощью метода площадей
Программа: «Геометрия. 9 класс»
1. Организационный этап.
Учитель приветствует класс, отмечают отсутствующих на уроке учащихся, проверяется готовность учеников к занятию.
2. Подготовительный этап
Проверка домашнего задания.
Учитель спрашивает желающих, кто готов выйти к доске и устно рассказать свойства метода площадей из домашнего задания.
3. Мотивационный этап
После проверки домашнего задания педагог пишет на доске и проговаривает вслух тему урока и кратко подводит учеников к тому, что сегодня будет рассматриваться и как это поможет в будущем.
4. Этап закрепления полученных ранее знаний
Учитель пишет на доске условие задачи и предлагает желающему выйти её решить.
Задача 1. Стороны AC, AB, BC треугольника ABC равны  соответственно. Точка K расположена вне треугольника ABC, причём отрезок KC пересекает сторону AB в точке, отличной от B. Известно, что треугольник с вершинами K, A и C подобен исходному. Найдите косинус угла AKC, если ∠KAC 90°. Найти площадь треугольника АВС.
соответственно. Точка K расположена вне треугольника ABC, причём отрезок KC пересекает сторону AB в точке, отличной от B. Известно, что треугольник с вершинами K, A и C подобен исходному. Найдите косинус угла AKC, если ∠KAC 90°. Найти площадь треугольника АВС.
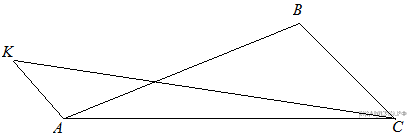
Рис. 28
Решение:
Рассмотрим подобные треугольники ABC и AKC, и установим соответствие между их углами. Против большей стороны всегда лежит больший угол, в треугольнике ABC это угол ABC в треугольнике КАС, в свою очередь, есть тупой угол КАС, и он является наибольшим, значит, ∠КАС = ∠АВС. Угол АСК заведомо не может быть равен углу АСВ, так как он составляет только его часть. Следовательно, угол АСВ равен углу АКС.
Найдём косинус угла АКС, используя теорему косинусов:
-
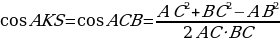 =
= 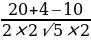 =
= 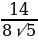 =
= 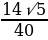 ;
;
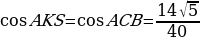 ;
;
-
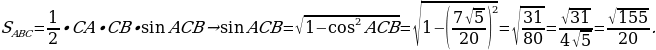
Ответ: 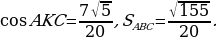
Учитель пишет на доске условие задачи и предлагает желающему выйти её решить.
Задача 2. В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника BOC.
Решение:
-
Проведём высоту MN так, чтобы она проходила через точку О. Угол BOM=NOD (по свойству вертикальных углов). Вспомним также, что диагонали делятся точкой пересечения пополам, следовательно, BO = OD;
-
Рассмотрим треугольники BOM и NOD, они прямоугольные, имеют равные углы и равные гипотенузы, следовательно, эти треугольники равны, а значит, равны отрезки MO и ON. Таким образом,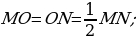
-
Площадь параллелограмм равна 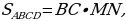 а площадь треугольника
а площадь треугольника 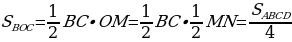 .
.
Задача 3. На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что отрезки BD и BE тоже равны. Докажите, что треугольник АВС — равнобедренный.
Решение:
-
По условию BD=BE, тогда треугольник BDE является равнобедренным;
-
Пусть угол при основании этого треугольника равен x, тогда угол BEC = углу BDA = 180 градусов – x;
-
Треугольники BEC и BDA равны по двум сторонам и углу между ними, поэтому AB=BC и треугольник ABC —равнобедренный;
З адача 4. Задан треугольник АВС. К стороне СВ проведена высота АК, а к стороне АВ высота СН. Длина АВ составляет 9, СВ – 6, а СН – 4. Найдите длину высоты АК (рис. 13).
адача 4. Задан треугольник АВС. К стороне СВ проведена высота АК, а к стороне АВ высота СН. Длина АВ составляет 9, СВ – 6, а СН – 4. Найдите длину высоты АК (рис. 13).
Рис. 29
Решение:
Найдем площадь треугольника, используя две формулы, и приравняем их:
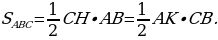
Тогда, 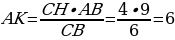
5. Подведение итогов. Рефлексия. Домашнее задание.
Обсуждение с обучающимися результатов занятия, оценка ими новизны и полезности полученной информации, оценка доступности и качества усвоения новых знаний и умений, самооценка своих результатов.
Предлагается записать домашнее задание:
Прорешать типовые задания ОГЭ (номер 26) с «сайта решу ОГЭ».
Занятие № 5
Тема «Решение типовых задач из ОГЭ по теме Метод площадей»
Тип урока: применения знаний и умений
Цели урока:
-
Рассмотреть типовые задачи из заданий ОГЭ;
-
Понять, как решать типовые задачи из ОГЭ с помощью метода площадей
Программа: «Геометрия. 9 класс»
1. Организационный этап.
Учитель приветствует класс, отмечают отсутствующих на уроке учащихся, проверяется готовность учеников к занятию.
2. Подготовительный этап
Проверка домашнего задания.
Учитель спрашивает желающих, кто готов выйти к доске и решить типовое задание из ОГЭ.
3. Мотивационный этап
После проверки домашнего задания педагог пишет на доске и проговаривает вслух тему урока и кратко подводит учеников к тому, что сегодня будет рассматриваться и как это поможет в будущем.
4. Этап закрепления полученных ранее знаний
Учитель пишет на доске условие задачи и предлагает желающему выйти её решить.
Задача 1. В треугольнике ABC на его медиане BM отмечена точка K так, ч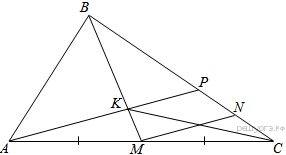 то BK: KM = 10: 9. Прямая AK пересекает сторону BC в точке P. Найдите отношение площади четырёхугольника KPCM к площади треугольника ABС.
то BK: KM = 10: 9. Прямая AK пересекает сторону BC в точке P. Найдите отношение площади четырёхугольника KPCM к площади треугольника ABС.
Рис. 30
Решение:
-
Пусть площадь треугольника ABC равна S. Проведём прямую MN, параллельную AP. Точка M — середина AC, следовательно, MN — средняя линия треугольника APC значит, PN = CN. По теореме Фалеса для угла MBC находим: 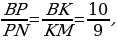 а так как PN = NC, получаем, что
а так как PN = NC, получаем, что 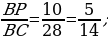
-
Стороны треугольников BKP и BMC сонаправлены, их площади относятся как произведение отношений сонаправленных сторон,
поэтому  ;
;
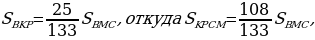
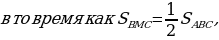
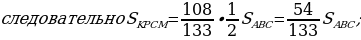
Тем самым, для искомого отношения площадей имеем: 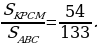
Ответ: 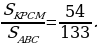
Задача 2. В треугольнике ABC на его медиане BM отмечена точка K так, что BK : KM = 4 : 1. Прямая AK пересекает сторону BC в точке P. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.
Решение:
1. Пусть площадь треугольника ABC равна S. Медиана делит треугольник на два равновеликих треугольника, значит, 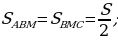
2. У треугольников ABK и ABM высота, проведенная к стороне BM, общая, поэтому площади этих треугольников относятся как их основания BK и BM, откуда: 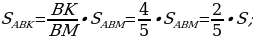
3. Проведём прямую MN, параллельную AP;
4. Точка M — середина AC, следовательно, MN — средняя линия треугольника APC, значит, PN = CN;
5. По теореме Фалеса для угла MBC находим: 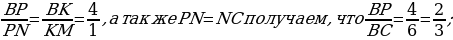
6. Стороны треугольников BKP и BMC сонаправлены, их площади относятся как произведение отношений сонаправленных сторон, поэтому
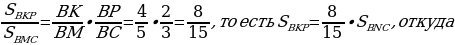

Тем самым, для искомого отношения площадей имеем:
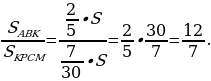
Ответ: 
Задача 3. На сторонах АВ, ВС и АС Δ ABC отмечены точки М, N и К таким образом, что выполняются следующие соотношения:
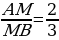
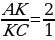
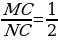
Необходимо рассчитать соотношение, в котором отрезок МК делит отрезок AN (Рис.14)

Рис. 31
Решение:
1.Обозначим в качестве точки пересечения отрезков МК и AN точку P. Далее возьмем к рассмотрению получившийся четырёхугольник AMNK. В соответствии со свойством 3, 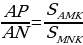 . На основании площади Δ ABC найдем площади Δ AMK и Δ MNK .
. На основании площади Δ ABC найдем площади Δ AMK и Δ MNK .
Таким образом, площадь Δ MNK можно рассчитать на базе следующего соотношения:
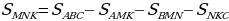 (1).
(1).
В Δ AMK и Δ ABC есть общий угол, поэтому можно отметить:
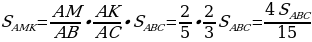
Аналогично находим
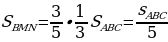
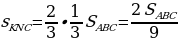
Подставляя в (1), получаем, что
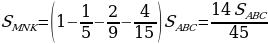
Следовательно,
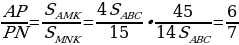
Ответ: 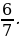
Задача 4. Дана трапеция ABCD, её основания ВС и AD равны 2 и 6 соответственно. Диагонали BD и АС пересекаются в точке О. Точка Р – середина OD. 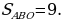 Найдите площадь четырехугольника АВСР. (Рис.15).
Найдите площадь четырехугольника АВСР. (Рис.15).

Рис. 32
Решение:
-
Пусть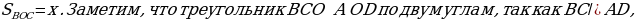 угол ВСА = углу САD как накрест лежащие и угол ВОС = углу AOD как вертикальные. Следовательно,
угол ВСА = углу САD как накрест лежащие и угол ВОС = углу AOD как вертикальные. Следовательно,
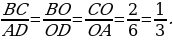
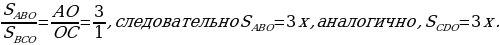
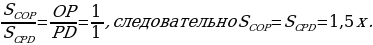
-
Площади подобных треугольников относятся как коэффициент подобия в квадрате, следовательно, 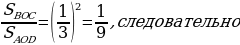
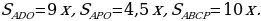 Так как 3х = 9, то х = 3 и, следовательно,
Так как 3х = 9, то х = 3 и, следовательно, 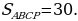
Ответ:30.
5. Подведение итогов. Рефлексия. Домашнее задание.
Обсуждение с обучающимися результатов занятия, оценка ими новизны и полезности полученной информации, оценка доступности и качества усвоения новых знаний и умений, самооценка своих результатов.
Предлагается записать домашнее задание:
Подготовиться к контрольной работе.
Итоговая контрольная работа
по теме «Метод площадей»
Пояснительная записка
Данную контрольную работу рекомендуется давать учащимся 9 классов после изучения темы «Метод площадей».
Контрольная работа включает в себя задачу, требованием которой является:
-
Умение применять свойства площадей для решения задач. Основные знания и умения, проверяемые в ходе контрольной работы:
Знания:
Умения:
-
применять свойства площадей;
-
анализировать условие задачи;
-
выстраивать логическую цепочку рассуждений.
| Контрольная работа по теме: «Метод площадей» I вариант Задание 1: Запиши 1 свойство площадей (формулировка, чертеж, доказательство). Задание 2: Запиши 4 свойство площадей (формулировка, чертеж, доказательство). Задание 3: Реши задачу: Дана трапеция ABCD, её основания ВС и AD равны 2 и 6 соответственно. Диагонали BD и АС пересекаются в точке О. Точка Р – середина OD. 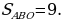 Найдите площадь четырехугольника АВСР. Найдите площадь четырехугольника АВСР.
|
| Контрольная работа по теме: «Метод площадей» II вариант Задание 1: Запиши 2 свойство площадей (формулировка, чертеж, доказательство). Задание 2: Запиши 6 свойство площадей (формулировка, чертеж, доказательство). Задание 3: Внутри равностороннего треугольника со стороной m движется точки. Докажите, что сумма расстояний от этой токи до сторон треугольника не меняется, и найдите эту сумму. |
Описание пооперационного состава действий заданий контрольной работы
| № задания | Операции |
| 1. | 1) Написать формулировку данного свойства |
| 2) Построить чертеж |
| 3) Расписать доказательство данного свойства |
| 2. | 1) Написать формулировку данного свойства |
| 2) Построить чертеж |
| 3) Расписать доказательство данного свойства |
| 3. | 1) Построить чертеж |
| 2) Расписать подробное решение с обоснованием |
Баллы по каждому задания:
1 задание – 3 балла;
2 задание – 3 балла;
3 задание – 2 балла.
Критерии оценивания работы:
Для получения отметки «5» необходимо набрать 8 баллов;
Для получения отметки «4» необходимо набрать 6-7 баллов;
Для получения отметки «3» необходимо набрать 4-5 баллов.
Заключение
На сегодняшний момент времени геометрический метод площадей имеет особое значение, так как его применения требует широкий спектр задач из школьного курса геометрии. Если школьник владеет таким методом, то он с легкостью может решать различные задачи, включенные как в 1, так и во 2 часть в ОГЭ по математике.
Элективный курс по математике позволяет создать условия для существенной дифференциации содержания обучения старшеклассников с широкими и гибкими возможностями построения индивидуальных образовательных программ.
В процессе выполнения решены следующие задачи:
- проанализирована учебно-методическая литература по теме исследования;
- описано теоретическое содержание элективного курса по обучению применения метода площадей;
- разработано практическое содержание модуля элективного курса;
- составлены планы практических занятий по основным темам модуля.
Поставленные задачи решены, цель – разработка модуля элективного курса для обучения применению метода площадей к решению задач в 9 классе – достигнута.
СПИСОК ЛИТЕРАТУРЫ
Книга одного автора:
-
Болтянский, В. Г. Элементарная геометрия. Пособие для учителей / В. Г. Болтянский. - М. : Просвещение, 1985. – 320 с.
-
Готман Э. Г. Задачи по планиметрии и методы их решения: Пособие для учащихся / Э. Г. Готман. - М. : Просвещение,1996. – 243 с.
-
Готман Э. Г. Стереометрические задачи и методы их решения / Э. Г. Готман. - М. : МЦНМО, 2006. – 160 c.
-
Погорелов А. В. Геометрия: Учебник для 7-11 классов общеобразовательных учреждений / А. В. Погорелов. – 5-е изд. - М. : Просвещение, 1995. – 383 с.: ил.
Книга двух авторов:
-
Готман Э. Г. Задача одна - решения разные: Геометрические задачи: Книга для учащихся. / Э. Г. Готман, З. А. Скопец. - М. : Просвещение, 2000. - 224 с.
-
Готман Э. Г. Решение геометрических задач аналитическим методом: Пособие для учащихся 9 и 10 классов / Э. Г. Готман, З. А. Скопец - М.: Просвещение, 1979. – 128 с.
-
Смирнов В. А. Геометрия. Задачи на доказательство / А. В. Смирнов, И. М. Смирнова. – М. : Бином, 2015. – 309 с.
Книга трех авторов:
-
Дубровин Б. А. Современная геометрия. Методы и приложения / А. Б. Дубровин, С. П. Новиков, А. Т. Фоменко. - 2-е изд., испр. - М. : Наука, 1986. – 760 с.
Книга четырех и более авторов
-
Геометрия. 10 - 11 классы. Учебник. Базовый и углубленный уровни / Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев [и др.] — 9-е изд. — М. : Просвещение, 2021. — 287 с. : ил.
Статья из периодического издания (журнала, газеты)
-
Ермаков, Д. С. Создание элективных учебных курсов для профильного обучения [Текст] / Д. С. Ермаков, Г. Д. Петрова // Школьные технологии. – 2003. - №6. – С. 22-29.
-
Кузовлев, А. Расположение корней квадратного трехчлена при решении задач с параметрами [Текст] / А. Кузовлев // Математика. – 2004. - №34. – С. 19-27.
-
Смирнов В. А. Построения на клетчатой бумаге [Текст] / В. А. Смирнов, И. М. Смирнова [Текст] // Математика в школе. – 2011. - №5. – С. 17-24.
Электронные ресурсы
-
https://www.elibrary.ru/item.asp?id=37240700
Коваленко, Е. С., Кузуб Н. М. Применение метода объёмов для решения стереометрических задач при подготовке к ЕГЭ по математике: [Электронный ресурс]. (Дата обращения: 06. 11. 2019)
-
https://sibac.info/archive/technic/11
Мельникова М. Р., Квалтырева Е. В., Ганеева А. Р. Использование «Метода объёмов» для решения стереометрических задач [Электронный ресурс] // Научное сообщество студентов XXI столетия. Технические науки: Электронный сборник статей по материалам LXXI студенческой международной научно-практической конференции. - 2018. – №11 (70). – с. 73-80. (Дата обращения: 5. 01. 2022)
-
https://math-ege.sdamgia.ru/prob_catalog
Решу ЕГЭ. Математика профильного уровня. Каталог заданий по типам: [Электронный ресурс]. (Дата обращения: 04. 12. 2019)







 оказательство:
оказательство: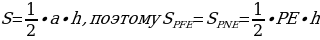 [1,5].
[1,5]. оказательство:
оказательство: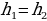 в двух треугольниках (Рис.3) с основаниями a и b. Рассмотрим отношение площадей этих треугольников
в двух треугольниках (Рис.3) с основаниями a и b. Рассмотрим отношение площадей этих треугольников 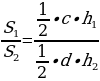
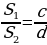 [5].
[5].  оказательство:
оказательство: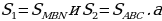
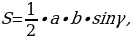 рассмотрим отношение площадей треугольников АВС и MBN.
рассмотрим отношение площадей треугольников АВС и MBN. 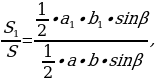 упростив получим
упростив получим 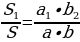 [5].
[5].  оказательство:
оказательство: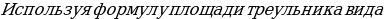
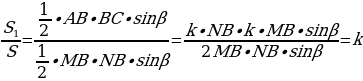 .
. 
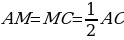 . Медиана делит треугольник на два с одинаковой высотой. Найдем площади треугольников АВМ и МВС по формуле
. Медиана делит треугольник на два с одинаковой высотой. Найдем площади треугольников АВМ и МВС по формуле 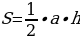 . Получим
. Получим 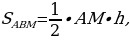
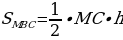 значит
значит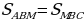 .
.
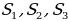 , а площадь треугольника АВС равна S. Рассмотрим треугольники АВК и
, а площадь треугольника АВС равна S. Рассмотрим треугольники АВК и 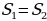 , аналогично доказывается, что
, аналогично доказывается, что 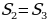 и
и 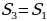 .
.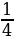 S [5].
S [5].
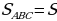 , то
, то 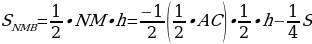 . Аналогично можно доказать, что площади всех треугольников равны одной четвертой части площади треугольника АВС.
. Аналогично можно доказать, что площади всех треугольников равны одной четвертой части площади треугольника АВС.
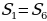 . Аналогично
. Аналогично 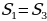 . Если
. Если  и так далее, в результате получим, что все шесть треугольника имеют равные площади и они составляют шестую часть от площади треугольника АВС.
и так далее, в результате получим, что все шесть треугольника имеют равные площади и они составляют шестую часть от площади треугольника АВС.
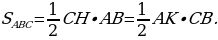
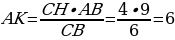
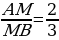
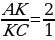
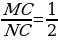

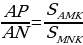 . На основании площади Δ ABC найдем площади Δ AMK и Δ MNK . Таким образом, площадь Δ MNK можно рассчитать на базе следующего соотношения:
. На основании площади Δ ABC найдем площади Δ AMK и Δ MNK . Таким образом, площадь Δ MNK можно рассчитать на базе следующего соотношения: 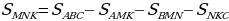 (1).
(1).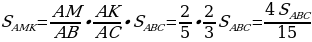
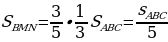
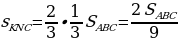
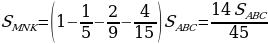
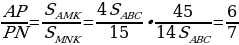
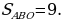 Найдите площадь четырехугольника АВСР.
Найдите площадь четырехугольника АВСР. 
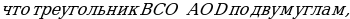
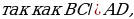
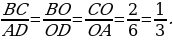
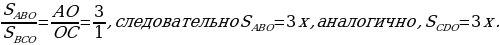
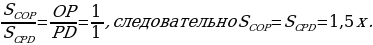
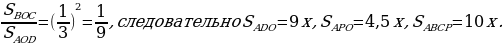 Так как 3х = 9, то х = 3 и, следовательно,
Так как 3х = 9, то х = 3 и, следовательно, 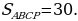

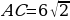 , угол
, угол 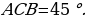
 айти:
айти: 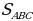
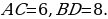
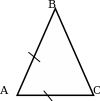 айти:
айти: 
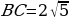 , угол
, угол 

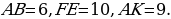

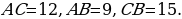
 айти:
айти: 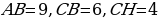 .
.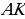
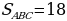 .
.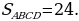
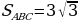 .
.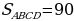 .
.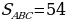 .
.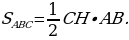

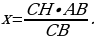
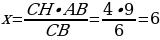

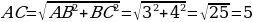
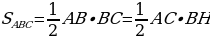 , из данного равенства выделим высоту:
, из данного равенства выделим высоту: 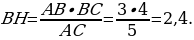

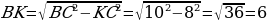
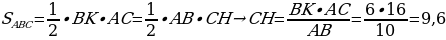


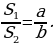

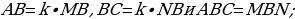
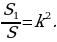
 адача №1: через вершину треугольника ABC проведена прямая m, параллельная стороне АВ. Докажите, что все треугольники с вершинами на прямой m и основанием АВ имеют равные площади.
адача №1: через вершину треугольника ABC проведена прямая m, параллельная стороне АВ. Докажите, что все треугольники с вершинами на прямой m и основанием АВ имеют равные площади.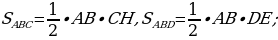
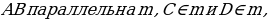
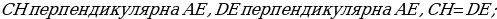
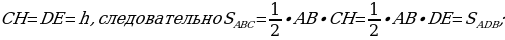
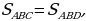 что и требовалось доказать.
что и требовалось доказать.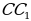 – высота, опущенная на боковую сторону. Докажите, что сумма длин n и m равна высоте
– высота, опущенная на боковую сторону. Докажите, что сумма длин n и m равна высоте 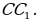

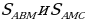 : так как треугольник ABC равнобедренный, то основания у треугольников BAM и MAC – одинаковы, MK – высота первого треугольника, MP – высота второго треугольника. Имеем:
: так как треугольник ABC равнобедренный, то основания у треугольников BAM и MAC – одинаковы, MK – высота первого треугольника, MP – высота второго треугольника. Имеем: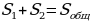
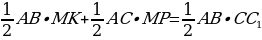
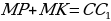





 адача №1: Треугольник АВС разделен медианной МВ на два треугольника. Сравните площади этих треугольников.
адача №1: Треугольник АВС разделен медианной МВ на два треугольника. Сравните площади этих треугольников. 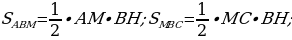
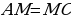 (так как ВМ – медианна)
(так как ВМ – медианна)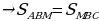 .
.
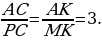
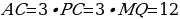
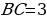 . Тогда
. Тогда 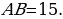
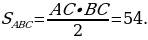
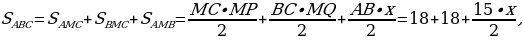 где х – искомое расстояние. Следовательно, х=2,4.
где х – искомое расстояние. Следовательно, х=2,4.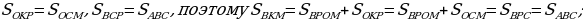
 соответственно. Точка K расположена вне треугольника ABC, причём отрезок KC пересекает сторону AB в точке, отличной от B. Известно, что треугольник с вершинами K, A и C подобен исходному. Найдите косинус угла AKC, если ∠KAC 90°. Найти площадь треугольника АВС.
соответственно. Точка K расположена вне треугольника ABC, причём отрезок KC пересекает сторону AB в точке, отличной от B. Известно, что треугольник с вершинами K, A и C подобен исходному. Найдите косинус угла AKC, если ∠KAC 90°. Найти площадь треугольника АВС.
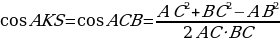 =
= 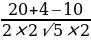 =
= 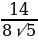 =
= 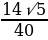 ;
;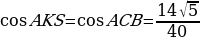 ;
;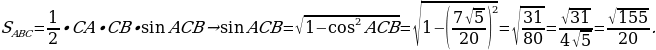
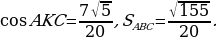
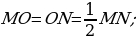
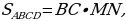 а площадь треугольника
а площадь треугольника 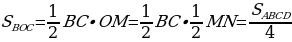 .
. адача 4. Задан треугольник АВС. К стороне СВ проведена высота АК, а к стороне АВ высота СН. Длина АВ составляет 9, СВ – 6, а СН – 4. Найдите длину высоты АК (рис. 13).
адача 4. Задан треугольник АВС. К стороне СВ проведена высота АК, а к стороне АВ высота СН. Длина АВ составляет 9, СВ – 6, а СН – 4. Найдите длину высоты АК (рис. 13). то BK: KM = 10: 9. Прямая AK пересекает сторону BC в точке P. Найдите отношение площади четырёхугольника KPCM к площади треугольника ABС.
то BK: KM = 10: 9. Прямая AK пересекает сторону BC в точке P. Найдите отношение площади четырёхугольника KPCM к площади треугольника ABС.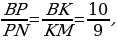 а так как PN = NC, получаем, что
а так как PN = NC, получаем, что 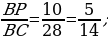
 ;
;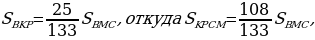
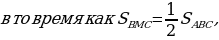
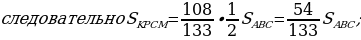
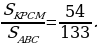
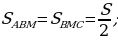
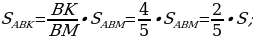
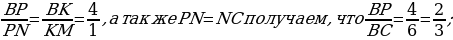
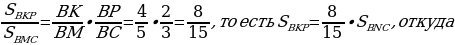

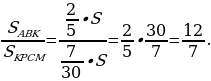


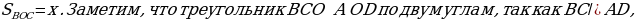 угол ВСА = углу САD как накрест лежащие и угол ВОС = углу AOD как вертикальные. Следовательно,
угол ВСА = углу САD как накрест лежащие и угол ВОС = углу AOD как вертикальные. Следовательно,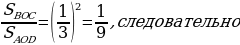
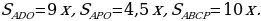 Так как 3х = 9, то х = 3 и, следовательно,
Так как 3х = 9, то х = 3 и, следовательно, 
















