Оглавление
Введение 2
Критерии оценивания 16 задания ЕГЭ 2021 2
Общие рекомендации решения задачи: 3
Теория, которая пригодится при решении 16 задачи ЕГЭ: 4
Простые задачи на отработку теории: 11
Разбор решения задач 12
Задачи на самостоятельное решение: 18
Введение
В данном методическом пособии рассматривается планиметрическая задача ЕГЭ №16. Собранная информация поможет ученикам подготовиться к сдаче экзамена.
Набрать 3 балла за эту задачу получается не у всех учеников, но, на самом деле, она не будет казаться сложной, если правильно подготовиться. Прежде чем приступать к решению таких заданий, следует выучить необходимую теорию. Следующим важным шагом будет решение более простых задач: так вы закрепите теорию на практике, что поможет «видеть» её, и с большей вероятностью запомните. Пример таких задач вы можете найти в этом сборнике. Последний шаг: самостоятельное решение задач с использованием собранной информации. Не останавливайтесь, если у вас не сразу получается: на это нужно время. Вы обязательно справитесь!
Критерии оценивания 16 задания ЕГЭ 2021
| 3 балла | Имеется правильное доказательство утверждения пункта "а", и аргументированно получен правильный ответ в пункте "б" |
| 2 балла | Получен правильный ответ в пункте "б", либо имеется верное доказательство утверждения пункта "а", и при аргументированном решении пункта "б" получен неправильный ответ из-за арифметической ошибки |
| 1 балл | Имеется верное доказательство утверждения пункта "а", либо при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки, либо обоснованно получен верный ответ в пункте "б" с использованием утверждения пункта "а", при этом пункт "а" не выполнен |
| 0 баллов | Решение не соответствует ни одному из критериев, приведённых выше |
Общие рекомендации решения задачи:
-
Внимательно прочитать условие задачи
-
Построить правильный крупный рисунок со всеми обозначениями и пометками. Этот этап очень важен, так как визуальное восприятие повлияет на всё решение задачи
-
При обдумывании задания задавайте себе вспомогательные вопросы:
Зачем нам это дано? Как правило, все данные в задачи используются. Если не получается прийти к решению, то проверьте, всё ли было задействованы.
Что можно найти из дано?
Каким образом я могу получить/ доказать / прийти к выводу что…?
Что я знаю про…(радиус окружности)?
Эти вопросы помогут вам прийти к решению
-
После доказательства пункта а) перейти к пункту б), но важно помнить, что пункт а) обычно используется при решении пункта б).
-
Смотреть №3
-
После решения задачи нужно проверить на наличие арифметических и логических ошибок, всё ли записано правильно и т. д.
Теория, которая пригодится при решении 16 задачи ЕГЭ:
Четырёхугольники:
-
Четырехугольник можно вписать в окружность тогда и только тогда, когда сумма его противоположных углов равна 180 градусов

-
В четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противоположных сторон равны

-
Если окружность вписана в равнобедренную трапецию, то боковая сторона трапеции равна ее средней линии

-
Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований

-
Точка пересечения диагоналей трапеции, точка пересечения продолжений ее боковых сторон и середины оснований лежат на одной линии

-
Площадь выпуклого четырехугольника равна половине произведения диагоналей на синус угла между ними

Треугольники:
-
Медиана, проведённая к гипотенузе прямоугольного треугольника, является радиусом описанной окружности
-
Медиана, проведённая из вершины прямого угла к гипотенузе, равна половине гипотенузы
 CO=BO=AO=R
CO=BO=AO=R
-
Высота, проведенная из вершины прямого угла, равна среднему геометрическому проекций катетов на гипотенузу

-
Отношение площадей подобных треугольников равно квадрату коэффициента подобия
-
Теорема Пифагора: сумма квадратов длин катетов равна квадрату длины гипотенузы
-
Обратная теорема Пифагора: если в треугольнике квадрат одной стороны равен сумме квадратов двух других сторон, то треугольник прямоугольный
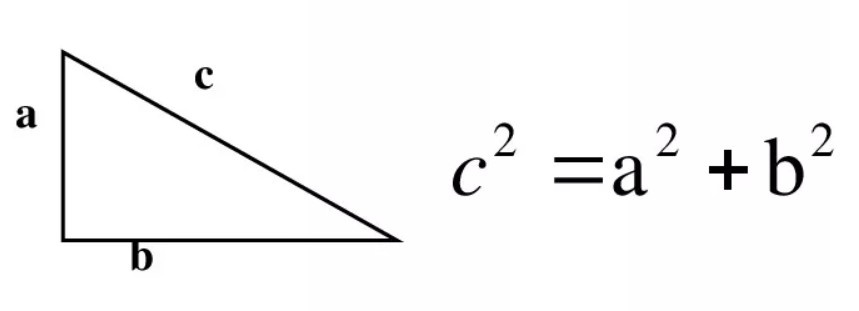
-
Биссектриса угла треугольника делит противолежащую сторону в отношении длин прилежащих сторон

-
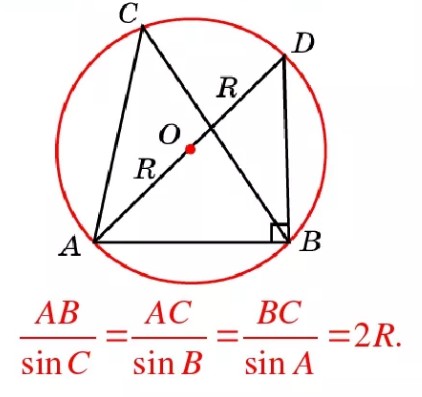
Теорема синусов: стороны треугольника пропорциональны синусам противолежащих углов и это отношение равно удвоенному радиусу описанной около треугольника окружности
-
Теорема косинусов: квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними

-
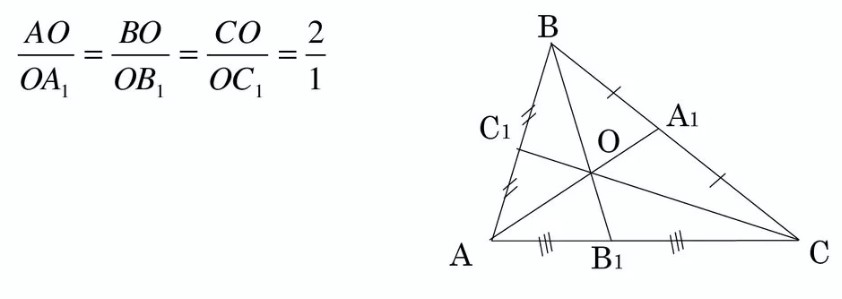
Три медианы треугольника пересекаются в одной точке и делятся в ней в отношении 2:1, считая от вершины
-
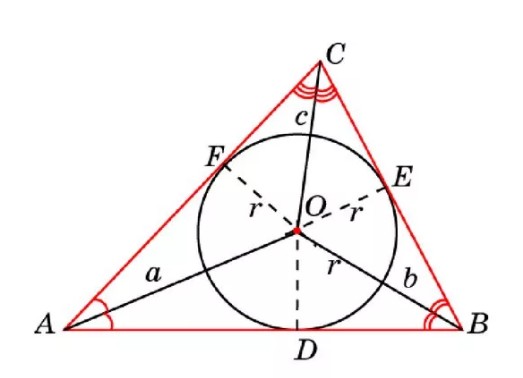
Три биссектрисы треугольника пересекаются в одной точке, являющейся центром окружности, вписанной в треугольник
Касательные и секущие:
-
Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности

-
Если прямая, проходящая через точку, лежащую на окружности, перпендикулярна радиусу, проведенному в эту точку, то она является касательной к окружности
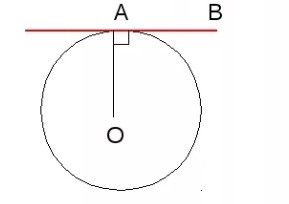
-
Если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть

CM2 = AM*BM
-
Если из точки, лежащей вне окружности, проведены две секущие, то произведение одной секущей на ее внешнюю часть равно произведению другой секущей на её внешнюю часть
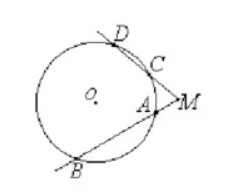
-
Прямая, проходящая через точки пересечения двух окружностей, делит пополам общую касательную к ним
 CN=ND
CN=ND
Окружности:
-
Радиус окружности, проведенный в точку касания, перпендикулярен касательной

-
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды

-
Диаметр, перпендикулярный хорде, делит ее пополам

-
Серединный перпендикуляр к хорде проходит через центр окружности

-
Равные хорды удалены от центра окружности на равные расстояния

-
Линия центров касающихся окружностей проходит через точку касания

-
Центр окружности, вписанной в угол, лежит на биссектрисе этого угла

-
Дуги окружности, заключенные между параллельными хордами, равны

-
Радиус вневписанной окружности, касающейся данной стороны треугольника, равен отношению площади треугольника к разности полупериметра и этой стороны
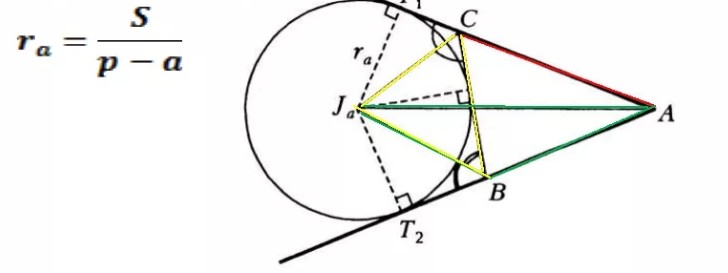
Простые задачи на отработку теории:
-
В треугольнике ABC угол ACB равен 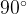 , угол B равен
, угол B равен  , CD — медиана. Найдите угол ACD. Ответ дайте в градусах.
, CD — медиана. Найдите угол ACD. Ответ дайте в градусах.
-
Внутри круга радиуса 15 взята точка М на расстоянии 13 от центра. Через точку М проведена хорда длиной 18. Найдите длины отрезков, на которые точка М делит хорду.
-
Две прямые, проходящие через точку M, лежащую вне окружности с центром O, касаются окружности в точках A и B. Отрезок OM делится окружностью пополам. В каком отношении отрезок OM делится прямой AB?
-
Из одной точки проведены к окружности две касательные длиной 12, а расстояние между точками касания 14,4. Определите радиус окружности.
-
Две окружности радиуса r касаются друг друга. Кроме того, каждая из них касается извне третьей окружности радиуса R в точках A и B соответственно. Найдите радиус r, если AB = 12, R = 8.
-
Диагонали вписанного четырёхугольника ABCD пересекаются в точке K. Известно, что AB = 2, BK = 4, AK = 1, CD = 3. Найдите AC.
-
Две пересекающиеся окружности имеют общую касательную. Расстояние между точками касания равно 4. Расстояние между центрами окружностей равно 5, а радиус меньшей окружности равен 2. Найдите величину радиуса большей окружности.
-
Две окружности касаются друг друга внутренним образом. Известно,
что два радиуса большей окружности, угол между которыми равен 60, касаются меньшей окружности. Найдите отношение радиусов окружностей.
-
Из точки P, расположенной внутри острого угла с вершиной A, опущены перпендикуляры PC и PB на стороны угла. Известно, что ∠CBP = 25. Найдите угол CAP.
-
Дан треугольник со сторонами 10, 24 и 26. Две меньшие стороны являются касательными к окружности, центр которой лежит на большей стороне. Найдите радиус окружности.
Ответы:
-
32; 2) 4 и 14; 3) 1:3; 4) 9; 5) 24; 6) 7; 7) 5; 8) 3:1; 9) 25; 10) 120/17
Разбор решения задач
-
Две непересекающиеся окружности
Прямые, содержащие катеты AC и CB прямоугольного треугольника АСВ, являются общими внутренними касательными к окружностям радиусов 2 и 4. Прямая, содержащая гипотенузу АВ, является их общей внешней касательной.
а) Докажите, что длина отрезка внутренней касательной, проведенной из вершины острого угла треугольника до одной из окружностей, равна половине периметра треугольника АСВ.
б) Найдите площадь треугольника АСВ.
Решение:
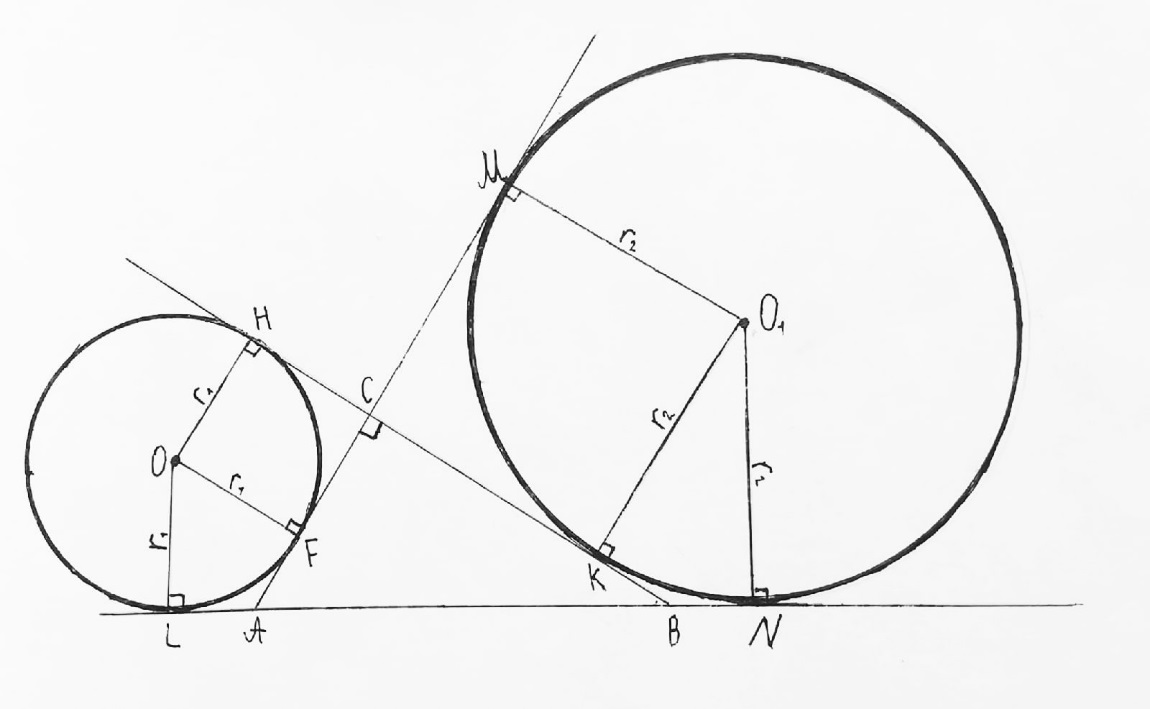
а) 1. H, F, L – точки касания первой окружности, О – её центр;
OL = OH = OF = r1 = 2;
M, K, N - точки касания второй окружности, О1 – её центр;
O1M = O1K = O1N = r2 = 4
2. Отрезки касательных к окружности равны, значит AM=AN, CM=CK, KB=BN, BH=BL, CA=CH, AL=AF
3. Распишем периметр ABC:
Р = AC+AB+CB = AC+AB+CM+BN = AM+AN т. к. AN=AM то P=2AM;
AM=1/2PABC что и требовалось доказать.
б) 1. r1= , где p – полупериметр ABC
, где p – полупериметр ABC
SABC=r1(p-AC) = r1(AM-AC) = r1*CM
2. CM=r2 т. к. CMO1K – квадрат ( ∠CMO1=∠CKO1=∠MCK=90°,значит, CMO1K – прямоугольник, но так как MO1=O1N то это квадрат)
Значит, SABC=r1*r2=2*4=8
Ответ: 8
При решении задач этого типа может понадобиться:
-
Дополнительные построения: Провести линию, соединяющую центры окружностей, и радиусы в точки касания
-
Теория: Свойство касательных и секущих,
-
Центр окружности, вписанной в угол
-
Формула радиуса вневписанной окружности
-
Две окружности, касающиеся внешним образом
Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.
а) Докажите, что прямые AD и BC параллельны.
б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.
Решение:

а) 1. Пусть общая касательная, проведённая к окружностям в точке K пересекает AB в точке N.
Тогда по свойству касательных, проведённых из одной точки, AN=KN=NB.
2. AKB: KN=1/2AB, KN – медиана, значит, треугольник AKB прямоугольный, ∠AKB=90°;
∠AKD=90° - вписанный, значит, опирается на диаметр AD;
O1A⊥AB как радиус проведённый в точку касания.
3. ∠BKC=90° - вписанный, значит, опирается на диаметр BC;
O2B⊥AB как радиус проведённый в точку касания.
4/ AD⊥AB, BC⊥AB, значит AD∥BC что и требовалось доказать.
б) 1. R1=O1A=O1D=4, R2=O2C=O2B=1
2. Треугольники BKC и AKD подобны, 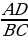 =
= =4
=4
Пусть SBKC=S, тогда SAKD=16S
3. У треугольников AKD и AKB общая высота, следовательно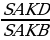 =
=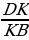 =
=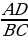 , то есть SAKB = 4S; Аналогично, SCKD = 4S
, то есть SAKB = 4S; Аналогично, SCKD = 4S
4. Площадь трапеции ABCD=16S+4S+4S+S=25S
5. Проведём к AD перпендикуляр O2H, равный высоте трапеции;
O1H=O1A-O2B
O2H= √O1O22-O1H2 = 4
6/ SABCD= 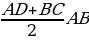 =20
=20
Следовательно, 25S = 20, откуда S = 0,8 и SAKB = 4S = 3,2.
Ответ: 3,2
При решении задач этого типа может понадобиться:
-
Дополнительные построения: Провести линию, соединяющую центры окружностей, опустить высоту из центра одной окружности на радиус другой
-
Вписанные, центральные углы
-
Теория: свойства касательных и секущих
-
-
Две окружности, касающиеся внутренним образом
Две окружности касаются внутренним образом в точке A, причём меньшая проходит через центр большей. Хорда BC большей окружности касается меньшей в точке P. Хорды AB и AC пересекают меньшую окружность в точках K и M соответственно.
а) Докажите, что прямые KM и BC параллельны.
б) пусть L — точка пересечения отрезков KM и AP. Найдите AL, если радиус большей окружности равен 10, а BC = 16.
Решение:

а) 1. Пусть O — центр большей окружности, а O1 - центр меньшей окружности
2. Линия центров касающихся окружностей проходит через точку касания, поэтому OA — диаметр меньшей окружности
3. ∠AKO = 90° так как он центральный, значит, OK⊥AB
4. ABO: OK - высота, OA=OB=R; значит, OK- медиана, AK=KB=1/2AB;
Аналогично, AM=MC=1/2AC
То есть, KM — средняя линия треугольника ABC
Значит, KM∥BC что и требовалось доказать.
б) 1. Опустим перпендикуляр OH на хорду BC, тогда H — середина BC,
2. OHB: OH=6 по теореме Пифагора
3. OH∥O1P;
Опустим перпендикуляр O1E из центра меньшей окружности на OH
OE = OH − EH = OH – O1P = 6 − 5 = 1;
PH2 = O1E2 = O1O2 − OE2 = 25 − 1 =24;
OP2 = OH2 + PH2 = 36 + 24 = 60
4. APO: AP=2 √10 по теореме Пифагора;
5. Отрезок KM — средняя линия треугольника ABC, поэтому L - средина AP
Следовательно, AL=1/2AP=√10
Ответ: √10
При решении задач этого типа может понадобиться:
-
Дополнительные построения: провести линию центров касающихся окружностей, провести перпендикуляр из центра окружности
-
Хорды окружностей
-
Центральные, вписанные углы
-
Две пересекающиеся окружности
Две окружности с центрами O и Q и радиусами 3 и 4 пересекаются в точках A и B. Через точку A проведена прямая MK пересекающая обе окружности в точках M и K, причем точка A находится между ними.
а) Докажите, что треугольники BMK и OAQ подобны.
б) Найдите расстояние от точки B до прямой MK, если OQ = 5, MK = 7.
Решение:

а) 1. ∠AQB – центральный, ∠MKB –вписанный, они опираются на дугу AB, значит, ∠MKB=1/2∠AQB
OQ – биссектриса ∠AQB, значит, ∠AQO=1/2∠AQB=∠MKB
2. ∠AOB – центральный, ∠BMK –вписанный, они опираются на дугу AB, значит, ∠BMK=1/2∠AOB
OQ – биссектриса ∠AOB, значит, ∠AOQ=1/2∠AOB=∠BMK
3. ∠AOQ=∠BMK, ∠AQO=∠MKB, значит треугольники BMK и OAQ подобны по двум углам что и требовалось доказать
б) 1. Заметим, что AO2+AQ2=OQ2 так как 9+16=25
По обратной теореме Пифагора AOQ прямоугольный, ∠OAQ=90°, h – высота в этом треугольнике
2. h= =
=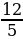
3. BMK~ OAQ, k= =
=
H – высота BMK, H=k*h=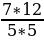 =
=
Ответ: 
При решении задач этого типа может понадобиться:
-
Дополнительные построения: провести линию, соединяющую центры окружностей
-
Подобие треугольников
-
Теорема Пифагора
-
Вписанные, центральные углы
Задачи на самостоятельное решение:
1. Две окружности касаются внутренним образом. Третья окружность касается первых двух и их линии центров.
а) Докажите, что периметр треугольника с вершинами в центрах трёх окружностей равен диаметру наибольшей из этих окружностей.
б) Найдите радиус третьей окружности, если известно, что радиусы первых двух равны 4 и 1
2. Две окружности пересекаются в точках P и Q. Прямая, проходящая через точку P, второй раз пересекает первую окружность в точке A, а вторую — в точке D. Прямая, проходящая через точку Q параллельно AD, второй раз пересекает первую окружность в точке B, а вторую — в точке C.
а) Докажите, что четырёхугольник ABCD — параллелограмм.
б) Найдите отношение CP : PB, если радиус первой окружности втрое больше радиуса второй.
3. К двум непересекающимся окружностям равных радиусов проведены две параллельные общие касательные. Окружности касаются одной из этих прямых в точках A и B. Через точку C, лежащую на отрезке AB, проведены касательные к этим окружностям, пересекающие вторую прямую в точках D и E, причём отрезки CA и CD касаются одной окружности, а отрезки CB и CE — другой.
а) Докажите, что периметр треугольника CDE вдвое больше расстояния между центрами окружностей.
б) Найдите DE, если радиусы окружностей равны 5, расстояние между их центрами равно 18, а AC = 8.
4. Две окружности с центрами O1 и O2 пересекаются в точках A и B, причём точки O1 и O2 лежат по разные стороны от прямой AB. Продолжения диаметра CA первой окружности и хорды CB этой окружности пересекают вторую окружности в точках D и E соответственно.
а) Докажите, что треугольники CBD и O1AO2 подобны.
б) Найдите AD, если ∠DAE=∠BAC, радиус второй окружности втрое больше радиуса первой и AB = 3
5. Две окружности касаются внутренним образом в точке A, причём меньшая окружность проходит через центр O большей. Диаметр BC большей окружности вторично пересекает меньшую окружность в точке M, отличной от A. Лучи AO и AM вторично пересекают большую окружность в точках P и Q соответственно. Точка C лежит на дуге AQ большей окружности, не содержащей точку P.
а) Докажите, что прямые PQ и BC параллельны.
б) Известно, что sin ∠AOC=√15/4. Прямые PC и AQ пересекаются в точке K. Найдите отношение QK : KA.

6. Две окружности касаются внешним образом в точке C. Прямая касается меньшей окружности в точке A, а большей — в точке B, отличной от A. Прямая AC вторично пересекает большую окружность в точке D, прямая BC вторично пересекает меньшую окружность в точке E.
а) Докажите, что прямая AE параллельна прямой BD.
б) Пусть L — отличная от D точка пересечения отрезка DE с большей окружностью. Найдите EL, если радиусы окружностей равны 2 и 5.
7. Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.
а) Докажите, что прямые AD и BC параллельны.
б) Найдите радиус окружности, описанной около треугольника BCD, если известно, что радиус первой окружности равен 4, а радиус второй окружности равен 1.
8. Две окружности пересекаются в точках А и K так, что их центры расположены по разные стороны от прямой, содержащей отрезок АK. Точки В и С лежат на разных окружностях. Прямая, содержащая отрезок АВ, касается одной окружности в точке А. Прямая, содержащая отрезок АС, касается другой окружности также в точке А.
а) Докажите, что углы AKC и AKB равны.
б) Найдите площадь треугольника АВС, если BK = 1, CK = 4, а тангенс угла САВ равен 1/√15.
9. Окружности с центрами O1 и O2 касаются внешним образом в точке C.
К окружностям проведены общая внешняя касательная и общая внутренняя
касательная. Эти касательные пересекаются в точке D.
а) Докажите, что треугольник O1DO2 прямоугольный.
б) Найдите радиусы окружностей, если DO1 =√5 и DO2 =2√5 .
Ответы на часть б):
1) 48/25; 2) 1:3; 3) 12,375; 4) 9; 5) 1:4; 6) 8√19/19; 7) √65; 8) (5+√15)/4; 9) 1 и 4.













 CO=BO=AO=R
CO=BO=AO=R
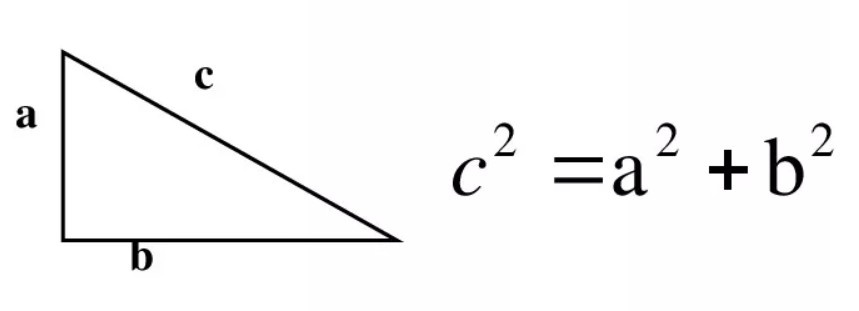









 CN=ND
CN=ND








 , где p – полупериметр ABC
, где p – полупериметр ABC
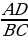 =
= =4
=4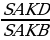 =
=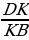 =
=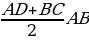 =20
=20

 =
=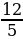
 =
=
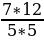 =
=






















