43
Оглавление
Введение……………………………………………………………………………………4
§1. Простейшие тригонометрические уравнения………………………………………..5
§2. Таблица значений тригонометрических функций……………………………………6
§3. Некоторые формулы для обратных тригонометрических функций………………...7
§4. Формулы приведения…………………………………………………………………..8
§5. Знаки тригонометрических функций…………………………………………………9
§6. Четность и нечетность тригонометрических функций……………………………..10
§7. Основные формулы тригонометрии…………………………………………………10
§8. Примеры решения тригонометрических уравнений………………………………..12
§9. Основные способы решения тригонометрических уравнений…………………….14
§10. Задания для самостоятельного решения…………………………………………...26
§11. Отбор корней тригонометрического уравнения…………………………………...31
§12. ПРИЛОЖЕНИЕ (примеры из КИМов ЕГЭ)……………………………………….33
Литература………………………………………………………………………………....37
Введение
Одним из требований к подготовке выпускников указывается готовность использовать приобретенные знания и умения в практической деятельности и повседневной жизни такие как: описание и исследование с помощью функций реальных зависимостей, представление их графически; интерпретация графиков, диаграмм. Огромными возможностями для исследования, применения нестандартных методов решения задач обладают тригонометрические уравнения, для решения которых необходимы систематизированные знания как всех типов уравнений, их методов решения, так и свойств функций, их применение при решении задач.
В настоящее время на первый план выходит задача интеллектуального развития личности, т.е. развитие учебно-познавательной деятельности. И у математики хорошие возможности для реализации данной задачи.
Уже несколько десятилетий тригонометрия, как отдельная дисциплина школьного курса математики не существует, она плавно растеклась в геометрию, алгебру, и в алгебру и начала анализа.
В школьном математическом образовании с изучением тригонометрических уравнений отводится большое внимание.
Требованием нашего времени является необходимость усиления прикладных направлений в обучении математике. Также следует заметить, что решение тригонометрических уравнений создаёт предпосылки для систематизации знаний учащихся, связанных со всем учебным материалом по тригонометрии (например, свойства тригонометрических функций, приёмы преобразования тригонометрических выражений и т.д.) и даёт возможность установить действенные связи с изученным материалом по алгебре (уравнения, равносильность уравнений, неравенства, тождественные преобразования алгебраических выражений и т.д.). Иначе говоря, рассмотрение приёмов решения тригонометрических уравнений предполагает своего рода перенос этих умений на новое содержание.
Практическая значимость пособия заключается в том, разобранные задачи могут активно использоваться учителем в процессе обучения решению тригонометрических уравнений и отбору корней, а репетитору данная работа поможет подготовить выпускника для сдачи ЕГЭ.
§1. Простейшие тригонометрические уравнения.
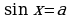
Если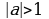
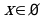 (т.е. решений нет).
(т.е. решений нет).
При 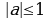 решения находятся по формуле
решения находятся по формуле
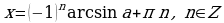 ( Напомним, что
( Напомним, что 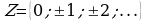 ).
).
Частные случаи:

а) 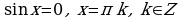

б) 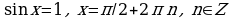

в) 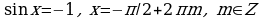
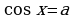
Если 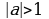
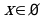
При 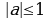 решения находятся по формуле
решения находятся по формуле
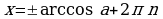 ,
, 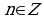
Частные случаи:

а) 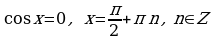

б) 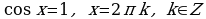

в) 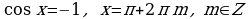
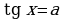 , для любого
, для любого 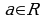
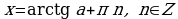
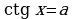 , для любого
, для любого 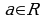
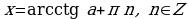
§2. Таблица значений тригонометрических функций.
| 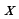
| 0 | 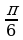
| 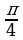
| 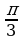
| 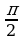
| 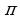
| 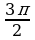
|
| 00 | 300 | 450 | 600 | 900 | 1800 | 2700 |
| 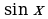
| 0 | 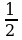
| 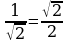
| 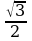
| 1 | 0 | -1 |
| 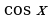
| 1 | 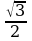
| 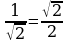
| 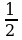
| 0 | -1 | 0 |
| 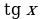
| 0 | 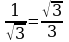
| 1 | 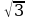
| - | 0 | - |
| 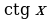
| - | 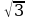
| 1 | 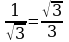
| 0 | - | 0 |
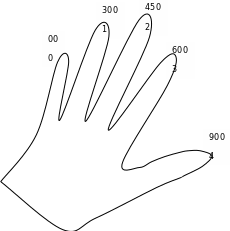
Замечание1. Учащиеся зачастую плохо запоминают таблицу значений тригонометрических функций. Для запоминания значений функций 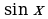 от 00 , 300, 450, 600, 900 можно воспользоваться следующим мнемоническим правилом: пусть
от 00 , 300, 450, 600, 900 можно воспользоваться следующим мнемоническим правилом: пусть 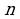 =0, 1, 2, 3, 4 – номера пальцев любой руки, а
=0, 1, 2, 3, 4 – номера пальцев любой руки, а 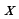 =00, 300, 450, 600, 900 – соответствующие по возрастающему порядку значения углов:
=00, 300, 450, 600, 900 – соответствующие по возрастающему порядку значения углов:
Тогда подставляя в формулу 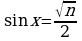 соответствующие значения
соответствующие значения 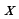 и
и 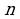 , получим:
, получим:
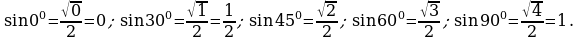
Для определения значений 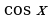 нужно подставлять в формулу
нужно подставлять в формулу 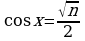 , соответственно,
, соответственно, 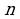 =4 при
=4 при 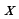 =00,
=00, 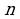 =3 при
=3 при 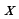 =300,
=300, 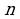 =2 при
=2 при 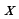 =450,
=450, 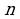 =1 при
=1 при 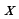 =600,
=600, 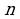 =0 при
=0 при 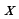 =900, т.е. нумерацию пальцев от 0 до 4 начать с большого пальца (для нашего рисунка).
=900, т.е. нумерацию пальцев от 0 до 4 начать с большого пальца (для нашего рисунка).
Значения 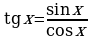 и
и 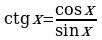 легко определяются по значениям
легко определяются по значениям 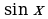 и
и 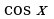 .
.
§3. Некоторые формулы для обратных тригонометрических функций.
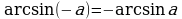 ,
, 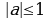 .
.
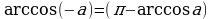 ,
, 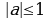 .
.
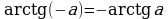 .
.
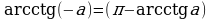 .
.
С помощью этих формул легко определяются значения обратных тригонометрических функций для отрицательного значения аргумента. Например,
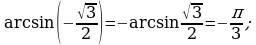
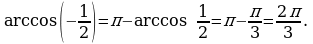
§4. Формулы приведения.
Формулами приведения называются формулы, связывающие тригонометрические функции углов 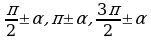 и
и 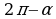 с тригонометрическими функциями угла
с тригонометрическими функциями угла 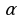 .
.
При применении формул приведения следует ориентироваться на следующее
Правило 10. Если в формуле приведения угол откладывается от вертикального диаметра (т.е. 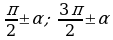 ), то наименование функции меняется на кофункцию (
), то наименование функции меняется на кофункцию (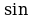 на
на 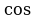 ,
, 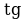 на
на 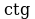 и т.д.);
и т.д.);
Если угол 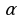 откладывается от горизонтального диаметра (т.е.
откладывается от горизонтального диаметра (т.е.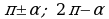 ), то наименование функции не меняется.
), то наименование функции не меняется.
20. Знак преобразованной по формуле приведения правой части определяется по знаку левой части.
Замечание 2. При применении указанного правила угол 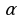 считается острым.
считается острым.
Примеры.
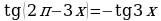
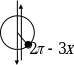 Наименование функции не изменилось, т.к. угол 3
Наименование функции не изменилось, т.к. угол 3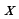
откладывается от горизонтального диаметра. Знак в правой
части равенства взяли с минусом, т.к. угол 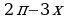 находится
находится
в четвертой четверти, где тангенс отрицателен.
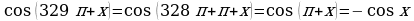
З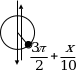 десь мы воспользовались, кроме формулы приведения, еще тем, что функция
десь мы воспользовались, кроме формулы приведения, еще тем, что функция 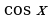 является
является 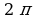 - периодической.
- периодической.
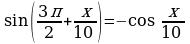
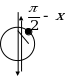
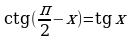
Замечание 3. Применение формул приведения освобождает нас от необходимости запоминания более расширенных таблиц значений тригонометрических функций, приведенных в некоторых учебниках и пособиях.
§5. Знаки тригонометрических функций.
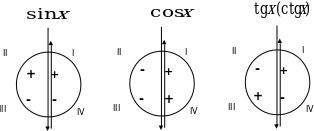
§6. Четность и нечетность тригонометрических функций.
По определению функция 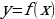 называется четной, если
называется четной, если 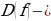 симметричное множество и
симметричное множество и 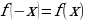 и нечетной, если
и нечетной, если 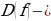 симметричное множество и
симметричное множество и 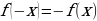 . У тригонометрических функций
. У тригонометрических функций 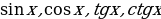 области определения симметричны, кроме того
области определения симметричны, кроме того 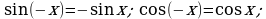
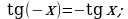
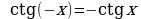 , поэтому
, поэтому 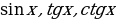 являются нечетными функциями, а
являются нечетными функциями, а 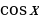 – четной функцией.
– четной функцией.
§7. Основные формулы тригонометрии.
Замечание 4. Доказательство формул 26 - 30 приводится не во всех учебниках и учебных пособиях. Докажем некоторые из них (доказательство остальных приводится аналогично).
Исходя из формулы 6., имеем:
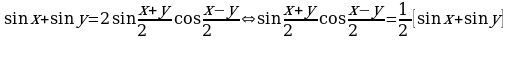
Положим 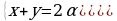 откуда
откуда 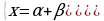 .
.
Тогда последняя формула примет вид
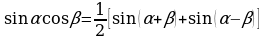 , т.е. формула 27 доказана.
, т.е. формула 27 доказана.
Аналогично доказываются формулы 26. и 28.
Приведем доказательство формулы 29:
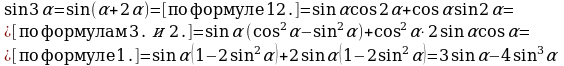
Аналогично доказывается формула 30.
§8. Примеры решения тригонометрических уравнений.
Пример1. Решите уравнение: 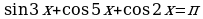
Решение. Т.к.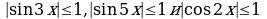 , то левая часть уравнения не может принимать значений больших, чем 3, а правая часть (
, то левая часть уравнения не может принимать значений больших, чем 3, а правая часть (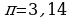 ...) больше 3. Поэтому данное уравнение не имеет корней.
...) больше 3. Поэтому данное уравнение не имеет корней.
Пример 2. Решите уравнение: 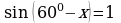
Решение. Мы не можем непосредственно воспользоваться решением уравнения 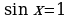 , т.к. недопустимо писать
, т.к. недопустимо писать 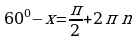 . Здесь возможны два варианта записи решения:
. Здесь возможны два варианта записи решения:
I вариант.
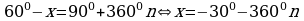 и поскольку
и поскольку 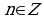 , то полученный результат можно представить в виде:
, то полученный результат можно представить в виде: 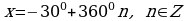 .
.
II вариант.
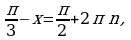
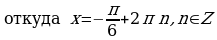 .
.
Замечание 5. Учитывая, что 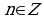 , мы смогли записать решение
, мы смогли записать решение 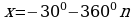 в виде
в виде 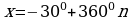 . Этих рассуждений можно было избежать, если бы мы воспользовались нечетностью синуса и запись решения осуществили бы в следующем виде:
. Этих рассуждений можно было избежать, если бы мы воспользовались нечетностью синуса и запись решения осуществили бы в следующем виде: 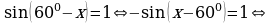
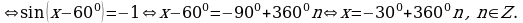
Такая запись решения полезна еще и потому, что при переходе от “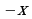 ”к “
”к “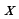 ” возможна ошибка при изменении знаков.
” возможна ошибка при изменении знаков.
Пример 3. Решите уравнение 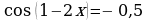 .
.
Решение. С учетом предыдущего замечания решение запишется в виде:
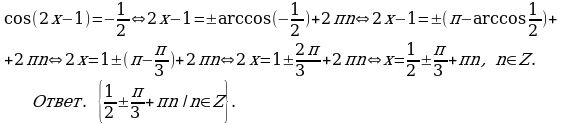
Пример 4. Решите уравнение 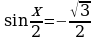
Решение.
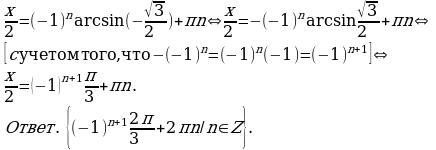
Пример 5. Решите уравнение 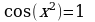 .
.
Решение. 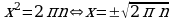
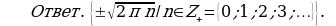
Замечание 6. Этот пример полезен тем, что учащиеся не всегда обращают внимание на наличие “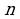 ” под знаком арифметического квадратного корня и пишут
” под знаком арифметического квадратного корня и пишут 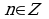 .
.
Пример 6. Решите уравнение 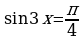 .
.
Решение. 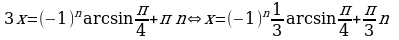
Ответ. 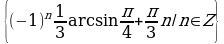 .
.
Замечание 7. При решении такого типа примеров учащимися допускаются следующие ошибки:
1. После записи 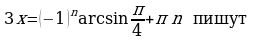
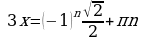
(грубая ошибка из-за неумения пользоваться таблицей значений тригонометрических функций или то же самое - незнание определения обратных тригонометрических функций)
2. После записи
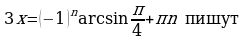
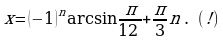 .
.
Пример 7. Решите уравнение: 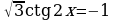 .
.
Решение.
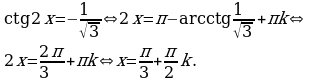
Ответ. 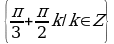 .
.
§9. Основные способы решения тригонометрических уравнений.
I.Уравнения, являющиеся равенством двух одноимённых тригонометрических функций:
а) уравнения вида 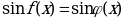 равносильно совокупности уравнений:
равносильно совокупности уравнений:
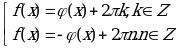
б) уравнения вида 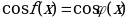 равносильно системе уравнений:
равносильно системе уравнений:
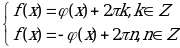
в) уравнения вида 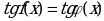 равносильно системе уравнений:
равносильно системе уравнений:
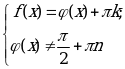
Пример. Решите уравнение: 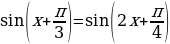 .
.
Решение. Данное уравнение равносильно совокупности:
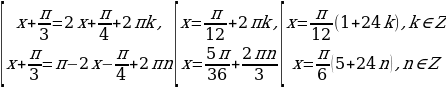
II. Уравнения вида 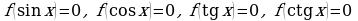 , решаются с помощью соответствующих подстановок
, решаются с помощью соответствующих подстановок
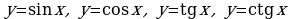 .
.
Например, уравнение 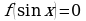 равносильно системе
равносильно системе 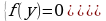
Пример 1. Решите уравнение 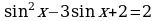 .
.
Решение. Данное уравнение равносильно системе:
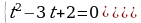 .
.
Ответ.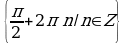 .
.
III. Уравнение вида 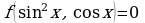 с помощью подстановки
с помощью подстановки 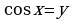 (откуда
(откуда 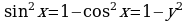 ) приводят к системе:
) приводят к системе:
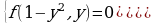
Аналогично уравнения вида 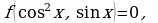
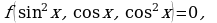
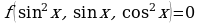 . С помощью соответствующих подстановок
. С помощью соответствующих подстановок 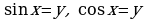 и
и 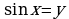 их приводят к системам:
их приводят к системам:
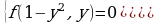 .
.
Пример 2. Решите уравнение 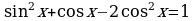 .
.
Решение. Положим 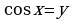 . Тогда получим уравнение
. Тогда получим уравнение
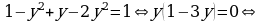
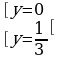 [возвращаясь к первоначальному обозначению]
[возвращаясь к первоначальному обозначению] 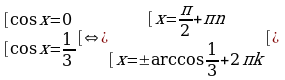 .
.
Ответ.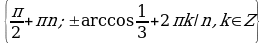 .
.
IV. Однородные тригонометрические уравнения.
Уравнение вида 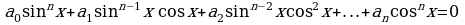 , (1)
, (1)
где 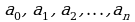 - действительные числа, называется однородным относительно
- действительные числа, называется однородным относительно 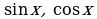 .
.
Если при этом 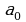 и
и 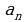 одновременно не равны нулю, то уравнение (1) называется однородным тригонометрическим уравнением
одновременно не равны нулю, то уравнение (1) называется однородным тригонометрическим уравнением 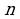 ой степени.
ой степени.
Если 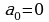 , то корни уравнения
, то корни уравнения 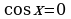 являются решениями уравнения (1).
являются решениями уравнения (1).
Если же 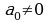 , то
, то 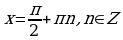 не являются решениями уравнения (1). Действительно, если
не являются решениями уравнения (1). Действительно, если 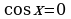 , то из (1) получим, что и
, то из (1) получим, что и 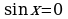 (т.к.
(т.к. 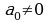 ), что невозможно, т.к. при этом нарушается основное тригонометрическое тождество
), что невозможно, т.к. при этом нарушается основное тригонометрическое тождество 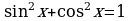 . Поэтому при
. Поэтому при 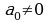 обе части уравнения (1) можно разделить на
обе части уравнения (1) можно разделить на 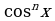 , не нарушая при этом равносильности. Тогда получим уравнение
, не нарушая при этом равносильности. Тогда получим уравнение 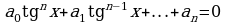 , которое решается подстановкой
, которое решается подстановкой 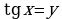 .
.
Пример 3. Решите уравнение 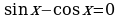 .
.
Решение. Это уравнение является однородным уравнением I степени.
Разделив обе части на 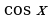 , получим равносильное уравнение
, получим равносильное уравнение 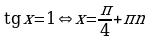
Ответ.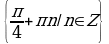 .
.
Пример 4. Решите уравнение 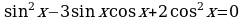 .
.
Решение. Это однородное уравнение второй степени после деления на 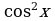 приводится к равносильному
приводится к равносильному
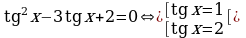
Ответ. 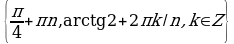 .
.
Пример 5. Решите уравнение 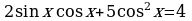 .
.
Решение. По внешнему виду это уравнение не похоже на однородное, т.к. в правой части постоянное число отлично от нуля. Но учитывая, что 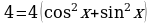 , получим равносильное уравнение
, получим равносильное уравнение 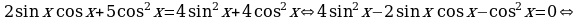
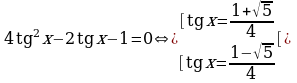 .
.
Ответ.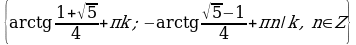 .
.
Замечание 8. Данное уравнение можно было решить непосредственным делением обоих его частей на 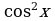 , учитывая, что
, учитывая, что 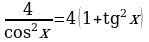 .
.
Замечание 9. Тождество 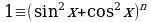 позволяет привести к однородным и следующее уравнение
позволяет привести к однородным и следующее уравнение
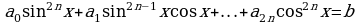 .
.
Пример 6. Решите уравнение 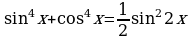 .
.
Решение. Можно преобразовать 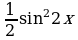 к виду
к виду 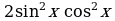 и решить полученное однородное уравнение четвертой степени обычным способом, но мы предложим другой способ:
и решить полученное однородное уравнение четвертой степени обычным способом, но мы предложим другой способ:
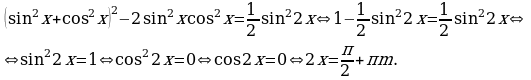
Ответ.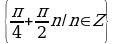 .
.
Пример 7. Решите уравнение 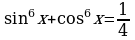 .
.
Решение. Если представить 1/4 в виде 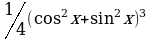 , то получим однородное уравнение 6ой степени. Снова приведем другое решение:
, то получим однородное уравнение 6ой степени. Снова приведем другое решение:
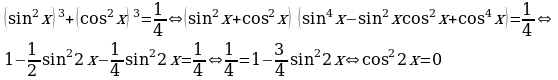 .
.
Ответ. 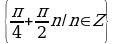 .
.
Пример 8. Решите уравнение 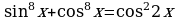 .
.
Решение. Это уравнение также приводится к однородному (докажите!), но пользуясь решением примера 6, можно получить другое решение:
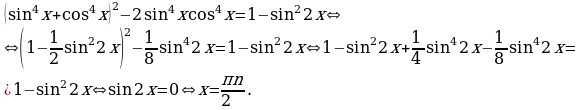
Ответ.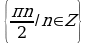 .
.
V. Введение вспомогательного угла.
Этим способом можно решить уравнения вида:
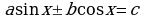 , (2)
, (2)
где 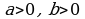 и
и 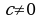 -действительные числа. (Если
-действительные числа. (Если 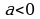 , то умножая обе части уравнения на (-1), приводим его к равносильному виду (2)).
, то умножая обе части уравнения на (-1), приводим его к равносильному виду (2)).
Для решения уравнения (2), разделим обе его части почленно на 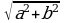 :
:
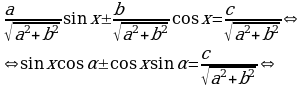
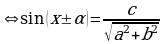 (3)
(3)
где 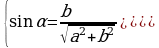 , откуда
, откуда 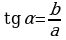
и 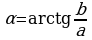 (учитывая, что
(учитывая, что 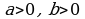 ) (4)
) (4)
Заметим, что т.к.
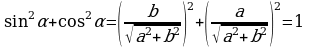 , то угол
, то угол 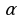 существует.
существует.
Таким образом, уравнение (2) равносильно уравнению (3), где 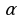 определяется из (4). Решение же уравнения (3) не составляет труда.
определяется из (4). Решение же уравнения (3) не составляет труда.
Замечание. К сожалению, внимание учащихся нечасто обращается на преобразование выражения 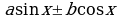 ,.
,.
Пример 9. Решите уравнение: 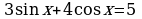 .
.
Решение. 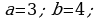
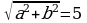 ;
; 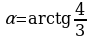 , следовательно, уравнение равносильно следующему:
, следовательно, уравнение равносильно следующему: 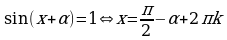 .
.
Ответ. 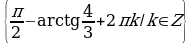 .
.
Пример 10. Решите уравнение 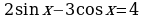 .
.
Решение. Уравнение равносильно следующему:
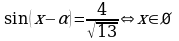 , т.к.
, т.к. 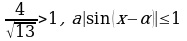 .
.
Ответ. 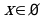 .
.
VI. Замена 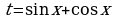 .
.
С помощью такой замены решаются уравнения вида 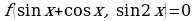 .
.
При этом
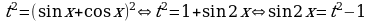
и данное уравнение равносильно системе:
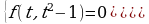 .
.
Пример 11. Решите уравнение: 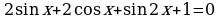 .
.
Решение. Уравнение равносильно системе:
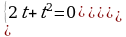
Ответ.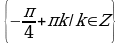 .
.
Замечание10. Уравнения вида 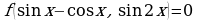 решаются подстановкой
решаются подстановкой 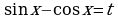 .
.
VII. Метод разложения на множители.
Идею этого метода продемонстрируем на двух примерах.
Пример 12. Решите уравнение: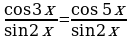 .
.
Решение.
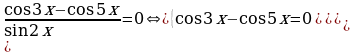 .
.
Ответ.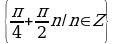 .
.
Иногда, до применения формул сложения следует применить формулы преобразования произведения в сумму.
Пример 13. Решите уравнение: 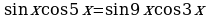 .
.
Решение.
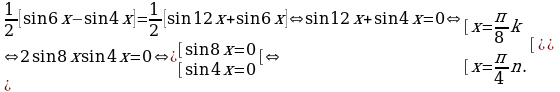
Заметим, что при 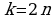 из
из 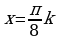 мы получаем
мы получаем 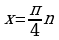 , т.е.
, т.е. 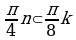 .
.
Ответ. 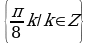 .
.
Замечание11. Способом разложения на множители решаются также уравнения вида: 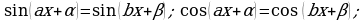
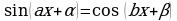 (с учетом того, что
(с учетом того, что 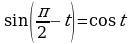 или
или 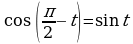 ) и некоторые другие уравнения.
) и некоторые другие уравнения.
VIII. Применение формул 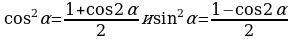
Пример 14. Решите уравнение: 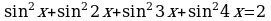 .
.
Решение:
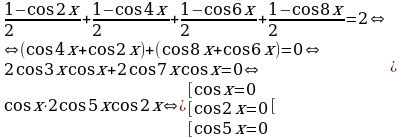
Ответ. 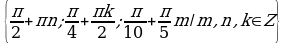 .
.
Замечание12. Этим же способом можно решить уравнения вида
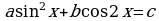 и
и 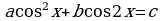 , а также более общее уравнение
, а также более общее уравнение 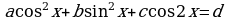 .
.
IX. Универсальная подстановка.
Подстановка 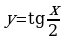 называется универсальной. С ее помощью решаются уравнения вида
называется универсальной. С ее помощью решаются уравнения вида 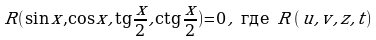 - рациональная функция своих аргументов. При этом
- рациональная функция своих аргументов. При этом 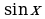 и
и 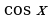 преобразуются по формулам 21 и 22 (см. Основные формулы тригонометрии).
преобразуются по формулам 21 и 22 (см. Основные формулы тригонометрии).
Пример15. Решите уравнение: 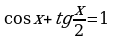 .
.
Решение. Данное уравнение равносильно системе:
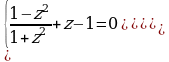 .
.
Ответ. 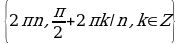 .
.
Замечание13. Формулы 21. и 22. 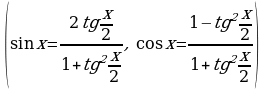 , теряют смысл при
, теряют смысл при 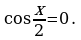 Поэтому при решении уравнений с помощью универсальной подстановки в первую очередь следует проверить, не являются ли значения
Поэтому при решении уравнений с помощью универсальной подстановки в первую очередь следует проверить, не являются ли значения 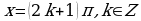 решениями данного уравнения.
решениями данного уравнения.
X. Применение формул приведения.
Пример 16. Решите уравнение 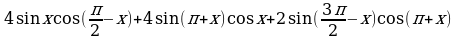
Применяя формулы приведения, преобразуем исходное уравнение к равносильному виду:
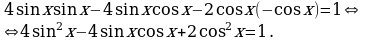
Полученное однородное уравнение второй степени решается обычным способом:
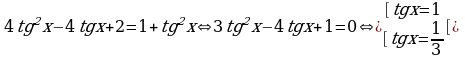
Ответ. 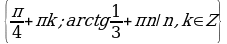 .
.
XI. Оценка левой и правой частей уравнения.
Этим способом мы воспользовались в примерах решения тригонометрических уравнений (Пример 1). Приведем более сложные уравнения.
Пример 17. Решите уравнение.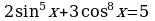 .
.
Решение. Т.к. 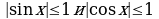 , то
, то
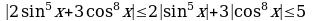 , причем равенство достигается только в том случае, если одновременно
, причем равенство достигается только в том случае, если одновременно 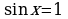 и
и 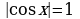 , что невозможно (т.к. нарушается основное тождество
, что невозможно (т.к. нарушается основное тождество 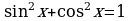 ).
).
Ответ. 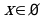 .
.
Пример 18. Докажите, что уравнение 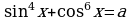 не имеет решения при
не имеет решения при 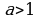 .
.
Решение. Здесь грубые оценки 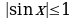 и
и 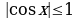 не приведут к цели. Поэтому воспользуемся неравенствами:
не приведут к цели. Поэтому воспользуемся неравенствами: 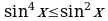 , а
, а 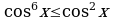 . Складывая почленно правые и левые части последних неравенств, получаем:
. Складывая почленно правые и левые части последних неравенств, получаем: 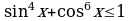 , откуда и следует, что исходное уравнение не имеет решения при
, откуда и следует, что исходное уравнение не имеет решения при 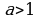 .
.
XII. Применение формул sin3 = 3sin - 4sin3, cos3 = 4cos3 - 3cos.
Пример 19. Решите уравнение: 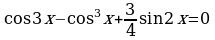 .
.
Решение. 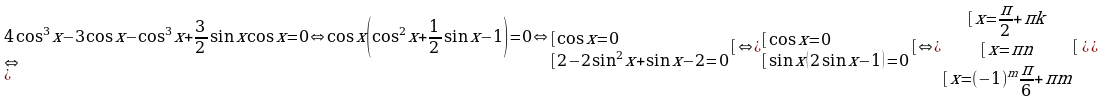 .
.
Ответ. 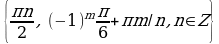 .
.
Пример 20. Решите уравнение: 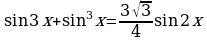 .
.
Решение.
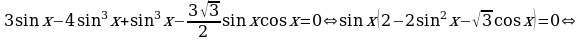
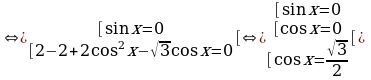 .
.
Ответ. 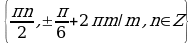 .
.
§10. Задания для самостоятельного решения
Решите уравнения:
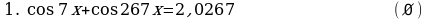
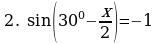
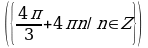
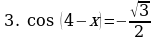
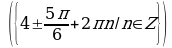
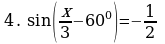
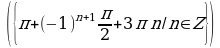
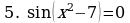
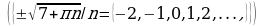
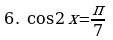
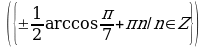
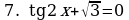
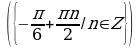
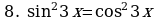
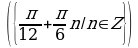
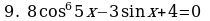
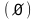
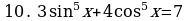
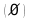
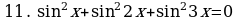
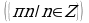
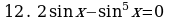
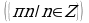
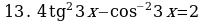
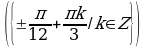
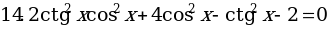
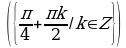
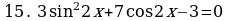
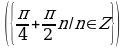
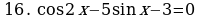
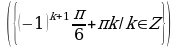
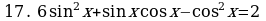
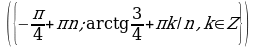
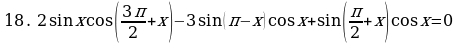
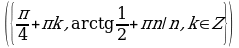
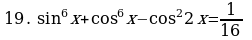
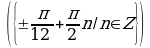
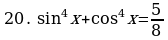
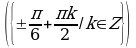
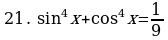
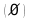
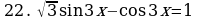
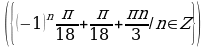
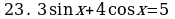
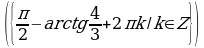
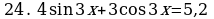
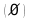
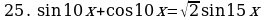
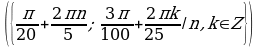
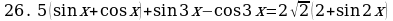
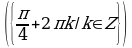
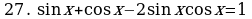
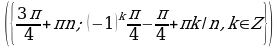
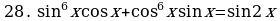
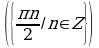
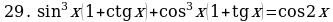
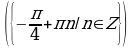
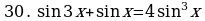
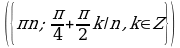
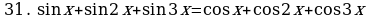
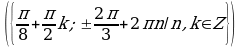
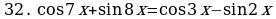
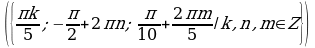
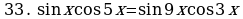
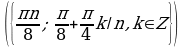
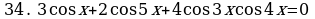
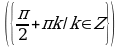
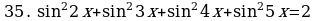
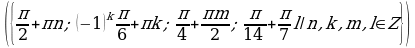
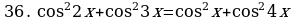
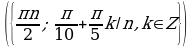
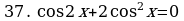
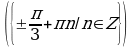
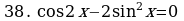
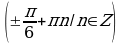
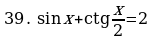
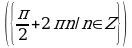
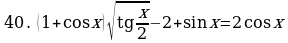
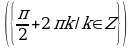
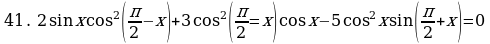
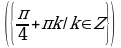
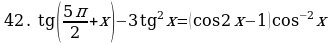
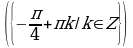
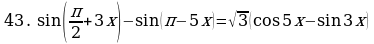
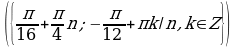
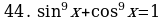
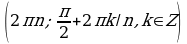
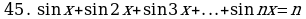
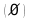
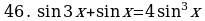
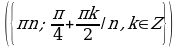
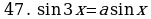
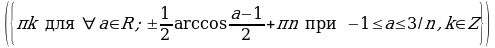
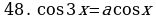
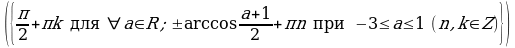
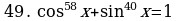
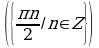
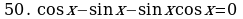
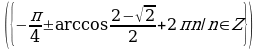
§11. Отбор корней тригонометрического уравнения.
Как выполнить выбор корней с помощью тригонометрического круга? Иногда бывает не просто найти заданный промежуток на тригонометрическом круге. Если вы не понимаете, как работать с помощью тригонометра, то можно делать выбор корней с помощью решения неравенства или с помощью графика.
Способ перевода в градусную меру.
Пример. Решите уравнение 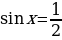 и найдите корни из промежутка
и найдите корни из промежутка
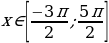 .
.
Решение. х=(-1)k 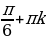 , k
, k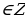 . Это означает, что x=30°+360°∙n или x=150°+360°∙n. Условие
. Это означает, что x=30°+360°∙n или x=150°+360°∙n. Условие 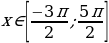 можно записать в виде x∈[-270°;450°]. Указанному промежутку принадлежат следующие значения: 30°, 150°, –210°, 390°. Остается перевести найденные значения в радианы :
можно записать в виде x∈[-270°;450°]. Указанному промежутку принадлежат следующие значения: 30°, 150°, –210°, 390°. Остается перевести найденные значения в радианы : 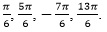
Заметим, что это не самый изящный способ решения подобных заданий, но он может оказаться полезным на первых порах освоения действия, в работе со «слабыми» учениками.
Способ перебора.
Пример. Решите уравнение 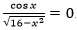 и найдите его корни
и найдите его корни 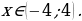
Решение. 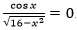
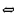
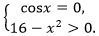
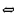
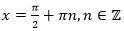
Выполним перебор:
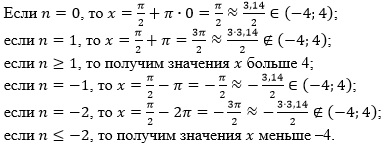
Итак, х 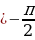 и х
и х 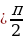
Способ оценки.
Найдите корни уравнения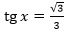 , удовлетворяющие условию
, удовлетворяющие условию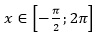 .
.
Решение. Корни уравнения имеют вид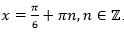 . Потребуем, чтобы выполнялось условие
. Потребуем, чтобы выполнялось условие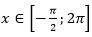 . Решим двойное неравенство:
. Решим двойное неравенство:
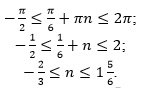
Отсюда n = 0 или n = 1. Значит, 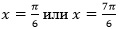 .
.
Графический способ.
Пример. Решите уравнение 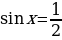 и найдите корни из промежутка
и найдите корни из промежутка
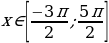 .
.
Решение. Построим график функции y=sinx . Корни данного уравнения являются абсциссами точек пересечения графика с прямой 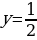 . Отметим такие точки, выделив фрагмент графика на промежутке .
. Отметим такие точки, выделив фрагмент графика на промежутке .
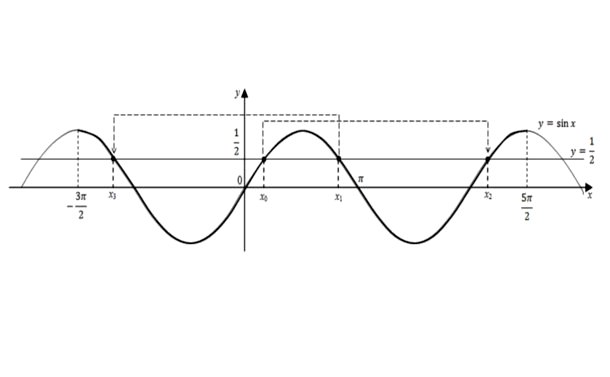
Здесь 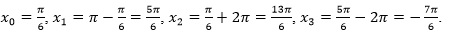
Таким образом, на заданном промежутке уравнение имеет четыре корня: 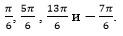
Умение, связанное с поиском решений, удовлетворяющих заданным значениям аргумента, является важным в решении многих прикладных задач. В еще большей степени формированию этого умения способствуют задачи с параметрами и задачи на построение. Необходимо специально формировать умение отбирать корни в процессе изучения всего тригонометрического материала.
В процессе обучения решению задач, в которых требуется отобрать корни тригонометрического уравнения, с учениками следует обсудить разные способы выполнения этого действия, а также выяснить случаи, когда тот или иной способ может оказать наиболее удобным или наоборот непригодным.
§12. ПРИЛОЖЕНИЕ (примеры из КИМов ЕГЭ)
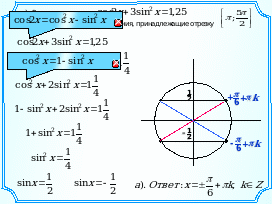
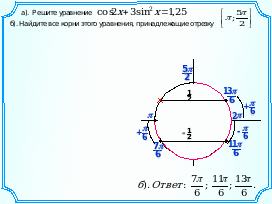
1. а) Решите уравнение cos 2x + 3sin2x = 1,25.
б). Найдите все корни этого уравнения, принадлежащие отрезку .
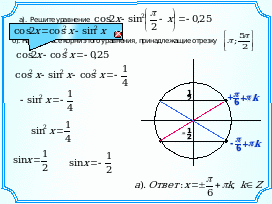
2. а). Решите уравнение cos2x – sin2( – x) = – 0,25.
б). Найдите все корни этого уравнения, принадлежащие отрезку .

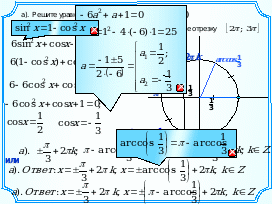
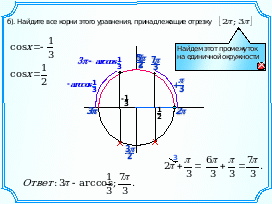
Решите уравнение −6sin2x − cosx + 1 = 0 и найдите корни, принадлежащие промежутку [2; 3].
Литература
Алгебра и начала анализа. 11 класс : учеб. для общеобразовательных учреждений : в 2 ч. Ч. 1. / Г. В. Дорофеев, Е. А. Седова. - М. : Дрофа, 2007. – 334 с.
Алгебра и начала анализа: учеб. для 10-11 кл. общеобразоват. Учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын [и др.]; под ред. А. Н. Колмогорова. – М.: Просвещение, 2008. – 384 с.
Алгебра и начала анализа: учеб. для 11 кл. общеобразоват. учреждений / С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин – М. : Просвещение, 2009. – 464 с.
Алимов Ш. А. Алгебра и начала анализа : учебник для 10-11 классов средней школы / Ш. А. Алимов, Ю. М. Колягин, Ю. В. Сидоров [и др.] – М. : Просвещение, 2012. – 464 с.
Барчунова, Ф. М. Применение свойств функций при решении уравнений/ Ф. М. Барчунова, Л. О. Денищева // Математика в школе. 1992. № 6. С. 11.
Башмаков М. И. Алгебра и начала анализа: учебник для 10-11 классов средней школы / М. И. Башмаков [и др.] – СПб. : Свет, 1998. – 384 с.
Виленкин Н. Я. Алгебра и математический анализ для 11 класса: учебное пособие для учащихся школ и классов с углубленным изучением математики / Н. Я. Виленкин, О. С. Ивашев-Мусатов, С. И. Шварцбурд. – М. : Просвещение, 2012. – 288 с.
Виленкин Н. Я. Алгебра и математический анализ для 10 класса : учебное пособие для учащихся школ и классов с углубленным изучением математики / Н. Я. Виленкин, О. С. Ивашев-Мусатов, С. И. Шварцбурд. – М. : Просвещение, 2012. – 335 с.
9. Денищева Л. О. Проверка компетентности выпускников средней школы при оценке образовательных достижений по математике / Л. О. Денищева, Ю. А. Глазков, К. А. Краснянская // Математика в школе. – 2008. - №6. – C. 19-31.
10. Епишева О. Б. Технология обучения математике на основе деятельностного подхода: кн. для учителя / О. Б. Епишева. – М. : Просвещение, 2003. – 223 с.
11.Епишева, О. Б. Учить школьников учиться математике. Формирование приемов учебной деятельности: кн. для учителей / О. Б. Епишева, В. И. Крупич. – М. : Просвещение, 1990. – 128 с.
12.Кулабухов С. Ю. Математика. Подготовка к ЕГЭ-2012 : учебное пособие / С. Ю. Кулабухов/под Ред. Ф. Ф. Лысенко. − М. : Легион, 2012. − 416 c.
13.Мордкович, А. Г. Алгебра и начала анализа. 10-11 кл. : в 2 ч. Ч.1 : учеб. для общеобразоват. учреждений / А. Г. Мордкович – М. : Мнемозина, 2009. – 399 с.
Мордкович А. Г. Алгебра и начала анализа. 10-11 кл.: в 2 ч. Ч.2. : задачник для общеобразоват. учреждений / А. Г. Мордкович, Л. О. Денищева, Т. А. Корешкова [и др.]; под ред. А. Г. Мордковича – М. : Мнемозина, 2009. – 339 с.
15.Мордкович А. Г. Решаем уравнения / А. Г. Мордкович. – М. : Школа – Пресс, 1995. – 80 с.
16.Сайты ФИПИ, ЕГЭ, Алекс Ларин.
17.Эфендиев Э.И. Практикум по элементарной математике, Махачкала , 246с.
18. Ященко И. В. Подготовка к ЕГЭ по математике 2012-2016: учебное пособие / И. В. Ященко и др. − М. : МЦНМО, 2012 – 2016.







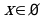 (т.е. решений нет).
(т.е. решений нет). 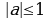 решения находятся по формуле
решения находятся по формуле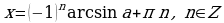 ( Напомним, что
( Напомним, что 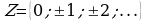 ).
).
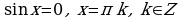

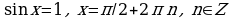

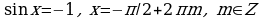
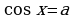
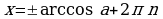 ,
, 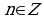

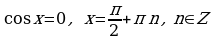

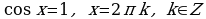

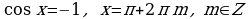
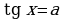 , для любого
, для любого 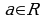
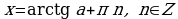
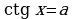 , для любого
, для любого 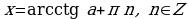
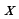
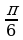
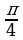
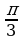
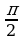
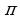
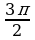
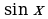
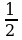
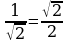
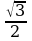
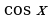
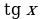
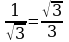
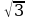
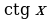
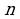 =0, 1, 2, 3, 4 – номера пальцев любой руки, а
=0, 1, 2, 3, 4 – номера пальцев любой руки, а 
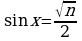 соответствующие значения
соответствующие значения 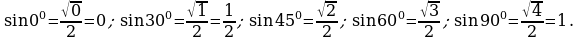
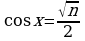 , соответственно,
, соответственно, 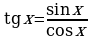 и
и 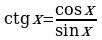 легко определяются по значениям
легко определяются по значениям 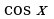 .
.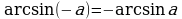 ,
, 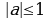 .
.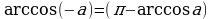 ,
, 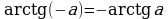 .
.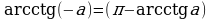 .
. 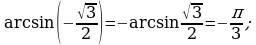
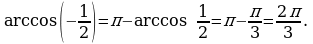
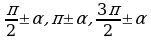 и
и 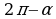 с тригонометрическими функциями угла
с тригонометрическими функциями угла 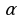 .
.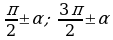 ), то наименование функции меняется на кофункцию (
), то наименование функции меняется на кофункцию (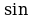 на
на 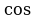 ,
, 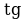 на
на 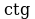 и т.д.);
и т.д.);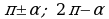 ), то наименование функции не меняется.
), то наименование функции не меняется.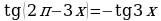
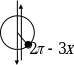 Наименование функции не изменилось, т.к. угол 3
Наименование функции не изменилось, т.к. угол 3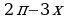 находится
находится 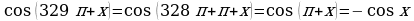
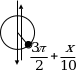 десь мы воспользовались, кроме формулы приведения, еще тем, что функция
десь мы воспользовались, кроме формулы приведения, еще тем, что функция 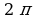 - периодической.
- периодической.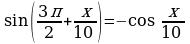
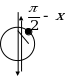
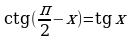

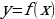 называется четной, если
называется четной, если 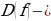 симметричное множество и
симметричное множество и 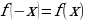 и нечетной, если
и нечетной, если 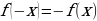 . У тригонометрических функций
. У тригонометрических функций 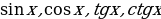 области определения симметричны, кроме того
области определения симметричны, кроме того 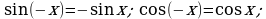
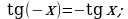
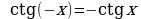 , поэтому
, поэтому 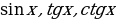 являются нечетными функциями, а
являются нечетными функциями, а 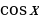 – четной функцией.
– четной функцией.
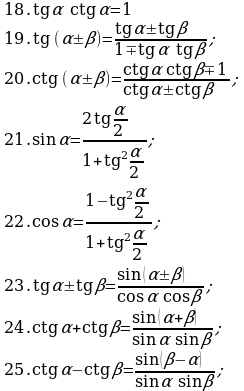
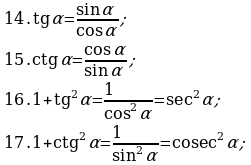
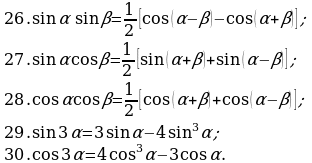
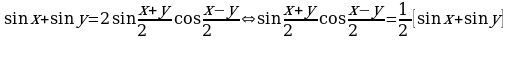
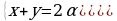 откуда
откуда 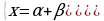 .
.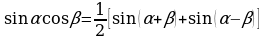 , т.е. формула 27 доказана.
, т.е. формула 27 доказана.
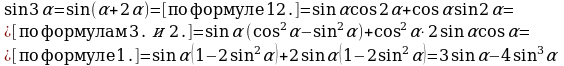
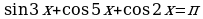
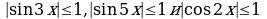 , то левая часть уравнения не может принимать значений больших, чем 3, а правая часть (
, то левая часть уравнения не может принимать значений больших, чем 3, а правая часть (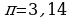 ...) больше 3. Поэтому данное уравнение не имеет корней.
...) больше 3. Поэтому данное уравнение не имеет корней. 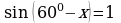
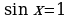 , т.к. недопустимо писать
, т.к. недопустимо писать 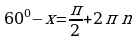 . Здесь возможны два варианта записи решения:
. Здесь возможны два варианта записи решения: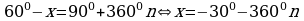 и поскольку
и поскольку 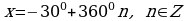 .
.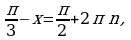
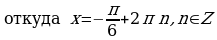 .
.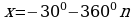 в виде
в виде 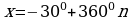 . Этих рассуждений можно было избежать, если бы мы воспользовались нечетностью синуса и запись решения осуществили бы в следующем виде:
. Этих рассуждений можно было избежать, если бы мы воспользовались нечетностью синуса и запись решения осуществили бы в следующем виде: 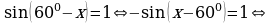
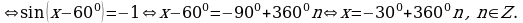
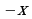 ”к “
”к “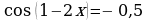 .
.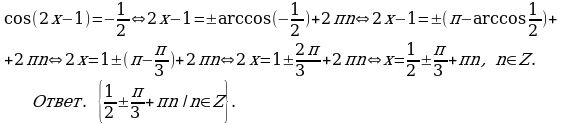
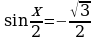
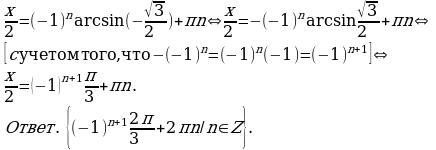
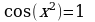 .
.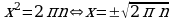
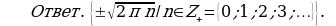
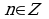 .
.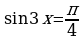 .
.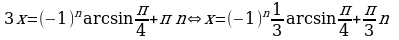
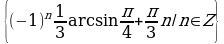 .
.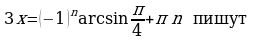
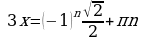
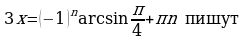
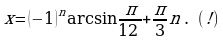 .
.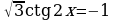 .
.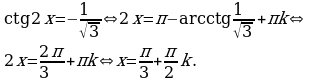
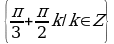 .
.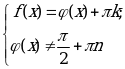
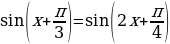 .
.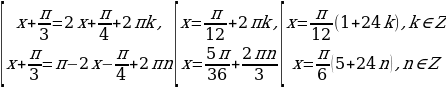
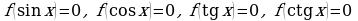 , решаются с помощью соответствующих подстановок
, решаются с помощью соответствующих подстановок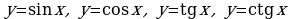 .
.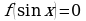 равносильно системе
равносильно системе 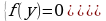
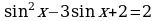 .
.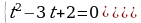 .
.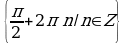 .
.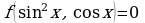 с помощью подстановки
с помощью подстановки 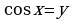 (откуда
(откуда 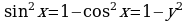 ) приводят к системе:
) приводят к системе: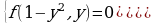
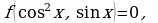
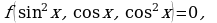
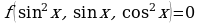 . С помощью соответствующих подстановок
. С помощью соответствующих подстановок 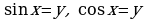 и
и 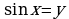 их приводят к системам:
их приводят к системам: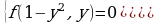 .
.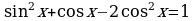 .
.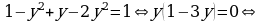
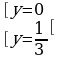 [возвращаясь к первоначальному обозначению]
[возвращаясь к первоначальному обозначению] 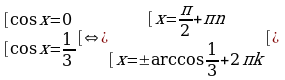 .
.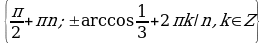 .
.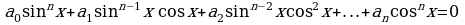 , (1)
, (1)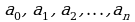 - действительные числа, называется однородным относительно
- действительные числа, называется однородным относительно 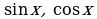 .
. 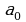 и
и 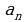 одновременно не равны нулю, то уравнение (1) называется однородным тригонометрическим уравнением
одновременно не равны нулю, то уравнение (1) называется однородным тригонометрическим уравнением 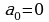 , то корни уравнения
, то корни уравнения 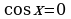 являются решениями уравнения (1).
являются решениями уравнения (1). 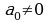 , то
, то 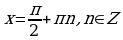 не являются решениями уравнения (1). Действительно, если
не являются решениями уравнения (1). Действительно, если 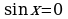 (т.к.
(т.к. 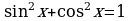 . Поэтому при
. Поэтому при 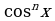 , не нарушая при этом равносильности. Тогда получим уравнение
, не нарушая при этом равносильности. Тогда получим уравнение 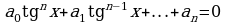 , которое решается подстановкой
, которое решается подстановкой 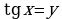 .
.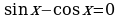 .
.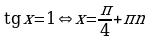
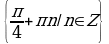 .
.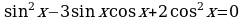 .
.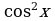 приводится к равносильному
приводится к равносильному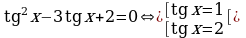
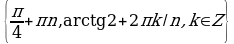 .
.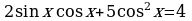 .
.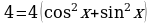 , получим равносильное уравнение
, получим равносильное уравнение 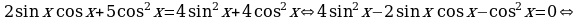
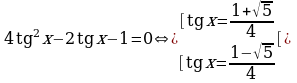 .
.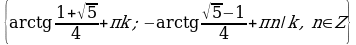 .
.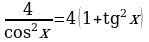 .
.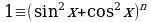 позволяет привести к однородным и следующее уравнение
позволяет привести к однородным и следующее уравнение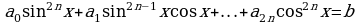 .
.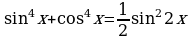 .
.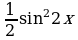 к виду
к виду 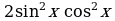 и решить полученное однородное уравнение четвертой степени обычным способом, но мы предложим другой способ:
и решить полученное однородное уравнение четвертой степени обычным способом, но мы предложим другой способ: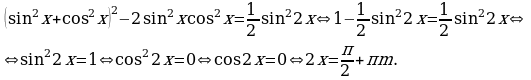
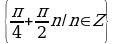 .
.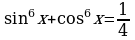 .
.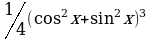 , то получим однородное уравнение 6ой степени. Снова приведем другое решение:
, то получим однородное уравнение 6ой степени. Снова приведем другое решение: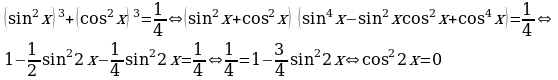 .
.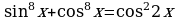 .
.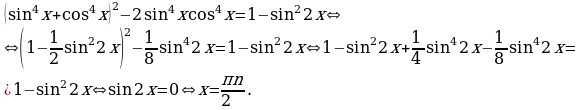
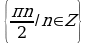 .
.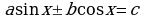 , (2)
, (2)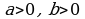 и
и 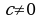 -действительные числа. (Если
-действительные числа. (Если 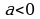 , то умножая обе части уравнения на (-1), приводим его к равносильному виду (2)).
, то умножая обе части уравнения на (-1), приводим его к равносильному виду (2)).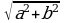 :
: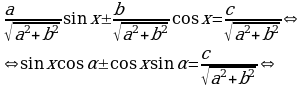
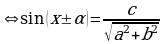 (3)
(3)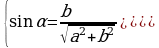 , откуда
, откуда 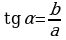
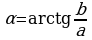 (учитывая, что
(учитывая, что 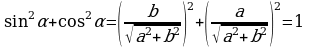 , то угол
, то угол 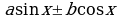 ,.
,.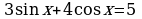 .
. 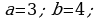
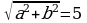 ;
; 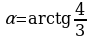 , следовательно, уравнение равносильно следующему:
, следовательно, уравнение равносильно следующему: 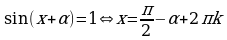 .
.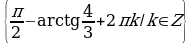 .
.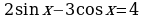 .
.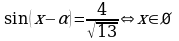 , т.к.
, т.к. 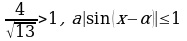 .
.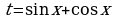 .
.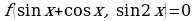 .
.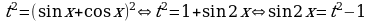 и данное уравнение равносильно системе:
и данное уравнение равносильно системе: 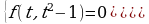 .
.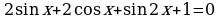 .
.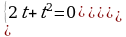
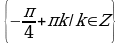 .
.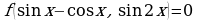 решаются подстановкой
решаются подстановкой 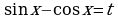 .
.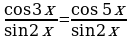 .
.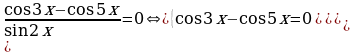 .
.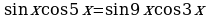 .
.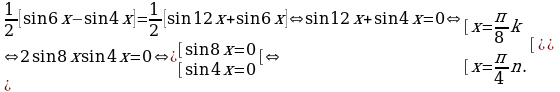
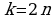 из
из 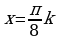 мы получаем
мы получаем 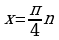 , т.е.
, т.е. 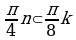 .
.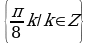 .
.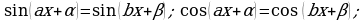
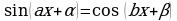 (с учетом того, что
(с учетом того, что 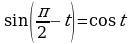 или
или 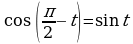 ) и некоторые другие уравнения.
) и некоторые другие уравнения.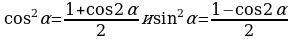
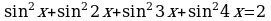 .
.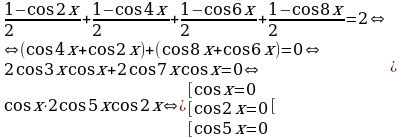
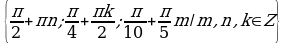 .
.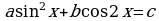 и
и 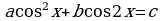 , а также более общее уравнение
, а также более общее уравнение 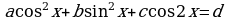 .
.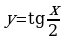 называется универсальной. С ее помощью решаются уравнения вида
называется универсальной. С ее помощью решаются уравнения вида 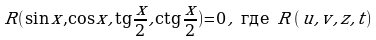 - рациональная функция своих аргументов. При этом
- рациональная функция своих аргументов. При этом 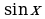 и
и 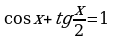 .
.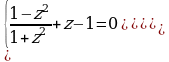 .
.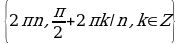 .
.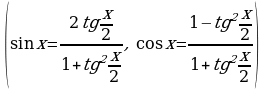 , теряют смысл при
, теряют смысл при 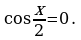 Поэтому при решении уравнений с помощью универсальной подстановки в первую очередь следует проверить, не являются ли значения
Поэтому при решении уравнений с помощью универсальной подстановки в первую очередь следует проверить, не являются ли значения 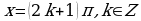 решениями данного уравнения.
решениями данного уравнения.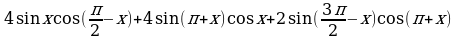
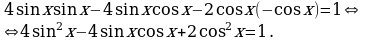
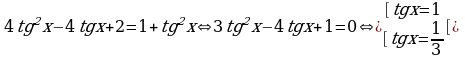
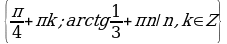 .
.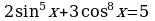 .
.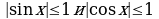 , то
, то 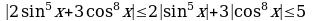 , причем равенство достигается только в том случае, если одновременно
, причем равенство достигается только в том случае, если одновременно 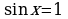 и
и 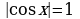 , что невозможно (т.к. нарушается основное тождество
, что невозможно (т.к. нарушается основное тождество 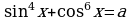 не имеет решения при
не имеет решения при 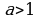 .
.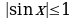 и
и 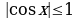 не приведут к цели. Поэтому воспользуемся неравенствами:
не приведут к цели. Поэтому воспользуемся неравенствами: 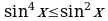 , а
, а 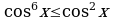 . Складывая почленно правые и левые части последних неравенств, получаем:
. Складывая почленно правые и левые части последних неравенств, получаем: 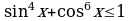 , откуда и следует, что исходное уравнение не имеет решения при
, откуда и следует, что исходное уравнение не имеет решения при 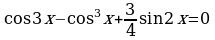 .
.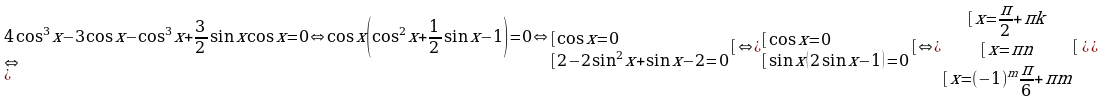 .
.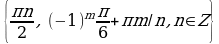 .
.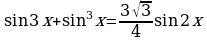 .
. 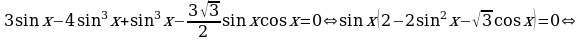
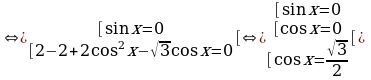 .
.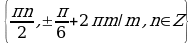 .
.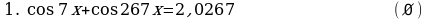
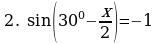
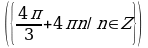
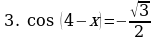
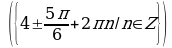
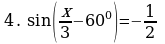
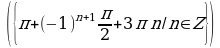
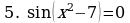
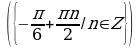
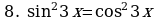
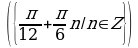
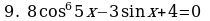
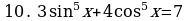
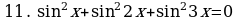
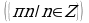
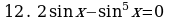
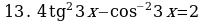
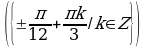
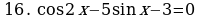
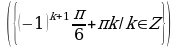
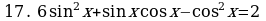
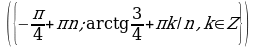
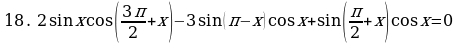
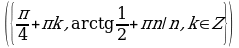
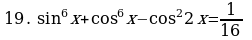
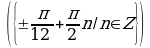
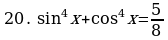
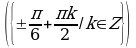
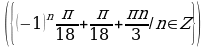
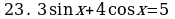
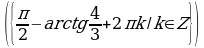
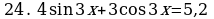
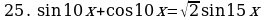
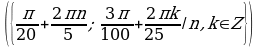
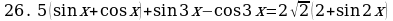
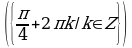
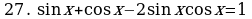
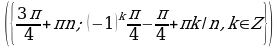
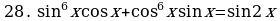
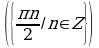
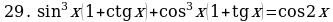
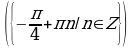
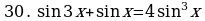
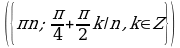
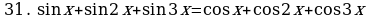
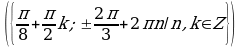
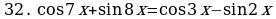
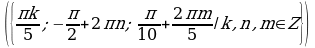
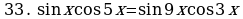
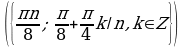
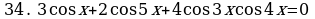
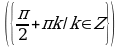
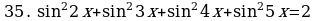
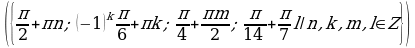
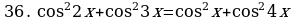
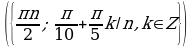
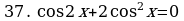
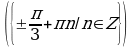
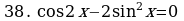
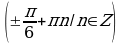
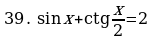
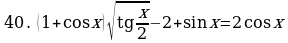
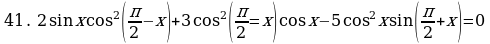
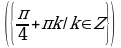
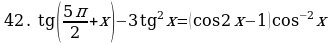
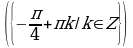
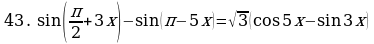
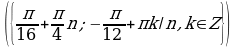
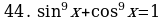
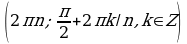
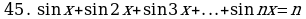
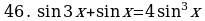
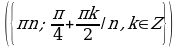
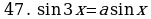
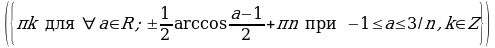
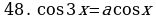
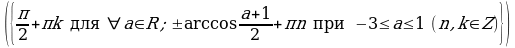
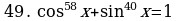
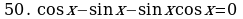
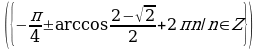
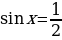 и найдите корни из промежутка
и найдите корни из промежутка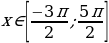 .
.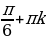 , k
, k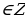 . Это означает, что x=30°+360°∙n или x=150°+360°∙n. Условие
. Это означает, что x=30°+360°∙n или x=150°+360°∙n. Условие 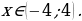
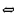
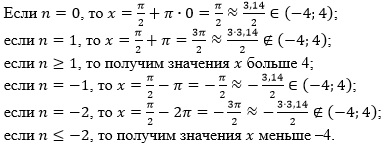
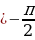 и х
и х 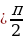
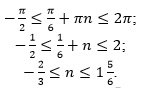
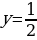 . Отметим такие точки, выделив фрагмент графика на промежутке .
. Отметим такие точки, выделив фрагмент графика на промежутке .















