Методическое пособие "Теорема Морли"

Муниципальное автономное общеобразовательное учреждение "Лицей №14 имени Заслуженного учителя Российской Федерации А.М. Кузьмина"

Методическое пособие

по теме:

«Теорема Морли»

Выполнил ученик 10-А класса Березняк А. А.

Тамбов, 2021

Оглавление

Введение ……………………………………………………………………..3

История изучения теоремы Морлея………………………………………...4

Доказательства теоремы Морлея……………………………………………5

Применение теоремы Морлея при решении задач………………………..10

Упражнения для самостоятельного решения…………………………...…11

Введение

Треугольник – одна из самых простых геометрических фигур: три стороны и три вершины. Еще математиками в глубокой древности были открыты и изучены многие свойства треугольников. Но оказалось, что простая геометрическая фигура таит в себе еще множество открытий. Интересные факты о треугольнике открывались на протяжении всей истории их изучения.

Первые упоминания о треугольнике и его свойствах найдены в папирусах Древнего Египта. А именно: там описан способ нахождения площади равнобедренного треугольника. В Древней Греции изучение свойств треугольника выходит на новый уровень. Пифагор открывает свою известнейшую теорему. Герон Александрийский находит формулу, выражающую площадь треугольника через его стороны; становится известным, что биссектрисы, как медианы и высоты, пересекаются в одной точке.

В XV – XVI веках особенно активно исследовались свойства треугольника. Эти исследования составили большой раздел планиметрии, получивший название «Новая геометрия треугольника».

История изучения теоремы Морлея

Франк Морлей (9 сентября 1860 — 17 октября 1937) — математик, внёсший большой вклад в алгебру и геометрию. Родился в городке Вудбридж в графстве Саффолк. Родители владели небольшим магазином фарфора. В 1884 году окончил Кингс-колледж в Кембридже, в 1887 году уехал в США, но оставался британским подданным. До 1900 года преподавал в Хэверфордском колледже (Пенсильвания), потом получил кафедру в Университете Джонса Хопкинса в Балтиморе. Был широко известен как математик, в 1919—1920 годах был президентом Американского математического общества, а с 1900 по 1921 год — редактором ведущего математического журнала American Journal of Mathematics.

Наиболее известным результатом Фрэнка Морли является знаменитая теорема о трисектрисах его имени, гласящая, что точки пересечения смежных трисектрис углов произвольного треугольника являются вершинами равностороннего треугольника. [1]

Доказательство теоремы о трисектрисах Морлей опубликовал в 1914 году – через 15 лет после того, как нашел его. В 1924 году он изложил это доказательство более подробно и существенно усилил первоначальный результат. Доказательство Морлея весьма элегантно, но в то же время достаточно сложно. Оно базируется на рассмотрении довольно изысканных линий – так называемых кардиоид.

Первые элементарные доказательства теоремы Морлея были получены в 1909 году индусами М. Сатьянараяном и М. Т. Нараньенгаром. В настоящее время известно уже, по крайней мере, несколько десятков доказательств теоремы Морлея. Однако интерес к ней не затухает, и все время появляются новые доказательства, обобщения и варианты этого изящного предложения.

Доказательства теоремы Морлея

Первое доказательство

У этой теоремы есть, к сожалению, один существенный «недостаток». До недавнего времени были известны лишь довольно сложные доказательства этой теоремы. Ниже предлагается два коротких доказательства, найденных не так давно.

Доказательство теоремы Морлея

Пусть АВС – данный треугольник, а треугольник XYZ образован трисектрисами углов данного треугольника (рис.1). Докажем, что треугольник XYZ равносторонний.

Рис. 1

Введем обозначения: ∠А = 3α, ∠В = 3β, ∠С = 3γ. Рассмотрим произвольный равносторонний треугольник A₁B₁C₁ (рис. 2).

Рис. 2

Построим на стороне B₁C₁ треугольник A₂B₁C₁ так, чтобы ∠A₂B₁C₁=γ+60⁰, а ∠A₂C₁B₁=β+60°. Очевидно, что ∠ B₁A₂C₁= α , так как α + β + γ = 60°.

Точно так же построим еще два треугольника A₁C₁B₂ и A₁B₁C₂ (см. рис.2).

Лучи A₂ B₁ и B₂ A₁ пересекутся в некоторой точке М, так как сумма углов B₁A₂B₂ и A₁B₂A₂ меньше 180 градусов. При этом для треугольника A₂B₂M выполняются условия задачи 3. Поэтому A₂C₁ будет биссектрисой угла B₁A₂B₂, а B₂C₁ будет биссектрисой угла A₁B₂A₂. Это означает, что ∠ C₁A₂B₂ = α, а ∠C₁B₂A₂= β.

Аналогичный результат получается и в остальных случаях (для A₂B₁, C₂B₁, C₂A₁ и B₂A₁).

Таким образом, оказывается, что в треугольнике A₂B₂C₂ проведены трисектрисы, и они при своем пересечении определяют равносторонний треугольник. Но очевидно, что треугольники A₂B₂C₂ и АВС подобны (по углам). Следовательно, и треугольник XYZ также равносторонний. Теорема Морлея доказана. [3]

Второе доказательство (Доказательство Конвея)

Пусть углы исходного треугольника равны 3α, 3β, 3γ. Введем удобное обозначение: будем писать ϕ^∗ вместо ϕ + 60°. Тогда α + β + γ = 0^∗. Заметим, что существуют треугольники с углами (0^∗, 0^∗, 0^∗), (α, β^∗, γ^∗), (α^∗, β, γ^∗), (α^∗, β^∗, γ), (α^∗∗, β, γ), (α, β^∗∗, γ), (α, β, γ^∗∗), так как в каждом случае сумма углов равна 180°. Теперь для каждой тройки углов построим конкретный треугольник с этими углами, специально подбирая длины сторон.

Для тройки (0∗, 0∗, 0∗) это будет равносторонний треугольник со стороной 1.

Для тройки (α^∗, β, γ^∗) – это треугольник, в котором сторона, соединяющая вершины с углами α^∗ и γ^∗, равна 1 (рис.3, а). Аналогично поступим с тройками (α, β^∗, γ^∗) и (α^∗, β^∗, γ).

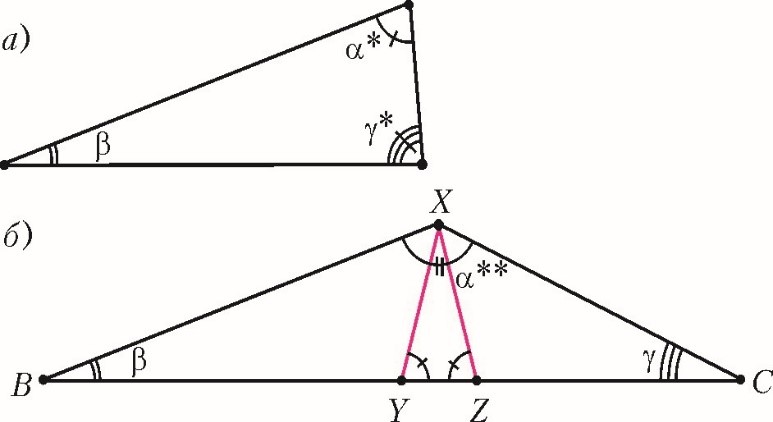
Рис 3

Для тройки (α^∗∗, β, γ) сделаем так. Рассмотрим треугольник BXC (рис.3, б), в котором угол при вершине B равен β, при вершине X равен α^∗∗, а при вершине C равен γ. Через вершину X проведем два луча, которые пересекают прямую BC в точках Y и Z под углом α^∗, и подберем масштаб так, чтобы XY = XZ = 1. При этом сторона BX окажется равной стороне, лежащей против угла α^∗ в уже построенном треугольнике с углами α^∗, β, γ^∗. Аналогично построим треугольники и для двух оставшихся троек такого вида.

Итак, мы получили 7 треугольников. Расположим их как показано на рисунке 4, и начнем придвигать их друг к другу, чтобы получился рисунок 5. Почему все так хорошо совпадет? Во-первых, суммы углов при всех внутренних вершинах равны 360°. Во-вторых, красный треугольник примыкает к зеленым по единичным отрезкам, а желтые треугольники примыкают к зеленым по равным отрезкам по построению (выше мы доказали это для треугольника BXC и треугольника с углами α^∗, β, γ^∗, аналогично рассматривается любая пара из желтого и зеленого треугольников).

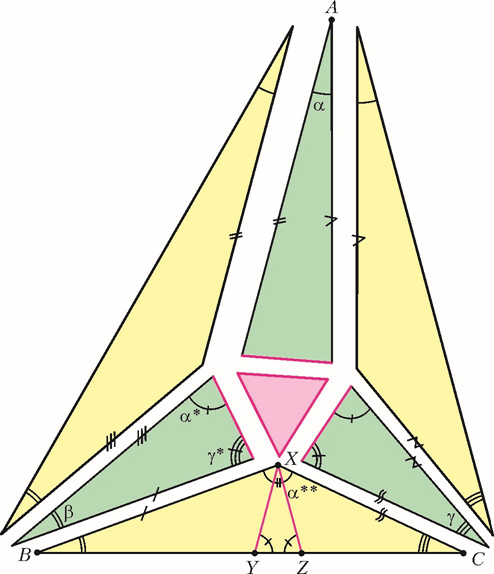
Рис. 4

Рис. 5

Образовавшийся треугольник ABC подобен исходному по трем углам, а получившаяся картинка совпадает с той, что получится при проведении трисектрис. Поэтому и в исходном треугольнике образованный трисектрисами треугольник будет равносторонним. [3]

Применение теоремы Морлея при решении задач

Задача 1

Д ано: ΔABC, AZ, CZ, AQ, BQ, CD, BD трисектрисы, QD=12.

Найти: SΔZQD

Рис. 6

Решение:

1)По теореме Морли ΔZQD равносторонний так как AZ, CZ, AQ, BQ, CD, BD трисектрисы.

2)По формуле площади равностороннего треугольника S=√3 * QD /4=√3

Ответ:36√3

Задача 2

Д ано: ΔABC равносторонний, AZ, CZ, AQ, BQ, CD, BD трисектрисы.

Доказать: ΔAZQ=ΔBQD= ΔCZD.

Рис.7

Решение:

1)Так как ΔABC равносторонний, то все углы, образованные трисектрисами равны. Следовательно, ZAC=ZAQ=QAB=ZCA=ZCD=DCB=CBD=DBQ=QBA

2)Рассмотрим ΔAZC, ΔBQA и ΔCDB они равны так как AC=AB=BC по свойству равностороннего треугольника

ZAC=ZAQ=QAB=ZCA=ZCD=DCB=CBD=DBQ=QBA Следовательно, ΔAZC=ΔBQA=ΔCDB

3)ΔAZC=ΔBQA=ΔCDB следует AZ=ZC=AQ=BQ=DB=CD

4)Рассмотрим ΔAZQ, ΔBQD и ΔCZD

AZ=ZC=AQ=BQ=DB=CD

AC=AB=BC по свойству равностороннего треугольника

Следовательно, ΔAZQ=ΔBQD= ΔCZD.

Упражнения для самостоятельного решения

1. Дано ΔABC AZ, CZ, AQ, BQ, CD, BD трисектрисы углов ΔABC, QD=12. Найдите площадь ΔZQD.

2. Дано ΔABC равносторонний, AZ, CZ, AQ, BQ, CD, BD трисектрисы углов ΔABC.

Докажите: ΔAZQ=ΔBQD= ΔCZD.

3. Дано ΔABC равнобедренный AC основание, AZ, CZ, AQ, BQ, CD, BD трисектрисы углов ΔABC, угол AZC=140.

Докажите: ΔAZQ=ΔBQD= ΔCZD.

4. Дано ΔABC равнобедренный AC основание, BQ трисектриса, прилегающая к стороне AB, а BD трисектриса, прилегающая к стороне BC угла ABC, ΔAZC равнобедренный угол AZC=140, угол BAQ=QAZ=ZAC.

Докажите: ΔAZQ=ΔBQD= ΔCZQ.

5. Дано ΔABC равнобедренный AC основание, BQ трисектриса, прилегающая к стороне AB, а BD трисектриса, прилегающая к стороне BC угла ABC, ΔAZC равнобедренный угол AZC=150, угол BAQ=QAZ=ZAC, QD=12, AC=36, AQ=13.

Найдите площадь четырехугольника AQZC.

6. Дано ABCD ромб, BQ трисектриса, прилегающая к стороне AB, а BW трисектриса, прилегающая к стороне BC угла ABC, ΔAZC равнобедренный угол AZC=160, угол BAQ=QAZ=ZAC, DK трисектриса, прилегающая к стороне AD, а DF трисектриса, прилегающая к стороне DC угла ADC, ΔAJC равнобедренный угол AJC=160, угол BAQ=QAZ=ZAC.

Докажите QW параллельна KF.

7. Дано ABCD ромб, BQ трисектриса, прилегающая к стороне AB, а BW трисектриса, прилегающая к стороне BC угла ABC, ΔAZC равнобедренный угол AZC=156, угол BAQ=QAZ=ZAC, DK трисектриса, прилегающая к стороне AD, а DF трисектриса, прилегающая к стороне DC угла ADC, ΔAJC равнобедренный угол AJC=156, угол BAQ=QAZ=ZAC.

Докажите QWFK-параллелограмм.

8. Дано ABCD ромб, BQ – трисектриса, прилегающая к стороне AB, а BW трисектриса, прилегающая к стороне BC угла ABC, ΔAZC равнобедренный угол AZC=156, угол BAQ=QAZ=ZAC, DK трисектриса, прилегающая к стороне AD, а DF трисектриса, прилегающая к стороне DC угла ADC, ΔAJC равнобедренный угол AJC=156, угол BAQ=QAZ=ZAC.

Докажите QWFK-прямоугольник.

9. Дано ABCD прямоугольник, BQ – трисектриса, прилегающая к стороне AB, а BW трисектриса, прилегающая к стороне BC угла ABC, ΔAZC равнобедренный угол AZC=150, угол BAQ=QAZ=ZAC, DK трисектриса, прилегающая к стороне AD, а DF трисектриса, прилегающая к стороне DC угла ADC, ΔAJC равнобедренный, угол AJC=150, угол BAQ=QAZ=ZAC.

Докажите, что QWFK-прямоугольник.

10. Дано ABCD прямоугольник, BQ трисектриса, прилегающая к стороне AB, а BW трисектрис, а прилегающая к стороне BC угла ABC, ΔAZC равнобедренный угол AZC=150, угол BAQ=QAZ=ZAC, DK трисектриса прилегающая к стороне AD, а DF трисектриса прилегающая к стороне DC угла ADC, ΔAJC равнобедренный, угол AJC=150, угол BAQ=QAZ=ZAC, QW=12, AC=36, AQ=13.

Докажите, что QWFK-прямоугольник и найдите его периметр.

11. Дано ABCD ромб, BQ трисектриса, прилегающая к стороне AB, а BW трисектриса, прилегающая к стороне BC угла ABC, ΔAZC равнобедренный угол AZC=154, угол BAQ=QAZ=ZAC, DK трисектриса прилегающая к стороне AD, а DF трисектриса прилегающая к стороне DC угла ADC, ΔAJC равнобедренный угол AJC=150, угол BAQ=QAZ=ZAC, QW=12, AC=36, AQ=13.

Докажите, что QWFK - прямоугольник и найдите его площадь.

12. Дано ΔABC AZ, CZ, AQ, BQ, CD, BD трисектрисы углов ΔABC, углы AZC=140, AQB=168. Найдите углы Δ ABC. (задача с трисектрисами)

13. Дано ΔABC AZ, CZ, AQ, BQ, CD, BD трисектрисы углов ΔABC, углы AZQ=50, DZC=90, BQD=40. Докажите ΔABC равнобедренный.

14. Дано ΔABC AZ, CZ, AQ, BQ, CD, BD трисектрисы углов ΔABC, угол ABC=3b, ACB=3c, BAC=3a, радиус описанной окружности R.

Найдите ZQ.

10