Методика формирования и использования координатного и векторного методов в школьном курсе математики.

Тема: Методика формирования и использования координатного и векторного методов в школьном курсе математики.

Цели: Определить цели и учебные задачи введения и использования координатного и векторного методов в школьном курсе математики, систематизировать понятного аппарата по координатному и векторному методам, раскрыть специфику использования координатного и векторного методов в школьных курсах алгебры и геометрии, проанализировать школьные учебники по вопросам формирования и использования координатного и векторного методов.

Общие вопросы и задания:

1.Цели и учебные задачи координатного метода в школе.

Цели изучения координатного метода в школьном курсе геометрии:

• дать учащимся эффективный метод решения задач и доказательства ряда теорем;

• показать на основе этого метода тесную связь алгебры и геометрии;

• способствовать развитию вычислительной и графической культуры учащихся.

Задачи:

1. переводить геометрический язык на аналитический;

2. строить точку по заданным координатам;

3. находить координаты заданных точек;

4. вычислять расстояние между точками, заданными координатами;

5. вычислять расстояние между прямой и плоскостью, прямыми и

плоскостями;

6. вычислять угол между прямой и плоскостью, прямыми и плоскостями;

7. оптимально выбирать систему координат;

8. составлять уравнения заданных фигур (плоскости и прямые) и

вычислять определитель;

9. видеть за уравнением конкретный геометрический образ;

10. выполнять преобразование алгебраических соотношений

2. Цели изучения векторного метода в средней школе:

 дать эффективный метод решения различных геометрических задач (как аффинных, так и метрических) и доказательства теорем;

 показать широкое применение векторного аппарата в других областях знаний: технике, физике, химии, лингвистике – и на базе этого расширять их кругозор и формировать мировозрение;

 использовать векторный метод при решении задач с целью форматирования у учащихся выполнять обобщение и конкретизацию;

 формировать у учащихся такие качества мышления, как гибкость (нешаблонность), целенаправленность, рациональность, критичность и др.

Задачи:
1) перевод условия задачи на язык векторов, в том числе:

• введение в рассмотрение векторов;

• выбор базисных векторов;

• разложение всех введенных векторов

1. составление системы векторных равенств (или одного равенства).

2. упрощение векторных равенств

3. замена векторных равенств алгебраическими уравнениями и их решения

4. объяснение геометрического смысла полученного решения этой системы (или одного уравнения).

3. Понятийный аппарат.

 На первом этапе вводится основной понятийный аппарат, который хорошо отрабатывается в 5-6 классах и систематизируется в курсе геометрии. В 5 классе учащиеся знакомятся с координатным лучом, который в последствии, при изучении отрицательных чисел, дополняется до координатной прямой. И уже после введения  рациональных чисел в 6 классе учащиеся изучают координатную плоскость. На втором этапе ученики знакомятся с  уравнениями прямой и окружности. Данные понятия изучаются ими как в алгебре, так и в геометрии с разной содержательной целью, поэтому учащиеся часто не видят связи между ними, а, значит, и плохо усваивают суть метода. Так, в курсе алгебры VII класса графики основных функций вводятся путем построения ряда точек, координаты которых вычисляются по аналитическому заданию функции. 

Понятийный аппарат, которым должен овладеть ученик, чтобы научиться решать геометрические задачи векторным методом в основной школе:

 основные понятия: вектор, начало вектора, конец вектора, одинаково направленные векторы, противоположно направленные векторы, абсолютная величина вектора (модуль вектора), равные векторы, нулевой вектор, неколлинеарные векторы.

4. Компоненты векторного метода.

Для решения задач учащиеся должны владеть следующими умениями, которые и являются компонентами векторного метода:

1. перевод условия задачи на язык векторов, в том числе:

   • введение в рассмотрение векторов;

   • выбор базисных векторов;

   • разложение всех введенных векторов

2. составление системы векторных равенств (или одного равенства).

3. упрощение векторных равенств

4. замена векторных равенств алгебраическими уравнениями и их решения

5. объяснение геометрического смысла полученного решения этой системы (или одного уравнения).

5. Этапы формирования векторного метода у учащихся.

1. дать эффективный метод решения различных геометрических задач (как аффинных, так и метрических) и доказательства теорем;

2. показать широкое применение векторного аппарата в других областях знаний: технике, физике, химии, лингвистике – и на базе этого расширять их кругозор и формировать мировозрение;

3. использовать векторный метод при решении задач с целью форматирования у учащихся выполнять обобщение и конкретизацию;

4. формировать у учащихся такие качества мышления, как гибкость (нешаблонность), целенаправленность, рациональность, критичность и др.

Координатный метод решения задачи.

Задача. Дана прямоугольная трапеция с основаниями a и b. Найдите расстояние между серединами ее диагоналей. (Атанасян, Геометрия 10 -11 класс)

Решение. 1. Введем систему координат как указано на рисунке 3. Тогда вершины трапеции будут иметь координаты: A(0,0), B(0,y), C(b,y) и D(a,0). (Здесь y – высота трапеции).

2. Найдем координаты середин диагоналей, используя формулу (2), и учитывая, что середина делит отрезок в отношении l=1. Для точки О: . Для точки О₁: . По формуле (6) найдем расстояние между точками О и О₁:

.

Ответ: .

Замечание. Мы вводили в рассмотрение неизвестную нам высоту трапеции y. Но на этапе вычислений она сократилась.

Векторно-координатный метод решения задачи.

Задача. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ рёбра АВ и АА₁ равны 1, а ребро АD=2. Точка Е – середина ребра В₁С₁. Найдите угол между прямой ВЕ и плоскостью (АВ₁С).(Атанасян, Геометрия 10-11класс).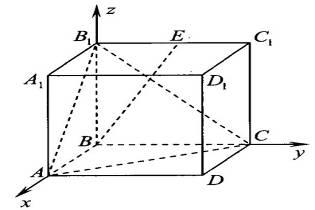

Решение: Составим уравнение плоскости (АВ₁С.):

ах+bу+cz+d=0, где a, b и c – координаты нормали к плоскости.

Чтобы составить это уравнение, необходимо определить координаты трёх точек, лежащих в данной плоскости: А(1; 0; 0), В₁(0;0;1), С(0;2;0).

Решая систему

находим коэффициенты а, b и с уравнения ах+bу+cz+d=0: а= -d, b=, c=-d. Таким образом, уравнение примет вид или, после упрощения, 2х+у+2z-2=0. Значит, нормаль n к этой плоскости имеет координаты .

Найдем координаты вектора

Найдем угол между вектором и нормалью к плоскости по формуле скалярного произведения векторов:

.

Ответ: 45˚