Методика работы с заданием, направленным на отработку связей между скоростями при движении по реке

Методика работы с заданием, направленным на отработку связей между скоростями при движении по реке

Учебник: С. М. Никольский и др., страница 122.

Класс: 5

Цель: отработать связи между скоростями при движении по реке

Дидактические средства:

• компьютерная презентация;

• учебник.

Ход фрагмента урока:

1. Анализ условия задачи

   Деятельность учителя	Деятельность учащихся
   - Ребята, посмотрите задачу № 544. Что необходимо сделать?	- Заполнить пропуски в таблице
   - Внимательно посмотрите на таблицу и скажите, с какой темой связана таблица?	- Движение по реке.
   - Что дано в первой строчке таблицы?	- Собственная скорость и скорость течения.
   - Что требуется найти?	- Скорость по течению реки и скорость против течения реки.
   - Сформулируйте задачу, соответствующую первой строчке таблицы.	-Найдите скорость по течению реки и скорость против течения реки, если известна собственная скорость и скорость течения.

2. Поиск способа решения

   - Хватает ли нам данных, чтобы заполнить первую строчку таблицы?	- Да.
   - Что мы можем найти по данным задачи?	- Скорость по течению реки.
   - Как это сделать?	- К собственной скорости прибавить скорость течения.
   - Хорошо! Как найти скорость против течения?	- Как разность собственной скорости и скорости течения.
   - Итак, какие три вопроса мы себе задавали при решении задачи, соответствующей первой строчке таблицы?	- 1) Что дано? 2) Что требуется найти? 3) Как это сделать?
   - Самостоятельно заполните оставшиеся пропуски в таблице, используя эти вопросы.

3. Проверка заполнения таблицы

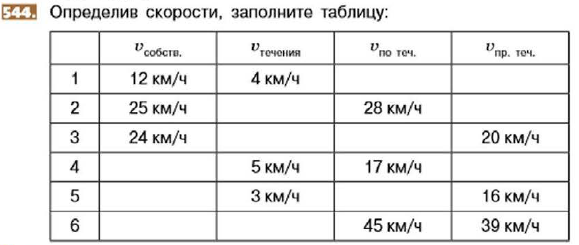
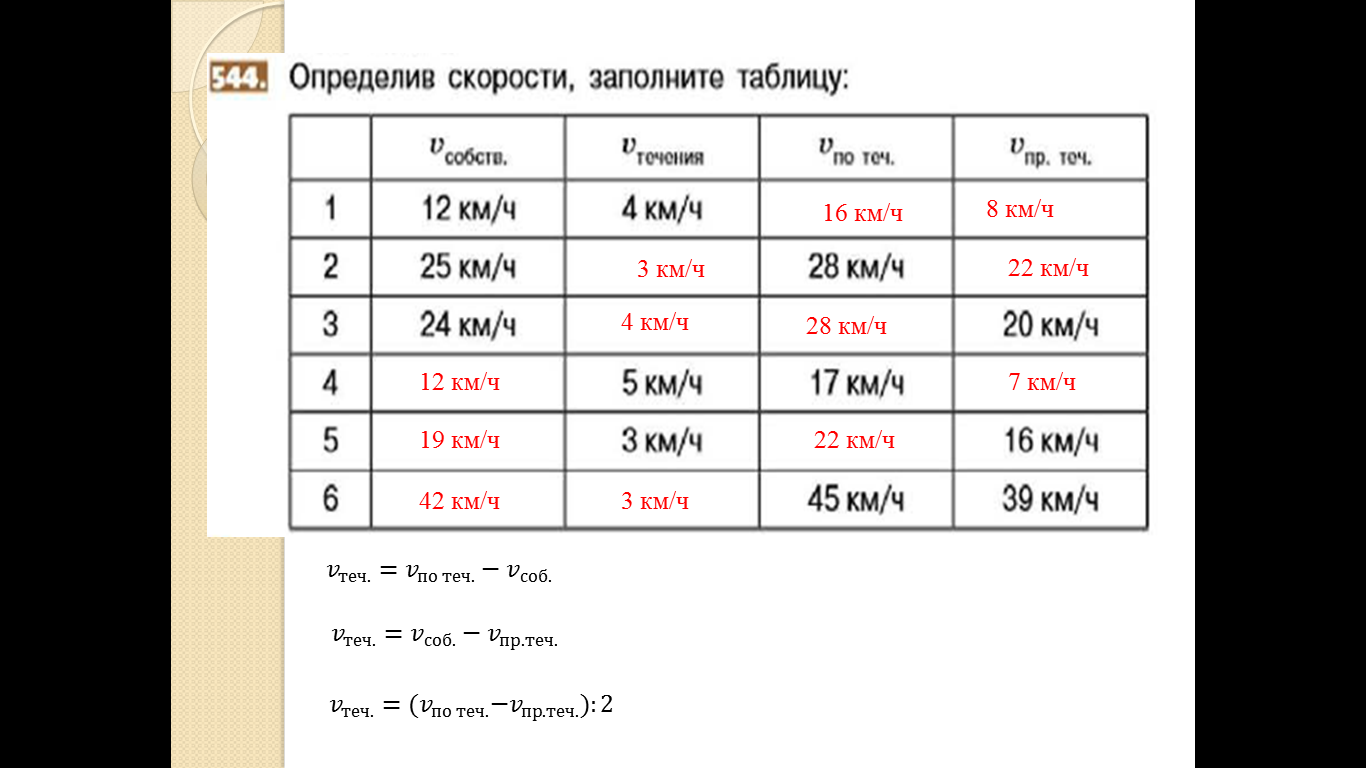
   - Итак, проверяем! Столкнулись ли Вы с затруднениями при заполнении второй строчки таблицы?	- Нет
   - Что требовалось?	- 1) Найти скорость течения; 2) найти скорость против течения .
   - Верно! Как Вы находили скорость течения?	- Как разность скорости по течению и собственной скорости.
   - Как находили скорость против течения?	- Как разность собственной скорости и скорости течения.
   - Молодцы! Что находили, используя данные четвёртой строчки?	- Собственную скорость.
   - Как?	- Вычитанием из скорости по течению реки скорости течения.
   - Как находили скорость против течения?	- Из собственной скорости вычли скорость течения .
   - Возникали ли трудности при заполнении пятой строчки таблицы?	- Нет.
   - Что требовалось?	- Найти собственную скорость, а затем найти скорость по течению.
   - Как найти собственную скорость, используя данные пятой строчки?	- Сложить скорость против течения со скоростью течения.
   - Почему?	- Поскольку скорость против течения равна разности собственной скорости и скорости течения, то собственная скорость равна сумме скорости против течения и скорости течения
   - Как находили скорость по течению реки?	- Сложили собственную скорость со скоростью течения.
   - Молодцы! Столкнулись ли Вы с проблемами при заполнении последней строчки таблицы?	- Да.
   - Давайте разбираться. Составьте задачу, соответствующую последней строчке таблицы.	- Найдите собственную скорость и скорость течения, если известны скорость по течению реки и скорость против течения реки.
   - Какие три вопроса мы задаём при решении задач?	- Что дано? Что требуется найти? Как это сделать?
   - Что дано?	- Скорость по течению и скорость против течения.
   - Что требуется найти?	- Собственную скорость и скорость течения.
   - Давайте изобразим скорости по и против течения с помощью отрезков. Я на доске, а Вы в тетрадях. Как Вы думаете, какая скорость больше?	- Скорость по течению.
   - Значит отрезок, соответствующий скорости по течению реки нарисуем длиннее. (Учитель рисует отрезок на доске)
   - Из чего состоит скорость по течению?	- Из собственной скорости и скорости течения.
   - Отметим на отрезке собственную скорость и скорость течения vт vc
   - Под этим отрезком нарисуем отрезок, соответствующий скорости против течения. Но сначала скажите, чему равна скорость против течения?	- Разности собственной скорости и скорости течения.
   - Что мы можем сказать о втором отрезке? Как его изобразить?	- Начертить отрезок, соответствующий собственной скорости, и на нём отметить отрезок скорости течения. Разность отрезков и будет соответствовать отрезку скорости против течения.
   - Молодцы! vc vт vпр.т. vт
   - Какой вывод мы можем сделать, глядя на чертёж?	- Скорость по течению больше скорости против течения на две скорости течения.
   - Итак, что мы можем найти по данным задачи?	- Удвоенную скорость течения.
   - Как это сделать?	- Из скорости по течению вычесть скорость против течения.
   - Как теперь найти скорость течения?	- Полученное число разделить пополам.
   - Сможем ли теперь найти собственную скорость?	- Да.
   - Как?	- Либо как разность скорости по течению и скорости течения, либо как сумму скорости против течения и скорости течения.
   - Молодцы! Оформите решение последней строчки в тетради.

4. Подведение итогов

На этапе проверки заполнения таблицы на экране представлена презентация с таблицей. С помощью анимации заполняется таблица. Учащиеся сверяют свои ответы с предложенными и задают вопросы, если возникли трудности.

Комментарий:

Задание данного типа реализует деятельностный подход, поскольку с помощью него можно находить связь между скоростями при движении по реке. Анализ условия предполагает формулировку общих вопросов. Поиск способа решения показывает учащимся на примере первой строчки, как нужно решать такого рода задания. В ходе решения учащиеся сталкиваются с проблемной ситуацией (приём личностно ориентированного обучения), в ходе решения которой приходят к открытию нового математического факта. Для проверки заполнения таблицы используется презентация, которая содержит таблицу, соответствующую заданию. Ответы в таблице появляются после ответов учащихся с помощью анимации на этапе проверки.