Просмотр содержимого документа
«Методы анализа и прогнозирования временных рядов. Трендовый анализ. Методы выявления тренда.»
Теоретические основы статистического анализа. Методы анализа и прогнозирования временных рядов
6 Трендовый анализ
Выявление аномальных уровней ряда
Для выявления аномальных уровней ряда в курсовом проекте используется метод Ирвина:
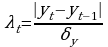
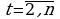 ,
, 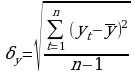 ,
, 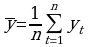
λ2, λ3, λ4 сравнивают с табличным значением критерия Ирвина λα и если
λt λα , то соответствующий yt – аномальный уровень. Для курсовой работы при числе наблюдений n=24, табличное значение критерия Ирвина равно 1,25.
После выявления аномальных уровней обязательно выявляется причина их возникновения. Если аномальные уровни относятся к ошибкам первого рода, то их устраняют следующим образом:
Заменой аномального уровня yt простой арифметической двух соседних уровней ряда 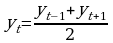 ;
;
Соответствующими значениями на кривой аппроксимирующей данный временной ряд.
7 Методы выявления тренда
Метод разности средних
Основой алгоритма является проверка по нулевой гипотезе (отсутствует тенденция развития) разности двух средних уровней:
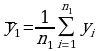 и
и 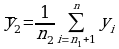
(n1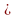 n2, n1+n2 = n)
n2, n1+n2 = n)
За критерий проверки берется t-критерий Стьюдента.
Расчетное значение определяется:
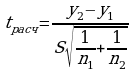 ,
,
где S – средневзвешенное значение среднеквадратичных отклонений относительно 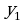 и
и 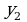 .
.
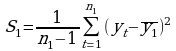 ;
; 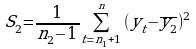 ;
;
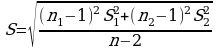 .
.
Теоретическое значение t-критерия Стьюдента находят по таблице при k=n-2.
Если 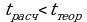 , гипотеза принимается
, гипотеза принимается
Если 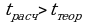 , гипотеза отвергается, тенденция развития есть.
, гипотеза отвергается, тенденция развития есть.
Метод Фостера-Стюарта
Основу метода составляют 2 характеристики
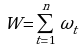 и
и 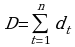 ,
,
где 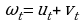 ,
,
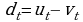 ,
,
параметры 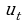 и
и 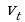 находят по формулам
находят по формулам
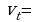
Показатель W применяется для определения тенденции изменения во времени дисперсии, а показатель D – средней. Проверяются нулевая гипотеза по t-критерию Стьюдента об отсутствии тенденции развития средней (или дисперсии).
Для проверки гипотез находят расчетные значения:
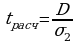 ,
,
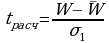 ,
,
где 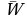 - среднее значение параметра W;
- среднее значение параметра W;
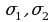 -среднеквадратичные ошибки W и D.(эти значения берутся из таблиц)
-среднеквадратичные ошибки W и D.(эти значения берутся из таблиц)
Если 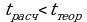 , гипотеза принимается
, гипотеза принимается
Если 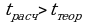 , гипотеза отвергается, тенденция развития есть.
, гипотеза отвергается, тенденция развития есть.
Прежде, чем приступить к выбору аппроксимирующей функции исходный динамический ряд необходимо сгладить.







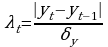
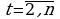 ,
, 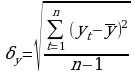 ,
, 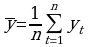
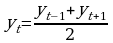 ;
;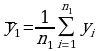 и
и 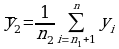
 n2, n1+n2 = n)
n2, n1+n2 = n)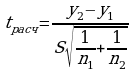 ,
,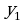 и
и 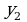 .
.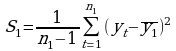 ;
; 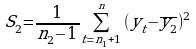 ;
;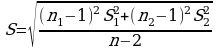 .
.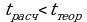 , гипотеза принимается
, гипотеза принимается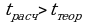 , гипотеза отвергается, тенденция развития есть.
, гипотеза отвергается, тенденция развития есть.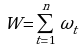 и
и 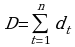 ,
,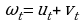 ,
,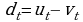 ,
,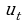 и
и 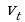 находят по формулам
находят по формулам 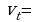
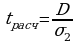 ,
,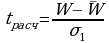 ,
,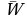 - среднее значение параметра W;
- среднее значение параметра W;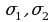 -среднеквадратичные ошибки W и D.(эти значения берутся из таблиц)
-среднеквадратичные ошибки W и D.(эти значения берутся из таблиц)









