Гомельская областная научно-практическая конференция учащихся
по естественно-научным и социально-гуманитарным направлениям
«Поиск»
Отдел образования Ельского райисполкома
ГУО «Движковский ясли-сад-базовая школа Ельского района»
Секция «Математика»
Методы решения нестандартныхуравнений в целых числах
Учебно-исследовательская работа
Выполнил
Свинтицкий Владислав Сергеевич, учащийся 9 класса
Руководитель
Черепанова Татьяна Михайловна, учитель математики
Движки, 2021
Оглавление
Введение 3
1. Уравнения в целых числах 4
2. Обзор методов 4
2.1. Группировка 4
2.2.Выделение полного квадрата 5
2.3. Оценка выражений, входящих в уравнение 5
2.4. Метод полного перебора всех возможных значений переменных, входящих в уравнение. 6
3. Решение в целых числах уравнения
9x2y2+6x2y2– 9x2y+2x2+y2– 18xy+7x – 5y+6=0 6
4. Решение в целых числах уравнения14x4– 5y4– 3x2y2+82y2– 125x2+51 = 0 8
5. Решение уравнения 2x2 + y2 + 7z2 + 2x2y2 - 42z + 33 = 0 10
6. Решение задачи. При каких x оба числа 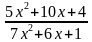 и
и 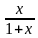 целые? 11
целые? 11
Заключение 14
Литература 15
Приложения…………………………………………………………………………16
1. Вспомогательное утверждение…………………………………………………16
2. Уравнения для самостоятельного решения……………………………………17
Введение
Каждый год в школе проводится математическая олимпиада. А олимпиадные задачи, как правило, являютсянестандартными,т. е. требующими использования знаний в нестандартных ситуациях.
Еще в древнегреческой математике, значительное место принадлежало сборникам математических развлечений и занимательным задачам. Прошли века, но интерес к занимательным математическим задачам не угас даже, наоборот, значение математики непрерывно возрастает. В математике рождаются новые идеи и методы. Все это расширяет сферу ее приложения. Сейчас уже нельзя назвать такой области деятельности людей, где математика не играла бы существенной роли. Она стала незаменимым орудием во всех науках о природе, в технике, в обществоведении. Даже юристы и историки берут на свое вооружениематематические методы.
Задача современногошкольника – эффективнорешать, как стандартные уравнения, решаемые по алгоритмам, так и уравнения, которые не являются стандартными. Такие уравнения требуют различных подходов к решению.
Уравнения, которые часто бывают весьма сложными и требующими нестандартного подхода к решению включаются в содержание олимпиад.
Актуальность работы состоит в том, что не всегда материалов, полученных на уроках достаточно, чтобы решать олимпиадные или конкурсные задания. Поэтому необходимы дополнительные сведения, которые позволят решать нестандартные задачи.
Какая же задача называется нестандартной? «Нестандартные задачи - это такие задачи, для которых в курсе математики не имеется общих правил и положений, определяющих точную программу их решения.» Однако, следует заметить, что понятие «нестандартная задача» является относительным. Одна и та же задача может быть стандартной или нестандартной, в зависимости от того, знакомы ли мы со способами решения задач такого типа. А многие задачи требуют и специальных знаний, подготовки. Конечно, для успешного решения любой задачи нужно уметь думать, догадываться, но этого мало. Полезно владеть и определенными общими подходами к решению таких задач. Поэтому я решил разобраться в решении уравнений высших степеней с несколькими неизвестными в целых числах, используя знания школьной программы, основанные на решении квадратных уравнений, попробовать их исследовать, найти общие подходы.
Целью данной работы является обобщение знаний о способах решения уравнений высших степеней с несколькими неизвестными в целых числах.
Для достижения поставленной цели в данной работе решались следующие задачи:
рассмотреть методы решения уравнений, основанные на использовании методов группировки и выделении полного квадрата, и сведения данного уравнения к решению квадратных уравнений;
применить на практике методы решения уравнений в целых числах.
наработать навыки в решении таких задач.
Объект исследования: уравнения высших степеней с несколькими неизвестными в целых числах.
Предмет исследования: применениеметодовгруппировки, выделения полного квадрата относительно одной из переменных, метода полного перебора значений переменных, оценка выражений, входящих в уравнение.
Гипотеза: не существует единого алгоритма, позволяющего за конечное число шагов решать в целых числах произвольные уравнения высших степеней. Но существует ряд нестандартных уравнений, задач, решения которых основываются на использовании методов группировки, выделения полного квадрата, методаполного перебора значений переменных, а также оценке выражений, входящих в уравнение. Указанные методы позволяют решать уравнения высших степеней с несколькими неизвестными в целых числах.
Уравнения в целых числах
Уравнения в целых числах– это алгебраические уравнения с двумя или более неизвестными переменными и целыми коэффициентами. Решениями такого уравнения являются все целочисленные (иногда натуральные или рациональные) наборы значений неизвестных переменных, удовлетворяющих этому уравнению. Такие уравнения ещё называют диофантовыми, в честь древнегреческого математика Диофанта Александрийского, который исследовал некоторые типы таких уравнений ещё до нашей эры.
Современной постановкой диофантовых задач мы обязаны французскому математику Ферма. Именно он поставил перед европейскими математиками вопрос о решении неопределённых уравнений только в целых числах. Наиболее известное уравнение в целых числах – великая теорема Ферма:
уравнение xn+ yn= zn не имеет ненулевых рациональных решений для всех натуральных n 2.
Теоретический интерес к уравнениям в целых числах достаточно велик, так как эти уравнения тесно связаны со многими проблемами теории чисел.
В 1970 году ленинградский математик Юрий Владимирович Матиясевич доказал, что общего способа, позволяющего за конечное число шагов решать в целых числах произвольные диофантовы уравнения, не существует и быть не может. Поэтому следует для разных типов уравнений выбирать собственные методы решения.
Обзор методов
2.1.Группировка
Группировку применяют в случае, когда многочлены не имеют общего множителя для всех членов многочлена. Объединение членов многочлена в группы можно осуществить различными способами. Не всегда группировка оказывается удачной. В таком случае следует попробовать объединить в группы другие члены многочлена.
2.2.Выделение полного квадрата
Выделение полного квадрата – это такое тождественное преобразование, при котором заданный трёхчлен представляется в виде суммы или разности квадрата двучлена и некоторого числового или буквенного выражения, т.е. основан на использовании формул:
a2+2ab+b2=(a+b)2;
a2−2ab+b2=(a−b)2.
Пример.
Найдите все целочисленные решения уравнения: х2 - 6ху + 13у2 = 29.
Решение:
Преобразуем левую часть уравнения, выделив полные квадраты:
х2 - 6ху + 13у2 = 29,
(х2 - 6ху + 9у2) + 4у2 = 29,
(х - 3у)2 + (2у)2 = 29,
значит (2у)2≤ 29.
Получаем, что у может быть равен 0; ±1, ±2.
у = 0, (х - 0)2 = 29. Не имеет решений в целых числах.
у = -1, (х + 3)2 + 4 = 29,
(х + 3)2 = 25,
х + 3 = 5 или х + 3 = -5,
х=2 х=-8.
у = 1, (х - 3)2 +4 =29,
(х - 3)2 =25,
х – 3 = 5 или х – 3 = -5,
х = 8 х = -2.
у = -2, (х + 6)2 + 16 = 29,
(х + 6)2 = 13. Нет решений в целых числах.
у=2, (х-6)2+16=29,
(х-6)2=13. Нет решений в целых числах.
Ответ: (2;-1); (-8;-1); (8;1); (-2;1)
2.3.Оценка выражений, входящих в уравнение
Решить в целых числах уравнение: (х2 + 4)(у2 + 1) = 8ху
Решение: Заметим, что если (х;у ) – решение уравнения, то (-х ;-у ) – тоже решение. И так как х = 0 и у = 0 не являются решением уравнения, то, разделив обе части уравнения на ху, получим: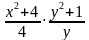 = 8, (х+
= 8, (х+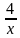 )(у +
)(у +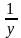 ) = 8.
) = 8.
Пусть х0, у0, тогда, согласно неравенству Коши, х+ 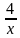 ≥ 2
≥ 2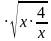 = 4,
= 4,
у + 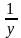 ≥ 2
≥ 2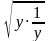 = 2, тогда их произведение (х+
= 2, тогда их произведение (х+ 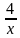 )(у +
)(у + 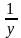 ) = 4·2 = 8,
) = 4·2 = 8,
значит, х+ 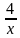 = 4 и у +
= 4 и у + 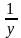 = 2.
= 2.
Отсюда находим х=2 и у=1 – решение, тогда х = -2 и у = -1 – тоже решение.
Ответ: (2;1); (-2;-1)
2.4. Метод полного перебора всех возможных значений переменных, входящих в уравнение.
Пример.
Найти множество всех пар натуральных чисел, которые являются решениями уравнения 49х + 51у = 602.
Решение: Выразим из уравнения переменную х через у.
х= 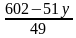 , так как х и у – натуральные числа, то х = 602 - 51у ≥ 49, 51у≤553, 1≤у≤10 .
, так как х и у – натуральные числа, то х = 602 - 51у ≥ 49, 51у≤553, 1≤у≤10 .
Полный перебор вариантов показывает, что натуральными решениями уравнения являются х=5, у=7.
Ответ: (5;7).
Решение в целых числах уравнения
9
x2y2+6
x2y2– 9
x2y+2
x2+
y2– 18
xy+7
x – 5
y+6=0
Сгруппируем так слагаемые, чтобы можно было получить квадратное уравнение относительно одной из переменной x или y. Таким образом получим квадратное уравнение относительно y:
9x2y2 + 6x2y2 + y2 – 9x2y – 18xy - 5y + 2x2+7x + 6 = 0,
(9x2 + 6x2 + 1)y2 – (9x2 +18x + 5)y + (2x2+7x + 6) = 0, здесь легко заметить, что коэффициент при y2 – это полный квадрат (3x + 1)2. Разложив на линейные множители коэффициент при y и свободный коэффициент, получим следующее уравнение:
(3x + 1)2·y2 – (3x + 1)(3x + 5)y + (2x + 3)(x + 2) = 0.
Если решать это уравнение через дискриминант и формулы корней, то будем иметь громоздкие вычисления, но можно привести его к виду приведенного квадратного уравнения. Для этого надо разделить почленно на (3x+1)2. Это выражение заведомо ≠0, так как 3x+1=0 при x=-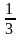 , что невозможно, так как мы решаем уравнение в целых числах.
, что невозможно, так как мы решаем уравнение в целых числах.
y2 – 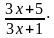 y +
y + 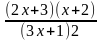 = 0, не сложно заметить, что сумма множителей, стоящих в числителе свободного коэффициента равна числителю коэффициента при y. Перепишем уравнение в виде:
= 0, не сложно заметить, что сумма множителей, стоящих в числителе свободного коэффициента равна числителю коэффициента при y. Перепишем уравнение в виде:
y2 – 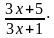 y +
y + 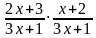 = 0, это наблюдение даёт возможность применить теорему Виета:
= 0, это наблюдение даёт возможность применить теорему Виета:
y1 · y2= 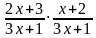 ,
,
y1 + y2 = – 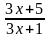 .
.
y1= 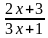 , y2 =
, y2 = 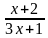 .
.
Имеем два решения y1 и y2, которые надо оценить, чтобы найти целые значения.
Оценим y1= 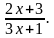 Разделим числитель на знаменатель, это можно выполнить уголком, получим:
Разделим числитель на знаменатель, это можно выполнить уголком, получим:
y1= 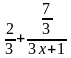 ;
;
3·y1 = 2 +  , очевидно, что левая часть принадлежит Z, 2 – целое число, значит дробь
, очевидно, что левая часть принадлежит Z, 2 – целое число, значит дробь  должна принадлежать множеству Z. Оценить это выражение не сложно: возможные целые значения равны ±7, ±1. Рассмотрим все случаи.
должна принадлежать множеству Z. Оценить это выражение не сложно: возможные целые значения равны ±7, ±1. Рассмотрим все случаи.
3x+1=-1, x=  , решений в целых числах нет.
, решений в целых числах нет.
3x+1= 1, x = 0.
Найдём y: 3·y1 = 2 +  ,
,
3·y1 = 2 + 7,
3·y1 = 9,
y1 = 3.
Имеем решение (0; 3).
3x+1=-7, x=  , решений в целых числах нет.
, решений в целых числах нет.
3x+1= 7, x = 2.
Найдём y: 3·y1 = 2 +  ,
,
3·y1 = 3,
y1 = 1.Имеем решение (2; 1).
Аналогично оценим y2 =  Разделим числитель на знаменатель, это можно выполнить уголком, получим: y2=
Разделим числитель на знаменатель, это можно выполнить уголком, получим: y2=  ;
;
3·y2 = 1 +  , очевидно, что левая часть принадлежит Z, 1 – целое число, значит дробь
, очевидно, что левая часть принадлежит Z, 1 – целое число, значит дробь  должна принадлежать множеству Z. Оценить это выражение не сложно: возможные целые значения равны ±5, ±1. Рассмотрим все случаи.
должна принадлежать множеству Z. Оценить это выражение не сложно: возможные целые значения равны ±5, ±1. Рассмотрим все случаи.
3x+1=-1, x=  , решений в целых числах нет.
, решений в целых числах нет.
3x+1= 1, x = 0.
Найдём y: 3·y2 = 1 +  ,
,
3·y2 = 1 + 5,
3·y2 = 6,
y2 = 2.
Имеем решение (0; 2).
3x+1= 5, x=  , решений в целых числах нет.
, решений в целых числах нет.
3x+1= -5, x = -2.
Найдём y: 3·y2 = 1 +  ,
,
3·y2 = 1 - 1,
y2 = 0.
Имеем решение (-2; 0).
Ответ: (0; 3), (2; 1), (0; 2), (-2; 0).
Вывод: были применены метод группировки и решение уравнения относительно одной из переменных (y), метод полного перебора возможных значений переменных, входящих в уравнение.
4. Решение в целых числах уравнения 14
x4– 5
y4– 3
x2y2+82
y2– 125
x2+51 = 0
Замечаем, что переменные входят в уравнение симметрично: x2, x4, y2, y4 – это значит, изменение знака этих переменных ни на что не повлияет. Это значит, если пара (x; y) – решение уравнения, то и (x; -y), (-x; y), (-x; -y) будут являться решениями. Также очевидно, что переменные не могут одновременно быть равными 0.
Запишем биквадратное уравнение относительно x (можно было бы записать относительно y, возможно какой-то из вариантов окажется проще).
14x4 – 3x2y2 – 125x2 –5y4 + 82y2 + 51 = 0,
14x4 – (3y2 + 125)x2 – (5y4 – 82y2 – 51) = 0, если решать стандартным способом, то дискриминант получится достаточно сложным. Как и в решении уравнения пункта 3, попробуем применить теорему Виета, разделив для этого обе части уравнения на 14, а свободный коэффициент разложим на линейные множители:
x4 –  ·x2 – = 0, по т.Виета
·x2 – = 0, по т.Виета
x12 + x22 =  ,
,
x12 · x22 = .
Подбираем корни: x12 =  , x22=
, x22=  – решения биквадратного уравнения. Решим каждое из уравнений в целых числах.
– решения биквадратного уравнения. Решим каждое из уравнений в целых числах.
Решим уравнение 2x12 = –y2+ 17,
2x12 + y2 = 17, очевидно, что
Рассмотрим возможные случаи:
x: 0; ±1; ±2.
y: 0; ±1; ±2; ±3; ±4.
Можно оценивать не x, а x2:
x2 = 1, то y = 15, нет решений в целых числах.
x2 = 4, то y2 = 9, y = ± 3.
Имеем пары целочисленных решений уравнения 2x12 = – y2 + 17:
(2; 3), (2; -3), (-2; 3), (-2; -3).
Решим уравнение:7x22 = 5y2 + 3.
7x22 - 5y2 = 3.
Применим вспомогательное утверждение: если x∈Z, то либо x2 делится на 3, либо x2+1 делится на 3 (доказательство приведено в приложении 1).
Рассмотрим случаи:
Пусть тогда уравнение 7x22 - 5y2 = 3 примет вид:
7·9p2 - 5·9q2 = 3,
7·3p2 - 5·3q2 = 1,
3(7p2 - 5q2) = 1, очевидно, что левая часть делится на 3, правая часть на 3 не делится. Значит в целых числах это уравнение решений не имеет.
Пусть тогда, согласно вспомогательного утверждения, следует, что y2–1 делится на 3. Уравнение 7x22 - 5y2 = 3 примет вид:
7·9p2 - 5(y2–1) = 3+5, (добавили 5 к обеим частям).
7·9p2 - 5(y2–1) = 8, - очевидно, что левая часть делится на 3, а правая – нет. Значит в целых числах это уравнение решений не имеет.
Пусть тогда, согласно вспомогательного утверждения, следует, что x2–1 делится на 3. Уравнение 7x22 - 5y2 = 3 примет вид:
7(x2-1)2 - 5y2 = 3 – 7, (вычли 7 из обеих частей)
7(x2-1)2 - 5y2 = – 4, очевидно, что левая часть делится на 3, а правая – нет. Значит в целых числах это уравнение решений не имеет.
Пусть тогда, согласно вспомогательного утверждения, следует, что x2–1 делится на 3 и y2–1 делится на 3. Уравнение 7x22 - 5y2 = 3 примет вид:
7(x22-1)– 5(y2-1) = 3 – 7 + 5, (вычли 7 из обеих частей, добавили 5 к обеим частям)
7(x22-1)– 5(y2-1) = 1, очевидно, что левая часть делится на 3, а правая – нет. Значит в целых числах это уравнение решений не имеет.
Таким образом уравнение 7x22 - 5y2 = 3 решений в целых числах не имеет, значит решения уравнения 2x12+y2 = 17 являются решением исходного уравнения 14x4 – 5y4 - 3x2y2 + 82y2 – 125x2 + 51 = 0.
Ответ: (2; 3), (2; -3), (-2; 3), (-2; -3).
Вывод: были применены метод группировки и решение уравнения относительно одной из переменных (x), метод полного перебора возможных значений переменных, входящих в уравнение.
5. Решение уравнения 2
x2 +
y2 + 7
z2 + 2
x2y2 - 42
z + 33 = 0
Применим метод выделения полного квадрата относительно переменной z. Представляем слагаемое -42z, как удвоенное произведение, замечаем, что оно кратно 7, так же, как и слагаемое 7z2, что позволяет вынести 7 за скобки, тогда 6z=2·z·3 будем рассматривать как удвоенное произведение, добавляем и тут же вычитаем 7·32=63:
2x2 + y2 + (7z2 - 42z + 63) – 63 + 2x2y2 + 33 = 0,
2x2 + y2 + 7(z2 - 6z + 9) – 63 + 2x2y2 + 33 = 0,
2x2 + y2 + 7(z-3)2– 63 + 2x2y2 + 33 = 0,
2x2 + y2 + 7(z-3)2 – 30 + 2x2y2 = 0,
2x2 + y2 + 7(z-3)2 + 2x2y2 = 30.
Замечаем, что сумма 4-х целых, неотрицательных слагаемых равна 30.
Чтобы минимизировать количество вариантов выполним группировку:
(2x2y2 + 2x2) + (y2 + 1) – 1 + 7(z-3)2 = 30,
2x2 (y2 + 1) + (y2 + 1) + 7(z-3)2 = 30 + 1,
(2x2 + 1) (y2 + 1) + 7(z-3)2 = 31.
Переходим к оценке выражений, входящих в уравнение. Относительно выражения 7(z-3)2 делаем вывод, что 7(z-3)2 ≤ 31. Возможны следующие варианты:
7·0 ≤ 31; 7·1 ≤ 31; 7·2 ≤ 31; 7·3 ≤ 31; 7·4 ≤ 31; 7·5 ≥ 31.
Если (z-3)2 = 0, значит (2x2 + 1)(y2 + 1) = 31 = 1·31=31·1.
2x2 + 1 =1 и y2 + 1= 31,
2x2 = 0 y2 = 30 – решений в целых числах нет.
x = 0.
2x2 + 1 =31 и y2 + 1 = 1,
2x2 = 30 y2 = 0.
x2 = 15 – решений в целых числах нет.
Если (z-3)2 = 1, значит (2x2 + 1)(y2 + 1) + 7·1 = 31,
(2x2 + 1)(y2 + 1) = 24.
Замечаем, множитель (2x2 + 1) нечётный, тогда имеем:
(2x2 + 1) (y2 + 1) = 24=1·24=3·8.
2x2 + 1 = 1 и y2 + 1= 24,
2x2 = 0 y2 = 23 – решений в целых числах нет.
x = 0.
2x2 + 1 = 3 и y2 + 1 = 8,
2x2 = 2 y2 = 7– решений в целых числах нет.
x2 = 1
x = ± 1.
Если (z-3)2 = 2, то решений в целых числах нет, т.к. z-3≠ .
.
Если (z-3)2 = 3, то решений в целых числах нет, т.к. z-3≠ .
.
Если (z-3)2 = 4, значит (2x2 + 1) (y2 + 1) + 7·4 = 31,
(2x2 + 1) (y2 + 1) = 3 = 1·3 = 3·1.
2x2 + 1 = 1 и y2 + 1= 3,
x = 0y2 = 2 – решений в целых числах нет.
2x2 + 1 = 3 и y2 + 1 = 1,
x = ± 1 y= 0.
Найдём переменную z.
= =
Таким образом имеем следующие тройки решений:
(1;0;1), (1;0;5), (-1;0;1), (-1;0;5).
Ответ: (1;0;1), (1;0;5), (-1;0;1), (-1;0;5).
Вывод: были применены метод выделения полного квадрата относительно переменной z, метод оценки выражений, входящих в уравнение, метод полного перебора возможных значений переменных, входящих в уравнение.
6. Решение задачи. При каких
x оба числа
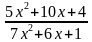
и
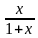
целые?
Введём замену. Пусть M=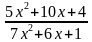 и N=
и N= Из более простого выражения выразим x через y:
Из более простого выражения выразим x через y:
N=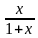 ,
,
N · (1+x) = x,
N + N·x = x,
x – N·x = N,
x·(1 – N) = N, 1 – N ≠ 0,
x=  , подставим в уравнение M:
, подставим в уравнение M:
M =
M =
M =  выполним деление числителя на знаменатель, получим:
выполним деление числителя на знаменатель, получим:
M =  +
+
2M= ,
2M + 1 = , замечаем, что число, стоящее в левой части принадлежит множеству Z, значит и число правой части должно быть целым. В правой части степень знаменателя степени числителя, значит при больших значениях N дробь стремится к 0. Делаем вывод, что слишком большими значения N не будут. Рассматриваемая дробь будет принимать целые значения при выполнении следующих условий:

≥ 1,
≥ -1,

≤ 0,
≤ 0,

 ≤ 0,
≤ 0,
≤ 0,

≤ 0,
≤ 0,
Проанализируем каждое из полученных решений.
Оценим первое неравенство, для начала упорядочим полученные числа:
-1- ; 1-
; 1- ; -1+
; -1+ ; 1+
; 1+ ;
;
-
 2; -1-
2; -1- ; 1-
; 1- ;-1; -1+
;-1; -1+ ; 0; 1; 2; 3; 1+
; 0; 1; 2; 3; 1+ ; 4.
; 4.

 ● ○ ● ● ○ ● ● ● ● ● ●
● ○ ● ● ○ ● ● ● ● ● ●
-2 -1- 1-
1- -1 -1+
-1 -1+ 0 1 2 3 1+
0 1 2 3 1+ 4
4
N∈ (1- ; 1-
; 1- ] ∪ (-1+
] ∪ (-1+  ; 1+
; 1+ ]. Так как нам нужны целые значения N, то
]. Так как нам нужны целые значения N, то
N = {0; 1; 2; 3}.
Вернёмся к уравнению 2M + 1 = , оценим каждое решение N.
N = 0, 2M + 1 =  ,
,
2M + 1 =  ,
,
2M=  ,
,
M = 4, так как получили целые числа, то есть решение.
N=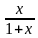 ⇒x = 0 – решение задачи.
⇒x = 0 – решение задачи.
N = 1, 2M + 1 =  ,
,
2M + 1 =  , решений в целых числах нет.
, решений в целых числах нет.
N = 2, 2M + 1 =  , решений в целых числах нет.
, решений в целых числах нет.
N = 3, 2M + 1 =  , решений в целых числах нет.
, решений в целых числах нет.
Имеем одно решение: при x = 0, N = 0.
Оценим второе неравенство ≤ 0, для этого упорядочим полученные числа:
-5; -1- ; -1; -1+
; -1; -1+ ;
;
-
 5; -4; -3; -2; -1-
5; -4; -3; -2; -1- ; -1; -1+
; -1; -1+ .
.

 ● ● ● ● ○ ● ○
● ● ● ● ○ ● ○
-5 -4 -3 -2 -1-  -1 -1+
-1 -1+
N∈ [-5; -1- ) ∪ [-1; -1+
) ∪ [-1; -1+ ).
).
Так как нам нужны целые значения N, то N = {-5; -4; -3; -2; -1}.
Вернёмся к уравнению 2M + 1 = , оценим каждое решение N.
N = -5, 2M + 1 = ,
2M + 1 = -1,
M = -1, так как получили целые числа, то есть решение.
N=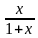 ⇒-5=
⇒-5=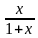 ⇒x =
⇒x =  – решение задачи.
– решение задачи.
N = -1, 2M + 1 = ,
2M + 1 = -1,
M = -1, так как получили целые числа, то есть решение.
N=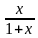 ⇒-1=
⇒-1=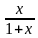 ⇒x =
⇒x =  – решение задачи.
– решение задачи.
N = -4, 2M + 1 =  , решений в целых числах нет.
, решений в целых числах нет.
N = -3, 2M + 1 =  , решений в целых числах нет.
, решений в целых числах нет.
N = -2, 2M + 1 = ,
2M + 1 = -7,
M = -4, так как получили целые числа, то есть решение.
N=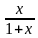 ⇒-2=
⇒-2=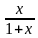 ⇒x =
⇒x =  – решение задачи.
– решение задачи.
Ответ: при x = 0, x=  ,x =
,x =  , x =
, x =  .
.
Вывод: были применены метод оценки выражений, входящих в уравнение, метод полного перебора возможных значений переменных, входящих в уравнение. Задачи для самостоятельного решения представлены в приложении 2.
Заключение
При выполнении работы была изучена и проанализирована научно-популярная и учебная литература по указанной теме, в том числе и примеры решений уравнений в целых числах из математической олимпиады для школьников, из математических олимпиад. Опираясь на информацию, полученную после изучения литературы и анализа решения уравнений были сделаны следующие выводы:
рассмотренные уравнения встречаются в олимпиадах, в различных конкурсах, развивая логическое мышление, повышая уровень математической культуры, прививая навыки самостоятельной исследовательской работы в математике;
при решении рассмотренных уравнений в целых числах были примененытакие методы как оценка выражений, входящих в уравнение, выражение одной переменной через другую и выделение целой части дроби, метод полного перебора всех возможных значений переменных, входящих в уравнение, метод, основанный на выделении полного квадрата, метод решения уравнений с двумя переменными, как квадратных относительно одной из переменных.
Таким образом, выдвинутая гипотеза исследования о том, что не существует единого алгоритма, позволяющего за конечное число шагов решать в целых числах нестандартные уравнения высших степеней нашла свое подтверждение. Проведенное исследование также показало, что используя знания школьной программы, факультативных курсов, логическое мышление, можно решить ряд нестандартных задач, уравнений в целых числах.
Этот материал может быть интересен и полезен учителям и учащимся, готовящимся к олимпиадам, математическим конкурсам,а также учащимся для самостоятельного изучения.
Любое задание должно чему-нибудь научить. Решение каждой задачи должно быть шагом вперед в развитии математических знаний, умений и навыков, должно обогащать знания и опыт, учить ориентироваться в различных ситуациях.
Литература
Фридман, Л. М.Как научиться решать задачи : пособие для учащихся /Л. М. Фридман, Е.Н. Турецкий. — М.: Просвещение, 1984.— 175 с.
Иванов, О. А. Практикум по элементарной математике. Алгеброаналитические методы /О. А. Иванов. — М.: МЦНМО, 2001. — 320 с.
Морозова, Е. А. Международные математические олимпиады /Е. А. Морозова. —М.: Просвещение, 1976. —288 с.
Приложение 1
Вспомогательное утверждение
Вспомогательное утверждение: если x∈Z, то либо x2 делится на 3, либо x2-1 делится на 3.
Доказательство.
Любое число можно представить в виде:
2n – чётное число, (2n+1) – нечётное число. Здесь удобнее рассматривать как числа при делении на 2, дающие остаток 0 (числа 2n), дающие остаток 1 (числа 2n+1). Все числа можем представить следующим образом:
3n – числа при делении на 3 с остатком 0;
3n + 1 – числа при делении на 3 дают остаток 1;
3n + 2 – числа при делении на 3 дают остаток 2.
Аналогично можно представить все целые числа при делении на 4, на 5 и т.д.
Рассмотрим числа 3n, 3n + 1, 3n + 2.
Если x=3n, то x2= 9n2 – делится на 3.
Если x=3n+1, то x2= (3n+1)2= 9n2 + 6n + 1= 3(3n+2) +1 – не делится на 3. Посмотрим, как ведет себя (x-1)2 = (x-1)(x+1) = 3n(3n+2) – делится на 3.
Если x=3n+2, то x2= (3n+2)2= 9n2 + 12n + 4 = 9n2 + 12n + 3 + 1 = 3(3n2 + 4n + 1) + 1 – не делится на 3. Посмотрим, как ведет себя (x-1)2 = (x-1)(x+1) = (3n+1) (3n+3) = 3(3n+1) (n+1) – делится на 3.
Доказано.
Приложение 2
Уравнения для самостоятельного решения
Найти все целочисленные решения уравнения
10x4 – 2y4 + x2y2 + 29y2 – 113x2 + 171 = 0.
Найти все тройки целых чисел (p; q; s), для которых выполняется равенство 4p2 + 3q2 + 5s2 – 24q – 1 = 0.
При каких x оба числа и являются целыми?
являются целыми?







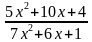 и
и 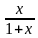 целые? 11
целые? 11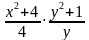 = 8, (х+
= 8, (х+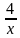 )(у +
)(у +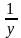 ) = 8.
) = 8. 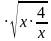 = 4,
= 4, 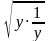 = 2, тогда их произведение (х+
= 2, тогда их произведение (х+ 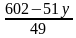 , так как х и у – натуральные числа, то х = 602 - 51у ≥ 49, 51у≤553, 1≤у≤10 .
, так как х и у – натуральные числа, то х = 602 - 51у ≥ 49, 51у≤553, 1≤у≤10 . 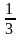 , что невозможно, так как мы решаем уравнение в целых числах.
, что невозможно, так как мы решаем уравнение в целых числах.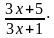 y +
y + 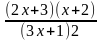 = 0, не сложно заметить, что сумма множителей, стоящих в числителе свободного коэффициента равна числителю коэффициента при y. Перепишем уравнение в виде:
= 0, не сложно заметить, что сумма множителей, стоящих в числителе свободного коэффициента равна числителю коэффициента при y. Перепишем уравнение в виде: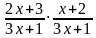 = 0, это наблюдение даёт возможность применить теорему Виета:
= 0, это наблюдение даёт возможность применить теорему Виета: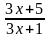 .
.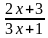 , y2 =
, y2 = 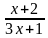 .
.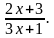 Разделим числитель на знаменатель, это можно выполнить уголком, получим:
Разделим числитель на знаменатель, это можно выполнить уголком, получим: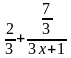 ;
;

















