Нестандартные способы решения квадратных уравнений

Муниципальное казенное общеобразовательное учреждение

«Богучарская средняя общеобразовательная школа №1»

Научно-исследовательская работа по теме: «Нестандартные способы решения квадратных уравнений»

Автор: ученица 9«А» класса

Прядкова Екатерина Сергеевна

Руководитель: Алабина Галина Юрьевна

Выявить способы решения квадратных уравнений

Узнать можно ли решить любое квадратное уравнение данными способами и выделить особенности и недостатки этих способов

• Анализировать источники литературы для выявления способов решения квадратных уравнений
• Показать различные способы решения квадратных уравнений
• Выявить наиболее удобные способы решения квадратных уравнений
• Научиться решать квадратные уравнения различными способами

Существуют другие способы решения квадратного уравнения кроме тех, которые мы изучили в школе

Способы решения квадратных уравнений

Разложение левой части на множители

Метод выделения полного квадрата

По формуле

Основные

С использованием теоремы Виета (прямой и обратной)

Графический способ

По свойствам коэффициентов

Способом «переброски»

Дополнительные

С помощью циркуля и линейки

С помощью номограммы

Геометрический способ

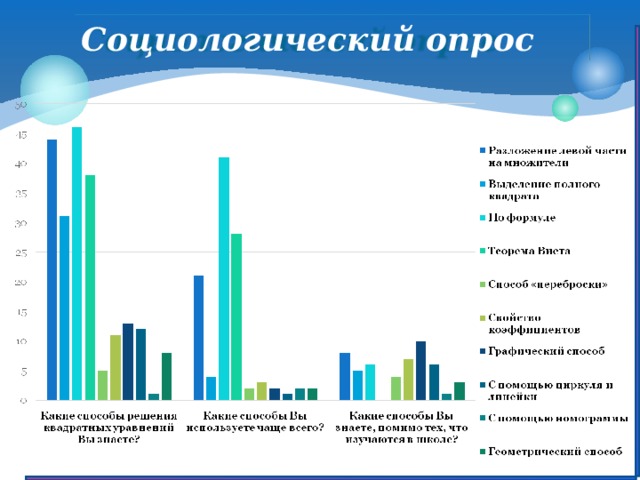
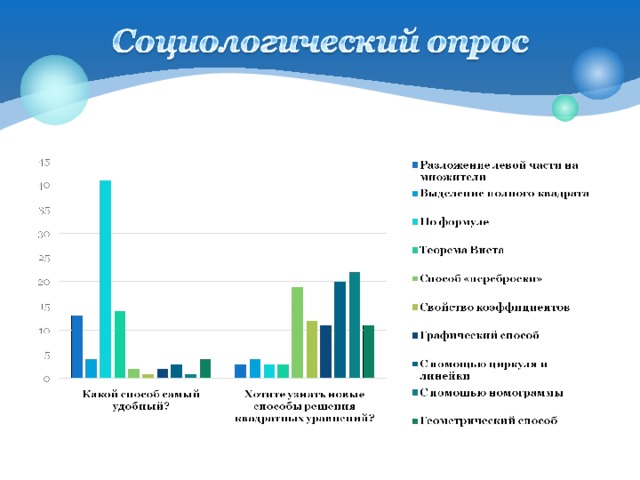
Социологический опрос

Свойства коэффициентов

Свойства:

Способ «переброски»

Умножив обе части уравнения на а, получим

Пусть

, откуда

Тогда получим уравнение с новой переменной

Его корни у 1 и у 2 . Окончательно

С помощью циркуля и линейки

Радиус окружности больше ординаты центра

, окружность пересекает ось Ох в двух точках , где корни исходного уравнения.

Радиус окружности равен ординате центра

, окружность пересекает ось Ох в одной точке где корень исходного уравнения.

Радиус окружности меньше ординаты центра

, окружность не имеет общих точек с осью Ох. В этом случае исходное уравнение не имеет корней.

С помощью номограммы

х 2 -9х+8=0

Х 1 =8; х 2 =1

Геометрический способ

Рассмотрим, как древние греки решали уравнение

Решение представлено на рисунке, где

или

Выражения

и 16 + 9

геометрически представляют собой один и тот же квадрат со стороной 5.

Поэтому

Обработка данных

Метод выделения

полного квадрата

Разложение левой части

уравнения на множители

Ответ: -4,5; 1.

Обработка данных

С использованием

формул Виета

По формуле

имеет два разных

по знаку корня

больший по модулю

корень отрицательный

Ответ: -4,5; 1.

Обработка данных

По свойству коэффициентов

Способом «переброски»

Перебросим коэффициент а = 2 к свободному члену и получим уравнение:

Так как

то

из которого по формулам Виета

Корнями исходного уравнения будут

Ответ: -4,5; 1.

Обработка данных

Графический метод

С помощью циркуля и линейки

Запишем уравнение в виде

Определим координаты центра окружности по формулам:

Построим в одной системе координат графики функций

Проведем окружность радиуса SA, где А (0;1).

Ответ: -4,5; 1.

Обработка данных

Геометрический способ

С помощью номограммы

Представим уравнение в виде:

Представим уравнение в виде:

Площадь полученного квадрата:

Так как

Номограмма дает положительный корень

то:

Таким образом, получили уравнение:

отрицательный корень

Ответ: -4,5; 1.

Положительные стороны и недостатки

Название способа решения квадратных уравнений

Положительные стороны

Разложение левой части уравнения на множители

Недостатки

Дает возможность сразу увидеть корни уравнения.

Метод выделения полного квадрата

Нужно правильно расчленить слагаемые для

группировки.

По формуле

За минимальное количество действий можно найти корни уравнений

Нужно правильно найти все слагаемые для выделения полного квадрата.

Можно применить ко всем квадратным уравнениям.

С использованием формул Виета

Нужно выучить формулы.

Достаточно легкий способ, дает возможность сразу увидеть корни уравнения.

Легко находятся только целые корни.

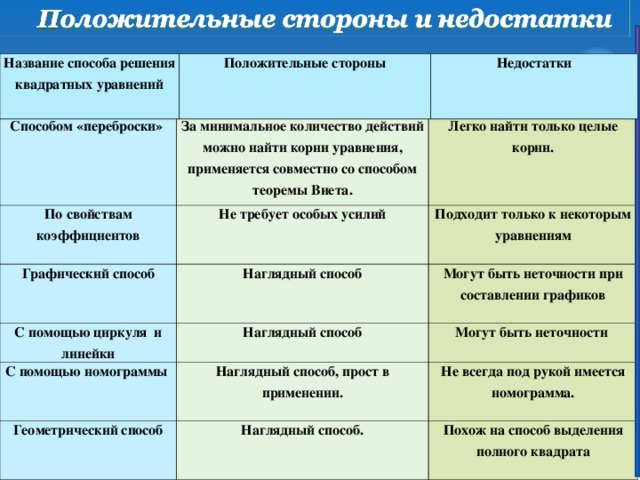
Название способа решения квадратных уравнений

Положительные стороны

Недостатки

Способом «переброски»

За минимальное количество действий можно найти корни уравнения, применяется совместно со способом теоремы Виета.

По свойствам коэффициентов

Графический способ

Легко найти только целые корни.

Не требует особых усилий

Наглядный способ

Подходит только к некоторым уравнениям

С помощью циркуля и линейки

Могут быть неточности при составлении графиков

Наглядный способ

С помощью номограммы

Наглядный способ, прост в применении.

Могут быть неточности

Геометрический способ

Наглядный способ.

Не всегда под рукой имеется номограмма.

Похож на способ выделения полного квадрата

Для того, чтобы хорошо решать любое квадратные уравнения необходимо

знать:

    формулу нахождения дискриминанта;

    формулу нахождения корней квадратного уравнения;

    алгоритмы решения уравнений данного вида.

уметь:

    решать неполные квадратные уравнения;

    решать полные квадратные уравнения;

   решать приведенные квадратные уравнения;

  находить ошибки в решенных уравнениях и исправлять их;

    делать проверку.

Думаю, что моя работа будет интересна учащимся 8-9 классов, а также тем, которые хотят научиться рационально решать квадратные уравнения и хорошо подготовиться к выпускным экзаменам. На уроках математики я рассказала своим одноклассникам методы решения квадратных уравнений и ребятам они понравились. Также она будет интересна и учителям математики, так как в своей работе я не только рассмотрела методы решения квадратных уравнений, но и историю их развития.