К ыргыз республикасы билим бер\\ министирлиги
ыргыз республикасы билим бер\\ министирлиги

Тема: «Метрикалык мейкиндик»
Даярдаган:Нишанбаева Назг\л
Группа: МК(м)-1-19
План:
1.Кириш\\
2.Метрикалык мейкиндик т\ш\н\г\
3. Метрикалык мейкиндиктин т\рлър\ жана ъзгъчъл\ктър\
4.Метрикалык мейкиндикке карата мисалдар.
5.Метрикалык мейкиндиктин колдонулушу
6. Кортунду
7. Колдонуган адабияттар
1.Кириш\\
Баарына белгил\\ болгондой эле математика илиминде “ аралык” т\ш\н\г\ кеёири колдонулган жана изилденип келе жаткан т\ш\н\к. Бул “аралык” т\ш\н\г\ аналитикалык геометрияда Евклидик мейкиндиктеги геометриялык объектердин касиеттерин изилдъъ \ч\н колдонулуп келе жатат. Ал эми математикалык анализде сан удаалаштыгынын чеги катарындагы фундаменталдык т\ш\н\к катары каралат. Аралык тууралуу белгил\\ болгон т\ш\н\ктърд\ жалпылап француз математиги М. Фреше 1906-жылы илимге метрикалык мейкиндик т\ш\н\г\н киргизген.
Бул иште ушул метрикалык мейкиндик т\ш\н\г\ жана ага карата мисалдар, мисалдардын чыгарылыштары каралат.
2.Метрикалык мейкиндик т\ш\н\г\
Метрика –бул берилген мейкиндиктеги каалаган эки чекиттин арасындагы аралыкты аныктоочу формула же эреже.
Аныктама 1: Метрикалык мейкиндик деп Х къпт\г\нън жана d: Х×Х → R аралык функциясынан (метрикадан) т\з\лгън ошону менен бирге тъмънк\ аксиомаларды канаатандыруучу (Х, d) жубтугун айтабыз:
М1. d(x, y) ≥0, 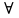 x , y
x , y ; (терс эместик аксиомсы)
; (терс эместик аксиомсы)
М2. d(x, y) = 0, x = y; (теёдештик аксиомасы)
М3. d(x, y) = d(y, x); (симметриялуулук аксиомасы);
М4. d(x, z) ≤ d(x, y) + d(y, z) ; (уч бурчтуктун жактарына карата аксиомасы же уч буртук барабарсыздыгы).
Эскерт\\:
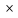


Аныктама 2: Метрикалык мейкиндик деп ъз\ндъг\ метрика менен бирге берилген X къпт\г\н айтабыз, ал эми x, y, z,... X элементтери метрикалык мейкиндиктин чекиттери деп аталат.
X элементтери метрикалык мейкиндиктин чекиттери деп аталат.
Эскерт\\:
Аныктама: Х метрикалык мейкиндигинде берилген d1 (x, y) жана d2 (x, y) метрикалары эквивалентт\\ болушат.
3.Метрикалык мейкиндиктин т\рлър\ ъзгъчъл\ктър\
1.Х къпт\г\ 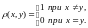 метрикасы менен метрикалык мейкиндик болот жана ал дискреттикит (\зг\лт\кт\\) мейкиндик деп аталат.
метрикасы менен метрикалык мейкиндик болот жана ал дискреттикит (\зг\лт\кт\\) мейкиндик деп аталат.
Далилдейбиз:
1.  аткарылат.
аткарылат.
2.  аткарылат
аткарылат
3. 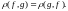 аткарылат
аткарылат
/ч бурчтук барабарсыздыгы жън\ндъг\ аксиоманын аткарылышын текшеребиз.

 Анда
Анда  жана
жана 
 Жыйынтыгында баардык х \ч\н тъмънк\н\ алабыз:
Жыйынтыгында баардык х \ч\н тъмънк\н\ алабыз:

Ошондуктан 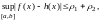 башкача айтканда
башкача айтканда 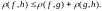
Демек \ч бурчтук барабарсыздыгы аксиомасы аткарылат.



Мында  R
R
Аныктама. R чыныгы сандар С комплекстик сандар талаасына
 сызыктуу мейкиндиги нормаланган мейкиндик деп аталат. Мында ар бир
сызыктуу мейкиндиги нормаланган мейкиндик деп аталат. Мында ар бир
 вектору
вектору  анык санын чагылдырат, тъмънк\ аксиомаларды канаатандырат:
анык санын чагылдырат, тъмънк\ аксиомаларды канаатандырат:
(Н1) 

(Н2) каалаган  жана каалаган
жана каалаган  R (же С)
R (же С) 
(Н3) калаган  \ч\н
\ч\н 
 метрикасы менен аныкталган нормаланган мейкиндик метрикалык мейкиндик деп аталат.
метрикасы менен аныкталган нормаланган мейкиндик метрикалык мейкиндик деп аталат.
(М1)-(М4)- аксиомаларын канаатандырган мейкиндиктер (Н1)-(Н3) аксиомаларын да канаатандырышат. Ошондуктан жогоруда мисал келтирилген 2,3,4,5,6,7 мейкиндиктер нормаланган мейкиндик боло алышат. Дискреттик мейкиндик нормаланган мейкиндик болбойт. 6- мисалдагы  формулаларын тъмънк\дъй кър\н\штъ жазууга болот:
формулаларын тъмънк\дъй кър\н\штъ жазууга болот:



Эскерт\\. 1) С n-ълчъмд\\ комплекстик сызыктуу мейкиндикти да нормаланган мейкиндик катары кароого болот мындан метрикалык мейкиндик экендиги келип чыгат. Мында норма тъмънк\ формула менен аныкталат
n-ълчъмд\\ комплекстик сызыктуу мейкиндикти да нормаланган мейкиндик катары кароого болот мындан метрикалык мейкиндик экендиги келип чыгат. Мында норма тъмънк\ формула менен аныкталат

мында  С
С ал эми
ал эми  С.
С.
4.Метрикалык мейкиндикке карата мисалдар
(Х,d) метрикалык мейкиндигинде d(x,y) функциясы метрика болоорун текшергиле. Ал \ч\н ар бир функциянын метрикалык мейкиндиктин акциомаларын канаатандыраарын текшеребиз.
№1- мисал:
 функциясын текшеребиз.
функциясын текшеребиз.
d(x, y) ≥0, 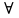 x , y
x , y ; (терс эместик акциомсы)
; (терс эместик акциомсы)
бул акциома аныктамага ылайык аткарылышына шек жок.
d(x, y) = 0, x = y; (теёдештик акциомасы)
бул акциоманы текшерип къръб\з
 =
= демек аткарылат.
демек аткарылат.
d(x, y) = d(y, x); (симметриялуулук акциомасы);
 жана
жана 
 ,
,
Мисалга алсак 

 демек бул акциома аткарылбайт.
демек бул акциома аткарылбайт.
d(x, z) ≤ d(x, y) + d(y, z) ; (уч бурчтуктун жактарына карата акциомасы же уч бурчтук барабарсыздыгы )
 функциясы \ч\н бул акциоманы текшериштин кажети жок.
функциясы \ч\н бул акциоманы текшериштин кажети жок.
Демек  функциясы метрика болбойт.
функциясы метрика болбойт.
№2- мисал:
функциясын текшеребиз.
d(x, y) ≥0, 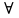 x , y
x , y ; (терс эместик акциомсы)
; (терс эместик акциомсы)
бул акциома аныктамага ылайык аткарылышына шек жок.
d(x, y) = 0, x = y; (теёдештик акциомасы)
бул акциоманы текшерип къръб\з
демек аткарылат.
d(x, y) = d(y, x); (симметриялуулук акциомасы);
жана
жана (1)
(2)
Мындан (1) =(2) барабар экендиги келип чыгат. Демек бул акциома аткарылат.
d(x, z) ≤ d(x, y) + d(y, z) ; (уч бурчтуктун жактарына карата
акциомасы же уч бурчтук барабарсыздыгы) 
Мисалга алсак
болсун


Демек бул акциома аткарылат.
функциясы метрика болот.
№3- мисал:
Берилген къпт\кт\н метрикалык мейкиндик экендигин т\ш\нд\рг\лъ:
 анык сандарынан турган чект\\ къпт\г\,
анык сандарынан турган чект\\ къпт\г\,  жана
жана  аралыктарында
аралыктарында  формуласы менен аныкталса.
формуласы менен аныкталса.
Берилген къпт\к метрикалык мейкиндик болот,нормаланган мейкиндик да боло алат норма тъмънк\ формула менен туюнтулат

Текшерип кърсък. (Н1), (Н2) аксиомаларынын аткарылышына шек жок. Мындан сырткары, (Н3) аксиоманын аткарылышын кърсът\п турат.
№4- мисал:
 сан огундагы баардык интервалдар къпт\г\,
сан огундагы баардык интервалдар къпт\г\,  метрикасы менен биргеликте метрикалык мейкиндик болобу?
метрикасы менен биргеликте метрикалык мейкиндик болобу?
Берилген къпт\к метрикалык мейкиндик болбойт, анткени (М2) аксиомасын канаатандыра албайт. Чндыгында , мисалга алсак  жана
жана 
 бирок
бирок  Бул (М2) аксиомасына карама- каршы келип жатат.
Бул (М2) аксиомасына карама- каршы келип жатат.
№5- мисал:
R анык сандар къпт\г\,
(R, жубтугу метрикалык мейкиндик болушун текшеребиз. Мында (М1), (М2), (М3) аксиомаларынын аткарылышына шек жаратпайт, болгону \ч бурчтуктар барабарсыздыгынын аткарылышын текшеребиз. демек, (М4) аксиомасы да аткарылышы кър\н\п турат.
жубтугу метрикалык мейкиндик болушун текшеребиз. Мында (М1), (М2), (М3) аксиомаларынын аткарылышына шек жаратпайт, болгону \ч бурчтуктар барабарсыздыгынын аткарылышын текшеребиз. демек, (М4) аксиомасы да аткарылышы кър\н\п турат.
№6- мисал:
 баардык къп м\чълър къпт\г\, мында
баардык къп м\чълър къпт\г\, мында  R,
R,  жана
жана  функцияларынын арасындагы аралык тъмънк\ формула менен аныкталса
функцияларынын арасындагы аралык тъмънк\ формула менен аныкталса
 Бул жубтукту метрикалык мейкиндик болушун аныктайбыз.
Бул жубтукту метрикалык мейкиндик болушун аныктайбыз.

 жана
жана  Андан ары
Андан ары  R болсо
R болсо  (Н2) аксиомасы аткарылат .
(Н2) аксиомасы аткарылат .  (Н3) аксиомасы аткарылышы далилденди. Мындан къп м\чън\н нормаланган экендиги аныкталды, андай болсо метрикалык мейкиндик болушу анык .
(Н3) аксиомасы аткарылышы далилденди. Мындан къп м\чън\н нормаланган экендиги аныкталды, андай болсо метрикалык мейкиндик болушу анык .
№7- мисал:
Анык сандар талаасында  евкилиддик мейкиндиги
евкилиддик мейкиндиги 
 метрикасы менен биргеликте нормаланган мейкиндик болушун далилдегиле.
метрикасы менен биргеликте нормаланган мейкиндик болушун далилдегиле.
Далилдъъ:
скалярдык къбъйт\\ аксиомасында  жана
жана  Андан сырткары ,
Андан сырткары , 
 Шварцтын барабарсыздыгынан
Шварцтын барабарсыздыгынан 
алабыз. Мындан \ч бурчтуктар барабарсыздыгынын аткарылышы кър\н\п турат.
№8- мисал:
Эгерде Х къпт\г\ндъ  метрика болсо анда
метрика болсо анда
 функциясы да метрика экендигин далилдегиле.
функциясы да метрика экендигин далилдегиле.
Далилдъъ. 

 жана
жана 
(М4) аксиомасынын аткарылышын текшеребиз





 метрика, анда
метрика, анда  Мындан тъмънк\н\ алабыз башкача айтканда
Мындан тъмънк\н\ алабыз башкача айтканда 
5.Метрикалык мейкиндиктин колдонулушу
№9- мисал:
Берилген мейкиндиктерде тъмънк\ функциянын нормасын эсептегиле 
а)  мейкиндигинде
мейкиндигинде
б)  мейкиндигинде
мейкиндигинде
в)  мейкиндигинде
мейкиндигинде
Чыгаруу
а) 
б)
в)
№10- мисал:
Берилген мейкиндикте тъмънк\ функциялардын аралыктарын эсептегиле  жана
жана 
а)  мейкиндигинде
мейкиндигинде
б)  мейкиндигинде
мейкиндигинде
в)  мейкиндигинде
мейкиндигинде
Чыгаруу.
а)
б)
в)
№11- мисал:
Координаталык тгиздикте  жана
жана чекиттеринин арасындагы аралыкты эсептъъ \ч\н метрикасын колдонуп берилген чекиттердин арасындагы аралыкты тапкыла.
чекиттеринин арасындагы аралыкты эсептъъ \ч\н метрикасын колдонуп берилген чекиттердин арасындагы аралыкты тапкыла.
а)
Жообу: 3
б)
Жообу: 4
№12- мисал:
Координаталык тгиздикте  жана
жана чекиттеринин арасындагы аралыкты эсептъъ \ч\н метрикасын колдонуп борбору координата башталышындагы радиусу 2 болгон айлананын теёдемесин м\нъздъг\лъ.
чекиттеринин арасындагы аралыкты эсептъъ \ч\н метрикасын колдонуп борбору координата башталышындагы радиусу 2 болгон айлананын теёдемесин м\нъздъг\лъ.
Ж ообу:

№13- мисал:
Координаталык тгиздикте  жана
жана чекиттеринин арасындагы аралыкты эсептъъ \ч\н метрикасын колдонуп берилген чекиттердин арасындагы аралыкты тапкыла.
чекиттеринин арасындагы аралыкты эсептъъ \ч\н метрикасын колдонуп берилген чекиттердин арасындагы аралыкты тапкыла.
а )
Жообу: 2
б)
Жообу:5
№14- мисал:
Координаталык тгиздикте  жана
жана чекиттери \ч\н \н метрикасын колдонуп берилген чекиттердин арасындагы аралыкты тапкыла.
чекиттери \ч\н \н метрикасын колдонуп берилген чекиттердин арасындагы аралыкты тапкыла.
а)
Жообу: 2
б)
Жообу: 3
№15- мисал:
К оординаталык тгиздикте  жана
жана чекиттери \ч\н \н метрикасын колдонуп берилген чекиттердин арасындагы аралыкты тапкыла.
чекиттери \ч\н \н метрикасын колдонуп берилген чекиттердин арасындагы аралыкты тапкыла.
а)
Жообу: 4
б)
Жообу: 4
6. Кортунду
Бул иште метрикалык мейкиндик т\ш\н\г\н т\ш\нд\р\\гъ аракет жасалды жана нормаланган мейкиндик да метрикалык мейкиндик болоору т\ш\нд\р\лд\. Булардан сырткары ар кандай метрикалардын далилдъълър\ кърсът\лд\. Метирикалык мейкиндикке карата мисалдар келтирилди. Бул ишти колдонуучу метрикалык мейкиндик т\ш\н\г\н кандай колдоноору тууралуу т\ш\н\к алса болот. Ар бир колдонуучунун позициясында жазууга аракет жасалды. Метрикалык мейкиндик т\ш\н\г\ ътъ кеёири т\ш\н\к, кызыккандар бул ишти улантып изилдесе болот.
7. Колдонуган адабияттар
1. Бичегкуев М.С. Метрические пространства: Теория, задачи, решения. – Москва-Ижевск:НИЦ “Регулярная и хаотическая динамика”, 2005. – 192с
2.
3. А.С. Кутузов МЕТРИЧЕСКИЕ ПРОСТРАНСТВА
Учебное пособие Троицк 2012
4.
5.
Решение задач по функциональному анализу : метод. указания к
практ. занятиям для бакалавров техн. направлений подготовки очной
формы обучения / сост.: Р. В. Ульверт, О. Ю. Балашова ; Сиб. гос.
аэрокосмич. ун-т. – Красноярск, 2015. – 34 с.
© Сибирский
5







 ыргыз республикасы билим бер\\ министирлиги
ыргыз республикасы билим бер\\ министирлиги
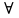 x , y
x , y ; (терс эместик аксиомсы)
; (терс эместик аксиомсы)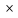

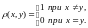 метрикасы менен метрикалык мейкиндик болот жана ал дискреттикит (\зг\лт\кт\\) мейкиндик деп аталат.
метрикасы менен метрикалык мейкиндик болот жана ал дискреттикит (\зг\лт\кт\\) мейкиндик деп аталат.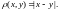 метрикасы менен метрикалык мейкиндик болот.
метрикасы менен метрикалык мейкиндик болот.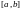 кесиндисинде \зг\лт\кс\з аныкталган
кесиндисинде \зг\лт\кс\з аныкталган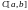 функциялардын къпт\г\
функциялардын къпт\г\  бирдей ченемдеги метрикасы менен метрикалык мейкиндик болот.
бирдей ченемдеги метрикасы менен метрикалык мейкиндик болот. аткарылат.
аткарылат.  аткарылат
аткарылат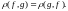 аткарылат
аткарылат
 Анда
Анда  жана
жана 
 Жыйынтыгында баардык х \ч\н тъмънк\н\ алабыз:
Жыйынтыгында баардык х \ч\н тъмънк\н\ алабыз: 
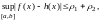 башкача айтканда
башкача айтканда 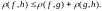
 формуласы менен аныкталган баардык
формуласы менен аныкталган баардык 









