Методическая разработка урока на тему "Решение прикладных задач с помощью определенного интеграла. Вычисление объемов тел."

Волоколамский аграрный техникум «Холмогорка»

Утверждено

на заседании цикловой комиссии

экономических дисциплин

Пр. № ________

от «___» _______________ 200 г.

Председатель ЦК

Акатова Т.Ю. ________________

Рассмотрено

зав. методкабинетом

Пр. № _______

от «_____»_____________ 200 г.

Пантюхова Л.А. ______________

МЕТОДИЧЕСКАЯ РАЗРАБОТКА

комбинированного урока по дисциплине «Математика»

Тема: «Решение прикладных задач с помощью определенного интеграла.

Вычисление объемов тел вращения»

Разработана

преподавателем математики

Кутейниковой Т.А.

Волоколамск

План методической разработки

Стр.

Аннотация ………………………………………………………………………… 3

1. Введение ………………………………………………………………………. 4

1. Основная часть

а) План урока ………………………………………………………….. 5

б) Содержание этапов урока (план - конспект) …………………….. 6

в) Рекомендации по планированию урока …………………………… 11

1. Заключение …………………………………………………………………….. 12

1. Литература ……………………………………………………………………… 13

1. Приложения

а) Приложение 1 ……………………………………………………….. 14

б) Приложение 2 ……………………………………………………… 14

в) Приложение 3 ………………………………………………………. 15

г) Приложение 4 ………………………………………………………. 15

Аннотация

В данной методической разработке приведен один из возможных вариантов планирования занятия по математике, показаны методы активизации мыслительной деятельности студентов и применение различных форм обучения.

Методическая разработка предназначена для преподавателей математики средних специальных заведений. Также может быть интересной и преподавателям других дисциплин.

Введение

Одной из мер повышения качества подготовки специалистов со средним специальным образованием является совершенствование методики преподавания предмета.

Самостоятельная работа студентов является необходимым условием их успешного обучения при изучении любого предмета. Этот вид работы студентов можно применять на любом этапе урока. При этом самостоятельная работа может быть дифференцированной, индивидуальной, выполняться в группе, по вариантам.

В данной методической разработке представлено применение элементов самостоятельной работы на различных этапах урока.

В урок также включены элементы личностно-ориентированного обучения, такие как дифференцированные задания и рефлексия.

Этап	Время	Методы обучения и методические приемы	Средства обучения	Формы
1. Организационный момент:	5 мин.			Фронтально
2. Проверка знаний учащихся: Индивидуальный опрос по карточкам Знание понятий вычисление определенных интегралов составление формул вычисления площади фигуры	20 мин.	репродуктивный репродуктивный частично-поисковый частично-поисковый	Карточки с дифференцированными заданиями Таблица опроса «Ромашка» Таблички Таблички	Самостоятельная Индивидуальная Фронтальная Фронтальная Фронтальная
3. Изложение нового материала: 1) Объемы тел и их свойства Применение метода интегрирования к вычислению объемов тел	15 мин.	обяъснительно-иллюстративный объяснительно-иллюстративный	Сообщение студента Сообщение студента Плакат с изображением фигуры вращения	Самостоятельная Индивидуальная Самостоятельная Индивидуальная
4. Закрепление изученного материала Устная работа: составление формул объема	5 мин.	частично-поисковый	Таблички с изображениями фигур вращения	Фронтальная
2) составление алгоритма решения задач данного типа решение задач с готовым чертежом и со сформулированным словесно условием выполнение заданий по вариантам	10 мин. 15 мин. 15 мин.	частично-поисковый частично-поисковый частично-поисковый	Таблички с алгоритмом Таблички с задачами Карточки с заданиями	Фронтальная Фронтальная Самостоятельная работа
5. Домашнее задание	1 мин.		Запись на доске	Фронтально
6. Рефлексия	4 мин.	Опрос	Контрольный лист	Фронтально
Итого: 1 ч. 30 мин.

ПЛАН УРОКА ПО ТЕМЕ

«Решение прикладных задач с помощью определенного интеграла. Вычисление объемов тел вращения»

План - конспект

План занятия № 50. Дата Группа

По дисциплине Математика

Тема Решение прикладных задач с помощью определенного интеграла. Вычисление объемов тел.

Цели

Методическая: показать применение элементов самостоятельной работы студентов на различных этапах урока.

Образовательная: формировать знания о применении интегралов как методе решения задач, о методе вычисление объема тел

Воспитывать аккуратность при оформлении задач

Развивать алгоритмическое мышление

Тип урока. Урок комбинированный

Методы: репродуктивный, частично – поисковый.

Формы: фронтальная работа, индивидуальная

Оборудование. Таблица неопределенных интегралов, плакат с рисунком тела вращения, таблички с интегралами, таблички для опроса (в виде ромашки), таблички с изображением геометрических фигур, сообщения студентов, контрольные листы.

Время проведения: 90 минут.

Место проведения: кабинет математики (№ 316).

Ход урока.

Организационный момент. 1) отсутствующие; 2) дежурные; 3) ознакомить с правилами работы на уроке и заполнения контрольных листов.

Проверка знаний учащихся – 1) опрос по индивидуальным карточкам заданий (дифференцированным) на вычисление площади криволинейной трапеции (4 учащихся); 2) опрос по карточкам (задачи) у доски (2 учащихся); 3) фронтальный опрос (знание понятий - ромашка) и по табличкам интегралов (правильный ответ – 1 балл, учет с помощью счетных палочек). Подведение итогов как подготовились к уроку, завершение этапа подготовки к занятию – заполнение контрольного листа. Сообщение темы урока, постановка цели, задачи

Сегодня мы познакомимся с применением определенного интеграла для вычисления объемов тел вращения и будем учиться решать такие задачи.

Изложение нового материала, применяемая методика – сообщения учащихся (2):

1. Объемы тел и их свойства. (Сообщение 1)

2. Применение метода интегрирования к вычислению объемов тел. Записать формулы. (Сообщение 2)

Закрепление изученного материала, применяемая методика

1. Устная работа с табличками: выразить объем тела через определенный интеграл (5 табличек с изображенными фигурами) – правильный ответ – 1 балл.

1. Составить алгоритм решения задач данного типа:

Найти ООФ

Построить графики функций на отрезке

Определить фигуру вращения

Найти пределы интегрирования x=a, x=b Из графика функции или Определить отрезок у=f(x), решив систему уравнений y=g(x);

Записать формулу объема

Вычислить объем

1. Фронтально (решение 3-х задач):

две задачи с готовым чертежом:

Найдите объем фигуры, полученной вращением криволинейной трапеции, ограниченной данными линиями, 1) вокруг оси абсцисс (Ох, у=0) (96/5)и 2) вокруг оси ординат (Оу, х=0) (128/7)

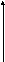
у=х^1/3

у

2

1

У=0

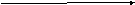
0

8

х

1

третья словесно сформулированная задача:

Найдите объем фигуры, полученной вращением криволинейной трапеции, ограниченной данными линиями у=3х, у=0 и х=2 вокруг оси абсцисс. (24)

1. Самостоятельное выполнение заданий (решение трех задач по нарастающей сложности по вариантам в виде соревнования) – на каком варианте больше добравшихся до 1-го места на пьедестале. Работа ограничена по времени. Решение проверяют сами по окончании времени по представленным образцам, и выставляют себе оценки.

Вариант 1

1) Найдите объем фигуры, полученной вращением криволинейной трапеции, ограниченной данными линиями у =0,5х, х=2 и х=1, у=0 вокруг оси абсцисс.(7/12)

2) Найдите объем фигуры, полученной вращением криволинейной трапеции, ограниченной данными линиями вокруг оси абсцисс

У=0

х

0

1

4

Вариант 2

1) Найдите объем фигуры, полученной вращением криволинейной трапеции, ограниченной данными линиями у =х, х=1 и х=3, у=0 вокруг оси абсцисс. (26/3)

2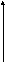) Найдите объем фигуры, полученной вращением криволинейной трапеции, ограниченной данными линиями вокруг оси абсцисс

у

У=4-х

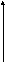
у

х

У=1+х

0

1

2

У=0

Итог урока

Как можно найти объем тела, полученного вращением криволинейной трапеции вокруг оси Ох (Оу)?

Задание для самостоятельной работы во внеурочное время – учить материалы конспекта,

П. 47(Яковлев).

П. 8.3.2, 8.3.3 (Пехлецкий И.Д.)

№ 8.75 – Найти объем тела, образованного вращением фигуры, ограниченной указанными линиями х=у²; х=1; у=0 (вокруг осей Ох и Оу).

Рефлексия Понравился ли вам урок? Что сложного было сегодня на уроке?

Что вам понравилось больше всего?

Оцените свою работу на уроке:

если

• вы работали активно, все поняли – « 5 баллов»

• вы работали недостаточно активно, могу лучше – «4 балла»

• скучали, но включались в работу - «3 балла»

• витали в облаках, но с доски и под диктовку что-то писали – «2 балла»

• не работали сами и мешали работать другим – « -2 балла»

Подведение итогов урока Подсчитать число баллов по контрольному листу и поставить себе оценку.

Сдать тетради для проверки.

Рекомендации по планированию урока

В связи с тем, что изучается большой объем материала, а время изучения ограничено небольшим количеством часов, необходимо на каждом занятии выбирать приоритетное направление деятельности студентов.

На данном уроке основным видом деятельности служит формирование умения составлять формулы для вычисления площадей фигур и вычисления объемов тел вращения, а также умения составлять алгоритмы решения задач. Исходя из этих соображений, и были подобраны упражнения и задачи к уроку.

Заключение

Абстрактный характер математики не является признаком ее оторванности от действительного мира, поскольку любое познание связано с абстрагированием, моделированием реальных процессов. Поэтому огромное значение имеет показ математических приложений для естествознания, техники, экономики, для создания новых подходов к решению реальных проблем и вытекающих из них задач.

В этом смысле приложения определенного интеграла являются хорошей иллюстрацией. Но также представляется возможным и формирование представления об интегрально-дифференциальном исчислении как методе, применимом к решению задач из разных областей знаний.

Эти подходы я и попыталась реализовать в данной методической разработке.

Литература

1. И.Д. Пехлецкий. Среднее профессиональное образование. Математика. 2-е издание, М.: Издательский центр «Академия», 2003. – 304 с.

2. А.А. Дадаян. Математика. Профессиональное образование. М.: ФОРУМ: ИНФРА-М, 2005. – 552 с.

3. Л.Ю. Сергиенко, П.И. Самойленко. Планирование учебного процесса по математике. М.: «Высшая школа», 1987. – 424 с.

4. Г.Д. Глейзер, С.М. Саакян, И.Г. Вяльцева, А.С. Алексеев. Алгебра и начала анализа. Учебное пособие для старших классов общеобразовательных и среднеспециальных учебных заведений. Под ред. Г.Д. Глейзера. 6-е издание. М.: «Просвещение», «Владос», 1995. – 432 с.

5. Тесты. Математика. 5 – 11 классы. М., «Олимп», «Издательство АСТ», 2000. - 432с. Составители: Максимовская М.А., Пчелинцев Ф.А., Уединов А.Б., Чулков П.В.

6. П.И. Алтынов. Тесты. Алгебра и начала анализа. 10 – 11 классы. Учебно-методическое пособие. 4 - е издание. М.. «Дрофа», 2000.

7. Р.Д. Лукин, Т. К. Лукина, М.С. Якунина. Устные упражнения по алгебре и началам анализа. Книга для учителя. М., «Просвещение», 1989. – 96 с.

Приложение 1

3) Найдите объем фигуры, полученной вращением криволинейной трапеции,

ограниченной данными линиями у =х³, х=0 и х=1, у=0 вокруг оси абсцисс.(/7)

3) Найдите объем фигуры, полученной вращением криволинейной трапеции,

ограниченной данными линиями у =х², х=0 и х=1, у=0 вокруг оси абсцисс.(/5)

На «3»

Найдите площадь фигуры, ограниченной линиями у=2х, у=0, х=1 и х=3.

Найдите площадь фигуры, ограниченной линиями у= - 4х, у=0, х= - 1 и х=0.

Найдите площадь фигуры, ограниченной линиями у=6х, у=0, х=1 и х=2.

Найдите площадь фигуры, ограниченной линиями у= - 4х, у=0, х= -2 и х= -1

На «4»

Найдите площадь фигуры, ограниченной линией у=х² - х и осью абсцисс.

Найдите площадь фигуры, ограниченной линией у= 4х² - 1 и осью абсцисс.

Найдите площадь фигуры, ограниченной линией у=3х² - 6х и осью абсцисс.

Найдите площадь фигуры, ограниченной линией у=2х - х² и осью абсцисс.

На «5»

Найдите площадь фигуры, ограниченной линиями у=2х – х² и у=х.

Найдите площадь фигуры, ограниченной линиями у=х² и х=у².

Найдите площадь фигуры, ограниченной линиями у=х³/4 и у=(2х).

Найдите площадь фигуры, ограниченной линиями у=х, у=6 – х и у=0.

Задача №1

Найдите площадь фигуры, ограниченной линиями у= sin x и у= cos x, х= /4 и х= .

Задача №2

Материальная точка движется прямолинейно со скоростью v(t)= 8t – 4 (м/с). Какое расстояние пройдет материальная точка за первые 3 секунды своего движения?

(Материальная точка движется прямолинейно со скоростью v(t)= 3t – 2 (м/с). Какое расстояние пройдет материальная точка за первые 2 секунды своего движения?)

(Материальная точка движется прямолинейно со скоростью v(t)= 6t² – 4t (м/с). Какое расстояние пройдет материальная точка за первые 3 секунды своего движения?)

(Материальная точка движется прямолинейно со скоростью v(t)= 12t + 4 (м/с). Какое расстояние пройдет материальная точка за первые 3 секунды своего движения?)

Определение первообразной.

Как проверить правильно ли найдена первообразная данной функции?

14