Государственное бюджетное профессиональное образовательное
учреждение
«Волгоградский техникум водного транспорта имени адмирала флота
Н. Д. Сергеева»
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ
ВЫПОЛНЕНИЯ ПРАКТИЧЕСКИХ РАБОТ
ПО УЧЕБНОЙ ДИСЦИПЛИНЕ
ОУД.03 «МАТЕМАТИКА:
АЛГЕБРА И НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА; ГЕОМЕТРИЯ»
для студентов 1 курса
очной формы обучения
(1 семестр)
2015
| Рассмотрена на заседании Цикловой комиссии преподавателей ООД Председатель МЦ ______________ ФИО
Протокол от « » 2015 г № ___ | УТВЕРЖДАЮ Директор ГБПОУ «Волгоградский техникум водного транспорта им. адмирала флота Н.Д. Сергеева» _____________ А.Ф. Кравченко
«____» _____________ 2015 г.
|
Методические указания для выполнения практических работ являются частью основной профессиональной образовательной программы ГБПОУ «Волгоградский техникум водного транспорта им. адмирала флота Н.Д. Сергеева» для профессий 2 6.01.07 МАТРОС, 26.01.09 МОТОРИСТ СУДОВОЙ учебной дисциплины «Математика: Алгебра и начала математического анализа; геометрия».
Методические указания для выполнения практических работ адресованы студентам очной формы обучения.
Методические указания включают в себя учебную цель, краткие теоретические и учебно-методические материалы по темам 1-го семестра, вопросы для закрепления теоретического материала, задания для практической работы студентов, порядок и требования к оформлению отчета о проделанной работе.
Организация-разработчик: ГБПОУ «Волгоградский техникум водного транспорта
им. адмирала флота Н.Д. Сергеева»
Разработчик:
Чайка Наталья Георгиевна, преподаватель высшей квалификационной категории ГБПОУ «Волгоградский техникум водного транспорта им. адмирала флота Н.Д. Сергеева»
СОДЕРЖАНИЕ
1. Пояснительная записка…………………………………………………..4
2. Перечень наименований практических работ …………………………5
3. Методические указания к выполнению практических работ…………………………………………………………………… 6-31
4. Перечень литературы и средств обучения ……………………………32
5. Контроль и оценка результатов освоения дисциплины……………...32
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Краткая характеристика методического пособия, цели и задачи. Место практических работ в курсе дисциплины.
В данном пособии представлены методические указания к выполнению практических работ по дисциплине «Математика: алгебра и начала математического анализа; геометрия», которые направлены на обобщение, систематизацию, закрепление полученных теоретических знаний по конкретным темам дисциплины.
Методические указания составлены в соответствии с Приказом Министерства образования и науки от 17.05.2012 г,№413 «Об утверждении федерального образовательного стандарта среднего (полного) общего образования» и способствуют организации самостоятельной работы студентов как на занятиях с преподавателем, так и для самостоятельного образования.
Методические указания содержат необходимый теоретический минимум, включающий определения, теоремы и формулы, затем даются примеры и задания, полностью охватывающие данные темы и сопровождаются подробными решениями. Затем предлагаются самостоятельные задания, которые выполняются по аналогии и контрольные вопросы для проверки знаний по теме.
Учебная дисциплина «Математика: алгебра и начала математического анализа; геометрия» изучается как профильный учебный предмет при освоении профессии 26.01.07 Матрос, 26.01.09 Моторист судовой в объеме 428 часов (обязательная аудиторная учебная нагрузка -285 часов из них 100 часов –теоретическое обучение,152 часа - лабораторные и практические занятия,30-контрольняе работы и 143 часа-внеаудиторная самостоятельная работа обучающегося)
Содержание рабочей программы учебной дисциплины, согласовано с требованиями федерального государственного стандарта среднего (полного) общего образования профильного уровня.
Выполнение практических работ поможет студентам освоить учебную дисциплину и подготовиться к сдаче экзамена.
Организация и порядок проведения практических работ.
Практические работы проводятся после изучения теоретического материала в учебном кабинете математики. Обучающие должны иметь методические рекомендации по выполнению практических работ, конспекты лекций, измерительные и чертежные инструменты, средство для вычислений.
Техника безопасности при выполнении практических работ.
При работе в учебном кабинете запрещается:
находиться в учебном кабинете в отсутствии преподавателя;
вставать со своего места и ходить по кабинету без разрешения преподавателя;
размещать на рабочем месте посторонние предметы.
Обучающий обязан:
спокойно, не торопясь, не задевая столы входить в кабинет и занимать отведенное ему место;
во время перемены покинуть кабинет;
работать на закрепленном за ним месте;
приступать к работе по указанию преподавателя;
по окончанию работы сдавать выданные материалы преподавателю;
привести свое рабочее место в порядок.
2. Перечень наименований практических работ
| Темы практических занятий | страницы |
| Практическое занятие № 1. «Действия с приближенными величинами Оценка погрешностей приближений». | 6 |
| Практическое занятие № 2. «Действия над степенями с рациональным и действительным показателем». | 7 |
| Практическое занятие № 3. «Показательные уравнения, и методы их решений» | 10 |
| Практическое занятие № 4. «Преобразование логарифмических выражений». | 13 |
| Практическое занятие № 5. «Логарифмические уравнения, и методы их решения». | 15 |
5.МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ ПРАКТИЧЕСКИХ РАБОТ
ПРАКТИЧЕСКОЙ РАБОТЫ № 1
Учебная дисциплина: «МАТЕМАТИКА:
АЛГЕБРА И НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА; ГЕОМЕТРИЯ»
№1.1Тема: «Действия с приближенными величинами. Оценка погрешностей».
Цель занятия: Обобщить и систематизировать умения выполнять расчеты с приближенными величинами и оценивать погрешности.
Оборудование: методическое указание к выполнению практической работы, лекции, учебная литература, тетрадь для оформления практических работ.
Норма времени: 90 мин.
Теоретические сведения
При всех технических расчетах имеют дело с величинами, полученными в результате тех или иных измерений или наблюдений. Так как любые измерения не могут дать точного значения измеряемых величин, то при расчетах пользуются приближенными значениями этих величин, имеющими большую или меньшую степень точности.
Определение: Абсолютной погрешностью приближенного значения называется модуль разности точного и приближенного значений.
Определение: Относительной погрешностью приближенного значения называется отношение абсолютной погрешности к модулю приближенного значения.
Примеры и последовательность выполнения заданий
Действия с приближенными величинами
Пример: Пусть а=5,0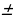 0,1 , в=3,4
0,1 , в=3,4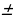 0,2 . Вычислить а+в, а-в, ав, а/в. Оценить относительные погрешности результатов для ав и а/в.
0,2 . Вычислить а+в, а-в, ав, а/в. Оценить относительные погрешности результатов для ав и а/в.
Решение. Здесь х=5,0 , у=3,4 , Δax= Δa=0,1 , Δby= Δb=0,2. Тогда Δa+b= Δa-b= Δa+ Δb =0,1+0,2=0,3 ,откуда а+в=8,4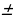 0,3 и а-в=1,6
0,3 и а-в=1,6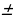 0,3.
0,3.
Найдем относительные погрешности:
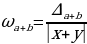 =
= 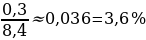
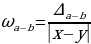 =
=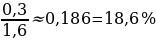
Δab=уΔa+хΔb=3,4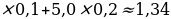
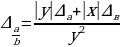 =
=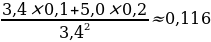
Следовательно, ав=17,0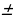 1,34 , а/в=1,47
1,34 , а/в=1,47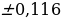 .
.
Оценим относительные погрешности полученных результатов для ав и а/в :
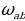 =
=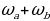 =
=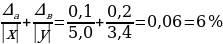
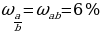
Выполнить следующие задания.
1 вариант
Задание 1. Найдите относительную погрешность и выразите ее в процентах. В приближенном значении x определите верные и сомнительные цифры:
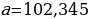 ,
, 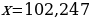
Задание 2.
Пусть а=7,0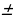 0,2 , в=5,4
0,2 , в=5,4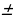 0,3 . Вычислить а+в, а-в, ав, а/в.
0,3 . Вычислить а+в, а-в, ав, а/в.
Оценить относительные погрешности результатов для ав и а/в.
2 вариант
Задание 1. Найдите относительную погрешность и выразите ее в процентах. В приближенном значении x определите верные и сомнительные цифры:
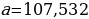 ,
, 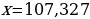
Задание 2.
Пусть а=9,0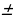 0,3 , в=6,4
0,3 , в=6,4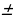 0,2. Вычислить а+в, а-в, ав, а/в.
0,2. Вычислить а+в, а-в, ав, а/в.
Оценить относительные погрешности результатов для ав и а/в.
Порядок выполнения работы
При выполнении практической работы надо придерживаться следующих правил:
1.Практическую работу следует выполнять в тетради, синей или черной шариковой ручкой, оставляя поля.
2.На обложке тетради должны быть ясно написаны название дисциплины, фамилия, инициалы студента, номер группы.
3. В заголовке работы должны быть указаны номер практической работы, тема практической работы, номер варианта.
4.Перед решением каждого задания надо выписать полное условие.
5.Решение заданий следует излагать подробно и аккуратно, объясняя и мотивируя все действия решения.
6. После получения проверенной работы, студент должен исправить все отмеченные ошибки.
Пояснение и рекомендации к выполнению работы.
Содержание отчета:
1. Наименование работы, номер работы, вариант.
2. Цель работы.
3. Оборудование, используемое для выполнения практической работы.
4. По необходимости краткая теория.
5. Номер задания и его условие.
6. Последовательность выполнения работы, необходимые решения.
7.Ответы на контрольные вопросы.
8. Выводы о проделанной работе.
9.Используемая литература: перечень справочной литературы, таблиц
Контрольные вопросы.
Абсолютная погрешность: определение, формула абсолютной погрешности.
Относительная погрешность: определение, формула относительной погрешности.
3.Действия с приближенными величинами. Оценка погрешностей приближений
Рекомендуемая литература
Башмаков, М.И. Алгебра и начала анализа 10 кл. Базовый уровень : учебник для общеобразоват. учреждений - М.: Дрофа, 2014.-288 с.
Башмаков М.И. Математика: учебник для учреждений нач. и сред. проф. образования. – М.: Издательский центр «Академия», 2012.-256 с.
Башмаков М.И. Алгебра и начала анализа 11 кл. Базовый уровень: учебник для общеобразоват .учреждений- М: Издательский центр «Академия»», 2010.-288с.
Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В. Математика: алгебра и начала математического анализа, геометрия 10 класс, учеб. для общеобразоват. организаций: базовый и углубл. уровни -М.: Просвещение,2014.-431с
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ
ПРАКТИЧЕСКОЙ РАБОТЫ № 2
Учебная дисциплина: «МАТЕМАТИКА:
АЛГЕБРА И НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА; ГЕОМЕТРИЯ»
№ 2.1-2.2 Тема: «Действия над степенями с рациональным и действительным показателем».
Цель занятия: Обобщить и систематизировать знания по теме «Свойства корней и степеней»; закрепить умения использовать полученные знания для преобразования алгебраических выражений.
Оборудование: методическое указание к выполнению практической работы, лекции, учебная литература, тетрадь для оформления практических работ.
Норма времени: 180 мин.
Теоретические сведения
Степенью называется выражение вида: 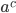 , где:
, где:
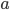 — основание степени;
— основание степени;
 — показатель степени.
— показатель степени.
Степень с натуральным показателем {1, 2, 3,...}
Определим понятие степени, показатель которой — натуральное число (т.е. целое и положительное).
По определению: 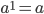 .
.
Возвести число в квадрат — значит умножить его само на себя: 
Возвести число в куб — значит умножить его само на себя три раза: 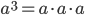 .
.
Возвести число в натуральную степень 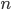 — значит умножить число само на себя
— значит умножить число само на себя 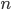 раз:
раз:
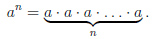
Степень с целым показателем {0, ±1, ±2,...}
Если показателем степени является целое положительное число:
 , n 0
, n 0
Возведение в нулевую степень:
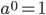 , a ≠ 0
, a ≠ 0
Если показателем степени является целое отрицательное число:
 , a ≠ 0
, a ≠ 0
Прим: выражение 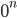 не определено, в случае n ≤ 0. Если n 0, то
не определено, в случае n ≤ 0. Если n 0, то 
Пример 1.
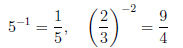
Степень с рациональным показателем
Если:
a 0;
n — натуральное число;
m — целое число;
Тогда:
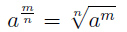
Пример 2.
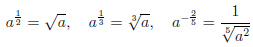
Свойства степеней
| Произведение степеней | 
|
| Деление степеней | 
|
| Возведение степени в степень | 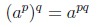
|
Арифметический квадратный корень  — это неотрицательное число, квадрат которого равен
— это неотрицательное число, квадрат которого равен 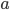 , a ≥ 0. При a — выражение
, a ≥ 0. При a — выражение  не определено, т.к. нет такого действительного числа, квадрат которого равен отрицательному числу
не определено, т.к. нет такого действительного числа, квадрат которого равен отрицательному числу 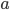 .
.
Корень из квадрата
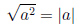
Например,  . А решения уравнения
. А решения уравнения  соответственно
соответственно 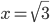 и
и 
Кубический корень
Кубический корень из числа 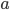 — это число, куб которого равен
— это число, куб которого равен 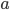 . Кубический корень определен для всех
. Кубический корень определен для всех 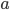 . Его можно извлечь из любого числа:
. Его можно извлечь из любого числа: 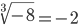 .
.
Корень n-ой степени
Корень 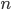 -й степени из числа
-й степени из числа 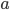 — это число,
— это число, 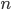 -я степень которого равна
-я степень которого равна 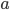 .
.
Если 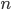 — чётно.
— чётно.
Тогда, если a корень n-ой степени из a не определен.
Или если a ≥ 0, то неотрицательный корень уравнения 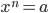 называется арифметическим корнемn-ой степени из a и обозначается
называется арифметическим корнемn-ой степени из a и обозначается 
Если 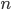 — нечётно.
— нечётно.
Пример3.
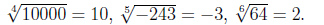
Примеры и последовательность выполнения заданий
Пример 1. Вычислить
а) 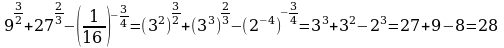
б) 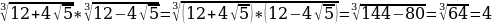
в)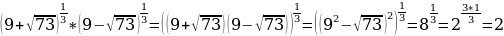
г) 
д) 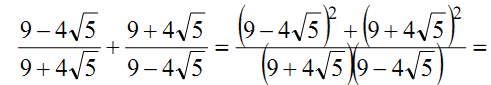

Пример 2. Упростить выражение и найти его значение
а) 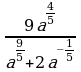 при а = 5
при а = 5
Решение

б) 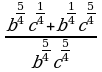 при b=2, c=5
при b=2, c=5
Решение

Пример 3. Избавиться от иррациональности в знаменателе
а) 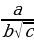 Решение
Решение 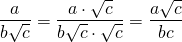
б)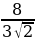 Решение
Решение 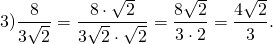
в)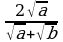 Решение
Решение 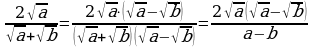 .
.
г) 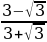 Решение:
Решение: 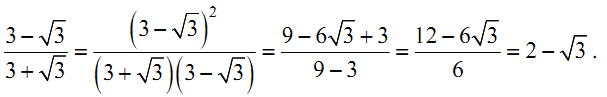
д) 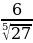 Решение:
Решение: 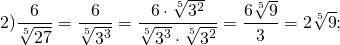
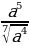 Решение :
Решение : 
Выполните следующие задания
1 вариант
Задание 1. Вычислить
а) 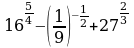 .
.
б) 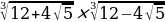 ;
;
в) 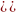 ;
;
г) 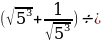 ) ;
) ;
д) 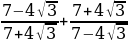 .
.
Задание 2. Упростить выражение и найти его значение
а) 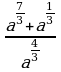 при а = 2
при а = 2
б) 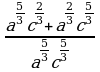 при а=7, с=3
при а=7, с=3
Задание 3. Избавиться от иррациональности в знаменателе
а) 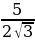 ; б)
; б) 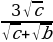 ; в)
; в) 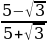 ;
;
г) 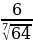 д)
д) 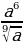
2 вариант
Задание 1. Вычислить
а) 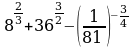 .
.
б) 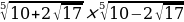 ;
;
в)  ;
;
г) 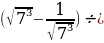 ) ;
) ;
д) 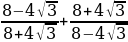 .
.
Задание 2. Упростить выражение и найти его значение
а) 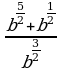 при b=3
при b=3
б) 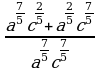 при а=9, с=2
при а=9, с=2
Задание 3. Избавиться от иррациональности в знаменателе
а) 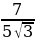 ; б)
; б) 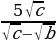 ; в)
; в) 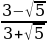 ;
;
г) 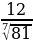 д)
д) 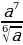
Порядок выполнения работы
При выполнении практической работы надо придерживаться следующих правил:
1.Практическую работу следует выполнять в тетради, синей или черной шариковой ручкой, оставляя поля.
2.На обложке тетради должны быть ясно написаны название дисциплины, фамилия, инициалы студента, номер группы.
3. В заголовке работы должны быть указаны номер практической работы, тема практической работы, номер варианта.
4.Перед решением каждого задания надо выписать полное условие.
5.Решение заданий следует излагать подробно и аккуратно, объясняя и мотивируя все действия решения.
6. После получения проверенной работы, студент должен исправить все отмеченные ошибки.
Пояснение и рекомендации к выполнению работы.
Содержание отчета:
1. Наименование работы, номер работы, вариант.
2. Цель работы.
3. Оборудование, используемое для выполнения практической работы.
4. По необходимости краткая теория.
5. Номер задания и его условие.
6. Последовательность выполнения работы, необходимые решения.
7.Ответы на контрольные вопросы.
8. Выводы о проделанной работе.
9.Используемая литература: перечень справочной литературы, таблиц
Контрольные вопросы.
Корень натуральной степени из числа. Определение.
Свойства корня натуральной степени из числа.
Степень с рациональным показателем. Определение.
Свойства степени с рациональным показателем.
Понятие степени с действительным показателем.
Свойства степени с действительным показателем.
Избавление от иррациональности в знаменателе.
Рекомендуемая литература
Башмаков, М.И. Алгебра и начала анализа 10 кл. Базовый уровень : учебник для общеобразоват. учреждений - М.: Дрофа, 2014.-288 с.
Башмаков М.И. Математика: учебник для учреждений нач. и сред. проф. образования. – М.: Издательский центр «Академия», 2012.-256 с.
Башмаков М.И. Алгебра и начала анализа 11 кл. Базовый уровень: учебник для общеобразоват .учреждений- М: Издательский центр «Академия»», 2010.-288с.
Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В. Математика: алгебра и начала математического анализа, геометрия 10 класс, учеб. для общеобразоват. организаций: базовый и углубл. уровни -М.: Просвещение,2014.-431с
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ
ПРАКТИЧЕСКОЙ РАБОТЫ № 3
Учебная дисциплина: «МАТЕМАТИКА:
АЛГЕБРА И НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА; ГЕОМЕТРИЯ»
№ 2.2 Тема: «Показательные уравнения, и методы их решений».
Цель занятия: Обобщить и систематизировать знания методов решения показательных уравнений; закрепить умения использовать полученные знания при решении показательных уравнений разными методами.
Оборудование: методическое указание к выполнению практической работы, лекции, учебная литература, тетрадь для оформления практических работ.
Норма времени: 180 мин.
Теоретические сведения
Показательными называются уравнения, в которых неизвестная переменная находится только в показателях каких-либо степеней.
Для решения показательных уравнений требуется знать и уметь использовать следующую несложную теорему:
Теорема 1. Показательное уравнение af(x) = ag(x) (где a 0, a ≠ 1) равносильно уравнению f(x) = g(x).
Примеры и последовательность выполнения заданий
Методы решения показательных уравнений
1. Простейшие показательные уравнения
Примеры.
Пример 1. Решите уравнение: 34x-5 = 3x+4 .
Решение.
34x-5 = 3x+4
4x -5 = x+4
3x=9
x = 3 .
Ответ:3
2. Методы преобразования показательных уравнений к простейшим.
A. Метод уравнивания оснований.
Примеры.
Пример 1. Решите уравнение: 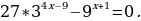
Решение.
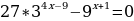
3334x-9- (32)x+1 = 0
33+ (4x-9)- 32(x+1) = 0
34x-6-32x+2 = 0
34x-6 = 32x+2
4x-6=2x+2
2x = 8
x=4. Ответ: 4.
Пример 2. Решите уравнение: 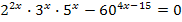 .
.
Решение.
(22)x 3x
3x 5x - 604x-15 =0
5x - 604x-15 =0
(22)x 3x
3x 5x = 604x-15
5x = 604x-15
4x 3x
3x  5x = 604x-15
5x = 604x-15
(4 3
3 5)х= 604x-15
5)х= 604x-15
60x=604x-15
x=4x-15
3x=15
x=5. Ответ: 5.
В. Уравнения, решаемые разложением на множители.
Примеры.
Пример 1. Решите уравнение: x 2x = 2
2x = 2 2x + 8x-16.
2x + 8x-16.
Решение.
x 2x = 2
2x = 2 2x + 8x-16
2x + 8x-16
x 2x - 2
2x - 2 2x = 8
2x = 8 (x-2)
(x-2)
2x  (x-2) - 8
(x-2) - 8 (х-2)
(х-2)
(x-2) ( 2x - 8) = 0
( 2x - 8) = 0 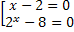
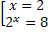
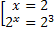
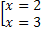 .
.
Ответ: 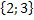
Пример 2 . Решите уравнение: 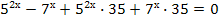
Решение.
52x - 7x - 52x 35 +7x
35 +7x  35= 0
35= 0
(52x - 7x)- (52x 35 +7x
35 +7x  35)= 0
35)= 0
(52х-7х)-35(52х-7х)=0
(52х-7х) 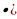 1-35)=0
1-35)=0
(52х-7х)  (-34)=0 , т.к -34
(-34)=0 , т.к -34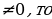
(52х-7х)=0
(52)х=7х
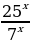 =1
=1
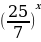 =1
=1
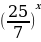 =
=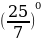 x=0 Ответ: 0.
x=0 Ответ: 0.
С. Уравнения, которые с помощью подстановки 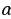 f(x) = t, t0 преобразуются к квадратным уравнениям (или к уравнениям более высоких степеней).
f(x) = t, t0 преобразуются к квадратным уравнениям (или к уравнениям более высоких степеней).
Пусть 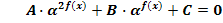 , где А, В, С - некоторые числа. Сделаем замену:
, где А, В, С - некоторые числа. Сделаем замену: 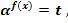
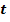 0, тогда A
0, тогда A t2 + B
t2 + B t + C = 0
t + C = 0
Решаем полученное уравнение, находим значения t, учитываем условие t 0 , возвращаемся к простейшему показательному уравнению 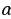 f(x) = t, решаем его и записываем ответ.
f(x) = t, решаем его и записываем ответ.
Примеры.
Пример 1 . Решите уравнение: 22+x - 22-x = 15.
Решение.
22+x - 22-x =1 5
222x - 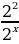 = 15
= 15
4 (2x)2 - 4 = 15 2x
2x
Делаем замену t = 2x, t 0. Получаем уравнение 4t2 - 4 = 15t 4t2 - 15t - 4=0
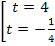 , t =
, t = 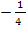 не удовлетворяет условию t 0.
не удовлетворяет условию t 0.
Вернемся к переменной х:
2х = 4
2x = 22
x=2. Ответ: 2
Выполните следующие задания
1 вариант 2 вариант
Решите уравнения:
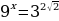
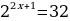
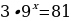
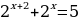
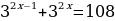
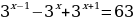
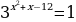
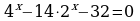
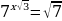
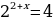
2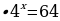
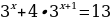
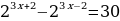
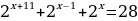
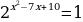
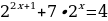
Порядок выполнения работы
При выполнении практической работы надо придерживаться следующих правил:
1.Практическую работу следует выполнять в тетради, синей или черной шариковой ручкой, оставляя поля.
2.На обложке тетради должны быть ясно написаны название дисциплины, фамилия, инициалы студента, номер группы.
3. В заголовке работы должны быть указаны номер практической работы, тема практической работы, номер варианта.
4.Перед решением каждого задания надо выписать полное условие.
5.Решение заданий следует излагать подробно и аккуратно, объясняя и мотивируя все действия решения.
6. После получения проверенной работы, студент должен исправить все отмеченные ошибки.
Пояснение и рекомендации к выполнению работы.
Содержание отчета:
1. Наименование работы, номер работы, вариант.
2. Цель работы.
3. Оборудование, используемое для выполнения практической работы.
4. По необходимости краткая теория.
5. Номер задания и его условие.
6. Последовательность выполнения работы, необходимые решения.
7.Ответы на контрольные вопросы.
8. Выводы о проделанной работе.
9.Используемая литература: перечень справочной литературы, таблиц
Контрольные вопросы.
Какие уравнения называются показательными.
Основные свойства степени с рациональным показателем.
Основные свойства степени с действительным показателем.
Рекомендуемая литература
Башмаков, М.И. Алгебра и начала анализа 10 кл. Базовый уровень : учебник для общеобразоват. учреждений - М.: Дрофа, 2014.-288 с.
Башмаков М.И. Математика: учебник для учреждений нач. и сред. проф. образования. – М.: Издательский центр «Академия», 2012.-256 с.
Башмаков М.И. Алгебра и начала анализа 11 кл. Базовый уровень: учебник для общеобразоват .учреждений- М: Издательский центр «Академия»», 2010.-288с.
Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В. Математика: алгебра и начала математического анализа, геометрия 10 класс, учеб. для общеобразоват. организаций: базовый и углубл. уровни -М.: Просвещение,2014.-431с
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ
ПРАКТИЧЕСКОЙ РАБОТЫ № 4
Учебная дисциплина: «МАТЕМАТИКА:
АЛГЕБРА И НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА; ГЕОМЕТРИЯ»
№ 2.3 Тема: «Преобразования логарифмических выражений. Решение упражнений».
Цель занятия: Обеспечить закрепление понятия логарифм числа; формирование практических навыков преобразования логарифмических выражений на основе изученного теоретического материала (определения и свойств логарифмов).
Оборудование: методическое указание к выполнению практической работы, лекции, учебная литература, тетрадь для оформления практических работ.
Норма времени: 225 мин.
Теоретические сведения
Логарифмом числа b (b 0) По основанию а (a 0, a≠ 1) называют показатель степени, в которую нужно возвести число a, чтобы получить число b: 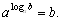
Формулу называют Основным логарифмическим тождеством.
Логарифм числа b по основанию 10 называется Десятичным логарифмом обозначается 
Логарифм по основанию e (e = 2,71828…) называется Натуральным логарифмом и обозначается 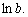
Свойства логарифмов
Пусть 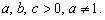 Тогда:
Тогда:
1) 
2) 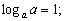
3) 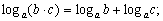
4) 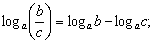
5) 
6) 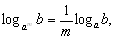
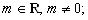
7) 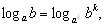
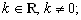
8) 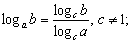
9) 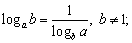
10) 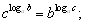
11) 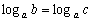 Тогда и только тогда, когда
Тогда и только тогда, когда 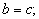
12) 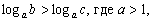 тогда и только тогда, когда
тогда и только тогда, когда 
13)  тогда и только тогда, когда
тогда и только тогда, когда 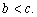
Обобщенные свойства логарифмов
Пусть  и
и 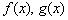 – выражения с переменной. Тогда:
– выражения с переменной. Тогда:
3*) 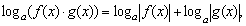 где
где 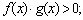
4*) 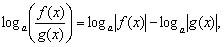 где
где 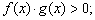
5*) 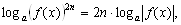 где
где 
6*) 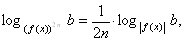 где
где 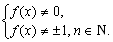
З а м е ч а н и е 1. Следует различать произведение логарифмов 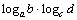 и повторный логарифм
и повторный логарифм 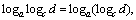
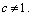
З а м е ч а н и е 2. Степень логарифма может быть записана двумя способами:
 или
или 
Логарифмированием называется операция нахождения логарифма числа или выражения.
Потенцированием называют действие, обратное логарифмированию, т. е. потенцирование – это операция нахождения числа (выражения) по его логарифму. При выполнении этих операций пользуются свойствами логарифмов.
Примеры и последовательность выполнения заданий.
Пример 1. Вычислить. 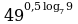
Решение. 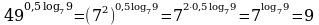
Пример 2. Вычислить.
а) 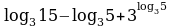
Решение. 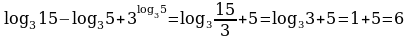
б) 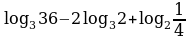
Решение. 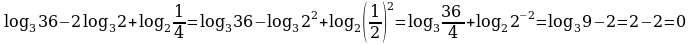 Пример 3. Упростить выражение.
Пример 3. Упростить выражение. 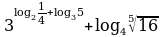
Решение. 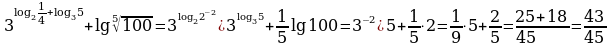
Пример 4. Вычислить. 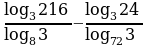
Решение. 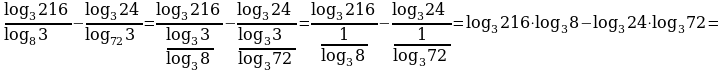
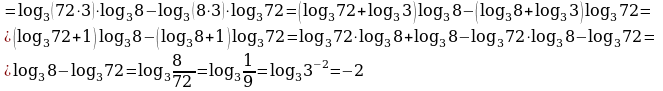
Пример 5. Упростить выражение 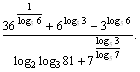
Решение. Преобразуем каждое слагаемое отдельно. При этом сделаем ссылку на конкретные свойства логарифмов, приведенные выше.
 |используем свойство 9|
|используем свойство 9|  |по свойству 5|=
|по свойству 5|= 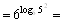 |по основному логарифмическому тождеству|
|по основному логарифмическому тождеству| 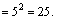
 |по свойству 10|
|по свойству 10| 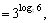
Тогда 
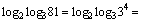 |по свойству 5| =
|по свойству 5| = 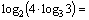
= |по свойству 2| = 
 |по свойству 8|
|по свойству 8| 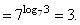
Таким образом:

З а м е ч а н и е 3. Решение этого примера при одновременном преобразовании всех слагаемых (что и следует делать) выглядит так:

Пример 6. Вычислить 
Решение. Для преобразования первого и второго слагаемых используем формулу изменения основания логарифма (свойство 9), а затем свойства 3 и 5.
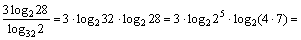
= |по свойствам 5 и 2| =

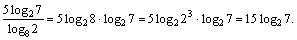
Для преобразования третьего слагаемого используем свойства 3–5:
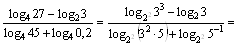


Тогда получаем:

З а м е ч а н и е 4. Подробное описание решения и преобразование всех слагаемых отдельно приведено исходя из соображений доступности объяснений. Целесообразно делать преобразования всего выражения сразу, аналогично тому, как сделано в замечании
Пример 7. Прологарифмировать по основанию 10 выражение

Решение. Замечаем, что сделать это можно, если 
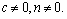 Тогда
Тогда
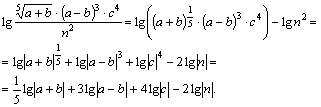
Пример 8. Выполнить потенцирование выражения
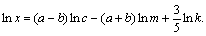
Решение. Используем свойства логарифмов 3–5 («справа–налево»):

Получаем ответ: 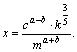
Пример 9. Выразить 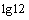 через
через  и
и 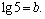
Решение. 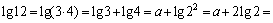

Выполните следующие задания
1 вариант 2 вариант
Вычислить:
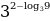
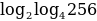
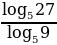
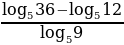
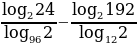
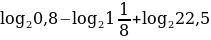
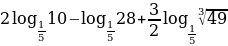
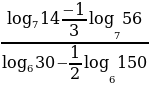 (*)
(*)
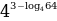
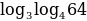
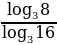
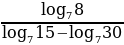
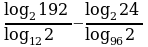
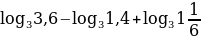
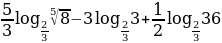
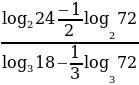 (*)
(*)
Порядок выполнения работы
При выполнении практической работы надо придерживаться следующих правил:
1.Практическую работу следует выполнять в тетради, синей или черной шариковой ручкой, оставляя поля.
2.На обложке тетради должны быть ясно написаны название дисциплины, фамилия, инициалы студента, номер группы.
3. В заголовке работы должны быть указаны номер практической работы, тема практической работы, номер варианта.
4.Перед решением каждого задания надо выписать полное условие.
5.Решение заданий следует излагать подробно и аккуратно, объясняя и мотивируя все действия решения.
6. После получения проверенной работы, студент должен исправить все отмеченные ошибки.
Пояснение и рекомендации к выполнению работы.
Содержание отчета:
1. Наименование работы, номер работы, вариант.
2. Цель работы.
3. Оборудование, используемое для выполнения практической работы.
4. По необходимости краткая теория.
5. Номер задания и его условие.
6. Последовательность выполнения работы, необходимые решения.
7.Ответы на контрольные вопросы.
8. Выводы о проделанной работе.
9.Используемая литература: перечень справочной литературы, таблиц
Контрольные вопросы.
Логарифма числа. Понятие.
Основное логарифмическое тождество.
Десятичного логарифма числа. Понятие.
Натурального логарифма числа. Понятие
Основные свойства логарифмов.
Формула перехода от логарифма по одному основанию к логарифму по другому основанию.
Рекомендуемая литература
Башмаков, М.И. Алгебра и начала анализа 10 кл. Базовый уровень : учебник для общеобразоват. учреждений - М.: Дрофа, 2014.-288 с.
Башмаков М.И. Математика: учебник для учреждений нач. и сред. проф. образования. – М.: Издательский центр «Академия», 2012.-256 с.
Башмаков М.И. Алгебра и начала анализа 11 кл. Базовый уровень: учебник для общеобразоват .учреждений- М: Издательский центр «Академия»», 2010.-288с.
Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В. Математика: алгебра и начала математического анализа, геометрия 10 класс, учеб. для общеобразоват. организаций: базовый и углубл. уровни -М.: Просвещение,2014.-431с
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ
ПРАКТИЧЕСКОЙ РАБОТЫ № 5
Учебная дисциплина: «МАТЕМАТИКА:
АЛГЕБРА И НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА; ГЕОМЕТРИЯ»
№ 2.3 Тема: ««Логарифмические уравнения, и методы их решения»».
Цель занятия: Обобщение свойств логарифмов, применение их к решению уравнений;
Закрепление основных методов решения логарифмических уравнений
Оборудование: методическое указание к выполнению практической работы, лекции, учебная литература, тетрадь для оформления практических работ.
Норма времени: 225 мин.
Теоретические сведения
Примеры и последовательность выполнения заданий.
Простейшее логарифмическое уравнение:
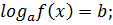
ОДЗ: 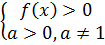
Решение:
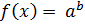 ;
;
Отбор корней, удовлетворяющих ОДЗ.
Пример:
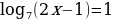
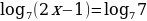
2х-1=7 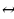 2х=8
2х=8 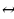 х=4
х=4
Проверка: 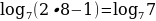 =1
=1
1=1
Ответ: х=4.
По свойству логарифмов и определение логарифма
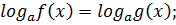
ОДЗ: 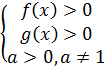
1)Решить f(x)=g(x)
2)Отбор корней, удовлетворяющих ОДЗ.
Пример:
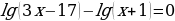
ОДЗ:
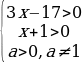 ;
; 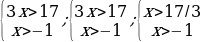 x
x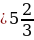 .
.
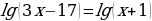
3x-17=x+1
3x-x=17+1
2x=18
x=9 - уд. ОДЗ
Ответ: х=9
Замечание: Можно решить без ОДЗ, но тогда обязательна проверка!
3.Если в уравнении логарифмы с разными основаниями
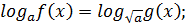
ОДЗ: 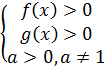
1)Сведите логарифмы к одному основанию
2)Отбор корней, удовлетворяющих ОДЗ.
Пример 1:
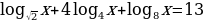
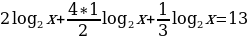
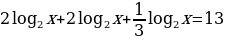
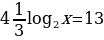
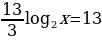 ,
, 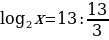
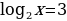 , х=23 , х=8
, х=23 , х=8
Ответ: х=8.
4.Метод введения новой переменной
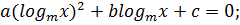
ОДЗ: 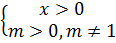
Пусть 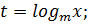 at2+bt+c=0
at2+bt+c=0
Решим квадратное уравнение
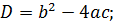
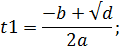
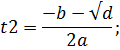
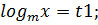
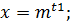
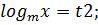
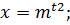
Пимер 1:
log22x+2log2x-3=0
ОДЗ: х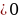
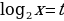 , t
, t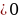
t2+2t-3=0 t1=1 , t2=-3 –посторонний корень, т.к. t 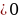
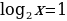 ,
,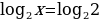 , x=2
, x=2
Ответ: х=2.
Пример 2: (разные основания и ввод новой переменной)
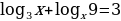
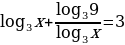 /*
/*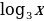
log 32x+log39=3log3x
log 32x+2=3log3x
log 32x -3log3x+2=0
log3x=t , t2-3t+2=0 , t1=2, t2=1
log3x=t1 , log3x=2, log3x=log39, x=9
log3x=t2, log3x=1, log3x= log33, x=3
Ответ: 9;3.
Выполните следующие задания
1 вариант 2 вариант
Решите уравнения:
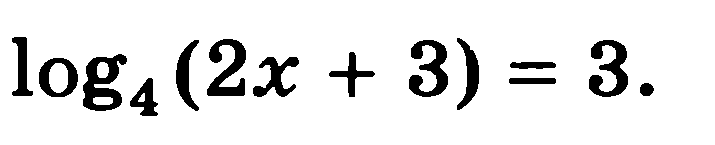
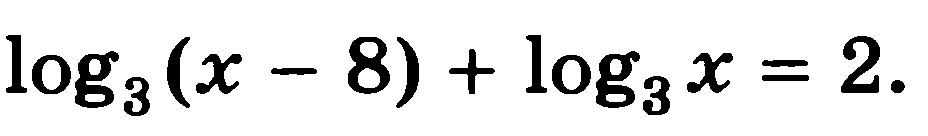

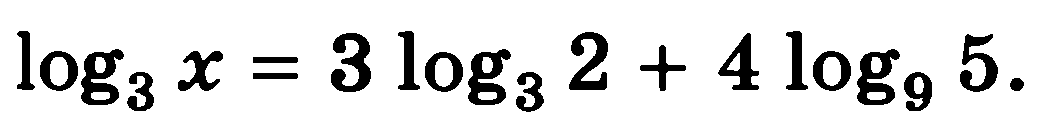

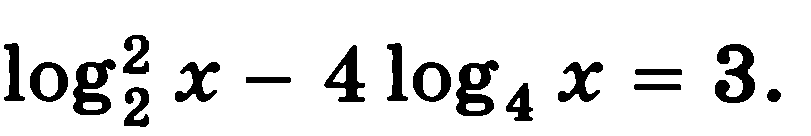
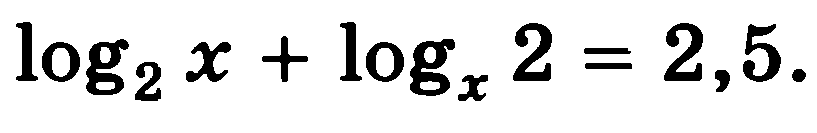
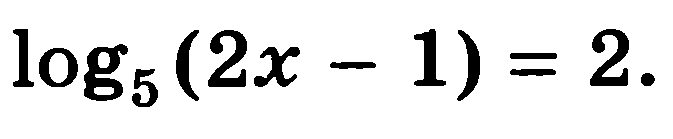
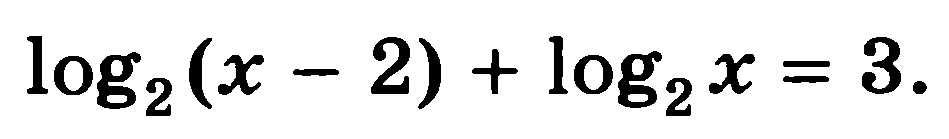

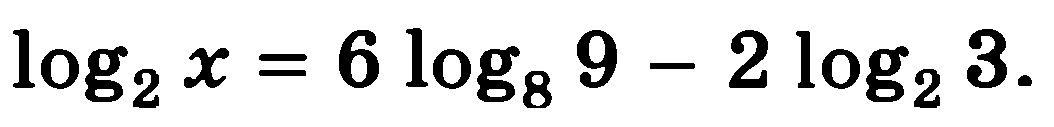
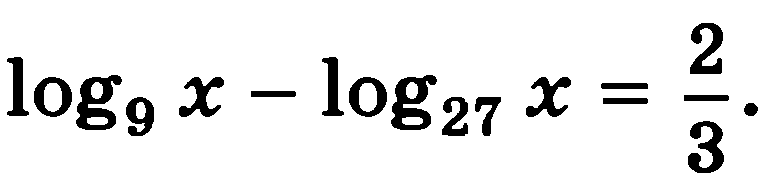

7) 
Порядок выполнения работы
При выполнении практической работы надо придерживаться следующих правил:
1.Практическую работу следует выполнять в тетради, синей или черной шариковой ручкой, оставляя поля.
2.На обложке тетради должны быть ясно написаны название дисциплины, фамилия, инициалы студента, номер группы.
3. В заголовке работы должны быть указаны номер практической работы, тема практической работы, номер варианта.
4.Перед решением каждого задания надо выписать полное условие.
5.Решение заданий следует излагать подробно и аккуратно, объясняя и мотивируя все действия решения.
6. После получения проверенной работы, студент должен исправить все отмеченные ошибки.
Пояснение и рекомендации к выполнению работы.
Содержание отчета:
1. Наименование работы, номер работы, вариант.
2. Цель работы.
3. Оборудование, используемое для выполнения практической работы.
4. По необходимости краткая теория.
5. Номер задания и его условие.
6. Последовательность выполнения работы, необходимые решения.
7.Ответы на контрольные вопросы.
8. Выводы о проделанной работе.
9.Используемая литература: перечень справочной литературы, таблиц
Контрольные вопросы.
Что понимают под логарифмическим уравнением?
Что называется корнем уравнения?
Что значит «решить уравнение»?
Какие уравнения называются равносильными?
Что такое потенцирование?
Обязательной ли является в общем случае проверка найденных значений неизвестного по условию уравнения?
Какие свойства логарифмов вам известны?
Рекомендуемая литература
Башмаков, М.И. Алгебра и начала анализа 10 кл. Базовый уровень : учебник для общеобразоват. учреждений - М.: Дрофа, 2014.-288 с.
Башмаков М.И. Математика: учебник для учреждений нач. и сред. проф. образования. – М.: Издательский центр «Академия», 2012.-256 с.
Башмаков М.И. Алгебра и начала анализа 11 кл. Базовый уровень: учебник для общеобразоват .учреждений- М: Издательский центр «Академия»», 2010.-288с.
Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В. Математика: алгебра и начала математического анализа, геометрия 10 класс, учеб. для общеобразоват. организаций: базовый и углубл. уровни -М.: Просвещение,2014.-431с
6.Перечень литературы и средств обучения
Башмаков, М.И. Алгебра и начала анализа 10 кл. Базовый уровень : учебник для общеобразоват. учреждений - М.: Дрофа, 2014.-288 с.
Башмаков М.И. Математика: учебник для учреждений нач. и сред. проф. образования. – М.: Издательский центр «Академия», 2012.-256 с.
Башмаков М.И. Алгебра и начала анализа 11 кл. Базовый уровень: учебник для общеобразоват. Учреждений - М: Издательский центр «Академия»», 2010.-288с.
Башмаков М.И. Математика. Практикум по решению задач.10-11классы-М.: Просвещение,2009.-223с.
Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В. Математика: алгебра и начала математического анализа, геометрия 10 класс, учеб. для общеобразоват. организаций: базовый и углубл. уровни -М.: Просвещение,2014.-431с
Зайцева Н.Н. «Разработка и экспертиза комплексного учебно-методического обеспечения ФГОС профессионального образования: комплекс справочных и оценочных материалов. Методические рекомендации», Волгоград: Изд-во ВГАПО,2015.-64с.
Хованскова Т. А., «Сборник методических указаний по выполнению практических работ», преподаватель ГБОУ СПО «Донецкий сельскохозяйственный техникум», Миллерово, 2015 г.
Дорофеев Г.В., Потапов М.К., Розов Н.Х. « Математика: Для поступающих в вузы», Пособие,2002.-672с
Козко А.И., Макаров Ю.Н., Чирский В.Г., «Математика письменный экзамен Решение задач. Методы и идеи», Учебное пособие. М: Издательство «Экзамен», 2007-511с.
Карп А.П., «Сборник задач по алгебре и началам анализа», Учебное пособие. М: Просвещение, 2006-176с.
Садовничий Ю.В. «Алгебра конкурсные задачи с решениями», Учебное пособие. М: Издательство «Экзамен»,2007.-445с.
8.Контроль и оценка результатов освоения дисциплины
Критериями оценки результатов работы являются:
уровень усвоения учебного материала;
умение использовать теоретического знания при выполнении практических задач;
Сформированность общеучебных компетенций;
Обоснованность и четкость изложения материала;
Уровень оформления работы
Анализ результатов
Практическая работа выполнена в полном объёме и правильно, оформлена, то ставиться оценка –«отлично».
Практическая работа выполнена более чем на 75%, ставиться оценка «хорошо».
Практическая работа выполнена более чем на 60%, ставиться оценка «удовлетворительно»
В противном случае работа не засчитывается.
36







 0,1 , в=3,4
0,1 , в=3,4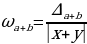 =
= 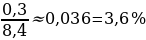
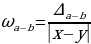 =
=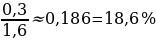
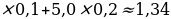
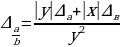 =
=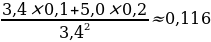
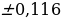 .
.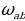 =
=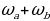 =
=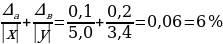
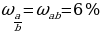
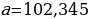 ,
, 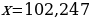
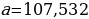 ,
, 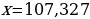


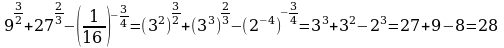
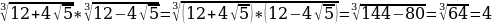
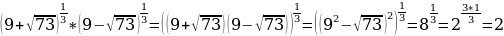

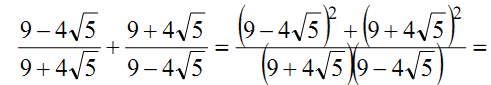
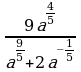 при а = 5
при а = 5
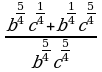 при b=2, c=5
при b=2, c=5
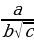 Решение
Решение 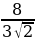 Решение
Решение 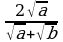 Решение
Решение 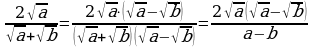 .
.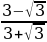 Решение:
Решение: 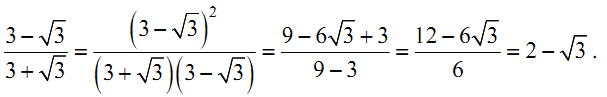
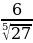 Решение:
Решение: 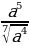 Решение :
Решение : 
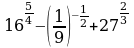 .
. 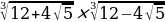 ;
;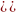 ;
;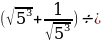 ) ;
) ;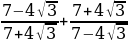 .
.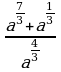 при а = 2
при а = 2 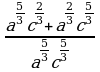 при а=7, с=3
при а=7, с=3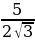 ; б)
; б) 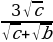 ; в)
; в) 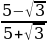 ;
;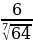 д)
д) 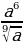
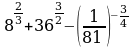 .
.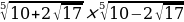 ;
;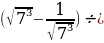 ) ;
) ;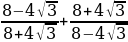 .
.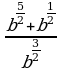 при b=3
при b=3 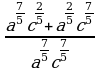 при а=9, с=2
при а=9, с=2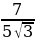 ; б)
; б) 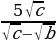 ; в)
; в) 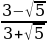 ;
;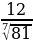 д)
д) 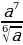
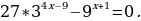
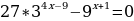
 3x
3x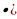 1-35)=0
1-35)=0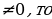
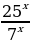 =1
=1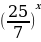 =1
=1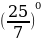 x=0 Ответ: 0.
x=0 Ответ: 0.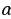 f(x) = t, t0 преобразуются к квадратным уравнениям (или к уравнениям более высоких степеней).
f(x) = t, t0 преобразуются к квадратным уравнениям (или к уравнениям более высоких степеней).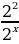 = 15
= 15 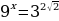
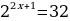
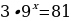
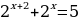
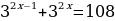
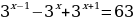
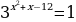
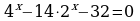
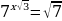
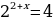
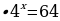
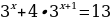
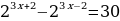
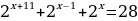
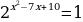
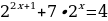
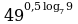
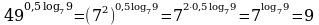
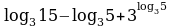
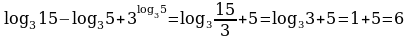
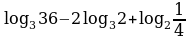
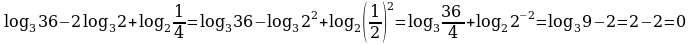 Пример 3. Упростить выражение.
Пример 3. Упростить выражение. 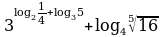
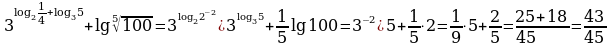
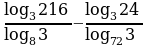
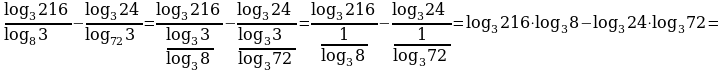
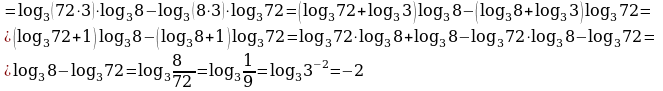
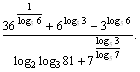





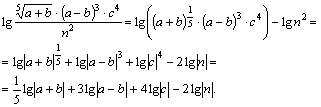

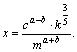

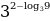
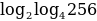
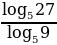
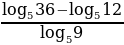
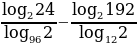
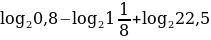
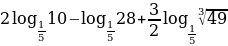
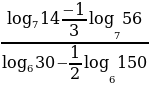 (*)
(*)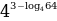
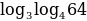
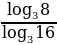
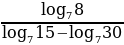
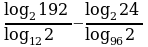
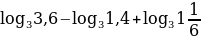
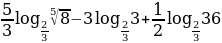
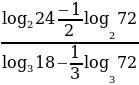 (*)
(*)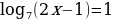
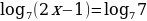
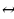 2х=8
2х=8 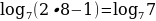 =1
=1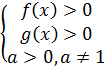
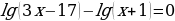
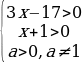 ;
; 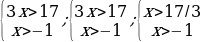 x
x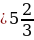 .
.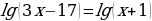
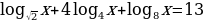
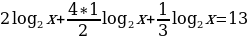
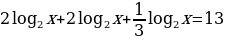
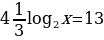
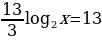 ,
, 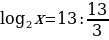
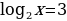 , х=23 , х=8
, х=23 , х=8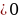
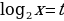 , t
, t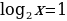 ,
,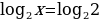 , x=2
, x=2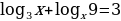
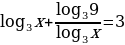 /*
/*