Учитель математики Малова Вера Михайловна
МБУ «Школа № 2 имени героя социалистического труда И.В. Комзина»
г. Тольятти Самарской области
Малова В.М.
«Квадратные уравнения», 2016, 27 с.
В методическом пособии «Квадратные уравнения» представлены пояснительная записка, краткие теоретические сведения, решение уравнений, дидактический материал, список литературы.
Методическое пособие по разделу математики «Квадратные уравнения» можно использовать при подготовке к экзаменам, на дополнительных занятиях и при самостоятельном изучении. Примеры подобраны с различной степенью трудности: от простых до достаточно сложных и требующих нетрадиционных методов их решения. Данное пособие может не только помочь пополнить, систематизировать, углубить знания по алгебре, но и способствовать формированию умений применять приемы сравнения, выделения главного, переноса знаний в новую ситуацию; развитию творческих способностей учащихся путем решения заданий более сложного уровня.
Пояснительная записка
Тема «Квадратные уравнения» очень важна для изучения курса математики средней школы, т. к. является ступенькой в изучении более сложного материала математики средней школы. Умение быстро, рационально и правильно решать квадратные уравнения облегчает прохождение многих тем курса математики. Например, при изучении следующих тем:
8-й класс – решение задач на составление квадратных уравнений;
9-й класс – разложение квадратного трехчлена на множители; квадратичная функция и ее график; неравенства второй степени с одной переменной;
10-й класс – тригонометрические уравнения и неравенства; применение производной к исследованию функции;
11-й класс – интеграл; площадь криволинейной трапеции; иррациональные уравнения; показательные уравнения и неравенства; логарифмические уравнения и неравенства.
Цель работы:
Помочь всем желающим пополнить, систематизировать, углубить свои знания по решению квадратных уравнений.
В школьном курсе математики изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые уравнения. Однако имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать многие уравнения.
В работе рассматриваются различные способы решения квадратных уравнений:
- разложение левой части уравнения на множители;
- метод выделения полного квадрата;
- решение квадратных уравнений по формуле;
- решение уравнений с использованием теоремы Виета;
- решение уравнений способом «переброски»;
- свойства коэффициентов квадратного уравнения.
Методическое пособие по разделу математики «Квадратные уравнения» можно использовать при подготовке к экзаменам, на дополнительных занятиях и при самостоятельном изучении.
В пособии даются краткие теоретические сведения, решение уравнений. Примеры подобраны с различной степенью трудности: от простых до достаточно сложных и требующих нетрадиционных методов их решения. В принципе это краткий математический справочник, который поможет ученику самостоятельно и глубоко изучить тему «Квадратные уравнения и способы их решения».
Данное пособие может не только помочь пополнить, систематизировать, углубить знания по алгебре, но и способствовать формированию умений применять приемы сравнения, выделения главного, переноса знаний в новую ситуацию; развитию творческих способностей учащихся путем решения заданий более сложного уровня.
Основные понятия
Квадратным уравнением называется уравнение, левая часть которого есть многочлен стандартного вида второй степени относительно  , а правая – нуль.
, а правая – нуль.
Квадратное уравнение называют также уравнением второй степени.
Уравнения 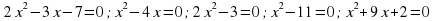
могут служить примерами квадратных уравнений.
Общее квадратное уравнение — это уравнение вида
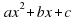 = 0, (1)
= 0, (1)
где коэффициенты a, b и с — произвольные числа, причем a ≠ 0. Число a называется коэффициентом при 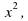 число b - коэффициентом при
число b - коэффициентом при  , число с свободным членом уравнения (1). Так, в уравнении
, число с свободным членом уравнения (1). Так, в уравнении
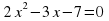
2 - коэффициент при 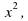 (- 3) - коэффициент при
(- 3) - коэффициент при  , (- 7) - свободный член; в уравнении
, (- 7) - свободный член; в уравнении
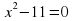
1 - коэффициент при 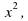 0 - коэффициент при
0 - коэффициент при  , (- 11) - свободный член.
, (- 11) - свободный член.
Корнями квадратного уравнения называются значения переменной, при которых уравнение обращается в верное числовое равенство.
Например, число 0 является корнем уравнения
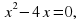
Ибо если подставить 0 вместо х, то получим верное числовое равенство
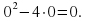
Решить квадратное уравнение – это значит найти все его корни или установить, что корней нет.
При решении квадратных уравнений нам придется умножать или делить обе части уравнения на не равное нулю число, а также переносить члены из одной части уравнения в другую. В результате будет получаться уравнение, равносильное прежнему, т.е. уравнение, имеющее те же корни, что и прежнее уравнение.
Квадратное уравнение может иметь два, один или ни одного корня. Чтобы определить, сколько корней имеет квадратное уравнение, необходимо найти дискриминант квадратного уравнения D =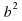 − 4ac.
− 4ac.
Если D , то уравнение не имеет корней.
Если D = 0, то уравнение имеет ровно один корень.
Если D 0, то уравнение имеет два корня.
Корни квадратного уравнения можно найти по формуле:
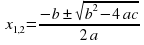 .
.
Если второй коэффициент b равен четному числу, то корни квадратного уравнения можно найти по формуле:
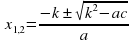 , где
, где 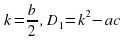 .
.
Если первый коэффициент a равен единице, то уравнение называется приведенным.
Уравнения
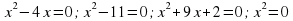
могут служить примерами приведенных квадратных уравнений.
Приведенное квадратное уравнение в общем виде обычно записывают следующим образом:
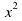 + px + q = 0 , (2)
+ px + q = 0 , (2)
где p и q – заданные числа. Число p есть коэффициент при , а q – свободный член.
, а q – свободный член.
Таким образом, уравнение (2) можно рассматривать как частный случай общего квадратного уравнения (1), где a, = 1, b = p и с = q.
Дискриминант уравнения (2) равен
D =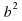 − 4ac =
− 4ac = 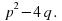 (3)
(3)
Пусть D 0. Тогда, как мы знаем, уравнение (2) имеет два корня, которые вычисляются по формуле: 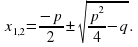
При D = 0 по этой формуле вычисляют также совпадающие корни. Именно, в этом случае
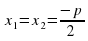 .
.
Если же D то уравнение (2) не имеет корней.
Обычно в случае приведенного уравнения (2) вместо дискриминанта D рассматривают выражение 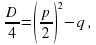 имеющее тот же знак, что и D.
имеющее тот же знак, что и D.
Если b = 0 или с = 0, то квадратное уравнение называется неполным. Неполное квадратное уравнение удобно решать, разложив на множители левую часть уравнения.
Неполное квадратное уравнение, у которого  = 0, имеет вид
= 0, имеет вид
a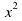 + c = 0, (а
+ c = 0, (а (4)
(4)
Это уравнение равносильно уравнению
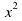 +
+  (5)
(5)
Ясно, что если  есть число положительное, то уравнение (5) будет равносильно уравнению
есть число положительное, то уравнение (5) будет равносильно уравнению
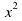 =
=  . (6)
. (6)
Так как число ( положительно, то
положительно, то
 =
=  .
.
Следовательно, уравнение (6), а значит, и уравнение (4) имеют два корня:
 и
и  ,
,
и других корней не имеют.
С квадратным уравнением связана теорема Виета.
Прямая теорема Виета утверждает: если у квадратного уравнения 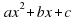 = 0 есть корни
= 0 есть корни  , выполняются соотношения:
, выполняются соотношения:
Иногда с помощью обратной теоремы Виета удобно находить корни квадратного уравнения. Обратная теорема Виета утверждает: если для некоторых постоянных a, b и с
существуют числа  , удовлетворяющих соотношениям:
, удовлетворяющих соотношениям:
то эти числа  являются корнями уравнения
являются корнями уравнения
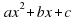 = 0.
= 0.
Биквадратное уравнение – уравнение вида
 , (7)
, (7)
где a, b и с – данные числа и а
Чтобы решить уравнение (7), вводят новое неизвестное при помощи равенства
 , где
, где  (8)
(8)
Тогда уравнение (7) превращается в квадратное уравнение
 (9)
(9)
относительно неизвестного  .
.
Если уравнение (9) не имеет корней, то, очевидно, и данное уравнение (7) не имеет корней.
Если же уравнение (9) имеет корни, то, подставив их в равенство (8), вместо  , получим уравнения относительно х. Решения полученных уравнений, если они существуют, и являются решениями уравнения (7). Других решений уравнение (7), очевидно, не имеет.
, получим уравнения относительно х. Решения полученных уравнений, если они существуют, и являются решениями уравнения (7). Других решений уравнение (7), очевидно, не имеет.
Дробное уравнение - уравнение вида - некоторые многочлены. Дробное уравнение равносильно системе:
Решение дробного уравнения можно разбить на два этапа:
решить уравнение p( ) = 0;
) = 0;
проверить условие q( )
) 
Квадратный трехчлен – многочлен второй степени с одной переменной 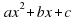 , где
, где  , b – коэффициенты, с – свободный член,
, b – коэффициенты, с – свободный член, 
Корнями квадратного трехчлена являются значения переменной, при которых значение квадратного трехчлена равно нулю.
Если  - корни квадратного трехчлена, то его можно разложить на множители следующим способом:
- корни квадратного трехчлена, то его можно разложить на множители следующим способом:
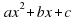 =
= 
Система уравнений второй степени – система, состоящая из двух уравнений второй степени или из одного уравнения первой степени, а другого - второй степени. При решении уравнений второй степени используются способ подстановки, способ сложения, графический способ, способ введения новых переменных.
Способ введения новых переменных заключается в том, что вводится новая переменная только в одно уравнение или две новые переменные сразу для обоих уравнений, далее уравнение или уравнения решаются относительно новых переменных, после этого остается уже решить более простую систему уравнений, из которой находят искомое решение.
| Квадратное уравнение | Корни квадратного уравнения |
|
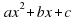 = 0 = 0
| Формула корней | Свойства корней (теорема Виета) |
| | 
|
| Приведенное квадратное уравнение (а = 1) 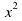 + px + q = 0 + px + q = 0
| |

|
| Уравнение с четным вторым коэффициентом (b = 2k) a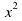 + 2kx + c = 0 + 2kx + c = 0 | 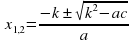
| |
Решение квадратных уравнений
Пример 1. Решить квадратное уравнение:
а) 
Решение:
a = 1, b = - 1 и с = - 12
Вычисляем дискриминант уравнения:
D =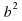 − 4ac =
− 4ac =
Значит, это уравнение имеет два корня, которые вычисляются по формуле
Итак, уравнение имеет два корня:  = 4,
= 4, 
Ответ:  4.
4.
б) 
Решение:
a = 3, b = 2 и с = - 2
Вычисляем дискриминант уравнения:
D =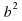 − 4ac =
− 4ac =
Значит, это уравнение имеет два корня, которые вычисляются по формуле
Итак, уравнение имеет два корня:  =
=  ,
, 
Ответ:  ,
, 
в) 
Решение:
Вычисляем дискриминант уравнения:
D =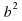 − 4ac = .
− 4ac = .
Значит, уравнение не имеет корней.
Ответ: нет корней.
г) 
Решение:
a = 25, b = - 30 и с = 9
Вычисляем дискриминант уравнения:
D =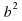 − 4ac = 0.
− 4ac = 0.
Значит, это уравнение имеет единственный корень, который можно вычислить по формуле
Итак, уравнение имеет единственный корень  , или, что все равно два совпадающих корня:
, или, что все равно два совпадающих корня:
Ответ: 0,6
д) 
Решение:
Второй коэффициент в уравнении является четным числом. Найдем дискриминант для четного второго коэффициента:
 .
.
Уравнение имеет два корня:
; 
Ответ: 0,5; 1,5.
Пример 2. Решить неполное квадратное уравнение:
а)  - 1 = 0.
- 1 = 0.
Решение:
Способ 1. Решим данное уравнение, разложив на множители выражение  – 1:
– 1:
 – 1 = (2
– 1 = (2 – 1)(2
– 1)(2 + 1).
+ 1).
Получим уравнение:
(2 – 1)(2
– 1)(2 + 1) = 0.
+ 1) = 0.
Произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, а другой при этом не теряет смысл.
2 – 1 = 0 или 2
– 1 = 0 или 2 + 1 = 0
+ 1 = 0
 = 0,5 или
= 0,5 или  = - 0,5
= - 0,5
Способ 2.
 - 1 = 0
- 1 = 0
Перенеся свободный член в правую часть, получим уравнение
 = 1,
= 1,
равносильное данному.
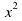 =
= 
 = -
= -  или
или =
= 
 = - 0,5 или
= - 0,5 или  = 0,5
= 0,5
Ответ: - 0,5; 0,5.
б) 
Решение:
Решим данное уравнение, разложив на множители выражение 
 =
=  (
( + 3).
+ 3).
Получим равносильное уравнение:
 (
( + 3) = 0.
+ 3) = 0.
Следовательно,  = 0 или
= 0 или  = - 3.
= - 3.
Ответ: - 3; 0.
в) 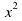 + 7 = 0
+ 7 = 0
Решение:
Рассмотрим выражение, стоящее в левой части уравнения.
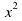
 0 при любом значении х, следовательно,
0 при любом значении х, следовательно, 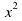 + 7
+ 7  0 при любом значении х.
0 при любом значении х.
Можно сделать вывод, что данное уравнение не имеет решений.
Ответ: нет решений.
в) 
Решение:
Мы знаем, что существует только одно число – нуль, квадрат которого равен нулю. Следовательно, уравнение имеет единственный корень  = 0.
= 0.
Ответ:  = 0.
= 0.
г) 
Решение:
Это уравнение равносильно уравнению 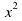 = 5.
= 5.
Следовательно, нам надо найти числа, квадраты которых равны числу 5; таких чисел только два:  и
и  .
.
Таким образом, уравнение имеет два корня:  и других корней не имеет.
и других корней не имеет.
Ответ: 

Пример 3. Решить приведенное квадратное уравнение:
а) 
Решение:
a = 1, b = p = - 8 и с = 7
Вычисляем = 
 = 4
= 4 
 = 4
= 4 
Следовательно, уравнение имеет два корня: 
Ответ: 1; 7.
б) 
Решение:
a = 1, b = p = - 4 и с = 3
Вычисляем = 
 =
= 
Следовательно, уравнение имеет два корня: 
Ответ: 1; 3.
Пример 4. Решить биквадратное уравнение:
а) 
Решение:
Уравнение после замены , где
, где  превращается в квадратное уравнение
превращается в квадратное уравнение
 .
.
Его дискриминант D =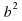 − 4ac =
− 4ac =
И, следовательно, оно имеет два корня:
 , т.е
, т.е  .
.
Подставляя эти числа вместо  в равенство
в равенство  , получим уравнение относительно
, получим уравнение относительно  :
:
 и
и 
Решая их получим четыре корня уравнения: 
Других корней уравнение не имеет.
Ответ: 
б) 
Решение:
Уравнение после замены , где
, где  превращается в квадратное уравнение
превращается в квадратное уравнение
 .
.
Его дискриминант D =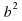 − 4ac =
− 4ac =
и, следовательно, оно имеет два корня:
, т.е  .
.
Подставляя эти числа вместо  в равенство
в равенство  , получим уравнение относительно
, получим уравнение относительно  :
:
,

Подставляя не имеющее корней, потому что 
Таким образом, уравнение имеет два найденных выше корня  и других корней не имеет.
и других корней не имеет.
Ответ: 
в) 
Решение:
Уравнение после замены , где
, где  превращается в квадратное уравнение
превращается в квадратное уравнение
 .
.
Его дискриминант D =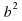 − 4ac =
− 4ac =
Следовательно, оно не имеет корней. Но тогда и исходное уравнение не имеет корней.
г) 
Решение:
Уравнение после замены , где
, где  превращается в квадратное уравнение
превращается в квадратное уравнение
 .
.
Его дискриминант D =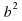 − 4ac =
− 4ac =
Оно имеет единственный корень
Подставляя  вместо
вместо  в равенство
в равенство  , получим уравнение относительно
, получим уравнение относительно  :
:

Решая его, получим два корня уравнения: 
Других корней уравнение не имеет.
Ответ: 

д) 
Решение:
Уравнение после замены , где
, где  превращается в квадратное уравнение
превращается в квадратное уравнение
 .
.
Его дискриминант D =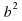 − 4ac =
− 4ac =
Оно имеет единственный корень
Подставляя  вместо
вместо  в равенство
в равенство  , получим уравнение относительно
, получим уравнение относительно  :
:

которое не имеет корней. Значит, исходное уравнение также не имеет корней.
Ответ: корней нет.
Пример 5. Решить рациональное уравнение:
а) 
Решение:
Мы знаем, что корнем уравнения относительно неизвестной  называется число
называется число  , при подстановке которого вместо
, при подстановке которого вместо  получается верное числовое равенство. Поэтому, если
получается верное числовое равенство. Поэтому, если  - корень исходного уравнения, то выражение
- корень исходного уравнения, то выражение  есть числовое выражение, равное нулю. Но тогда знаменатель этого выражения не должен равняться нулю, а числитель должен равняться нулю.
есть числовое выражение, равное нулю. Но тогда знаменатель этого выражения не должен равняться нулю, а числитель должен равняться нулю.
Таким образом, чтобы решить исходное уравнение, мы должны найти корни уравнения 
и подставить их в знаменатель левой части исходного уравнения. Те из них, которые не обращают знаменатель в нуль, являются корнями исходного уравнения. Других корней уравнение не имеет.
Дискриминант исходного уравнения
D =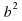 − 4ac =
− 4ac =
и, следовательно, оно имеет два корня:
,
т.е. 
Подставляя эти числа в знаменатель левой части уравнения, получаем:
если  то
то 
если  то
то
Это показывает, что числа

являются корнями исходного уравнения, и других корней уравнение не имеет.
Ответ: - 7, 3.
б) 
Решение:
Рассуждая как в предыдущем примере, решим сначала уравнение

Оно имеет два корня:

Подставляя эти числа в знаменатель левой части уравнения, получаем:
если  то
то
если  то
то
Следовательно, исходное уравнение имеет единственный корень 
Ответ: 2.
в)
Решение:
Решим сначала уравнение 
Оно имеет единственный корень  = 1,5.
= 1,5.
Так как  = то исходное уравнение не имеет корней.
= то исходное уравнение не имеет корней.
Ответ: нет корней.
г) 
Решение:
Данное уравнение не имеет корней, потому что уравнение

не имеет корней.
Ответ: нет корней.
д) 
Решение:
Левая часть этого уравнения определена на множестве всех действительных чисел, кроме  Следовательно, и корни этого уравнения надо искать только среди этих значений
Следовательно, и корни этого уравнения надо искать только среди этих значений 
Выполним преобразования левой части уравнения:
Таким образом, мы преобразовали заданное уравнение к виду

Решим сначала уравнение  Оно имеет единственный корень
Оно имеет единственный корень  При этом число
При этом число  не обращает в нуль знаменатель дроби левой части исходного уравнения:
не обращает в нуль знаменатель дроби левой части исходного уравнения:

Значит, исходное уравнение имеет единственный корень 
Ответ: 3.
е) 
Решение:
Перенеся правую часть данного уравнения налево, получим уравнение

равносильное исходному.
Применим к левой части уравнения правила сложения и вычитания алгебраических дробей:
.
Рассуждая, как в предыдущем примере, получим, что исходное уравнение равносильно уравнению
Решим сначала уравнение 
Поскольку его дискриминант D =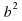 − 4ac = то оно не имеет корней.
− 4ac = то оно не имеет корней.
Значит, исходное уравнение так же не имеет корней.
Ответ: нет корней.
Пример 6. Составить квадратное уравнение, корнями которого являются числа
Решение:
Согласно теореме Виета, если у квадратного уравнения 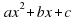 = 0 есть корни
= 0 есть корни  то выполняются соотношения
то выполняются соотношения

В нашем случае 
 = =
= =
= 
Искомое уравнение:  или
или  .
.
Ответ: 
Пример 7. При каких значениях  уравнение имеет два равных корня:
уравнение имеет два равных корня:
а) 
Решение:
Уравнение имеет два равных корня, когда дискриминант равен нулю. Найдем дискриминант данного уравнения:
D =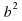 − 4ac =
− 4ac = 
D = 0; 

Значит, при  уравнение
уравнение  имеет два равных корня.
имеет два равных корня.
Ответ: 6,25.
б) 
Решение:
Уравнение имеет два равных корня, когда дискриминант равен нулю. Найдем дискриминант данного уравнения:
D =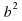 − 4ac =
− 4ac = 
Из уравнения  находим:
находим:  =
=  ;
; 
Значит, при  уравнение
уравнение  имеет два равных корня.
имеет два равных корня.
Ответ: - 4; 4.
Пример 8. Разложить на множители квадратный трехчлен:
а) 
Решение:
Для того чтобы разложить квадратный трехчлен на множители, необходимо найти его корни, если они существуют. Решим уравнение 
Второй коэффициент в уравнении является четным числом. Найдем дискриминант для четного второго коэффициента:
 .
.
Уравнение имеет два корня:
; 
Разложим многочлен  на множители:
на множители:
Ответ: 
б) 
Решение:
Решим уравнение 
Дискриминант данного уравнения равен нулю, значит, уравнение имеет два равных корня:

Разложим многочлен  на множители:
на множители:
Ответ: 
в) 
Решение:
Найдем дискриминант данного трехчлена:

Так как дискриминант меньше нуля, то квадратный трехчлен не имеет корней. Такой квадратный трехчлен нельзя представить в виде произведения многочленов первой степени.
Ответ: нельзя разложить на множители.
Пример 9. Сократить дробь:
а) 
Решение:
Разложим на множители квадратные трехчлены, стоящие в числителе и знаменателе дроби:

 .
.
Дробь принимает вид:
Разделим числитель и знаменатель дроби на общий множитель  получим дробь
получим дробь  .
.
Сокращение данной дроби можно выполнить при условии, что  не будет принимать значение, равное
не будет принимать значение, равное 
Ответ:  .
.
б) 
Решение:
Разложим числитель и знаменатель на множители, используя формулу разложения квадратного трехчлена на множители и формулу разности квадратов:

Дробь принимает вид: 
Разделим числитель и знаменатель дроби на общий множитель  , получим дробь
, получим дробь 
Сокращение данной дроби можно выполнить при условии, что  не будет принимать значение, равное
не будет принимать значение, равное 
Ответ: 
в) 
Решение:
Введем новую переменную, обозначив 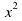 через t:
через t:  t.
t.
Получим рациональную дробь с переменной t:
 .
.
Разложим на множители квадратные трехчлены, стоящие в числителе и знаменателе получившейся дроби:

.
Разделим числитель и знаменатель дроби на общий множитель  , получим дробь
, получим дробь 
Вернемся к переменной  :
: 
Сокращение данной дроби можно выполнить при условии, что  , т.е.
, т.е. 
Ответ: 
Пример 10. Решить систему:
а)
Решение:
Решим систему способом подстановки. Выразим из второго уравнения переменную у:
у = 2
Подставим в первое уравнение системы вместо переменной у выражение 2 получим квадратное уравнение
получим квадратное уравнение  0.
0.
Из квадратного уравнения находим: 
Подставив полученные значения переменной  во второе уравнение, получим:
во второе уравнение, получим: 
Пары чисел ( являются решениями данной системы.
являются решениями данной системы.
Ответ: (
б)
Решение:
Введем новую переменную, обозначив  через z:
через z:
 z, тогда
z, тогда 
Первое уравнение системы принимает вид: z +  =
= 
Из этого уравнения находим: 
Тогда 
 другими словами, первое уравнение распалось на два уравнения.
другими словами, первое уравнение распалось на два уравнения.
Имеем две системы:
и
Решения этих систем являются решениями данной системы. Решением первой системы является пара чисел (2; 3), решением второй системы является пара чисел (3; 2).
Следовательно, решениями исходной системы
являются пары чисел (2; 3), (3; 2).
Рассмотренная система является симметричной системой уравнений, так как если вместо переменной  в уравнения подставить переменную у, а вместо переменной
в уравнения подставить переменную у, а вместо переменной  подставить переменную
подставить переменную  , то система не изменится.
, то система не изменится.
Ответ: (2; 3), (3; 2).
в)
Решение:
Раскроем скобки во втором уравнении системы:
Каждый член первого уравнения умножим на 2 и почленно сложим первое и второе уравнения, получим систему:
Выразим переменную  из первого уравнения:
из первого уравнения: 
Подставив во второе уравнение вместо переменной  выражение
выражение  , получим уравнение с одной переменной:
, получим уравнение с одной переменной:
2у · (4 + у) + 3(4 + у) – 3у = 6.
После преобразования уравнение принимает вид: 
Из этого уравнения находим: 
Подставив полученные значения переменной у в уравнение  , находим:
, находим:

Следовательно, решениями исходной системы являются пары чисел: (3;  (1;
(1; 
Ответ: (3;  (1;
(1; 
г)
Решение:
Преобразуем первое уравнение системы:


 = 4;
= 4;

Откуда 
Наша система распалась на две линейные системы:
 и
и 
Из системы  находим
находим 

Из системы  находим
находим 

Ответ: (4; 2), (2; 4).
Пример 11. Решить задачу:
а) Расстояние между пунктами А и В равно 78 км. Из пункта А выезжает велосипедист по направлению к В. Через один час ему навстречу отправляется из В другой велосипедист, проезжающий в час на 4 км больше первого. Встреча произошла на расстоянии 36 км от пункта В. Сколько времени до встречи ехал каждый из них и с какой скоростью?
Решение:
Пусть первый велосипедист ехал  часов, тогда второй велосипедист ехал (
часов, тогда второй велосипедист ехал ( До места встречи первый велосипедист проехал 78 – 36 = 42 (км), а второй – 36 км.
До места встречи первый велосипедист проехал 78 – 36 = 42 (км), а второй – 36 км.
Значит, скорость первого велосипедиста равна  второго –
второго –  . По условию задачи скорость второго велосипедиста больше скорости первого на 4 км/ч, поэтому можем составить следующее уравнение:
. По условию задачи скорость второго велосипедиста больше скорости первого на 4 км/ч, поэтому можем составить следующее уравнение: 
Решим уравнение:
Из уравнения  находим:
находим: 
Если  то
то 
 Значит, число
Значит, число  является корнем уравнения
является корнем уравнения

Если  то
то 
 Значит, число
Значит, число  является корнем уравнения
является корнем уравнения

Корень  не удовлетворяет условию задачи.
не удовлетворяет условию задачи.
Получили, что первый велосипедист ехал до встречи 3 часа, второй 3 – 1 = 2 (ч). Тогда скорость первого велосипедиста равна 42 : 3 = 14 (км/ч), а скорость второго велосипедиста равна 14 + 4 = 18 (км/ч).
Ответ: первый велосипедист ехал до встречи 3 часа со скоростью 14 км/ч, а второй – 2 часа со скоростью 18 км/ч.
б) Двое рабочих, работая вместе, выполнят некоторую работу за 8 часов. Первый из них, работая отдельно, может выполнить всю работу на 12 часов скорее, чем второй рабочий, если этот последний будет работать отдельно. За сколько часов каждый из них, работая отдельно, может выполнить работу?
Решение:
Примем объем работы, которую должны выполнить рабочие, за 1. Пусть первый выполнит всю работу за  часов, работая отдельно, тогда второму для выполнения этой работы необходимо (
часов, работая отдельно, тогда второму для выполнения этой работы необходимо ( + 12) часов.
+ 12) часов.
Получаем:
Так как двое рабочих, работая вместе, выполнят некоторую работу за 8 часов, то за один час они выполняют  всей работы. На основании этого составим следующее уравнение:
всей работы. На основании этого составим следующее уравнение:

Решим уравнение: 
После преобразований уравнение принимает вид:
Из уравнения  находим:
находим: 
Полученные корни являются корнями уравнения  , так как при
, так как при
 ,
, 
Но корень  не удовлетворяет условию задачи.
не удовлетворяет условию задачи.
Значит, первый рабочий может выполнить всю работу за 12 часов, работая один.
За 12 + 12 = 24 (ч) может выполнить всю работу второй рабочий, работая один.
Ответ: 12 ч, 24 ч.
Дидактический материал
I. Для заданных значений а b, с составьте квадратное уравнение:
b, с составьте квадратное уравнение:
а = 5, b = 2, с = -1.
а = 2, b = - 1 , с = - .
.
а = - 12, b = 0, с = - 0,1.
а = 0,75, b = - m, с = 1,2.
а = 5, b = 2, с = 0.
а = 5, b = 0, с = 0.
II. Приведите уравнение к виду: a + bx + c = 0
+ bx + c = 0
х (х + 2) = 3.
х (х – 7) = 5.
2х (х + 11) = 17.
(х – 2) (х + 2) = 3х.
3 (х + 1) (х – 1) = - х.
(х + 3) (х – 2) = 10.
III. Найдите число корней уравнения:
3 + x - 10 = 0.
+ x - 10 = 0.
4 + 4x + 1 = 0.
+ 4x + 1 = 0.
 + 6,25 = 0.
+ 6,25 = 0.
3 - 7x - 15 = 0.
- 7x - 15 = 0.
IV. Решите уравнение:
 - 6x + 8 = 0.
- 6x + 8 = 0.
 + 4 = 5х.
+ 4 = 5х.
х + 6 =  .
.
4 + x - 5 = 0.
+ x - 5 = 0.
2 - 28x + 66 = 0.
- 28x + 66 = 0.
2 – 6х + 5 = 0.
– 6х + 5 = 0.
(х – 3)(х + 3) = - 5х – 13.
3 = х + 4.
= х + 4.
 = 2.
= 2.
 + 2 = 3х.
+ 2 = 3х.
2 + x - 1 = 4х - 2.
+ x - 1 = 4х - 2.
5 + 3x - 2 = 0.
+ 3x - 2 = 0.
 - 3x = 2х + 24.
- 3x = 2х + 24.
 + 4 = 5.
+ 4 = 5.
 - 64 = 0.
- 64 = 0.
5 = 0.
= 0.
 + 81 = 0.
+ 81 = 0.
 -
-  = 0.
= 0.
 + 8x = 0.
+ 8x = 0.
5х - 20 = 0.
= 0.
 -
- 
 – 1) = 9 – х.
– 1) = 9 – х.
9 - 6x + 2 = 0.
- 6x + 2 = 0.
V. Составьте приведенное квадратное уравнение, зная его корни:
 = 5,
= 5,  = 7.
= 7.
 = - 1,
= - 1,  = 6.
= 6.
 = -
= -  ,
,  =
=  .
.
 = - 0,7,
= - 0,7,  = 0,01.
= 0,01.
VI. При каких значениях  = 0,
= 0,  в уравнении….
в уравнении….
2 + 3x + 2p + 2 = 0.
+ 3x + 2p + 2 = 0.
 + x + p - p = 0.
+ x + p - p = 0.
5 + 2x +
+ 2x +  - 1 = 0
- 1 = 0
 + x – 7p + 14m = 0
+ x – 7p + 14m = 0
VII. При каких значениях  х = 0 – единственный корень уравнения….
х = 0 – единственный корень уравнения….
5 + (p + 1) x +
+ (p + 1) x +  – 1 = 0.
– 1 = 0.
 + p – 2 = 0.
+ p – 2 = 0.
 + 7px +
+ 7px +  = 0.
= 0.
 + (
+ (
VIII. Найдите  и
и  :
:
 + px - 12 = 0,
+ px - 12 = 0, = 4.
= 4.
 + px - 60 = 0,
+ px - 60 = 0, = 15.
= 15.
 + px + 56 = 0,
+ px + 56 = 0, = 7.
= 7.
IX. Найдите  и
и  :
:
 - 8x + q = 0,
- 8x + q = 0, = 12.
= 12.
 + 2x + q = 0,
+ 2x + q = 0, = - 3.
= - 3.
 + x - q = 0,
+ x - q = 0, = 2.
= 2.
X. Найдите  и
и  :
:
 - 26x + c = 0,
- 26x + c = 0, = 0,2.
= 0,2.
 - 10x + c = 0,
- 10x + c = 0, = 1.
= 1.
 + 12x - c = 0,
+ 12x - c = 0, = 5.
= 5.
XI. Решите задачу:
Турист прошел 240 км, закончив путешествие на 6 дней раньше, так как проходил в день на 2 км больше, чем планировал. Сколько дней путешествовал турист и сколько километров в день он проходил?
Двум машинисткам было поручено выполнить некоторую работу. Вторая из них приступила к работе на 1 час позднее первой. Через 3 часа после того, как первая начала работу, им оставалось выполнить еще  всей работы. По окончании работы оказалось, что каждая машинистка выполнила половину всей работы. За сколько часов каждая из них в отдельности могла бы выполнить всю работу?
всей работы. По окончании работы оказалось, что каждая машинистка выполнила половину всей работы. За сколько часов каждая из них в отдельности могла бы выполнить всю работу?
Заключение
Методическое пособие по разделу математики «Квадратные уравнения» можно использовать при подготовке к экзаменам, на дополнительных занятиях и при самостоятельном изучении.
В пособии даются краткие теоретические сведения, решение уравнений. Примеры подобраны с различной степенью трудности: от простых до достаточно сложных и требующих нетрадиционных методов их решения. В принципе это краткий математический справочник, который поможет ученику самостоятельно и глубоко изучить тему «Квадратные уравнения и способы их решения».
Данное пособие может не только помочь пополнить, систематизировать, углубить знания по алгебре, но и способствовать формированию умений применять приемы сравнения, выделения главного, переноса знаний в новую ситуацию; развитию творческих способностей учащихся путем решения заданий более сложного уровня.
Таким образом, изучение различных способов решения квадратных уравнений дает реальную возможность выбора рациональных способов решения квадратных уравнений. Собранными в мини-брошюре материалами могут воспользоваться учащиеся 8-9 классов для изучения и закрепления рациональных способов решения квадратных уравнений.
Список литературы
1. Алгебра. 8 класс. В 2 ч. Ч 1. Учебник для учащихся общеобразовательных учреждений / А.Г. Мордкович. – 13-е изд., стер. – М. : Мнемозина, 2011. – 215 с.: ил.
2. Алгебра. 8 класс. В 2 ч. Ч 2. Задачник для учащихся общеобразовательных учреждений / [А.Г. Мордкович и др.]: под редакцией А.Г. Мордковича – 13-е изд., стер. – М. : Мнемозина, 2011. – 271 с.: ил.
3. Выгодский М.Я. Справочник по элементарной математике. – М. государственное издательство физико-математической литературы, 1970.
4. Галицкий М.Л., Гольдман М., Звавич Л.И. Сборник задач по алгебре для 8-9 классов: учебное пособие для учащихся школ и классов с углубленным изучением математики:4-е изд.-М.: Просвещение, 1997.
5. Макарычев Ю.Н., Миндюк Н.Г. Алгебра. Учебник для 8 класса. М., Просвещение, 2011.
6. Макарычев Ю.Н., Миндюк Н.Г. Дополнительные главы к школьному учебнику. 8 класс М.,
7. Никольский С.М., Потапов М.К. Алгебра. Пособие для самообразования. – М.: Наука. Главная редакция физико-математической литературы, 1984 – 288 с.






 , а правая – нуль.
, а правая – нуль.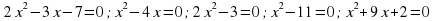
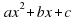 = 0, (1)
= 0, (1)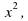 число b - коэффициентом при
число b - коэффициентом при 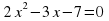
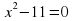
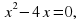
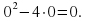
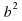 − 4ac.
− 4ac.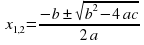 .
.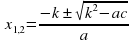 , где
, где 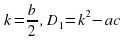 .
.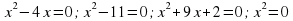
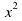 + px + q = 0 , (2)
+ px + q = 0 , (2)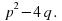 (3)
(3)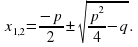
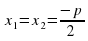 .
.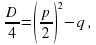 имеющее тот же знак, что и D.
имеющее тот же знак, что и D.
















