ГБОУ СПО ЛНР «Стахановский поплитехнический колледж»
МИНИ-КОНСПЕКТ
по
ГЕОМЕТРИИ
на тему:
«МНОГОГРАННИКИ. ТЕЛА ВРАЩЕНИЯ»
Разработала
преподаватель математики
М.А.Кидалова
г. Стаханов
2022 г.
История развития геометрии пирамиды
Начало геометрии пирамиды было положено в Древнем Египте и Вавилоне, однако активное развитие получило в Древней Греции. Первый, кто установил, чему равен объем пирамиды, был Демокрит [2], а доказал Евдокс Книдский. Древнегреческий математик Евклид систематизировал знания о пирамиде в XII томе своих «Начал», а также вывел первое определение пирамиды: телесная фигура, ограниченная плоскостями, которые от одной плоскости сходятся в одной точке.
Египетские пирамиды — величайшие архитектурные памятники Древнего Египта, среди которых одно из «семи чудес света» — пирамида Хеопса и почётный кандидат «новых семи чудес света» — Пирамиды Гизы. Пирамиды представляют собой огромные каменные сооружения пирамидальной формы, использовавшиеся в качестве гробниц для фараонов Древнего Египта. Всего в Египте было обнаружено 118 пирамид. При упоминании египетских пирамид, как правило, имеют в виду Великие Пирамиды, расположенные в Гизе, неподалёку от Каира. Но они не являются единственными пирамидами в Египте. Многие другие пирамиды гораздо хуже сохранились и сейчас напоминают холмы или груды камней. Египетские пирамиды являются одним из чудес света, и не мудрено, ведь мысль о том, что люди вооруженные лишь простыми механическими устройствами, построили подобные громады, которые продолжают восхищать нас, хотя со времени их создания прошли тысячелетия. Первая пирамида была построена в 2670 г.до.н.э. Пирамида Джосера расположена в Саккаре, к северо-востоку от древнего Мемфиса, в 15 км от Гизы. Её высота составляет 62 м. Великими пирамидами называют расположенные в Гизе пирамиды фараонов Хеопса,Хефрена и Микерина. В отличие от пирамиды Джосера,эти пирамиды имеют не ступенчатую ,а строго геометрическую,пирамидальную форму. Эти пирамиды относятся к периоду IV династии. Стены пирамид поднимаются под углом от 51°(пирамида Менкаура) до 53°(пирамида Хефрена) к горизонту. Грани точно ориентированы по сторонам света. Пирамида Хеопса построена на массивном природном скальном возвышении, которое оказалось в самой середине основания пирамиды. Его высота около 9 м. Самой большой является пирамида Хеопса. Первоначально её высота составляла 146,6 м,однако из-за того,что сейчас отсутствует облицовка пирамиды ,её высота к настоящему времени уменьшилась до 138,8 м. Длина стороны пирамиды — 230м. В пирамидах были найдены гробницы фараонов. Интересно ещё и то,что Египетские пирамиды помогают прийти человеку в состояние необычного сознания, скажем ,транса .
Развертка прямой треугольной призмы
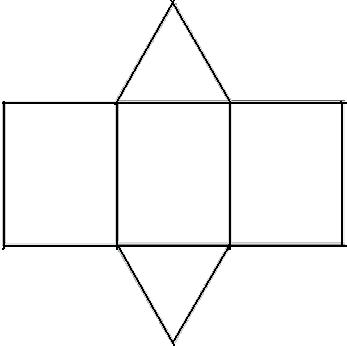
НАКЛАННАЯ ПРИЗМА
Н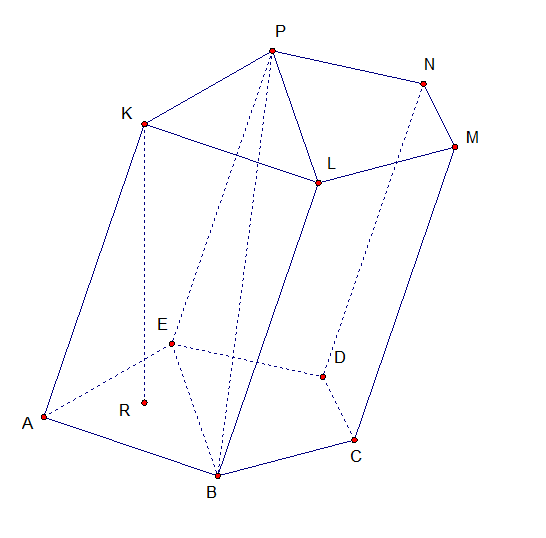 азовите основание.
азовите основание.
Назовите боковые ребра.
Назовите боковые грани.
Назовите вершины.
Назовите высоту.
Назовите сечение.
ПРЯМАЯ ПРИЗМА НАКЛОННАЯ ПРИЗМА
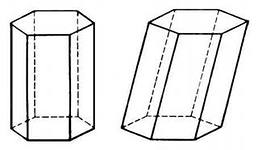
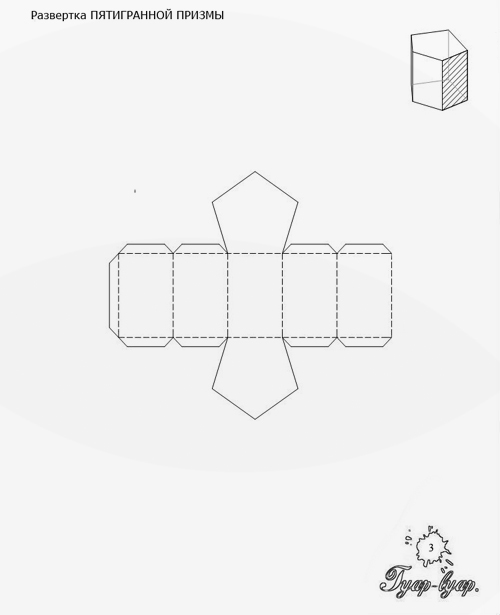
К УБ – это прямая правильная
УБ – это прямая правильная
4-х угольная призма.
ГРАНИ – квадраты.
Объем куба
Объем куба равен кубу длины его грани.
Формула объема куба
V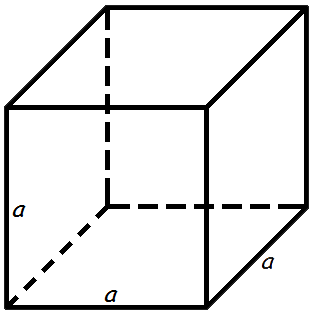 =
= 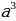
где
V- объем куба,
а - длина грани куба.
Объем призмы
Объем призмы равен произведению площади основания призмы, на высоту.
Формула объема призмы
 V = So h
V = So h
где
V - объем призмы,
So - площадь основания призмы,
h - высота призмы.
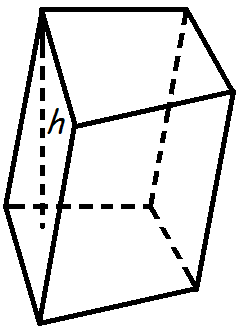
Объем параллелепипеда
Объем параллелепипеда равен произведению площади основания на высоту.
Формула объема параллелепипеда
V = So · h
= So · h
где
V- объем параллелепипеда,
So - площадь основания,
h - длина высоты.
Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
Формула объема прямоугольного параллелепипеда
V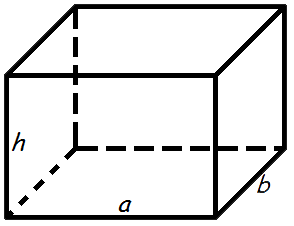 =a·b·h
=a·b·h
где
V- объем прямоугольного параллелепипеда,
a - длина,
b - ширина,
h - высота.
Объем пирамиды
Объем пирамиды равен трети от произведения площади ее о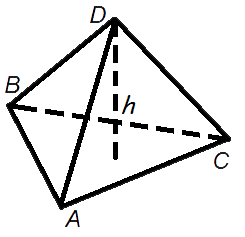 снования на высоту.
снования на высоту.
Формула объема пирамиды
где
V - объем пирамиды,
So- площадь основания пирамиды,
h- длина высоты пирамиды.
Объем правильного тетраэдра
Ф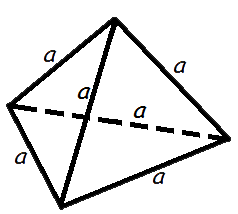 ормула объема правильного тетраэдра
ормула объема правильного тетраэдра
где
V - объем правильного тетраэдра,
a - длина ребра правильного тетраэдра.
Объем цилиндра
Объем цилиндра равен произведению площади его основания на высоту.
Формулы объема цилиндра
V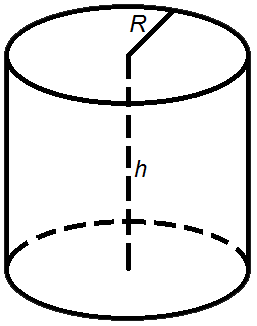 = π R2h
= π R2h
где
V - объем цилиндра,
So - площадь основания цилиндра,
R - радиус цилиндра,
h - высота цилиндра,
π = 3.141592
Объем конуса
Объем конуса равен трети от произведению площади его основания на высоту.
Ф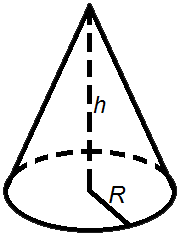 ормулы объема конуса
ормулы объема конуса
где
V - объем конуса,
So - площадь основания конуса,
R- радиус основания конуса,
h - высота конуса.
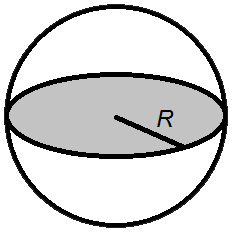
Объем шара
Объем шара равен четырем третим от его радиуса в кубе помноженого на число пи.
Формула объема шара
где
V- объем шара,
R - радиус шара,
π = 3.141592
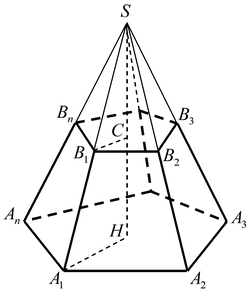
П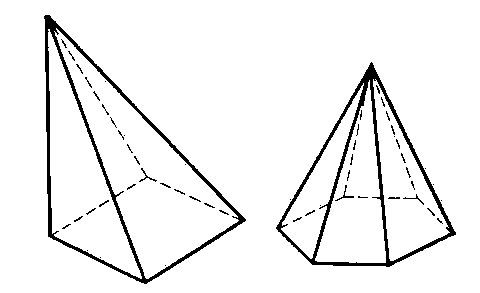 РЯМАЯ И НАКЛОННАЯ ПИРАМИДА
РЯМАЯ И НАКЛОННАЯ ПИРАМИДА
Пирамида называется прямой, если ее высота проектируется в центр основании
Элементы пирамиды:
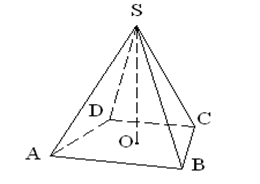
SO – высота;
ABCD – основание;
ASB - боковая грань;
SA ; SB …. – боковое ребро.
ПРАВИЛЬНАЯ ПИРАМИДА, АПОФЕМА
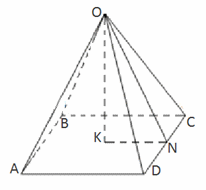
Пирамида называется правильной, если в ее основании лежит
правильный многоугольник и высота проектируется
в центр основания.
Апофемой в правильной пирамиде называется высота боковой
грани (ОN).
Апофема является высотой треугольника ДОС,
следовательно, отрезок ДС делится точкой N
пополам. Обозначается апофема обычно L.
УСЕЧЕННАЯ ПИРАМИДА
Если пирамиду пересечь плоскостью параллельной
основанию, то получится усеченная пирамида, которая
имеет два параллельных основания.
Основания усеченной пирамиды – подобные
многоугольники.
Боковая грань усеченной пирамиды – трапеция.
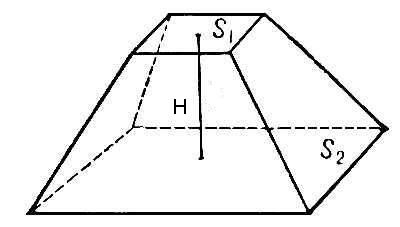
УСЕЧЕННАЯ ПИРАМИДА
Усеченной пирамидой называется часть пирамиды (полной пирамиды), заключенная между плоскостью основания и параллельной ей секущей плоскостью.
Параллельные грани усеченной пирамиды называются основаниями; отрезок прямой, перпендикулярной основаниям и заключенный между ними, называется высотой усеченной пирамиды, длина этого отрезка также называется высотой усеченной пирамиды.
Усеченная пирамида называется правильной, если она получена указанным выше способом из правильной полной пирамиды. Основания усеченной пирамиды --- правильные многоугольники, а центр одного основания проектируется в центр другого. Термины "боковые ребра", "боковые грани", "апофема" и свойства симметрии для пирамид и усеченных пирамид аналогичны.
Усеченная пирамида получается, если от полной пирамиды "отсечь" подобную ей пирамиду плоскостью, параллельной основанию. Значит, и боковую поверхность, и объем усеченной пирамиды можно вычислить, зная коэффициент подобия, а также боковую поверхность и объем полной пирамиды.
Математически верное определение
... Плоскость, параллельная основанию пирамиды и пересекающая ее боковые ребра, отсекает от нее подобную пирамиду. Другая часть представляет собой многогранник, который называется усеченной пирамидой. Грани усеченной пирамиды, лежащие в парллельных плоскостях, называются основаниями; остальные грани называются боковыми гранями.
Усеченная пирамида, которая получается из правильной пирамиды, также называется правильной. Боковые грани правильной усеченной пирамиды --- равные равнобокие трапеции; их высоты называются апофемами.
Площадь поверхности пирамиды
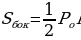
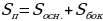
Площадь поверхности призмы
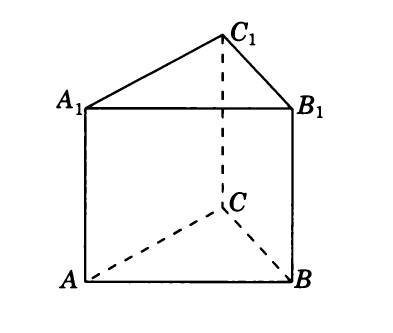
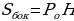
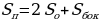 икосаэдр
икосаэдр
Грани – правильные треугольники
В одной вершине сходится 5 ребер
одной вершине сходится 5 ребер
Число ребер – 30
Число вершин – 12
Число граней - 20
додекаэдр
Грани – правильные пчтиугольники
В одной вершине сходится 3 ребра
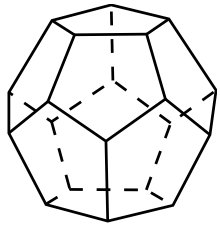 Число ребер – 30
Число ребер – 30
Число вершин – 20
Число граней - 12
ОКТАЭДР
Грани – правильные треугольники
В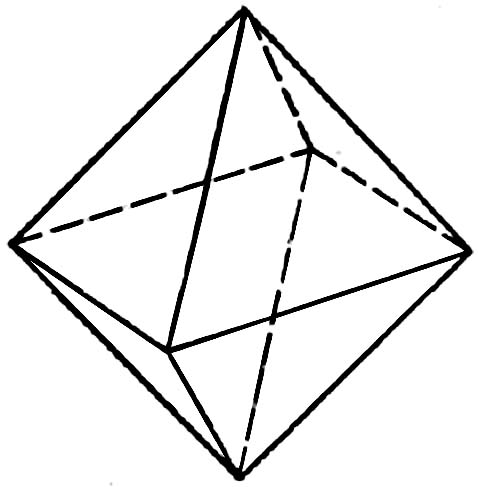 одной вершине сходится 4 ребра
одной вершине сходится 4 ребра
Число ребер – 12
Число вершин – 6
Число граней - 8
куб
Грани – квадраты
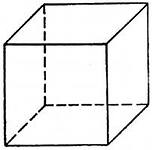 В одной вершине сходится 3 ребра
В одной вершине сходится 3 ребра
Число ребер – 12
Число вершин – 8
Число граней - 6
тетраэдр
Грани – правильные треугольники
В одной вершине сходится 3 ребра
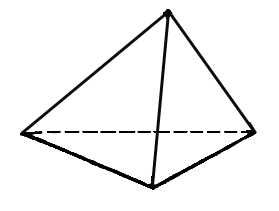 Число ребер – 6
Число ребер – 6
Число вершин – 4
Число граней - 4







 азовите основание.
азовите основание.

 УБ – это прямая правильная
УБ – это прямая правильная  =
= 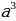
 V = So h
V = So h = So · h
= So · h =a·b·h
=a·b·h снования на высоту.
снования на высоту. ормула объема правильного тетраэдра
ормула объема правильного тетраэдра = π R2h
= π R2h ормулы объема конуса
ормулы объема конуса
 РЯМАЯ И НАКЛОННАЯ ПИРАМИДА
РЯМАЯ И НАКЛОННАЯ ПИРАМИДА



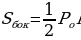
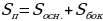

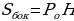
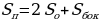 икосаэдр
икосаэдр одной вершине сходится 5 ребер
одной вершине сходится 5 ребер Число ребер – 30
Число ребер – 30 одной вершине сходится 4 ребра
одной вершине сходится 4 ребра В одной вершине сходится 3 ребра
В одной вершине сходится 3 ребра Число ребер – 6
Число ребер – 6









