Построение комбинационных схем, реализующих МДНФ и МКНФ заданной логической функции от 4-х переменных в базисах И-НЕ, ИЛИ-НЕ
Минимизация ЛФ по таблице истинности
1)устр-во, имеющее 3 входа (a, b, c) и 1 выход (out). На выходе дб логическая 1 толькокогда 1 поступ на кол входов В ост сл на выходе д б 0.
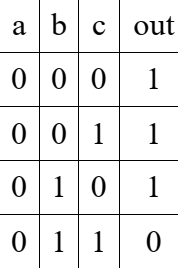
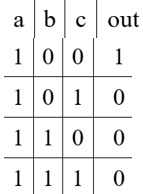
СДНФ 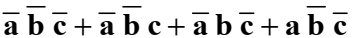
СКНФ 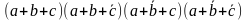
после минимизации
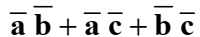
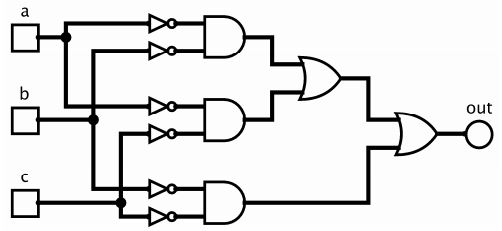
Реализация минимальной ДНФ
метод диаграмм Вейча или карт Карно
Пусть табл истинности задана в 16-ичной форме 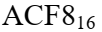 или
или
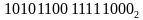
Разместим единич значения функции на диагр Вейча, функции 4 переменных
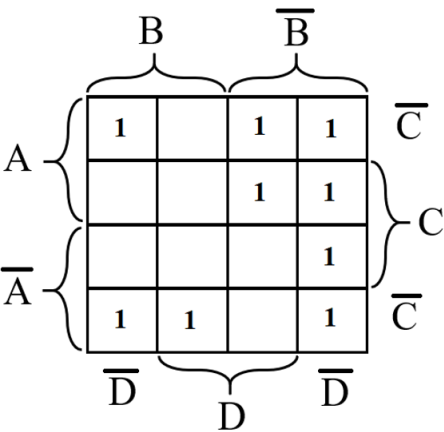
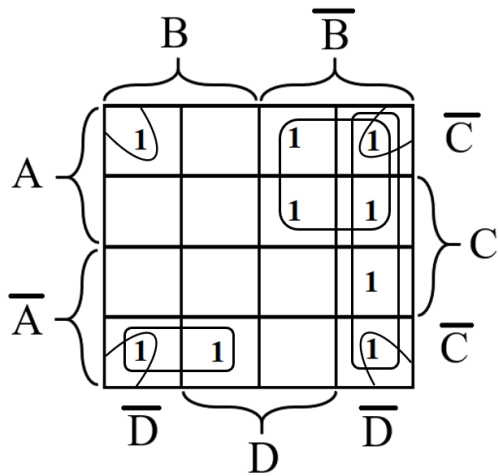 рис18
рис18
выделим интервалы, где F=1. Размер интервалов = степени двойки.При выделении н помнить, что диаграмма Вейча осущ развертку пространств фигуры, поэтому некот интервалы мо разрываться краями диаграммы (см рис 18)
1) для каждого интервала запишем мин конъюнкцию, куда б вх только те перем и их отрицания, кот сохраняют свое знач на этом интервале
2) объедин при пом дизъюнкции имеющ мн-во минимальных конъюнкций
Для вертикальн инт-ла рис 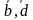 сохр свое зн на протяжении всего интервала, а перем
сохр свое зн на протяжении всего интервала, а перем  меняется ЛФ этого интервала не зависит от с и равна
меняется ЛФ этого интервала не зависит от с и равна 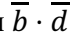
Для данного рис ЛФ 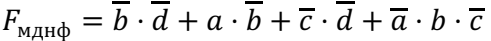
Диаграмма Вейча (Карно) для функции 4 переменных имеет ыид матрицы 4x4
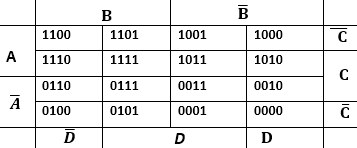 табл1
табл1
запишем в клетки значения 1 если F=1 га этом наборе переменных
или оставим пустую клетку если на них F=9 Получим табл 2
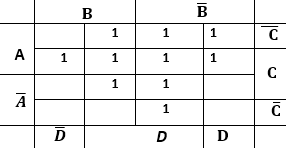 табл2
табл2
Выделим на ней цепочки длиной 2 или 4 в одном строке или столбце
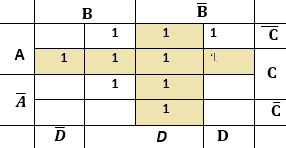
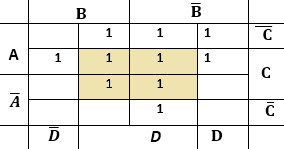
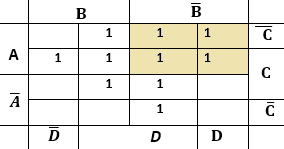
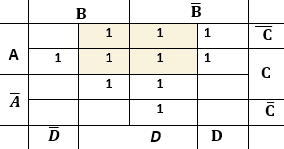
получилось 5 цепочек-кластеров. Записываем произведение пары тех переменных которые постоянны на гранях каждого кластера. Получим
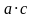 ,
, 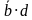 для рис1
для рис1 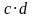 для рис 2 ,
для рис 2 , 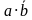 для рис 3 ,
для рис 3 , 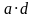 для рис 4
для рис 4
соединяем все члены конъюнкциями получим
1б) Проверка по программе
вводим в окно программы W80L в качестве входных данных форму СДНФ полученную в работе 1 В результате получим выражение
полностью совпавшее с (1)
Можно так же записать в виде
3)Реализация схемы МДНФ в базисе И-НЕ
В (1) сделаем замену членов освобо от дизъюнкций по закону Моргана


подст их в (1) получим выр функции только через конбюнк и отрицания

Реализация схемы МДНФ в базисе ИЛИ-НЕ
В (1а) сделаем замену членов освоб от конъюнк по зну Моргана
получим
МДНФ в базисе И-НЕ МДНФ в базисе ИЛИ-НЕ
5ИЛИ, и 4 НЕ 5И, и 5 НЕ
5)Реализация схемы МКНФ в базисе И-НЕ
МКНФ строится по нулевым знач логической функции.
табл 0 выделения интервалов для МКНФ
Для каждого интервала запишем мин дизъюнкцию, куда б вх только те перем и их отриц, кот сохр св знач на этом интервале. получим
Реализация МКНФ в базисе И-НЕ
преобразуем по законам Моргана выражение МКНФ выше
МКНФ в базисе И-НЕ МКНФ в базисе ИЛИ-НЕ
вар 17 табл истинности 
Выделим на ней цепочки длиной 2 или 4 в одном строке или столбце




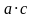 ,
, 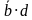 для рис1
для рис1 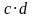 для рис 2 ,
для рис 2 , 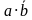 для рис 3 ,
для рис 3 , 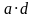 для рис 4
для рис 4
соединяем все члены конъюнкциями получим
 (1)
(1)
в базисе И-НЕ заменим
получим
в базисе ИЛИ-НЕ
получим
Сдема реализации (1.2) в Multisim приведена ниже
МДНФ в базисе И-НЕ МДНФ в базисе ИЛИ-НЕ
Построение МКНФ по диаграмме Вейча (Карно)
Возьмем за основу диаграмму для МДНФ. восстановим нули на пустых клетках, а единицы теперь изображать не будем.Поменяем местами обозначения переменных на отрицания
Выделим на ней цепочки длиной 2 или 4 в одном строке или столбце
(переменные не изменяющиеся в цепочке соединены знаком +)
перемножая суммы во всех цепочках получим МКНФ
запись в базисе И-НЕ
сделаем замену членов в (2) освободившись от дизъюнкций по закону Моргана



получим
Cхема реализации ниже требует 4И, и 6 НЕ (всего 10 элементов)
6)Реализация схемы МКНФ в базисе ИЛИ-НЕ
сделаем замену членов освободившись от конъюнкций по закону Моргана
Cхема реализации ниже требует 5ИЛИ, и 4 НЕ (всего 9 элементов)
Следует отметить, что метод диаграмм Вейча (карт Карно) можно применять и для функций более чем 4 переменных. Там есть свои особенности, что изложено в [1]
В некоторых случаях интересны вопросы минимизации не полностью определённых булевых функций
Литература
1)Лобанов В.И. Решебник по русской логике
2) Смирнов С.С. Информатика: Методические указания по выполнению практических и лабораторных работ М., МИРЭА, 2018.









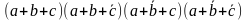

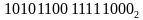

 рис18
рис18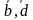 сохр свое зн на протяжении всего интервала, а перем
сохр свое зн на протяжении всего интервала, а перем  меняется ЛФ этого интервала не зависит от с и равна
меняется ЛФ этого интервала не зависит от с и равна  табл1
табл1 табл2
табл2



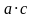 ,
, 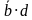 для рис1
для рис1 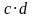 для рис 2 ,
для рис 2 , 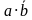 для рис 3 ,
для рис 3 , 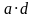 для рис 4
для рис 4 



















