МУНИЦИПАЛЬНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №5 Г УНЕЧА БРЯНСКОЙ ОБЛАСТИ
ПРОЕКТ
Тема : Многогранники – геометрические тела
Выполнила :
Проворная Кристина, ученица 10а класса
Руководитель :
Смолко Лариса Георгиевна учитель математики
г.Унеча- 2021г
В начале XX века великий французский архитектор Ле Корбюзье сказал:
«Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Все вокруг – геометрия».

Оглавление
Введение ------------------------------------------------------------------------------------------3
Глава 1. Что такое геометрия
1.1.История возникновения геометрии? --------------------------------------------4
1.2.Основные геометрические фигуры. --------------------------------------------7
Глава 2. Геометрия вокруг нас
2.1.Геометрия у нас дома.---------------------------------------------------------------9
2.2. Геометрия на улице.----------------------------------------------------------------9
2.3 Геометрия в космосе----------------------------------------------------------------
2.4 Геометрия в природе.----------------------------------------------------------------
2.5 Геометрия у животных.--------------------------------------------------------------
2.6 Геометрия в транспорте.------------------------------------------------------------
2.7 Геометрия в архитектуре-----------------------------------------------------------
Глава 3. Геометрические тела и их развертки.---------------------------------------------
3.1 Куб.
3.2 Параллелепипед.
3.3 Октаэдр.
Заключение--------------------------------------------------------------------------------------11
Литература---------------------------------------------------------------------------------------12
Приложения -------------------------------------------------------------------------------------13
Введение
Для защиты проекта я выбрала тему: “ Многогранники – геометрические тела“, потому что с трудом понимаю предмет геометрию, для меня она очень сложная : не знаю термины, пространственное восприятие геометрических тел , а в следующем году хочу хорошо сдать экзамен по математике .
Чтобы лучше понять геометрию, очень важно при решении задач осознавать внешние формы многогранника.
Например, при решении задачи, при заданных параметрах найти объем геометрических тел, трудно представить мысленно фигуру .
И поэтому цель моего проекта : создание геометрических тел для понимания , представления и решения задач.
Задачи :
Изучить информацию по данной теме
Начертить чертежи геометрических тел
Оформить геометрические тела, как методическое пособие
Актуальность.
Было бы неверно утверждать, что до работы над проектом я совсем не занимался геометрией и ничего о ней не знаю. Каждый из нас без труда сможет привести примеры различных геометрических тел, встречающихся в окружающем нас мире: жилой дом, камень, дерево, капля воды и многое другое. А с многими геометрическими понятиями мы уже знакомы: круг, квадрат, угол, куб, измерение отрезков, площадь, объем и так далее. И если взглянуть на окружающие нас предметы как на геометрические тела, то можно сказать, например, что дом и кирпич имеют одинаковую форму – форму параллелепипеда и отличаются лишь размерами. При изучении геометрических тел не берется во внимание, из какого материала они сделаны, какого цвета, в каком состоянии находятся. Этим занимается физика, химия, биология. Изучая геометрию нас будет интересовать только форма и размеры предметов, их взаимное расположение. Любой современный человек в своей жизни не может обойтись без знания математики, а в частности без умений увидеть в окружающем нас мире геометрические тела и объекты.
Проектное предложение
Методы исследования:
- изучение литературы по данному вопросу
- наблюдение в повседневной жизни
Теоретическая значимость проекта заключается в том, что мною были систематизированы теоретические знания по теме проекта из различных информационных источников.
Практическая значимость данного проекта определена тем, что я научилась делать развертки и модели различных геометрических тел, которые сегодня представляю вашему вниманию.
1.Что такое геометрия?
Геоме́трия (от др.-греч. γεωμετρία, от γῆ — земля и μετρέω — измеряю) — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения[1].

1.1 История возникновения геометрии.
Ещё в эпоху неолита люди составляли на стенах пещер орнаменты из треугольников, ромбов, прямоугольников, кругов. Древние художники тонко чувствовали красоту геометрических форм; наскальные рисунки, выполненные с большой любовью к природе, радовали глаз. Человек отмечал равенство, симметрию, подобие фигур. Со временем он научился использовать свойства фигур в практической жизни. Геометрия - древнейшая наука, а первые геометры производили расчеты свыше тысячи лет назад.
Земледельцы, жившие на берегах великих рек: Нила, Тигра и Ефрата, Инда и Ганга, искусно делили свои земельные участки. Для проведения замеров были выработаны первые правила новой науки - "геометрии", что в переводе с греческого и означает - "землемерие".
Геометрические фигуры интересовали наших предков не только потому, что помогали решать практические задачи, такие как строительство жилища, которое имело формы различных геометрических тел. Некоторые из фигур имели для людей магическое значение. Так, треугольник считался символом жизни, смерти и возрождения; квадрат - символом стабильности. Круг - знаком совершенства.
Великий немецкий математик Вильгельм Лейбниц сказал: «Кто хочет ограничиться настоящим, без знания прошлого, тот никогда его не поймет».
Откуда пошла геометрия. Геометрия… Откуда взялось это слово? Что оно означает? Попробуем разгадать его смысл. «Гео» означает «Земля», «метр» - это единица измерения длины (от греческого слова «метрео» - «измеряю». Таким образом, получается, что геометрия в переводе с греческого означает «измерение земли» или «землемерие».
Какова же история ее возникновения? Такой вопрос задавали еще в Древней Греции и отвечали на него так: «Геометрия была открыта египтянами и возникла при измерении земли. Нет ничего удивительного в том, что эта наука как и другие, возникла из потребностей человека. Всякое возникающее знание из несовершенного состояния переходит в совершенное. Зарождаясь путем чувственного восприятия, оно постепенно становится предметом рассмотрения и наконец, делается достоянием разума». Эти замечательные слова приписывают греческому ученому Евдему Родосскому, жившему в IVв. до н.э. В «Энциклопедическом словаре юного математика» написано: «Геометрия – одна из наиболее древних математических наук. Первые геометрические факты мы находим в вавилонских клинописных таблицах и египетских папирусах (III тысячелетие до н.э.), а также в других источниках».
Для первобытных людей важную роль играла форма окружавших их предметов. По форме и цвету они отличали съедобные грибы от несъедобных, пригодные для построек породы деревьев от тех, которые годятся лишь на дрова, вкусные орехи от горьких. Особенно вкусными казались им орехи кокосовой пальмы, похожие на шар. А добывая каменную соль, люди наталкивались на кристаллы, имевшие форму куба. Специальных названий для геометрических фигур, конечно, не было. Говорили: «такой же, как кокосовый орех» или «такой же, как соль». Так, овладевая окружающим их миром, люди, знакомились с простейшими геометрическими формами.
Уже 200 тысяч лет тому назад были изготовлены орудия сравнительно правильной геометрической формы, а потом люди научились шлифовать их.
А когда люди стали строить дома из дерева, пришлось глубже разбираться в том, какую форму следует придавать стенам и крыше, какой формы должны быть брёвна и т.д. Сами того не зная, люди все время занимались геометрией: женщины, изготавливая одежду, охотники, изготавливая наконечники для копий или бумеранги сложной формы, рыболовы, делая такие крючки из кости, чтобы рыба с них не срывалась.
Когда стали строить здания из камня, пришлось перетаскивать тяжелые каменные глыбы. Для этого применялись катки. И заметили, что перекатка проще, если взять кусок дерева с почти одинаковой толщиной в начале и в конце. Так люди познакомились с одним из важнейших тел – цилиндром. Скалками цилиндрической формы пользовались и женщины, раскатывая белье после стирки.
Перевозить грузы на катках было довольно тяжело потому, что сами древесные стволы весили много. Чтобы облегчить работу, стали вырезать из стволов тонкие круглые пластинки и с их помощью перетаскивать грузы. Так появилось первое колесо.
Но не только в процессе работы знакомились люди с геометрическими фигурами. Издавна они любили украшать себя, свою одежду, свое жилище (бусинки, браслеты, кольца, украшения из драгоценных камней и металлов, роспись дворцов).
Для того чтобы взимать налоги с земли, необходимо было знать их площадь. Гончару необходимо было знать, какую форму следует придать сосуду, чтобы в него входило то или иное количество жидкости. Астрономы, наблюдавшие за небом и дававшие на основе этих наблюдений указания, когда начинать полевые работы, должны были научиться определять положение звезд на небе. Для этого понадобилось измерять углы.
Так практическая деятельность людей привела к дальнейшему углублению знаний о формах фигур, развитию геометрии. Люди стали учиться измерять и площади, и объемы, и длины и т.д. Древние египтяне были замечательными инженерами. До сих пор не могут до конца разгадать загадки огромных гробниц Египетских царей – Фараонов.
Египетские пирамиды насчитывают 4800 лет, а их строительство, очевидно, требовало достаточно точных геометрических расчетов, так как состоят они из каменных блоков весом 15 тонн, и эти «кирпичики» так подогнаны друг к другу, что не возможно между ними протиснуть и почтовую открытку. А при строительстве использовали лишь простейшие механизмы – рычаги и катки.
«Все боится времени, но само время боится пирамид».
В Вавилоне при раскопках ученые обнаружили остатки каменных стен, высотой в несколько десятков метров, а высота Вавилонской башни достигает 82 метра. Без математических знаний все эти сооружения невозможно было бы построить.
Но особо важной была задача распределения земельных участков. В Египте плодородная земля тянется узкой полоской в долине Нила, а за ее пределами простирается пустыня. Поэтому каждый ее клочок представлял большую ценность. Ежегодно разливы Нила смывали границы участков, нужно было восстанавливать их как можно точнее. Этим занимались специальные землемеры, которые и были, можно сказать, первыми геометрами.
И все же математические знания египтян и вавилонян были разрозненные и представляли собой свод правил, проверенных практикой, поэтому правила надо было зазубривать, не понимая, почему надо применять то, а не другое.
Если в Древнем Египте геометрия была сугубо прикладной наукой, то в древней Греции она стала математической теорией. И имена знаменитых греков будут постоянно встречаться нам в курсе геометрии.
Почти все великие ученые древности и средних веков были выдающимися геометрами. Девиз Академии Платона гласил: "Да не войдёт сюда не знающий геометрии"
Настает время привести все разрозненные знания в систему.
Евклид жил в Александрии около 300 года до нашей эры, был современником царя Птолемея I и учеником Платона. Славу Евклиду создал его собирательный труд «Начала». Произведение состояло из 13 томов, описанная в этих книгах геометрия получила название Евклидова. Величайшая заслуга его состояла в том, что он подвел итог построению геометрии, придал ее изложению столь совершенную форму, что на 2 тысячи лет «Начала» стали основным руководством по геометрии.
Конечно, геометрия не может быть создана одним ученым. В работе Евклид опирался на труды десятков предшественников и дополнил работу своими открытиями и изысканиями. Сотни раз книги были переписаны от руки, а когда изобрели книгопечатание, то она много раз переиздавалась на языках всех народов и стала одной из самых распространенных книг в мире.
В одной легенде говорится, что однажды египетский царь Птолемей I спросил древнегреческого математика, нет ли более короткого пути для понимания геометрии, чем тот, который описан в его знаменитом труде, содержащемся в 13 книгах. Ученый гордо ответил: " В геометрии нет царской дороги".
В течение многих веков «Начала» были единственной учебной книгой, по которым молодежь изучала геометрию. Были и другие. Но лучшими признавались «Начала» Евклида. И даже сейчас, в наше время, учебники написаны под большим влиянием «Начал» Евклида.
Несмотря на то, что содержание геометрии расширилось далеко за пределы учения о земле, она по-прежнему продолжает называться «Геометрией».
1.2 Основные геометрические фигуры
Геометрические фигуры, точки которых лежат в одной плоскости, изучает планиметрия.
ТОЧКА- одно из основных понятий геометрии. При систематическом изложении геометрии точка обычно принимается за одно из исходных понятий.
ПРЯМАЯ- одно из основных понятий геометрии. Можно провести через любые две точки и притом одну.
ОКРУЖНОСТЬ- замкнутая плоская кривая, все точки которой одинаково удалены от ее центра O.
ПРЯМОУГОЛЬНИК- четырёхугольник, у которого все углы прямые.
КВАДРАТ- равносторонний прямоугольник.
КРУГ- часть плоскости ограниченная окружностью.
ТРАПЕЦИЯ- четырехугольник, у которого две стороны параллельны, а две другие нет.
ПАРАЛЛЕЛОГРАММ- четырехугольник у которого противоположные стороны попарно параллельны.
РОМБ- параллелограмм у которого все стороны равны.
Геометрические фигуры, точки которых лежат в разных плоскостях, изучает стереометрия.
ПАРАЛЛЕЛЕПИПЕД- призма, основанием которой служит параллелограмм. «Призма» - латинская форма греческого слова «присма» - опиленная (имелось в виду опиленное бревно)
КОНУС- геометрическое тело, образованное вращением прямоугольного треугольника вокруг одного из его катетов. «Конус» - латинская форма греческого слова «Конос», означающего сосновую шишку.
ЦИЛИНДР- геометрическое тело, образованное вращением прямоугольника вокруг одной из его сторон. Означает «валик», «каток».
ПИРАМИДА- многогранник, основание которого представляет собой многоугольник, а остальные грани — треугольники с общей вершиной. Это название пошло от египетских пирамид.
ШАР- часть пространства ограниченного сферой.
Глава 2. Геометрия вокруг нас
2.1. Геометрия у нас дома.
Все предметы в нашем доме напоминают различные геометрические фигуры. Рассмотрим и опишем некоторые из них. /Приложение 1.0/
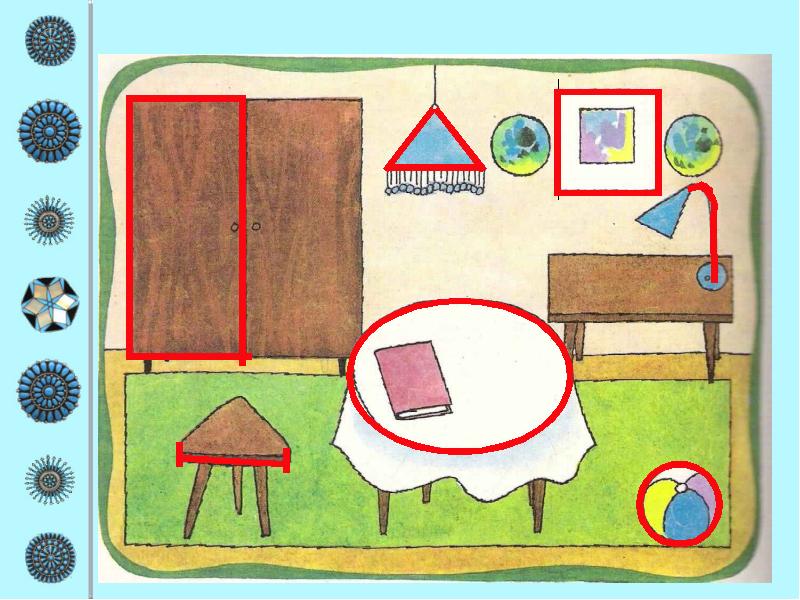
Заглянем на кухню. Холодильник, микроволновая печь, газовая плита, кухонный шкаф, стиральная машина имеют форму прямоугольного параллелепипеда. Потому что, как и у параллелепипеда, все противолежащие грани прямоугольники их всего 6, 12 ребер, 8 вершин, есть три измерения – длина, ширина, высота. Еще можно эти предметы назвать прямыми призмами, у них все углы между гранями прямые. /Приложение 1.1/
А чайник похож на усеченный конус. Дно чайника круг, а крышку откроем, увидим еще одну окружность только меньшего размера. /Приложение 1.2/
Лейка похожа на конус. /Приложение 1.3/
Кастрюли цилиндрической формы. И действительно – у них имеется два круга, лежащие в параллельных плоскостях и стенка, которую можно представить как множество отрезков, соединяющих соответствующие точки на этих кругах. /Приложение 1.4/
Тарелки напоминают круг, край тарелки - окружность. /Приложение 6/
Крышка стола прямоугольник, я попробовала измерить углы они прямые.
Давайте заглянем вовнутрь холодильника и что же мы видим, и здесь без геометрии не обошлось. На полках стоят «цилиндры» - банка сгущенки, банка молока, консервы, кусок колбасы, а сыр напоминает круг. /Приложение 7/
Прогуляемся по спальне. Шкаф, кровать, трельяж, стол – прямоугольные параллелепипеды. Ковер на полу прямоугольной формы. Горшки с цветами на подоконниках цилиндрической формы. Абажур формой конуса.
Толстая книга похожа на параллелепипед. Двери имеют форму прямоугольников. Стены, потолок, окна так же напоминают прямоугольники.
2.2 Геометрия на улице
В настоящее время г. Унеча насчитывается более 70 перекрестков из них:
- один из главных перекрестков улиц Луначарского и Октябрьская.
- Перекресток улиц Ленина и Транспортной.
2.3 Геометрия в космосе
Орбиты планет - окружности, центром которых является Солнце. Спиральная галактика. Один из самых геометрически ясных феноменов Солнечной системы — странный «островок стабильности» на штормовом Северном полюсе Сатурна, имеющий четкую форму шестиугольника. Геометрия может помочь больше узнать о космосе и космических телах. Например, древнегреческий ученый Эратосфен с помощью геометрии измерил длину окружности земного шара. Он обнаружил, что когда Солнце стоит в Сиене (Африка) над головой, в Александрии, расположенной в 800км, оно отклоняется от вертикали на 7°. Эратосфен заключил, что из центра Земли Солнце видно под углом 7° и, следовательно, окружность земного шара равна 360:7•800=41140км. Есть много и других интересных опытов благодаря которым мы все больше и больше узнаем о космосе с помощью геометрии. Представьте себе космический корабль, который приближается к какой-то планете. Системы астронавигации корабля состоят из телескопов с фотоэлементами, радиолокаторов, вычислительных устройств. Пользуясь ими, космонавты определяют углы, под которыми видны различные небесные тела, и вычисляют расстояния до них. Штурман экипажа установил расстояние до планеты. Однако ещё неизвестно, над какой точкой поверхности планеты корабль находится. Ведь этим расстоянием, как радиусом, можно очертить в пространстве целую сферу, шар, и корабль может быть в любом месте его поверхности. Это и есть первая поверхность положения, которую можно сравнить – хотя и условно – с улицей из нашего “земного” примера. Но если штурман определит расстояние до другой планеты и вычертит второй шар, пересекающийся с первым, положение корабля уточнится. Вспомните: пересечение двух сфер даёт окружность. Где-то на этой окружности и должен находиться корабль. (Вот он, “переулок”!) Третье измерение – относительно ещё одной планеты – отметит на окружности уже две точки, одна из которых и есть место корабля.
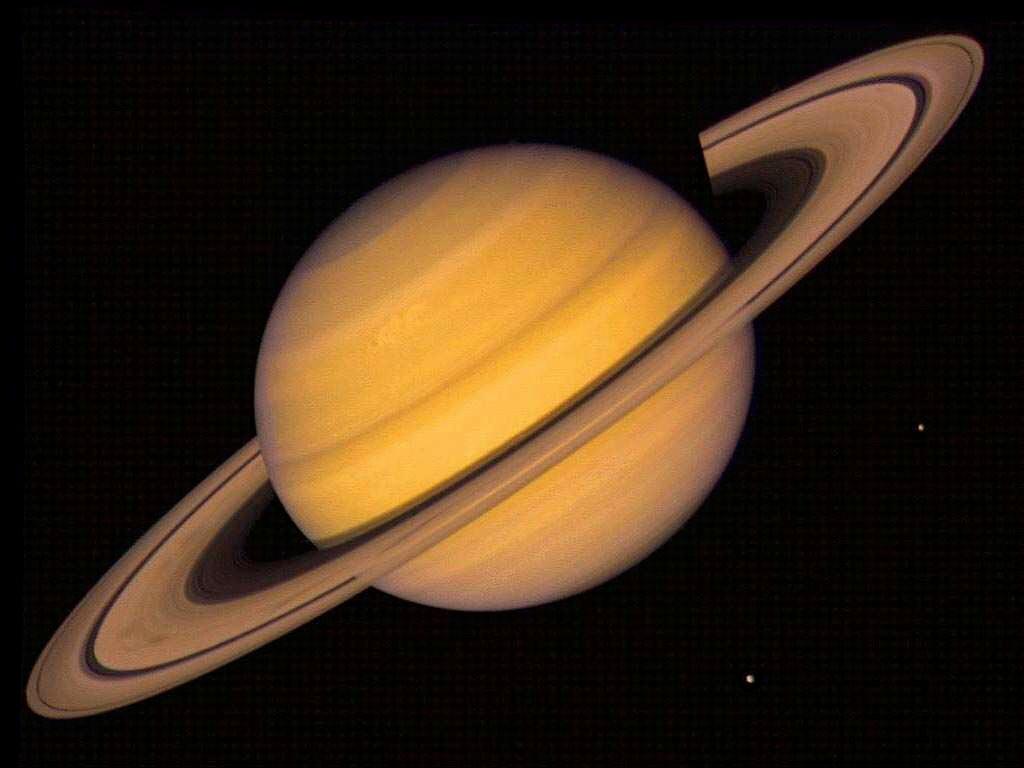
2.4 Геометрия в природе
Фигура, близкая к кругу, получится, если разрезать пополам апельсин, арбуз. Дугу можно увидеть после дождя на небе - радугу. Некоторые деревья, одуванчики, отдельные виды кактусов имеют сферическую форму. В природе многие ягоды имеют форму шара, например, смородина, крыжовник, черника. Двойной спиралью закручена молекула ДНК. Ураган закручивается по спирали, спирально плетёт свою паутину паук.
Другими интересными фигурами, которые мы можем повсеместно увидеть в природе, являются фракталы. Фракталы — это фигуры, составленные из частей, каждая из которых подобна целой фигуре.
Деревья, молния, бронхи и кровеносная система человека имеют фрактальную форму, идеальными природными иллюстрациями фракталов называют также папоротники и капусту брокколи. Трещины на камне: фрактал в макро.
Удар молнии — фрактальная ветка.
Замечали ли вы когда-нибудь растение, которое приковывает к себе взгляд своими правильными линиями, геометрическими формами, симметричным рисунком и другими внешними признаками. Например, Алоэ Polyphylla, Амазонская кувшинка, Крассула «Храм Будды», Цветок-калейдоскоп, Росолист лузитанский, Спиралевидный суккулент.


2.5 Геометрия у животных.
Принцип экономии хорошо «усвоили» животные. Сохраняя тепло, на холоде они спят, свернувшись в клубочек, поверхность тела уменьшается, и тепло лучше сохраняется. По этим же причинам северные народы строили круглые дома. Животные, конечно, же геометрию не изучали, но природа наделила их талантом строить себе дома в форме геометрических тел. Многие птицы — воробьи, крапивники, лирохвосты — строят свои гнёзда в форме полу шара. Есть архитекторы и среди рыб: в пресных водах живет удивительная рыба колюшка. В отличие от многих своих соплеменников она живет в гнезде, которое имеет форму шара. Но самые искусные геометры — пчёлы. Они строят соты из шестиугольников. Любая ячейка в сотах окружена шестью другими ячейками. А основание, или донышко, ячейки представляет собой трехгранную пирамиду. Такая форма выбрана неспроста. В правильный шестиугольник поместится больше меда, а зазоры между ячейками будут наименьшими! Разумная экономия усилий и строительных материалов.


2.6 Геометрия в транспорте.
По улице движутся автомобили, трамваи, троллейбусы. Их колеса с геометрической точки зрения – круги. В окружающем нас мире встречается много различных поверхностей, сложных по форме, не имеющих специальных названий. Паровой котел напоминает цилиндр. В нем находится пар под высоким давлением. Поэтому стенки цилиндра слегка (незаметно для глаза) изгибаются, образуя поверхность очень сложной и неправильной формы, которую инженеры должны знать, чтобы суметь правильно рассчитать котел на прочность. Сложную форму имеет и корпус подводной лодки. Он должен быть хорошо обтекаемым, прочным и вместительным. От формы корабельного корпуса зависит и прочность корабля, и его устойчивость и скорость. Результат работы инженеров над формой современных автомобилей, поездов, самолетов - высокие скорости движения. Если форма будет удачной, обтекаемой, сопротивление воздуха значительно уменьшается, за счет чего увеличивается скорость. Сложную форму имеют и детали машин – гайки, винты, зубчатые колеса и т.д. Рассмотрим ракеты и космические корабли. Корпус ракеты состоит из цилиндра (в котором находятся двигатель и горючее), а в конической головной части помещается кабина с приборами или с космонавтом

2.7 Геометрия в архитектуре.
Конечно, говорить о соответствии архитектурных форм геометрическим фигурам можно только приближенно, отвлекаясь от мелких деталей. В архитектуре используются почти все геометрические фигуры. Выбор использования той или иной фигуры в архитектурном сооружении зависит от множества факторов: эстетичного внешнего вида здания, его прочности, удобства в эксплуатации. Эстетические особенности архитектурных сооружений изменялись в ходе исторического процесса и воплощались в архитектурных стилях. Стилем принято называть совокупность основных черт и признаков архитектуры определенного времени и места. Геометрические формы, свойственные архитектурным сооружениям в целом и их отдельным элементам, также являются признаками архитектурных стилей.
Архитектура в наши дни имеет все более необычный характер. Здания становятся самых разных форм . Многие здания украшаются колоннами и лепнинами. Геометрические фигуры различной формы можно увидеть в постройке конструкциях мостов. Самые «молодые» здания- это небоскребы , подземные сооружения с модернизированным дизайном. Такие здания проектируются с использованием архитектурных пропорций.
Дом приблизительно имеет вид прямоугольного параллелепипеда. В современной архитектуре смело используются самые разные геометрические формы. Многие жилые дома, общественные здания украшаются колоннами.
Окружность как геометрическая фигура всегда привлекала к себе внимание художников, архитекторов. В неповторимом архитектурном облике Санкт-Петербурга восторг и удивление вызывает "чугунное кружево" - садовые ограды, перила мостов и набережных, балконные решетки и фонари. Четко просматриваемое на фоне фасада зданий летом, в изморози зимой, оно придает особое очарование городу. Особую воздушность придают воротам Таврического дворца (созданного в конце ХIII в. архитектором Ф.И. Волковым) окружности сплетенные в орнамент. Торжественность и устремленность ввысь - такой эффект в архитектуре зданий достигается использованием арок, представляющих дуги окружностей. Это видим на здании Главного штаба. (Санкт-Петербург). Архитектура православных церквей включает в себя как обязательные элементы купола, арки, округлые своды, что зрительно увеличивает пространство, создает эффект полета, легкости. А как красив Московский Кремль. Прекрасны его башни! Сколько интересных геометрических фигур положено в их основу! Например, Набатная башня. На высоком параллелепипеде стоит параллелепипед поменьше, с проемами для окон, а ещё выше воздвигнута четырехугольная усечённая пирамида. На ней расположены четыре арки, увенчанные восьмиугольной пирамидой. Геометрические фигуры различной формы можно узнать и в других замечательных сооружениях, возведенных русскими зодчими. Геометрическая форма сооружения настолько важна, что бывают случаи, когда в имени или названии здания закрепляются названия геометрических фигур. Так, здание военного ведомства США носит название Пентагон, что означает пятиугольник. Связано это с тем, что, если посмотреть на это здание с большой высоты, то оно действительно будет иметь вид пятиугольника. На самом деле только контуры этого здания представляют пятиугольник. Само же оно имеет форму многогранника.



3, Примеры геометрических тел
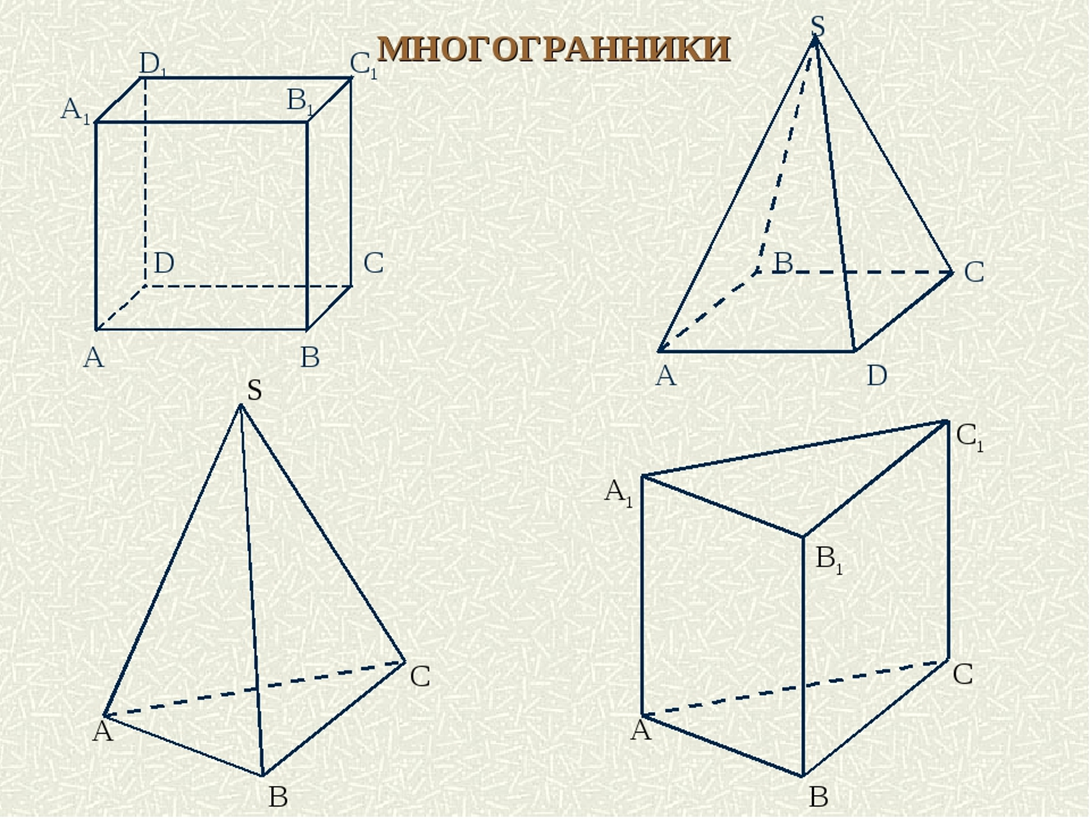
Куб — правильный многогранник, каждая грань которого представляет собой квадрат. Все ребра куба равны. Куб является частным случаем параллелепипеда и призмы.
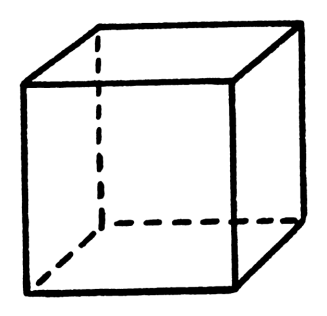
Развертка
Параллелепипед — многогранник, у которого шесть граней и каждая из них параллелограмм.
Прямоугольный параллелепипед — это параллелепипед, у которого все грани прямоугольники.
- трехмерный ( длина, ширина, высота)
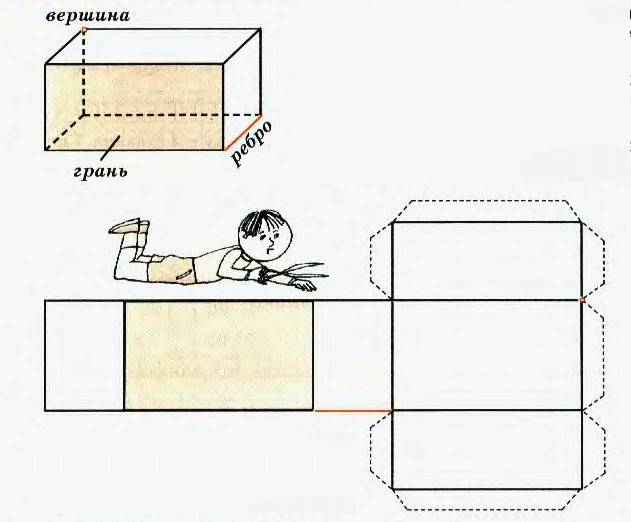
- призма четырехгранная

- наклонный параллелепипед (боковые грани которого не перпендикулярны основанию)

- ромбоэдр (грани которого – ромб)

Развертки

МАТЕРИАЛЫ И ИНСТРУМЕНТЫ
Бумага чертежная
Бумага ксероксная
Полистирол
Самоклеющаяся пленка
Скотч
Маркер
Ножницы
Линейка
Карандаш
ЭКОНОМИЧЕСКОЕ ОБОСНОВАНИЕ
| П.№ | Наименование | Ед.изм | Кол-во | Цена за ед.изм в рублях | Издержки |
| 1. | Бумага чертежная | Штук | 3 л | 45 | 5 |
| 2. | Ватман | Штук | 3 л | б/у | - |
| 3. | Полистирол | Штук | 5 л | б/у | - |
| 4. | Самоклеющаяся пленка | Метр | - | - | - |
| 5. | Скотч | Рулон | 1 | 10 | 2 |
| 6. | Маркер | Штук | 1 | 15 | - |
| 7. | Ножницы | Штук | 1 | - | - |
| 8. | Линейка | Штук | 1 | - | - |
| 9. | Карандаш | Штук | 1 | - | - |
ВЫВОД
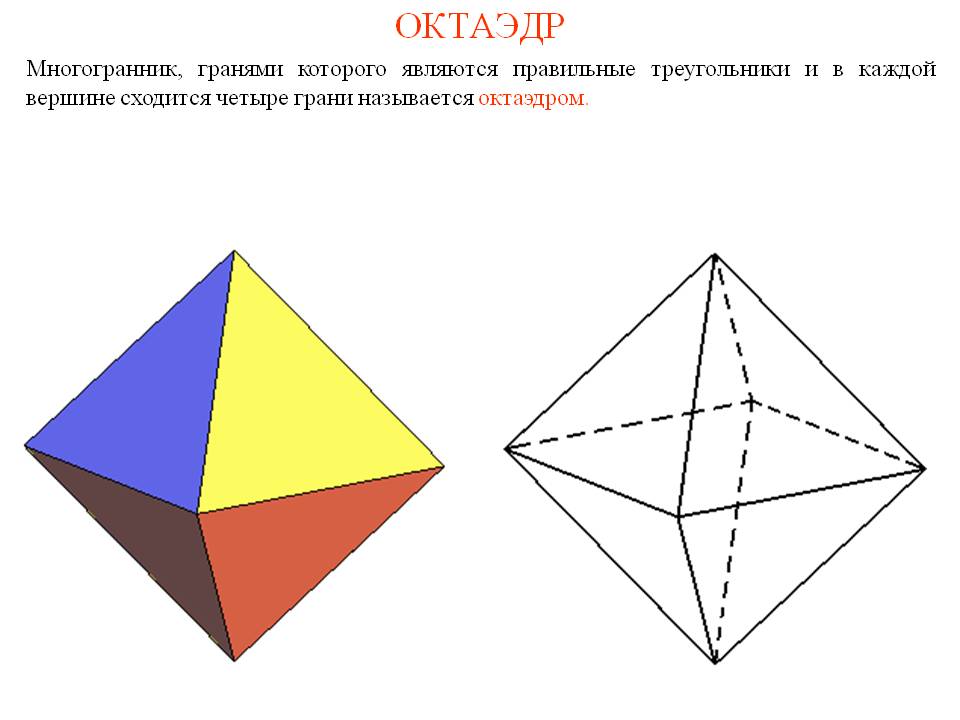
Создавая проект «Многогранники - геометрические тела», следует отметить, что до начала работы над темой, я не замечала или мало задумывалась о геометрии окружающего нас мира, Из всего сказанного делаю вывод, что геометрия в нашей жизни на каждом шагу и играет очень большую роль. Она нужна не только для того, чтобы называть части строений или формы окружающего нас мира. С помощью геометрии мы можем решить многие задачи, ответить на многие вопросы. я узнала, что такое многогранники : что куб и пирамида имеют другие названия –это тетраэдр и октаэдр . запомнила названия элементов фигур ,что они имеют ребра , грани и вершину.
На уроках геометрии , решая задачи по данной теме , мне стало более понятно как их решать ,находить вершину, ребра ,грани и т.д.
Еще я узнала , где применяются знания по геометрии, что эти знания очень важны при проектировании и строительстве любых сооружений . А так же в машиностроении и других науках.
СПИСОК ЛИТЕРАТУРЫ
Атанасян Л.С. «Геометрия» 10-11 класс /Москва «Просвещение» 2006г.
Преображенская Н.Г. «Черчение» 9 класс класс учебник для учащихся общеобразовательных учреждений .
Симоненко В.Д. « Технология» Учебник для учащихся 10 класса.
ИНТЕРНЕТ-РЕСУРСЫ
https://ru.wikipedia.org/
http://mathc.chat.ru/
www.5ballov.ru
http://www.nips.riss-telecom.ru/poly/
Мир многогранников
http://www.sch57.msk.ru:8101/collect/smogl.htm
ПРИЛОЖЕНИЕ
Чертеж-развертка правильной призмы –куб
Чертеж-развертка пирамиды – тетраэдра
Чертеж-развертка треугольной призмы, в основании прямоугольный равносторонний треугольник
Чертеж-развертка прямая треугольная призма
Чертеж-развертка четырехугольная призма
Эскизы многогранников
Правильные многогранники – это многогранники, у которого все грани являются правильными многоугольниками и все углы при вершинах равны.

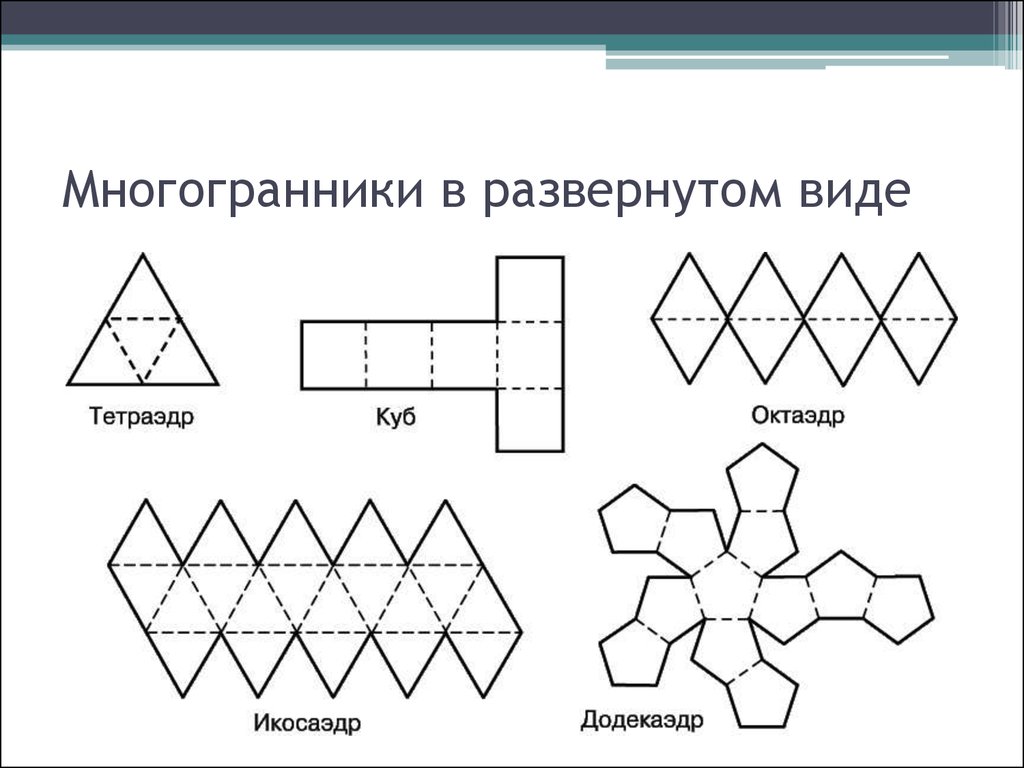
Вывод:
ГЕОМЕТРИЧЕСКИЕ ТЕЛА ВЫПОЛНЕННЫЕ ДЛЯ КАБИНЕТА МАТЕМАТИКИ
Правильная треугольная пирамида в сечении фигура -квадрат
Правильная треугольная пирамида в сечении- треугольник
Правильная четырехугольная призма- куб
Правильная треугольная пирамида - тетраэдр
Правильная наклонная призма в сечении –прямоугольник
Правильная прямая треугольная призма в основании -правильный треугольник
Правильная прямая четырехугольная призма - куб в сечении шестиугольник
Правильная прямая четырехугольная призма –куб вписан неправильный прямоугольник
Неправильная прямая четырехугольная призма в основании ромб
Прямая призма в основании прямоугольник , диагональ призмы наклонена к плоскости основания под углом 45 градусов
Прямая призма в основании ромб








































