Презентация "Многогранники. Вершины, ребра, грани многогранника. Теорема Эйлера."

Вершины, ребра, грани многогранника.Развертка Выпуклые многогранники.Теорема Эйлера.

Вопросы

1

Какие фигуры вы знаете в планиметрии?

2

Какие фигуры вы знаете в стереометрии?

3

Сколько вершин, ребер, граней у куба?

4

Сколько вершин, ребер, граней у тетраэдра?

5

Сколько вершин, ребер, граней у октаэдра?

Задача Эйлера

Задача. Три соседа имеют три общих колодца. Можно ли провести непересекающиеся дорожки от каждого дома к каждому колодцу?

В режиме слайдов ответы появляются после кликанья мышкой

То, что не получилось на рисунке, не является доказательством невозможности соединения дорожками домиков и колодцев. Для доказательства воспользуемся следующей теоремой Эйлера.

Теорема Эйлера

Теорема. Для связного простого графа имеет место равенство В - Р + Г = 2, где В - число вершин, Р - общее число ребер, Г - число областей (граней), на которые граф разбивает плоскость.

Доказательство . Стянем какое-нибудь ребро графа, соединяющее две вершины, в точку. При этом число ребер и число вершин уменьшаться на единицу и, следовательно, В – Р + Г не измениться. Продолжая стягивать ребра, мы придем к графу, у которого имеется одна вершина, а ребрами являются петли. Уберем какое-нибудь ребро. При этом число ребер и число областей уменьшаться на единицу и, следовательно, В – Р + Г не изменится. Продолжая убирать ребра, мы придем к графу, у которого имеется одна вершина и одно ребро. У этого графа В = 1, Р = 1, Г = 2 и, следовательно, В – Р + Г = 2. Значит, для исходного графа также выполняется равенство В – Р + Г = 2.

В режиме слайдов ответы появляются после кликанья мышкой

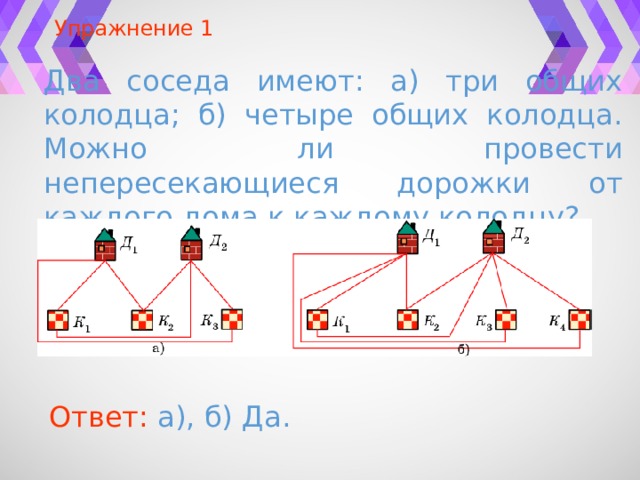
Упражнение 1

Два соседа имеют: а) три общих колодца; б) четыре общих колодца. Можно ли провести непересекающиеся дорожки от каждого дома к каждому колодцу?

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: а), б) Да.

Упражнение 2

Три соседа имеют: а) два общих колодца; б) четыре общих колодца. Можно ли провести непересекающиеся дорожки от каждого дома к каждому колодцу?

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: а) Да; б) нет.

Практическая работа №1 МНОГОГРАННИКИ

• 1. Начертите полученные фигуры
• 2. Посчитайте у каждой фигуры число вершин, ребер, граней.
• 3. Для каждой фигуры проверьте теорему Эйлера.

В+Г-Р=2 Запишите теорему Эйлера. (стр. 63)

• 4. Начертите развертку своих фигур.
• 5. Сделайте вывод .

РАзвертка

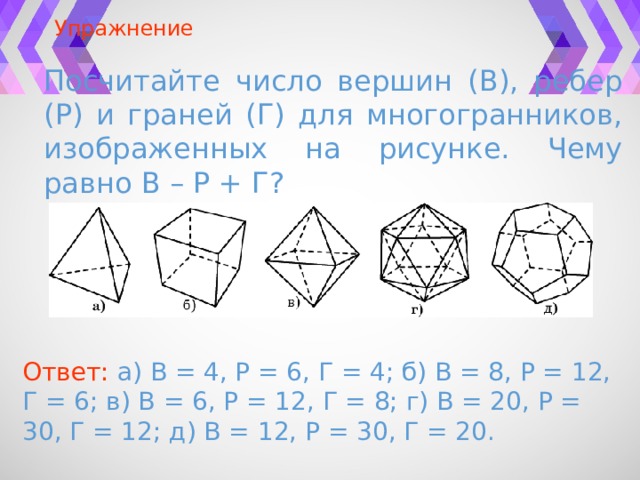
Упражнение

Посчитайте число вершин (В), ребер (Р) и граней (Г) для многогранников, изображенных на рисунке. Чему равно В – Р + Г?

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: а) В = 4, Р = 6, Г = 4; б) В = 8, Р = 12, Г = 6; в) В = 6, Р = 12, Г = 8; г) В = 20, Р = 30, Г = 12; д) В = 12, Р = 30, Г = 20.