Тема урока: Множества и операции над ними.
Учитель Рыкова Л.Г.
Цели урока:
-
образовательные: повторить основные понятия множества, подмножества, операции над множествами;
-
развивающие: развитие логического мышления через решение нестандартных задач, систематизацию и обобщение, развитие математической речи,
-
воспитательные: воспитание внимательности, интереса к предмету, расширение кругозора, воспитывать грамотную математическую речь.
-
Тип урока: комбинированный урок - изучение и первичное осознание нового учебного материала, осмысление связей и отношений в объектах изучения, совершенствование вычислительных навыков.
-
Формы работы учащихся: фронтальная работа, групповая технология, ИКТ.
-
Необходимое техническое оборудование: компьютер, мультимедийный проектор, доска, экран
Ход урока:
I этап. Сообщение темы, цели, задач урока и мотивация учебной деятельности.
Одним из основных понятий математики является понятие множества, и, как каждое основное понятие, не поддаётся точному определению (например, понятия “точка”, “прямая” являются одними из основных понятий геометрии).
«Множество есть многое, мыслимое нами как единое» ( Г. Кантор)
(слайд 2)
Историческая справка 1 (сообщение обучающихся)
Понятие множество связано с таким известным в математике именем как Кантор (Cantor) Георг (1845—1918) — немецкий математик, логик, теолог, создатель теории трансфинитных (бесконечных) множеств, оказавшей определяющее влияние на развитие математических наук на рубеже 19— 20 вв. В семидесятые годы ХIX века немецкий математик Георг Кантор, исследуя тригонометрические ряды и числовые последовательности, встал перед необходимостью сравнить между собой бесконечные совокупности чисел. Для решения возникших при этом проблем Кантор и выдвинул понятие множества. Это понятие, введенное в достаточно узкой области математики для довольно специальных целей, вскоре стало с успехом применяться в других ее областях. Посвященные ему исследования приобрели самостоятельный интерес и выделились в особый раздел математики – теорию множеств.
Теория множеств появилась на свет 7 декабря 1873 года.
Кантора заинтересовал вопрос, каких чисел больше – натуральных или действительных?
В одном из писем адресованных к своему приятелю Рихарду Дедекинду, Кантор писал, что ему удалось доказать посредством множеств, что действительных чисел больше, чем натуральных. День, которым было датировано это письмо, математики считают днем рождения теории множеств.
(слайд 3,4)
II этап. Проверка домашнего задания, уточнение направлений актуализации изученного материала.
Учитель. - Множество - одно из основных понятий современной математики, используемое почти во всех её разделах. К сожалению, основному понятию теории – понятию множества – нельзя дать строгого определения. МНОЖЕСТВОМ называется собрание, совокупность объектов, объединенных по какому-нибудь общему признаку, свойству. Понятие множества поясняется при помощи примеров: множество книг на полке, множество точек на прямой (точечное множество) и т. д.. Множества обозначаются прописными (заглавными) буквами латинского алфавита (без индексов или с индексами). Например: B, C, … , X, Y, … ,A1,B1, …
Математический смысл слова “множество” отличается от того, как оно используется в обычной речи. Так, в обычной речи понятие “множество” связывают с большим числом предметов, в математике же этого не требуется. Здесь могут рассматриваться множества, содержащие один объект, много объектов, несколько объектов или не содержащие ни одного объекта.
Объекты, из которых состоит множество, называются его ЭЛЕМЕНТАМИ. Элементы множества обозначаются строчными (малыми) буквами латинского алфавита. Например: b,c, … , x, y, … , a1, b1, … Если элемент х принадлежит множеству М, то записывают х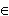 М, если не принадлежит – x
М, если не принадлежит – x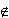 M.
M.
Множества можно задать, перечислив все его элементы или указав характеристическое свойство элементов, т.е. такого свойства, которым обладает любой элемент данного множества и не обладает ни один элемент, не принадлежащий ему.
Примеры множеств:
-
множество дней недели;
-
множество планет солнечной системы;
-
множество месяцев;
-
множество знаков зодиака;
-
числовые множества.
Приведите свой пример множества.
ТЕОРЕТИЧЕСКАЯ РАЗМИНКА:
(слайд 5- 12)
-
1. Что означает слово «множество»? (Множество – это набор или совокупность предметов одинаковой природы).
-
2. Как различаются множества по числу элементов? (Множества бывают конечные, бесконечные и пустое множество).
-
4. Какими способами можно задать множество? (Множество можно задать перечислением, с помощью характеристического свойства, графически).
-
5. Какое свойство называется характеристическим свойством? (Характеристическим свойством называется такое свойство, которым обладают все элементы данного множества и не обладают никакие другие объекты).
(Слайд 13-17)
-
Леонард Эйлер (1707-1783) – швейцарский, немецкий и российский математик и механик, внесший огромный вклад в развитие этих наук.
-
Жизнь Леонарда Эйлера была полна удивительных открытий, принесших человечеству огромную пользу. Его масштабный вклад в развитие математики, механики, физики и астрономии невозможно переоценить, а его познания в самых разнообразных отраслях науки вызывают восхищение. За всю свою жизнь он издал более 850 трудов, в которых содержатся глубокие исследования ботаники, химии, медицины, древних языков. Имел членство во многих Академиях наук по всему миру.
-
Круги Эйлера — это геометрическая схема, которую можно применять для наглядного отображения отношений между множествами. Диаграммы разработал известный математик и механик, чьим именем и назван метод. Учёный считал, что его подход облегчает размышления человека.
Какие операции можно выполнять над множествами? (объединение, пересечение, вычитание).
III этап. Изучение нового материала.
Повторение.
(Слайды 17, 18)
-
Два множества А и В называются равными ( А = В ), если они состоят из одних и тех же элементов, то есть каждый элемент множества А является элементом множества В и наоборот, каждый элемент множества В является элементом множества А.
-
Если каждый элемент множества А является элементом множества В, то множество А называется подмножеством В. Обозначение: А Ì В. Знак « Ì » - знак включения.
Рассмотрим некоторые операции над множествами.
(Слайды 20- 23)
Какие операции можно выполнять над множествами? (объединение, пересечение, вычитание).
Объединением двух множеств А и В называется такое множество С, которое состоит из всех тех элементов, которые принадлежат хотя бы одному из множеств А или В.
Символически объединение двух множеств А и В обозначается так:
А В, где - символ объединения множеств. Определение можно записать с помощью характеристического свойства:
С = А В={x xA или xB}.
(Слайды 21)
Пересечением множеств А и В называется множество, состоящее их всех тех и только тех элементов, которые принадлежат множествам А и В одновременно.
Символически пересечение множеств А и В обозначается так: АВ, где символ - знак пересечения множеств. Используя характеристическое свойство, определение можно записать следующим образом:
Р = А В= {x xA и xB}.
(Слайд 22)
Вычитание множеств.
Разностью множеств А и В называется множество, содержащее те и только те элементы, которые принадлежат множеству А и не принадлежат множеству В.
А\В={х|х Є А и х ∉ В}
(Слайд 23)
IV этап. Воспроизведение изученного и его применение в стандартных условиях.
(Слайд 24)
УПРАЖНЕНИЕ № 1. (Слайд 25)
Множество задано путем перечисления своих элементов. Придумайте какое-нибудь его словесное описание.
-
{0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
-
{A, B, C, D, E, … X, Y, Z};
-
{0, 2, 4, 6, 8}.
УПРАЖНЕНИЕ № 2. (Слайд 26)
Даны множества:
А = {2, 5, 0, 11, 12, 19}, В = {2, 7, 8, 12, 13, 9, 0}.
Найдите множества A Ç В, А È В, А\В, В\А.
Ответы:
-
A В= {2, 0, 12},
-
А В= {2, 5, 0, 11, 12, 19, 7, 8, 13, 9},
-
А\В = { 5, 11, 19},
-
В\А = { 7, 8, 13, 9}.
УПРАЖНЕНИЕ № 3. (Слайд 27)
-
Задайте множество груш, растущих на берёзе.
-
Задайте множество чисел, которые делятся на 0.
УПРАЖНЕНИЕ № 4. (Слайд 28)
Даны множества: М = {5, 4, 6}, Р = {4, 5, 6}, Т = {5, 6, 7}, S = {4, 6}. Какое из утверждений неверно?
а) М = Р. б) Р ≠ S. в) М ≠ Т. г) Р = Т.
УПРАЖНЕНИЕ № 5. (Слайд 29)
-
Среди перечисленных ниже множеств укажите конечные и бесконечные множества:
-
а) множество чисел, кратных 11;
б) множество делителей числа 5;
в) множество океанов;
г) множество натуральных чисел;
д) множество рек России;
е) множество корней уравнения х - 3 = 10.
УПРАЖНЕНИЕ № 6. (Слайд 30)
-
Даны множества:
-
А – множество фруктов в корзине;
В – множество яблок в этой корзине;
С – множество груш в этой корзине;
Д – множество слив в этой корзине.
-
Чем являются множества В, С и Д для множества А?
УПРАЖНЕНИЕ № 7. (Слайд 31 -35)
Изобразите с помощью кругов Эйлера пересечение множеств A и В, если: а) А Ç В; б) А È В; в) А = В; г) А Ç В = ᴓ .
УПРАЖНЕНИЕ № 8 (Слайд 36)
Расположите 4 элемента a, b, c, d в двух множествах так, чтобы в каждом из них было по 3 элемента.
УПРАЖНЕНИЕ № 9 (Слайд 37)
Множества А и В содержат соответственно 5 и 6 элементов, а множество А ∩ В – 2 элемента. Сколько элементов в множестве А U В?
V этап. Перенос приобретенных знаний и их первичное применение в новых или измененных условиях с целью формирования умений.
ЗАДАЧА 1 (Слайд 38)
Каждый учащийся в классе изучает английский или французский язык. Английский язык изучают 25 учащихся, французский — 27 учащихся, а два языка — 18 учащихся. Сколько учащихся в классе?
ЗАДАЧА 2 (Слайд 39)
Каждая семья, живущая в нашем доме, выписывает или
газету, или журнал, или и то и другое вместе. 75 семей
выписывают газету, а 27 семей выписывают журнал и лишь 13 семей выписывают и журнал, и газету. Сколько семей живет в нашем доме?
Ответить на вопросы теста:
Тест по теме «Множества»
1. Определить какое из множеств является подмножеством
А = {5, 15, 25, 35, 45, 55}
a) {55} б) {5, 25, 50} в) {25, 55, 75}
2. Какое из множеств определяет 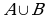 , если А = {2, 4, 6, 8, 10}, B = {8, 10, 12, 14}
, если А = {2, 4, 6, 8, 10}, B = {8, 10, 12, 14}
a) {2, 4, 6, 8, 10, 12, 14} б) {8, 10, 12, 14} в) {8, 10}
3. Какое из множеств определяет 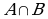 , если A = {2, 4, 6, 8, 10}, B = {2, 4, 8, 9}
, если A = {2, 4, 6, 8, 10}, B = {2, 4, 8, 9}
а) {2, 4, 6, 8, 10} б) {2, 4, 8, 9} в) {2, 4, 8}
4. На каком рисунке изображено пересечение множеств А и В (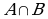 )?
)?
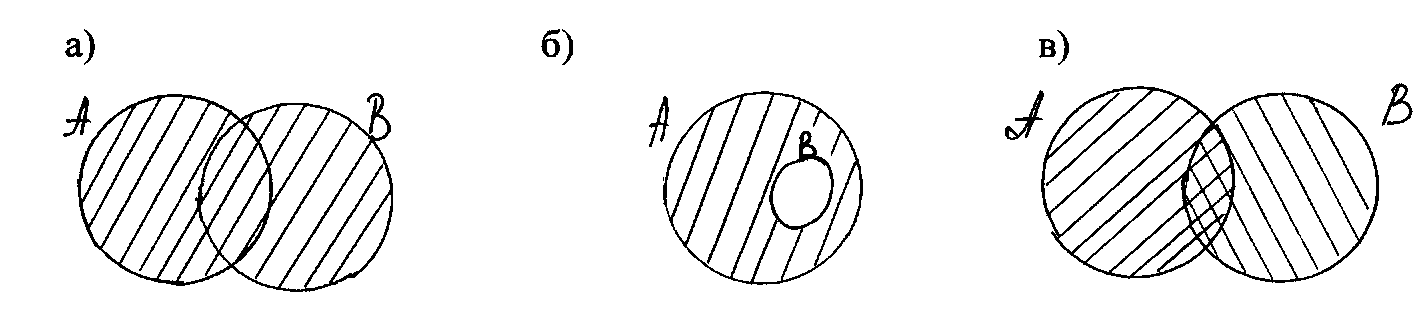
-
Сообщение на тему «Фракталы». (Слайды 45-54)
-
Фрактал (лат. fractus — дробленый) — термин, означающий геометрическую фигуру, обладающую свойством самоподобия, то есть составленную из нескольких частей, каждая из которых подобна всей фигуре целиком.
-
Множество, обладающее свойством самоподобия. В математике под фракталами понимают множества точек в евклидовом пространстве, имеющие дробную метрическую размерность.
VI этап. Рефлексия. Подведение итогов урока.
Продолжите слова:
сегодня я узнал… теперь я могу… я научился… было интересно…
меня удивило… я приобрел… мне захотелось…
VII этап. Постановка задания на дом. (Слайды 55-58)
ТЕСТ.
Тест по теме «Множества»
Тест с выбором правильного ответа.
ИНСТРУКЦИЯ: Выберите букву с правильным ответом и занесите её в бланк ответов.
1. Определить какое из множеств является подмножеством А = {10, 20, 30, 40, 50, 60}
a) {10, 20, 30, 40, 50, 60, 70} б) {10} в) {10, 35}
2. Какое из множеств определяет 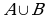 , если А = {1, 2, 3, 4, 5}, B = {3, 4, 5, 6, 7}
, если А = {1, 2, 3, 4, 5}, B = {3, 4, 5, 6, 7}
a) {1, 4, 5} б) {1, 2, 3, 4, 5} в) {1, 2, 3, 4, 5, 6, 7}
3. Какое из множеств определяет 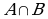 , если A = {1, 3, 5, 7, 9}, B={1, 2, 3, 4}
, если A = {1, 3, 5, 7, 9}, B={1, 2, 3, 4}
а) {1, 3, 5, 7} б) {1, 2, 3, 4, 5, 7, 9} в) {1, 3}
4. На каком рисунке изображено объединение множеств А и В (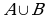 )?
)?

Задача для любознательных (Слайд 40)
-
Многие ребята нашего класса любят футбол, баскетбол и волейбол. А некоторые - даже два или три из этих видов спорта. Известно, что 6 человек из класса играют только в волейбол, 2 – только в футбол, 5 – только в баскетбол. Только в волейбол и футбол умеют играть 3 человека, в футбол и баскетбол – 4, в волейбол и баскетбол – 2. Один человек из класса умеет играть во все игры, 7 не умеют играть ни в одну игру. Требуется найти:
-
Сколько всего человек в классе?
-
Сколько человек умеют играть в футбол?
-
Сколько человек умеют играть в волейбол?
9







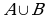 , если А = {2, 4, 6, 8, 10}, B = {8, 10, 12, 14}
, если А = {2, 4, 6, 8, 10}, B = {8, 10, 12, 14}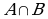 , если A = {2, 4, 6, 8, 10}, B = {2, 4, 8, 9}
, если A = {2, 4, 6, 8, 10}, B = {2, 4, 8, 9}



















