МОЙ МЕТОД РАЗРАБОТКИ

Метод Координат

Геометрия9 класс

30 октября 1888 года

Американский «самоделкин» Джон Лауд получил патент на «авторучку с вращающимся наконечником» — небольшим шариком на конце полого стержня, заполненного чернилами.

Мало иметь

хороший ум,

главное - хорошо его применять.

Кроссворд

2

3

4

5

1

6

Кроссворд

3

2

С

Т

О

Р

Е

Н

5

У

4

А

Г

К

О

П

О

Р

Р

О

А

Л

Т

Л

1

В

Ь

Л

О

О

Н

И

Г

Л

Д

О

Н

Е

И

И

Е

Н

К

Н

Н

А

А

А

Н

Р

Ы

Л

6

Е

Ь

Н

Т

О

Н

Ы

Ч

Ы

Е

К

Е

А

Рене Декарт (1596 -1650)

Французский математик, физик, физиолог и философ, создатель знаменитого метода координат, сторонник аналитического метода в математике.

Впервые прямоугольную систему координат он ввел в своей работе «Рассуждение о методе» в 1637 году. Поэтому прямоугольную систему координат называют также — Декартова система координат .

Историческое значение Декартовой геометрии :

применение алгебраических методов к геометрическим объектам.

Введение системы прямолинейных координат означало создание аналитической геометрии, объединяющей геометрические и арифметические величины, которые со времен древнегреческой математики существовали в раздельности.

"Я мыслю, следовательно, я существую"

Блиц-опрос

Уравнение прямой

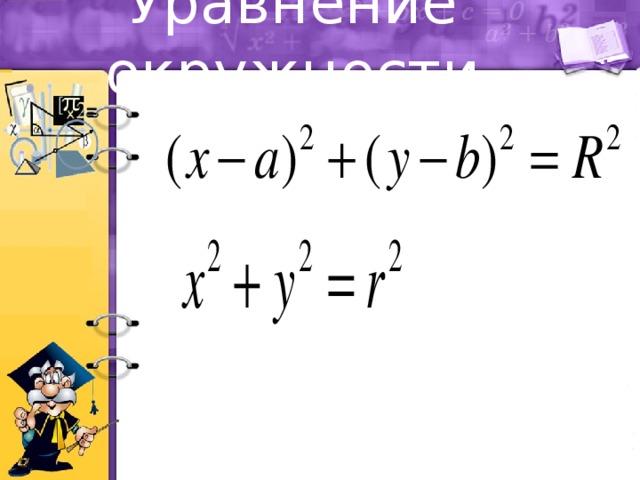
Уравнение окружности

Взаимное расположение прямых на плоскости

параллельны

совпадают

перпендикулярны

пересекаются

Математический турнир

• Найдите длину отрезка.
• Найдите координаты середины отрезка.
• Найдите координаты вектора .
• Составьте уравнение окружности.
• Определите взаимное расположение прямых.

Электронная

физминутка

для глаз

Решение задач

Треугольник АВС ограничен прямыми, заданными уравнениями

3х+4y-24=0, x=0, y=0.

• Определите координаты вершин треугольника.
• Окружность с центром в точке К и радиусом r вписана в треугольник АВС. Составьте уравнение этой окружности.
• Окружность с центром в точке М описана около треугольника АВС. Составьте уравнение этой окружности.
• Составьте уравнение прямой КМ.
• Параллельны ли прямые КВ и МР, если Р(1; 4)?
• Составьте уравнение прямой, параллельной оси ОУ и проходящей через точку М.
• При каких значениях параметра m прямая у = 2m будет касательной к окружности К(r)?

Решение задач

Используя метод координат, решите систему уравнений:

Решение:

ГИА

Решение задач

Составить уравнение прямой, параллельной прямой y = 2x + 3 и проходящей через точку (1; 7).

Решение:

Уравнения параллельных прямых имеют одинаковые угловые коэффициенты, то уравнение каждой прямой, параллельной прямой y = 2x + 3, может быть записано в виде y = 2x + d , где d ─ некоторое число.

Параллельная прямая проходит через точку (1; 7)

7 = 2 *1+ d d = 5

y = 2x + 5

ЕГЭ

Решение задач

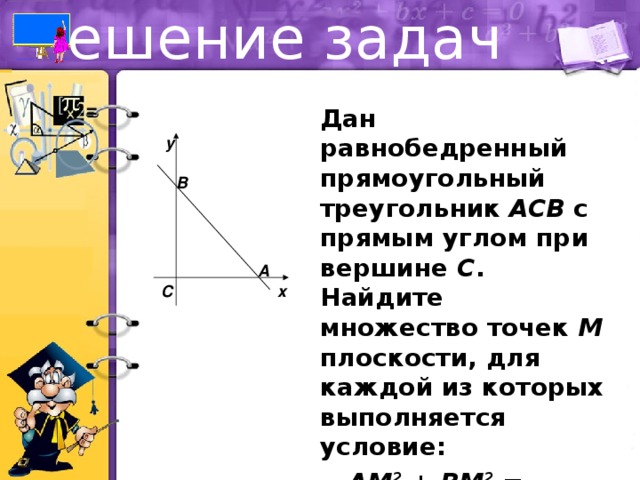
Дан равнобедренный прямоугольный треугольник ACB с прямым углом при вершине C . Найдите множество точек M плоскости, для каждой из которых выполняется условие:

AM 2 + BM 2 = 2CM 2 .

y

B

A

x

C

Решение задач

Если катет данного треугольника равен a , тогда С ( 0; 0 ) , А ( a; 0 ) , В ( 0; a ) . Пусть ( x; y ) – координаты точки M , принадлежащей искомому множеству точек.

Воспользуемся формулой для нахождения расстояния между точками, если известны их координаты:

По условию задачи AM 2 + BM 2 = 2CM 2 , следовательно,

( x – a ) 2 + y 2 + x 2 + ( y – a ) 2 = 2 ( x 2 + y 2 ) .

x + y – a = 0 .

Если точка M ( x; y ) не принадлежит искомому

множеству точек, то AM 2 + BM 2 ≠ 2CM 2 , а

значит, координаты точки M не удовлетворяют

уравнению x + y – a = 0 .

Таким образом, x + y – a = 0 есть уравнение

искомого множества точек и это множество есть прямая,

на которой лежит гипотенуза AB данного треугольника.

y

B

A

x

C

Домашнее задание

Домашнее задание

( разноуровневое )

Рефлексия учащихся.

• сегодня я узнал…
• было интересно…
• было трудно…
• я научился…
• у меня получилось …
• я попробую…
• меня удивило…

Итог урока

«… потомки будут благодарны мне не только за то, что я сказал, но и за то, что я не сказал и тем самым дал им возможность и удовольствие додуматься до этого самостоятельно»

Рене Декарт

Цветы для ВАС!

Спасибо вам за успешную работу на уроке, а нашим гостям – за внимание!

вам за успешную работу на уроке, а нашим гостям – за внимание!

вам за успешную работу на уроке, а нашим гостям – за внимание!